Wavelet analysis of density fluctuation in supersonic turbulent boundary layer

Zhang Bo; He Lin; Yi Shi-He

doi:10.7498/aps.69.20200748

Abstract

In order to obtain the time-varying information and dynamic characteristics of density fluctuation in compressible turbulence, the wavelet method is used to analyze the flow density field of zero-pressure-gradient flat plate turbulent boundary layer at Ma = 3.0, which is measured based on Nano-tracer plane laser scattering technique. Utilizing Taylor’s frozen hypothesis, the spatial signal of density field converts into the temporal signal. The one-dimensional orthogonal wavelet multi-resolution analysis is used to reveal multi-scale turbulent structures, and the results suggest that large-scale structures play a leading role in the density fluctuation of turbulent boundary layer while the small-scale structures make the probability density function (PDF) of density fluctuation manifested as an “M” distribution. The density fluctuation scalar PDF deviates from Gaussian distribution. The Hilbert transformation is used to analyze amplitude modulation effects between large- and small-scale structure, and the results suggest that positive (negative) large scale density excursion in the outer layer induces local enhancement (suppression) of the small scale density fluctuation in the inner layer near the wall. The time-varying spectral density estimation method based on the wavelet transform is used to analyze the density fluctuation at different heights of turbulent boundary layer after proving its viability in time and frequency domain. The results suggest a wide range of frequencies throughout the turbulent boundary layer, mainly distributed within 1 MHz. The density fluctuation in the dominant frequency band is intermittent, most of which transits from high frequency to low frequency while the spectral density first increases and then decreases. Near the wall, the time-frequency distributions of density fluctuation in the logarithmic layer are similar. In the middle part of the turbulent boundary layer, the frequency distribution and spectral density of the density fluctuation each reach a peak. Near the mainstream region, the spectral density decreases obviously, which is mainly distributed near the structure formed by the interaction between the boundary layer and mainstream. The wall constraint, viscous dissipation, and uniform mainstream make the fluctuation nearby the region relatively weak. As a result, the spectrum amplitude of density fluctuation first increases and then decreases from the wall to the mainstream.

Keywords:

Authors and contacts

College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China

Corresponding author: He Lin, helin_nudt@foxmail.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 91752102) and the Excellent Innovation Young Project of Changsha, China (Grant No. KQ1802031)

FullText HTML : translate this paragraph

References

[1]	Lee C B, Jiang X Y 2019 Phys. Fluids 31 111301 Google Scholar
[2]	Pan L B, Padoan P, Nordlund A 2018 Astrophys. J. Lett. 866 L17 Google Scholar
[3]	Pan L B, Padoan P, Nordlund A 2019 Astrophys. J. 881 155 Google Scholar
[4]	王正魁, 靳旭红, 朱志斌, 程晓丽 2018 航空学报 39 122244 Google Scholar Wang Z K, Jin X H, Zhu Z B, Cheng X L 2018 Acta Aeronaut. Astronaut. Sin. 39 122244 Google Scholar
[5]	Tian Y F, Jaberi F A, Livescu D 2019 J. Fluid Mech. 880 935 Google Scholar
[6]	Parziale N, Shepherd J, Hornung H 2015 J. Fluid Mech. 781 87 Google Scholar
[7]	He L, Yi S H, Zhao Y X, Tian L F, Chen Z 2011 Chin. Sci. Bull. 56 489 Google Scholar
[8]	何霖, 易仕和, 陆小革 2017 66 024701 Google Scholar He L, Yi S H, Lu X G 2017 Acta Phys. Sin. 66 024701 Google Scholar
[9]	Tian L F, Yi S H, Zhao Y X, He L, Cheng Z Y 2009 Sci. China, Ser. G 52 1357 Google Scholar
[10]	Morkovin M V 1962 Mécanique de la Turbulence 367 380
[11]	Berkooz G, Holmes P, Lumley J L 1993 Annu. Rev. Fluid Mech. 25 539 Google Scholar
[12]	Smith T R, Moehlis J, Holmes P 2005 Nonlinear Dyn. 41 275 Google Scholar
[13]	Schmid P J 2010 J. Fluid Mech. 656 5 Google Scholar
[14]	Schmid P J, Li L, Juniper M P, Pust O 2011 Theor. Comput. Fluid Dyn. 25 249 Google Scholar
[15]	Ruppert-Felsot J, Farge M, Petitjeans P 2009 J. Fluid Mech. 636 427 Google Scholar
[16]	赵玉新, 易仕和, 田立丰, 何霖, 程忠宇 2010 中国科学: 计算科学 53 584 Google Scholar Zhao Y X, Yi S H, Tian L F, He L, Cheng Z Y 2010 Sci. China Ser. E: Technol. Sci. 53 584 Google Scholar
[17]	Rinoshika A, Omori H 2011 Exp. Therm. Fluid Sci. 35 1231 Google Scholar
[18]	Zheng X B, Jiang N 2015 Chin. Phys. B 24 064702 Google Scholar
[19]	Freund A, Ferrante A 2019 J. Fluid Mech. 875 914 Google Scholar
[20]	赵玉新, 易仕和, 何霖, 田立丰 2010 科学通报 55 2004 Google Scholar Zhao Y X, Yi S H, Tian L F, He L, Cheng Z Y 2010 Chin. Sci. Bull. 55 2004 Google Scholar
[21]	Chen Z, Yi S H, He L, Zhu Y Z, Ge Y, Wu Y 2014 J. Visualization 17 345 Google Scholar
[22]	Liu X L, Yi S h, Xu X W, Shi Y, Ouyang T C, Xiong H X 2019 Phys. Fluids 31 074108 Google Scholar
[23]	He L, Yi S H, Zhao Y X, Tian L F, Chen Z 2011 Sci. China, Ser. G 54 1702 Google Scholar
[24]	Taylor G I 1938 Proc. R. Soc. London, Ser. A 164 476 Google Scholar
[25]	Rinoshika A, Zhou Y 2005 J. Fluid Mech. 524 229 Google Scholar
[26]	Van Doorne C, Westerweel J 2007 Exp. Fluids 42 259 Google Scholar
[27]	Ganapathisubramani B, Lakshminarasimhan K, Clemens N T 2007 Exp. Fluids 42 923 Google Scholar
[28]	Vétel J, Garon A, Pelletier D 2010 Exp. Fluids 48 441 Google Scholar
[29]	曹晖, 赖明, 白绍良 2004 工程力学 21 109 Google Scholar Cao H, Lai M, Bai S L 2004 Eng. Mech. 21 109 Google Scholar
[30]	Spanos P D, Failla G 2004 J. Eng. Mech. 130 952 Google Scholar
[31]	Mouri H, Kubotani H, Fujitani T, Niino H, Takaoka M 1999 J. Fluid Mech. 389 229 Google Scholar
[32]	Mallat S G 1989 IEEE Trans. Pattern Anal. Mach. Intell. 11 674 Google Scholar
[33]	Rinoshika A, Watanabe S 2010 Exp. Therm. Fluid Sci. 34 1389 Google Scholar
[34]	Hutchins N, Marusic I 2007 Philos. Trans. R. Soc. London, Ser. A 365 647 Google Scholar
[35]	Mathis R, Hutchins N, Marusic I 2009 J. Fluid Mech. 628 311 Google Scholar
[36]	Mathis R, Monty J P, Hutchins N, Marusic I 2009 Phys. Fluids 21 111703 Google Scholar
[37]	He G S, Pan C, Feng L H, Gao Q, Wang J J 2016 J. Fluid Mech. 792 274 Google Scholar
[38]	He G S, Wang J J, Rinoshika A 2019 Phys. Rev. E 99 053105 Google Scholar
[39]	Gurley K, Kareem A 1999 Eng. Struct. 21 149 Google Scholar
[40]	白泉, 边晶梅, 康玉梅 2018 小波理论在工程结构振动分析中的应用 (北京: 清华大学出版社) 第32−49页 Bai Q, Bian J M, Kang Y M 2018 Application of Wavelet Theory in Vibration Analysis of Engineering structures (Beijing: Tsinghua Univesity Press) pp32−49 (in Chinese)
[41]	何霖 2011 博士学位论文 (长沙: 国防科学技术大学) He L 2011 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[42]	Eswaran V, Pope S 1988 Phys. Fluids 31 506 Google Scholar
[43]	Antonia R A, Mi J 1993 J. Fluid Mech. 250 531 Google Scholar

Cited By

图 1 Meyer小波频域定义与时域波形

Figure 1. Meyer wavelet in frequency and time domain.

DownLoad: Full-Size Img PowerPoint

图 2 时频域有效性验证　(a) 密度脉动累积能量曲线; (b) 密度脉动功率谱估计

Figure 2. Verification in time and frequency domain: (a) Husid of density wave; (b) power spectral density (PSD) of density fluctuation.

DownLoad: Full-Size Img PowerPoint

图 3 $Ma$ = 3.0湍流边界层流向剖面　(a) 瞬态密度场; (b) 瞬态密度脉动

Figure 3. Flow profile of turbulent boundary layer at $Ma$ = 3.0: (a) Instantaneous density field; (b) instantaneous density fluctuation.

DownLoad: Full-Size Img PowerPoint

图 4 密度脉动时间分布曲线($y/\delta $ = 0.1)

Figure 4. Time distribution curve of density fluctuation ($y/\delta $ = 0.1).

DownLoad: Full-Size Img PowerPoint

图 5 密度脉动信号多分辨率分析　(a)−(f) Level 1−Level 6代表组成原始信号6个不同尺度的分量

Figure 5. Multiresolution analysis of density fluctuation signal: (a)−(f) Level 1−Level 6 represent 6 different sacles’s components of original signal.

DownLoad: Full-Size Img PowerPoint

图 6 原始信号和Level 1 + Level 2的概率密度函数

Figure 6. Probability density function (PDF) of the original signal of density fluctuation and Level 1 + Level 2.

DownLoad: Full-Size Img PowerPoint

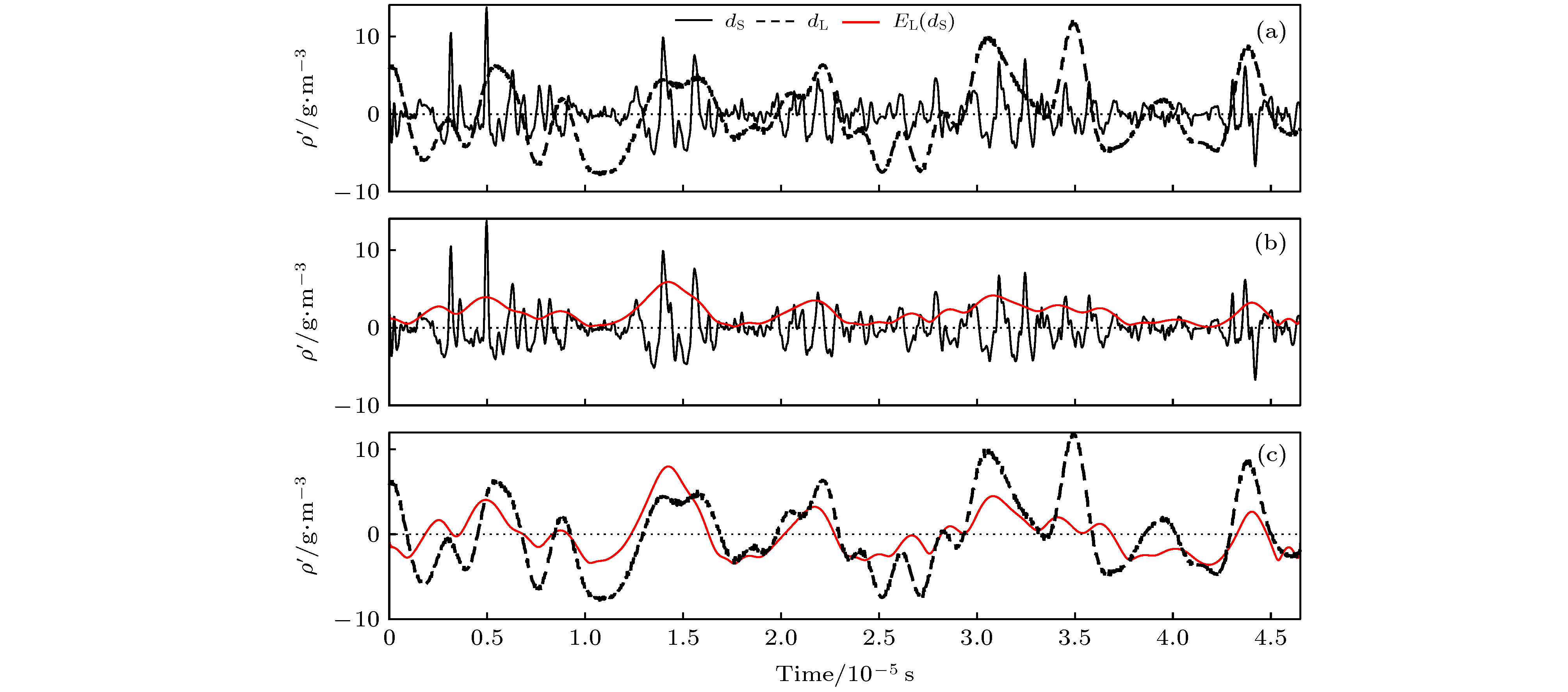
图 7 幅度调制效应分析　(a) 大尺度分量${d_{\rm{L}}}$与小尺度分量${d_{\rm{S}}}$; (b) 小尺度分量${d_{\rm{S}}}$与低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$; (c) 大尺度分量${d_{\rm{L}}}$与低通滤波包络${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$(为方便比较, 将${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$平均值调整到0线并放大2倍)

Figure 7. Analysis of amplitude modulation effects: (a) Large scale component ${d_{\rm{L}}}$ and small scale component ${d_{\rm{S}}}$; (b) small scale component ${d_{\rm{S}}}$ and low-pass filtered envelope ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$; (c) comparison between large scale component ${d_{\rm{L}}}$ and low-pass filtered envelope ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$(for comparison, adjust the average of ${E_{\rm{L}}}\left( {{d_{\rm{S}}}} \right)$ to the zero-line and magnify the magnitude by a factor of 2).

DownLoad: Full-Size Img PowerPoint

图 8 密度脉动的谱分析($y/\delta $ = 0.1)　(a) 基于傅里叶变换的功率谱密度估计; (b) 基于小波变换的时变谱密度估计

Figure 8. Spectrum analysis of density fluctuation ($y/\delta $ = 0.1): (a) Power spectrum based on Fourier transform; (b) time-varying power spectrum based on wavelet transform.

DownLoad: Full-Size Img PowerPoint

图 9 相近频率的时变谱密度　(a) (60 ± 3) kHz; (b) (113 ± 5) kHz

Figure 9. Time-varying power spectrum of approximate frequency: (a) (60 ± 3) kHz; (b) (113 ± 5) kHz.

DownLoad: Full-Size Img PowerPoint

图 10 不同高度的密度脉动时变谱　(a) $y/\delta $ = 0.4; (b) $y/\delta $ = 0.7; (c) $y/\delta $ = 1.0

Figure 10. Time-varying power spectrum of density fluctuation at different heights: (a) $y/\delta $ = 0.4; (b) $y/\delta $ = 0.7; (c) $y/\delta $ = 1.0.

DownLoad: Full-Size Img PowerPoint

表 1 风洞流场参数

Table 1. Flow conditions

$M{a_\infty }$	${P_0}/{\rm MPa}$	${T_0}/{\rm K}$	${P_\infty }/{\rm Pa}$	${T_\infty }/{\rm K}$	${\rho _\infty }/{\rm kg \cdot {m^{ - 3} }}$	${U_\infty }/{\rm m \cdot {s^{ - 1} }}$	$\mu /{\rm Pa \cdot s}$	${R_e}/{\rm m^{ - 1} }$
3.0	0.1	300	2750	107	0.089	622.5	7.43 × 10^–6	7.49 × 10⁶

DownLoad: CSV

map

[1]	Lee C B, Jiang X Y 2019 Phys. Fluids 31 111301 Google Scholar
[2]	Pan L B, Padoan P, Nordlund A 2018 Astrophys. J. Lett. 866 L17 Google Scholar
[3]	Pan L B, Padoan P, Nordlund A 2019 Astrophys. J. 881 155 Google Scholar
[4]	王正魁, 靳旭红, 朱志斌, 程晓丽 2018 航空学报 39 122244 Google Scholar Wang Z K, Jin X H, Zhu Z B, Cheng X L 2018 Acta Aeronaut. Astronaut. Sin. 39 122244 Google Scholar
[5]	Tian Y F, Jaberi F A, Livescu D 2019 J. Fluid Mech. 880 935 Google Scholar
[6]	Parziale N, Shepherd J, Hornung H 2015 J. Fluid Mech. 781 87 Google Scholar
[7]	He L, Yi S H, Zhao Y X, Tian L F, Chen Z 2011 Chin. Sci. Bull. 56 489 Google Scholar
[8]	何霖, 易仕和, 陆小革 2017 66 024701 Google Scholar He L, Yi S H, Lu X G 2017 Acta Phys. Sin. 66 024701 Google Scholar
[9]	Tian L F, Yi S H, Zhao Y X, He L, Cheng Z Y 2009 Sci. China, Ser. G 52 1357 Google Scholar
[10]	Morkovin M V 1962 Mécanique de la Turbulence 367 380
[11]	Berkooz G, Holmes P, Lumley J L 1993 Annu. Rev. Fluid Mech. 25 539 Google Scholar
[12]	Smith T R, Moehlis J, Holmes P 2005 Nonlinear Dyn. 41 275 Google Scholar
[13]	Schmid P J 2010 J. Fluid Mech. 656 5 Google Scholar
[14]	Schmid P J, Li L, Juniper M P, Pust O 2011 Theor. Comput. Fluid Dyn. 25 249 Google Scholar
[15]	Ruppert-Felsot J, Farge M, Petitjeans P 2009 J. Fluid Mech. 636 427 Google Scholar
[16]	赵玉新, 易仕和, 田立丰, 何霖, 程忠宇 2010 中国科学: 计算科学 53 584 Google Scholar Zhao Y X, Yi S H, Tian L F, He L, Cheng Z Y 2010 Sci. China Ser. E: Technol. Sci. 53 584 Google Scholar
[17]	Rinoshika A, Omori H 2011 Exp. Therm. Fluid Sci. 35 1231 Google Scholar
[18]	Zheng X B, Jiang N 2015 Chin. Phys. B 24 064702 Google Scholar
[19]	Freund A, Ferrante A 2019 J. Fluid Mech. 875 914 Google Scholar
[20]	赵玉新, 易仕和, 何霖, 田立丰 2010 科学通报 55 2004 Google Scholar Zhao Y X, Yi S H, Tian L F, He L, Cheng Z Y 2010 Chin. Sci. Bull. 55 2004 Google Scholar
[21]	Chen Z, Yi S H, He L, Zhu Y Z, Ge Y, Wu Y 2014 J. Visualization 17 345 Google Scholar
[22]	Liu X L, Yi S h, Xu X W, Shi Y, Ouyang T C, Xiong H X 2019 Phys. Fluids 31 074108 Google Scholar
[23]	He L, Yi S H, Zhao Y X, Tian L F, Chen Z 2011 Sci. China, Ser. G 54 1702 Google Scholar
[24]	Taylor G I 1938 Proc. R. Soc. London, Ser. A 164 476 Google Scholar
[25]	Rinoshika A, Zhou Y 2005 J. Fluid Mech. 524 229 Google Scholar
[26]	Van Doorne C, Westerweel J 2007 Exp. Fluids 42 259 Google Scholar
[27]	Ganapathisubramani B, Lakshminarasimhan K, Clemens N T 2007 Exp. Fluids 42 923 Google Scholar
[28]	Vétel J, Garon A, Pelletier D 2010 Exp. Fluids 48 441 Google Scholar
[29]	曹晖, 赖明, 白绍良 2004 工程力学 21 109 Google Scholar Cao H, Lai M, Bai S L 2004 Eng. Mech. 21 109 Google Scholar
[30]	Spanos P D, Failla G 2004 J. Eng. Mech. 130 952 Google Scholar
[31]	Mouri H, Kubotani H, Fujitani T, Niino H, Takaoka M 1999 J. Fluid Mech. 389 229 Google Scholar
[32]	Mallat S G 1989 IEEE Trans. Pattern Anal. Mach. Intell. 11 674 Google Scholar
[33]	Rinoshika A, Watanabe S 2010 Exp. Therm. Fluid Sci. 34 1389 Google Scholar
[34]	Hutchins N, Marusic I 2007 Philos. Trans. R. Soc. London, Ser. A 365 647 Google Scholar
[35]	Mathis R, Hutchins N, Marusic I 2009 J. Fluid Mech. 628 311 Google Scholar
[36]	Mathis R, Monty J P, Hutchins N, Marusic I 2009 Phys. Fluids 21 111703 Google Scholar
[37]	He G S, Pan C, Feng L H, Gao Q, Wang J J 2016 J. Fluid Mech. 792 274 Google Scholar
[38]	He G S, Wang J J, Rinoshika A 2019 Phys. Rev. E 99 053105 Google Scholar
[39]	Gurley K, Kareem A 1999 Eng. Struct. 21 149 Google Scholar
[40]	白泉, 边晶梅, 康玉梅 2018 小波理论在工程结构振动分析中的应用 (北京: 清华大学出版社) 第32−49页 Bai Q, Bian J M, Kang Y M 2018 Application of Wavelet Theory in Vibration Analysis of Engineering structures (Beijing: Tsinghua Univesity Press) pp32−49 (in Chinese)
[41]	何霖 2011 博士学位论文 (长沙: 国防科学技术大学) He L 2011 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[42]	Eswaran V, Pope S 1988 Phys. Fluids 31 506 Google Scholar
[43]	Antonia R A, Mi J 1993 J. Fluid Mech. 250 531 Google Scholar

[1]	Luo Shi-Chao, Wu Li-Yin, Chang Yu. Mechanism analysis of magnetohydrodynamic control in hypersonic turbulent flow. Acta Physica Sinica, 2022, 71(21): 214702. doi: 10.7498/aps.71.20220941
[2]	Liu Xin-Yu, Yang Su-Hui, Liao Ying-Qi, Lin Xue-Tong. Laser underwater ranging based on wavelet transform. Acta Physica Sinica, 2021, 70(18): 184205. doi: 10.7498/aps.70.20210569
[3]	Tang Bing-Liang, Guo Shan-Guang, Song Guo-Zheng, Luo Yan-Hao. Experimental study on supersonic plate boundary layer transition under pulsed arc plasma excitation control. Acta Physica Sinica, 2020, 69(15): 155201. doi: 10.7498/aps.69.20200216
[4]	Xu Hao, Wang Cong, Lu Hong-Zhi, Huang Wen-Hu. Experimental study on submerged supersonic gaseous jet induced tail cavity. Acta Physica Sinica, 2018, 67(1): 014703. doi: 10.7498/aps.67.20171617
[5]	He Lin, Yi Shi-He, Lu Xiao-Ge. Experimental study on the density characteristics of a supersonic turbulent boundary layer. Acta Physica Sinica, 2017, 66(2): 024701. doi: 10.7498/aps.66.024701
[6]	Zhu Yang-Zhu, Yi Shi-He, Kong Xiao-Ping, He Lin. Fine structures and characteristics on supersonic flow over backward facing step with tangential injection. Acta Physica Sinica, 2015, 64(6): 064701. doi: 10.7498/aps.64.064701
[7]	Gang Dun-Dian, Yi Shi-He, Zhao Yun-Fei. Experimental and numerical studies of supersonic flow over circular protuberances on a flat plate. Acta Physica Sinica, 2015, 64(5): 054705. doi: 10.7498/aps.64.054705
[8]	Zhu Yang-Zhu, Yi Shi-He, Kong Xiao-Ping, Quan Peng-Cheng, Chen Zhi, Tian Li-Feng. Fine structures and the unsteadiness characteristics of supersonic flow over backward facing step via NPLS. Acta Physica Sinica, 2014, 63(13): 134701. doi: 10.7498/aps.63.134701
[9]	Zhu Yang-Zhu, Yi Shi-He, Chen Zhi, Ge Yong, Wang Xiao-Hu, Fu Jia. Experimental investigation on aero-optical aberration of the supersonic flow passing through an optical dome with gas injection. Acta Physica Sinica, 2013, 62(8): 084219. doi: 10.7498/aps.62.084219
[10]	Yu Hai-Jun, Du Jian-Ming, Zhang Xiu-Lan. Wavelet transform of coherent state. Acta Physica Sinica, 2012, 61(16): 164205. doi: 10.7498/aps.61.164205
[11]	Gan Tian, Feng Shao-Tong, Nie Shou-Ping, Zhu Zhu-Qing. Image fusion algorithm based on block-DCT in wavelet domain. Acta Physica Sinica, 2011, 60(11): 114205. doi: 10.7498/aps.60.114205
[12]	Fu Mao-Jing, Zhuang Jian-Jun, Hou Feng-Zhen, Ning Xin-Bao, Zhan Qing-Bo, Shao Yi. Extracting human gait series based on the wavelet transform. Acta Physica Sinica, 2010, 59(6): 4343-4350. doi: 10.7498/aps.59.4343
[13]	Zhao Wen-Shan, He Yi-Gang. An improved method for implementation of wavelet transform utilizing switched-current filters. Acta Physica Sinica, 2009, 58(2): 843-851. doi: 10.7498/aps.58.843
[14]	Deng Yu-Qiang, Cao Shi-Ying, Yu Jing, Xu Tao, Wang Qing-Yue, Zhang Zhi-Gang. Carrier-envelope phase extraction with wavelet-transform technique of amplified ultrashort optical pulses. Acta Physica Sinica, 2008, 57(11): 7017-7021. doi: 10.7498/aps.57.7017
[15]	Hu Qin-Chun, He Yi-Gang, Guo Di-Xin, Li Hong-Min. Analog implementation of wavelet transform based on switched-current filter circuits. Acta Physica Sinica, 2006, 55(2): 641-647. doi: 10.7498/aps.55.641
[16]	Deng Yu-Qiang, Xing Qi-Rong, Lang Li-Ying, Chai Lu, Wang Qing-Yue, Zhang Zhi-Gang. Wavelet-transform in terahertz time-domain spectroscopy. Acta Physica Sinica, 2005, 54(11): 5224-5227. doi: 10.7498/aps.54.5224
[17]	Deng Yu-Qiang, Zhang Zhi-Gang, Chai Lu, Wang Qing-Yue. Effects of noise on spectral phase reconstruction with wavelet analysis. Acta Physica Sinica, 2005, 54(9): 4176-4181. doi: 10.7498/aps.54.4176
[18]	You Rong-Yi, Chen Zhong, Xu Shen-Chu, Wu Bo-Xi. Study on phase-space reconstruction of chaotic signal based on wavelet transform. Acta Physica Sinica, 2004, 53(9): 2882-2888. doi: 10.7498/aps.53.2882
[19]	Lian Qi-Xiang, Guo Hui. The sweep down flow and “contra-hairpin vortex” in a turbulent boundary layer. Acta Physica Sinica, 2004, 53(7): 2226-2232. doi: 10.7498/aps.53.2226
[20]	Gong An-Long, Li Rui-Qu, Li Cun-Bao. . Acta Physica Sinica, 2002, 51(5): 1068-1074. doi: 10.7498/aps.51.1068

Catalog

Vol. 69, Issue 21 - 2020-11-05

Metrics

Abstract views: 7002
PDF Downloads: 104
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板