-
This paper proposes an underwater ranging method based on wavelet transform. First, according to the band-pass filtering characteristics of the wavelet transform, the time-domain signal is decomposed in the frequency domain. The wavelet basis functions with high similarity are established. These wavelet basis functions contain complete frequency domain information of time-domain signals. This method can improve the ability to decompose frequency domain of time-domain signals and extract the information about the effective frequency domain. Then, using the multiple frequency domain decomposition approximations, the effective frequency domain information contained in the time domain signal is completely extracted. The time-frequency signal of wavelet time-frequency fusion ranging takes the energy consistency of the time-frequency domain signal as the link and uses the binary spline interpolation structure to realize the time-frequency combination of the signal. In this method, the time-domain signal is first decomposed and filtered by wavelet time-domain to obtain more complete time-domain effective information. But at this time, the time-domain signal is the superimposed form of frequency-domain information, so the energy domain information contained in the time-frequency signal is decomposed into the wavelet frequency domain through the binary spline interpolation, and the energy expression form of the time-frequency signal can be obtained. The target is locked by finding the position of the maximum value of energy corresponding to the time-frequency domain of the signal to achieve the purpose of precise ranging. By performing the wavelet multi-layer time-domain decomposition filtering first, the frequency domain decomposition range can be effectively reduced, thereby avoiding data redundancy and reducing the ability to realize the effective frequency domain resolution. By using this method we successively carry out continuous light underwater ranging experiments with different attenuation length water bodies and different modulation frequencies, and analyze the influence of this method on continuous light underwater detection. Experiments verify that this ranging method successfully achieves the accurate measurement of targets within 8 attenuation lengths within an output power of 2.3 W, and its ranging accuracy is less than 1 cm; the use of wavelet time-frequency fusion ranging can pass the frequency domain energy decomposition capability enhancement, to a certain extent, compensates for the measurement error caused by the significant attenuation of the effective signal. Therefore, the ranging method can be applied to signals with complex frequency domain information or including a bandwidth. [1] Alen N, Pellen F, Brun G L 2017 Appl. Opt. 56 736
Google Scholar
[2] 宋红, 张云菲, 吴超鹏, 等 2019 红外与激光工程 48 4
Google Scholar
Song H, Zhang Y F, Wu C P, et al. 2019 Infrared Laser Eng. 48 4
Google Scholar
[3] 胡波, 张云菲, 吴超鹏, 杨永, 陈宗恒, 宋宏, 陶军 2019 红外与激光工程 48 10
Google Scholar
Hu B, Zhang Y F, Wu C P, Yang Y, Chen Z H, Song H, Tao J 2019 Infrared Laser Eng. 48 10
Google Scholar
[4] Abshire J B, Sun X L, Riris H, et al. 2003 23rd International Geoscience and Remote Sensing Symposium (IGARSS 2003) Toulouse, France, July 21−25, 2003 p1534
[5] McLennan D 2010 Proc. SPIE 7826 782610
[6] 彭志兴, 周保琢, 陈华, 张志, 谭平 2018 激光应用技术 48 7
Google Scholar
Peng A, Zhi X, Zhou B Z, Chen H, Zhang Z, Tan P 2018 Laser Application Technology 48 7
Google Scholar
[7] 丁燕 2007 博士学位论文 (上海: 同济大学)
Ding Y 2007 Ph. D. Dissertation (Shanghai: Tongji University) (in Chinese)
[8] 李兵 2013 硕士学位论文 (西安: 中国科学院西安光学精密机械研究所)
Li B 2013 M. S. Thesis (Xi’an: Xi’an Institute of Optics and Fine Mechanics of CAS) (in Chinese)
[9] Kabashnikov V, Kuntsevich B 2017 Appl. Opt. 56 8378
Google Scholar
[10] Matwyschuk A 2014 Appl. Opt. 53 44
Google Scholar
[11] Matwyschuk A 2017 Appl. Opt. 56 7766
Google Scholar
[12] Matwyschuk A 2020 Appl. Opt. 59 7670
Google Scholar
[13] Ma M T, Kanda M, Crawford M L 1985 Proc. IEEE 73 388
Google Scholar
[14] Baumann E, Deschenes J D, Giorgetta F R, Swann W C, Coddington L, Newbury N R 2014 Opt. Lett. 39 4776
Google Scholar
[15] Yu Y, Liu B, Chen Z 2018 Appl. Opt. 57 7733
Google Scholar
[16] 隋修宝, 陈钱, 顾国华, 徐彤 2011 红外与激光工程 40 1928
Google Scholar
Sui X B, Chen Q, Gu G H, Xu T 2011 Infrared Laser Eng. 40 1928
Google Scholar
[17] 钟琳 2020 应用激光 40 129
Google Scholar
Zhong L 2020 Applied Laser 40 129
Google Scholar
[18] 路明, 孔德浩, 苏益德 2018 激光与红外 48 1223
Google Scholar
Lu M, Kong D H, Su Y D 2018 Laser & Infrared 48 1223
Google Scholar
[19] 彭冲 2016 博士学位论文 (长沙: 湖南师范大学)
Peng C 2016 Ph. D. Dissertation (Changsha: Hunan Normal University) (in Chinese)
[20] 朱金龙 2017 博士学位论文 (天津: 河北工业大学)
Zhu J L 2017 Ph. D. Dissertation (Tianjin: Hebei University of Technology) (in Chinese)
[21] 吴军, 桑明煌, 周行, 王贤平, 徐猛 2016 光子学报 45 31
Google Scholar
Wu J, Sang M H, Zhou X, Wang X P, Xu M 2016 Acta Photon. Sin. 45 31
Google Scholar
-
图 1 激光水下探测光学系统
Figure 1. Laser underwater detection optical system.
图 2 基于小波变换的时频分析方法对水下目标的探测过程
Figure 2. Detection process of underwater targets based on wavelet transform time-frequency analysis method.
图 3 回波信号与参考信号波形及相应运算结果 (a) 频率-相位差波形图; (b) 图(a)的傅里叶逆运算结果; (c), (d) 基准位置和1 m目标位置的时频能量极值的时域表示
Figure 3. Echo signal and reference signal waveforms and corresponding calculation results: (a) Frequency vs. phase difference waveform diagram; (b) the Fourier inverse calculation result of panel (a); (c) and (d) time-frequency energy extreme value positions of the reference position and 1 m position of the target in the time-domain.
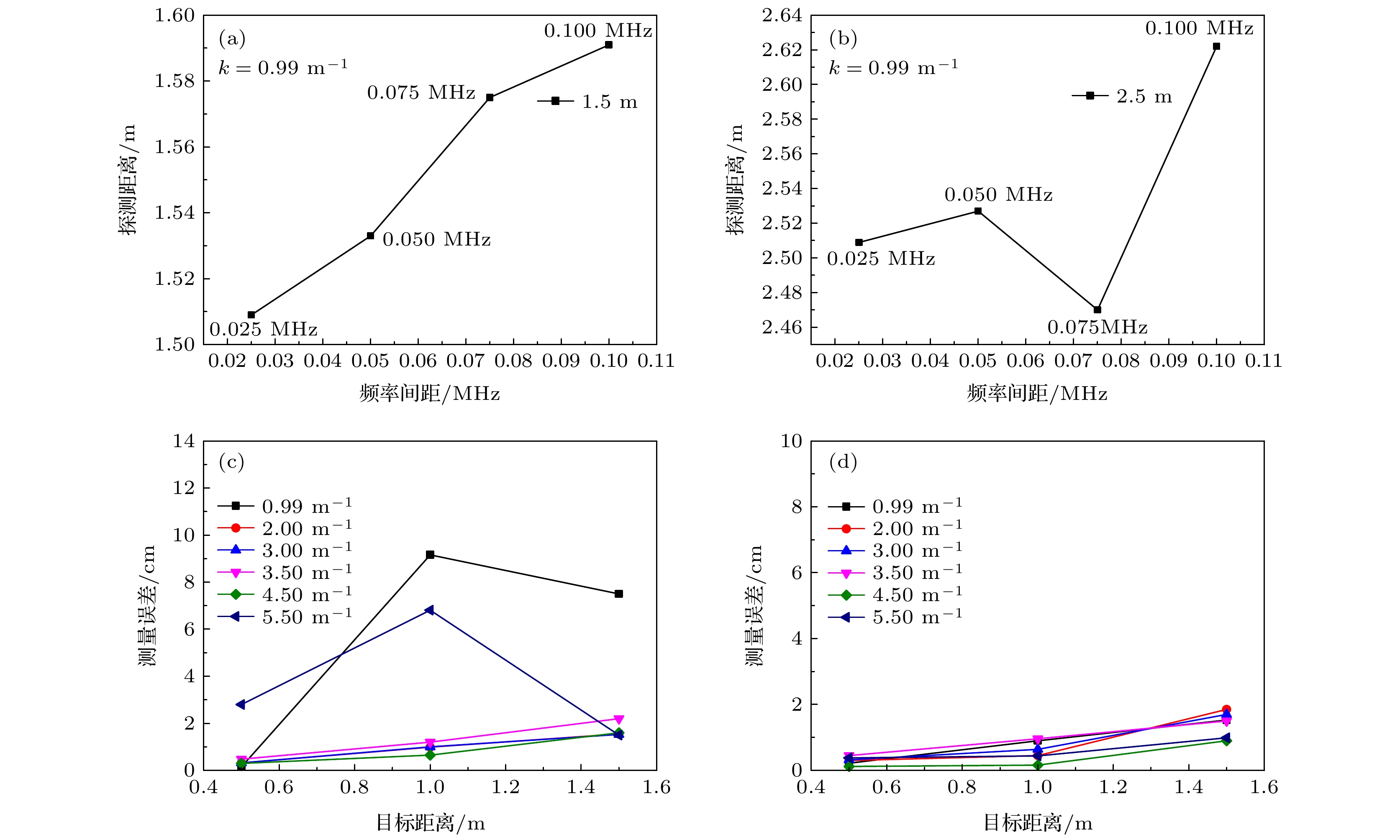
图 4 不同频率分解间隔对探测目标的影响 (a), (b) 同一水体条件下, 不同频率分解间隔时1.5和2.5 m目标的测量误差; (c), (d) 不同衰减系数的水体条件下, 频域分解间隔为0.1和0.025 MHz时不同目标距离的测量误差
Figure 4. Influences of different frequency decomposition intervals on detection targets: (a), (b) Measurement error at differently frequency decomposition intervals for 1.5 and 2.5 m under the same water body condition; (c), (d) under the water bodies with different attenuation coefficient conditions, the measurement error different distance targets at frequency domain decomposition interval of 0.1 and 0.025 MHz, .
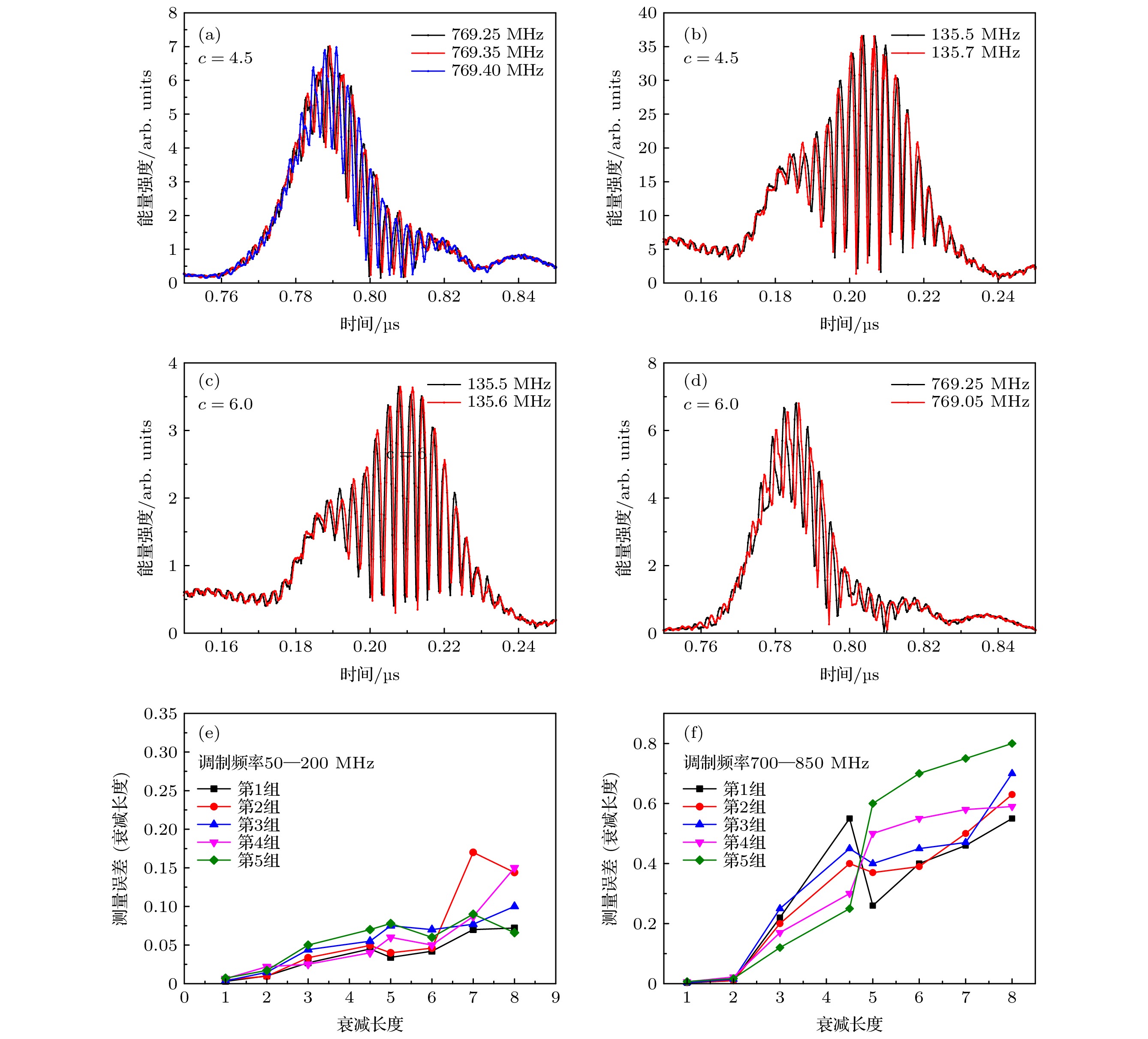
图 5 调制频率(50—200 MHz和700—850 MHz)对小波时频融合测距方法的影响 (a)—(d)在4.5和6个衰减长度下, 探测目标在极值频率位置的时域能量表示; (e), (f) 两频率范围下不同衰减长度对应的测量误差
Figure 5. Influences of modulation frequency on wavelet time-frequency fusion ranging method, where the modulation frequency is a range of 50 to 200 MHz and 700 to 850 MHz: (a)–(d) Time-frequency domain energy extreme frequency position of measurement target under the two attenuation lengths of 4.5 and 6; (e), (f) measurement errors for different attenuation length at the two frequency ranges.
图 6 基于小波变换的时频融合测距结果 (a)—(f)对于衰减长度为1—8.2的水体, 该测距方法测量的测量误差以及均方根
Figure 6. Time-frequency fusion ranging results based on wavelet transform: (a)–(f) Ranging error and root mean square detected by this ranging method for water bodies with attenuation lengths of 1 to 8.2.
表 1 不同衰减系数与距离功率的关系
Table 1. Relationship between different attenuation coefficients and distance power.
样本 目标距离/m 回波信号
强度/mW衰减
系数/m–1平均衰减
系数/m–11 0 26.5 — 0.99 0.25 18.5 0.99 0.5 9.8 0.99 1 3.6 0.99 2 0 50 — 2.00 0.25 18.4 1.99 0.5 6.5 1.99 0.6 4.5 2.01 3 0 150 — 3.00 0.2 45 3.00 0.4 13.5 3.01 0.6 4.1 2.99 4 0 150 — 3.50 0.3 18.4 3.50 0.5 4.5 3.51 0.6 2.2 3.49 5 0 200 — 4.50 0.1 81.5 4.50 0.2 33 4.51 0.3 13.5 4.49 6 0 200 — 5.50 0.1 66 5.54 0.15 39 5.45 0.25 12.7 5.51 
DownLoad: CSV
-
[1] Alen N, Pellen F, Brun G L 2017 Appl. Opt. 56 736
Google Scholar
[2] 宋红, 张云菲, 吴超鹏, 等 2019 红外与激光工程 48 4
Google Scholar
Song H, Zhang Y F, Wu C P, et al. 2019 Infrared Laser Eng. 48 4
Google Scholar
[3] 胡波, 张云菲, 吴超鹏, 杨永, 陈宗恒, 宋宏, 陶军 2019 红外与激光工程 48 10
Google Scholar
Hu B, Zhang Y F, Wu C P, Yang Y, Chen Z H, Song H, Tao J 2019 Infrared Laser Eng. 48 10
Google Scholar
[4] Abshire J B, Sun X L, Riris H, et al. 2003 23rd International Geoscience and Remote Sensing Symposium (IGARSS 2003) Toulouse, France, July 21−25, 2003 p1534
[5] McLennan D 2010 Proc. SPIE 7826 782610
[6] 彭志兴, 周保琢, 陈华, 张志, 谭平 2018 激光应用技术 48 7
Google Scholar
Peng A, Zhi X, Zhou B Z, Chen H, Zhang Z, Tan P 2018 Laser Application Technology 48 7
Google Scholar
[7] 丁燕 2007 博士学位论文 (上海: 同济大学)
Ding Y 2007 Ph. D. Dissertation (Shanghai: Tongji University) (in Chinese)
[8] 李兵 2013 硕士学位论文 (西安: 中国科学院西安光学精密机械研究所)
Li B 2013 M. S. Thesis (Xi’an: Xi’an Institute of Optics and Fine Mechanics of CAS) (in Chinese)
[9] Kabashnikov V, Kuntsevich B 2017 Appl. Opt. 56 8378
Google Scholar
[10] Matwyschuk A 2014 Appl. Opt. 53 44
Google Scholar
[11] Matwyschuk A 2017 Appl. Opt. 56 7766
Google Scholar
[12] Matwyschuk A 2020 Appl. Opt. 59 7670
Google Scholar
[13] Ma M T, Kanda M, Crawford M L 1985 Proc. IEEE 73 388
Google Scholar
[14] Baumann E, Deschenes J D, Giorgetta F R, Swann W C, Coddington L, Newbury N R 2014 Opt. Lett. 39 4776
Google Scholar
[15] Yu Y, Liu B, Chen Z 2018 Appl. Opt. 57 7733
Google Scholar
[16] 隋修宝, 陈钱, 顾国华, 徐彤 2011 红外与激光工程 40 1928
Google Scholar
Sui X B, Chen Q, Gu G H, Xu T 2011 Infrared Laser Eng. 40 1928
Google Scholar
[17] 钟琳 2020 应用激光 40 129
Google Scholar
Zhong L 2020 Applied Laser 40 129
Google Scholar
[18] 路明, 孔德浩, 苏益德 2018 激光与红外 48 1223
Google Scholar
Lu M, Kong D H, Su Y D 2018 Laser & Infrared 48 1223
Google Scholar
[19] 彭冲 2016 博士学位论文 (长沙: 湖南师范大学)
Peng C 2016 Ph. D. Dissertation (Changsha: Hunan Normal University) (in Chinese)
[20] 朱金龙 2017 博士学位论文 (天津: 河北工业大学)
Zhu J L 2017 Ph. D. Dissertation (Tianjin: Hebei University of Technology) (in Chinese)
[21] 吴军, 桑明煌, 周行, 王贤平, 徐猛 2016 光子学报 45 31
Google Scholar
Wu J, Sang M H, Zhou X, Wang X P, Xu M 2016 Acta Photon. Sin. 45 31
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4473
- PDF Downloads: 96
- Cited By: 0
