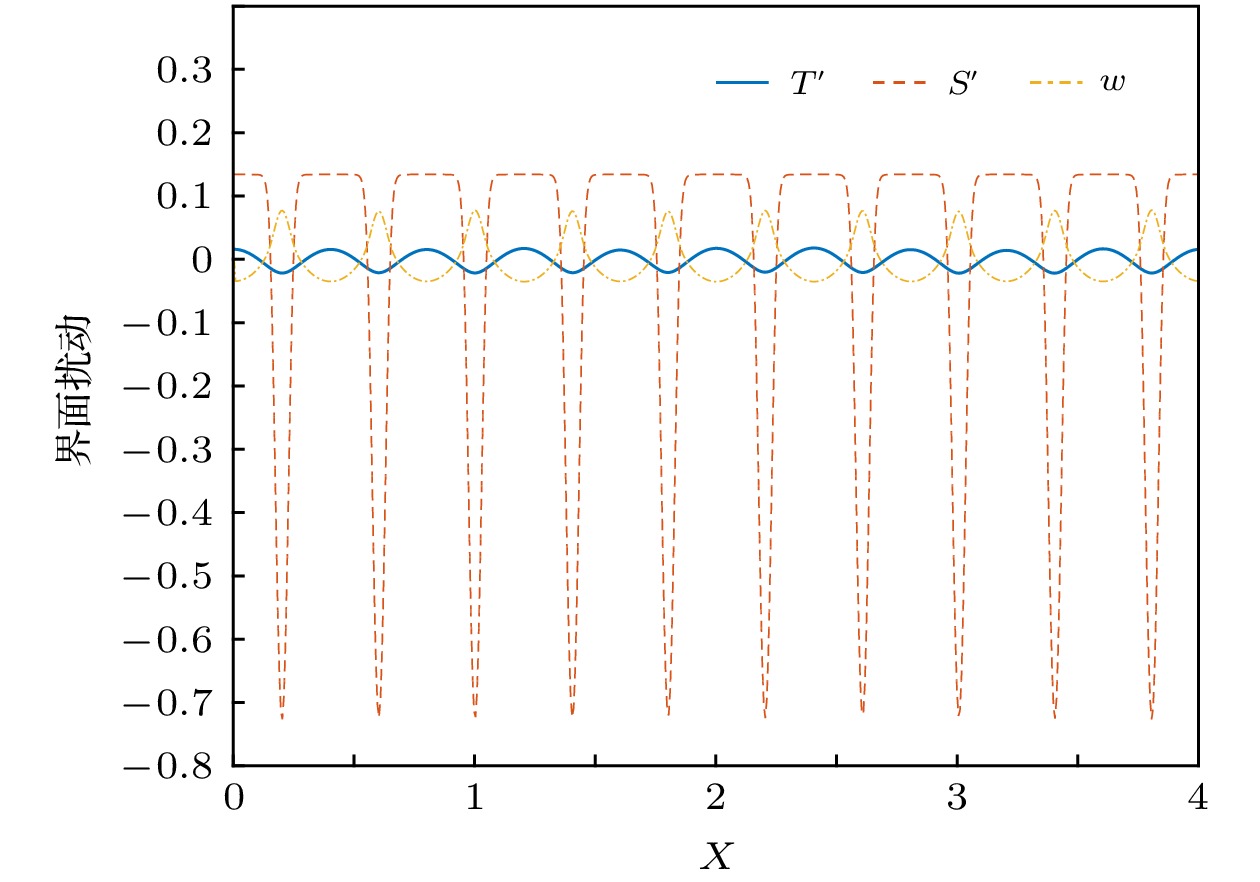
-
Simultaneous occurrence of temperature gradient and solute gradient at the fluid-sediment interface is conducive to the onset of salt-finger convection, which may in turn cause adverse effects on fluid mechanism. Ignoring the existence of salt finger would lead to numerical errors or sometimes even qualitative error in calculation of vertical mass fluxes. In this paper, a single-domain approach is adopted for the two-dimensional numerical model of flow coupled temperature and solute in a composite region made up of an upper fluid layer and an underlying saturated porous layer to investigate the evolution of the double diffusion convection of salt-finger form at the fluid-saturated porous interface. Darcian model describing the porous medium and incompressible Navier-Stokes equations in the fluid layer are solved at the same time, where different heat capacities, thermal conductivities and solute diffusion coefficients are considered. Three cases for
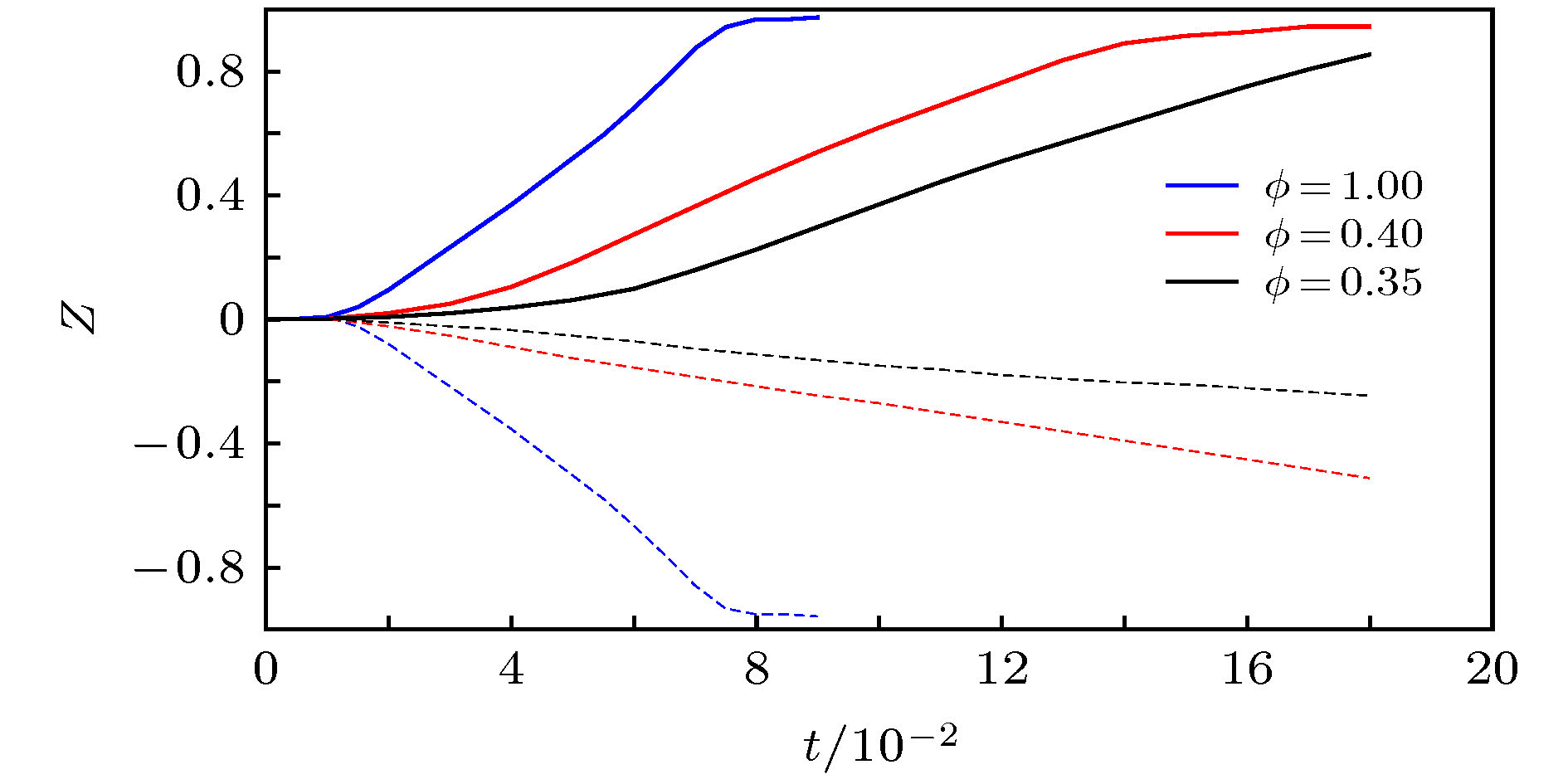
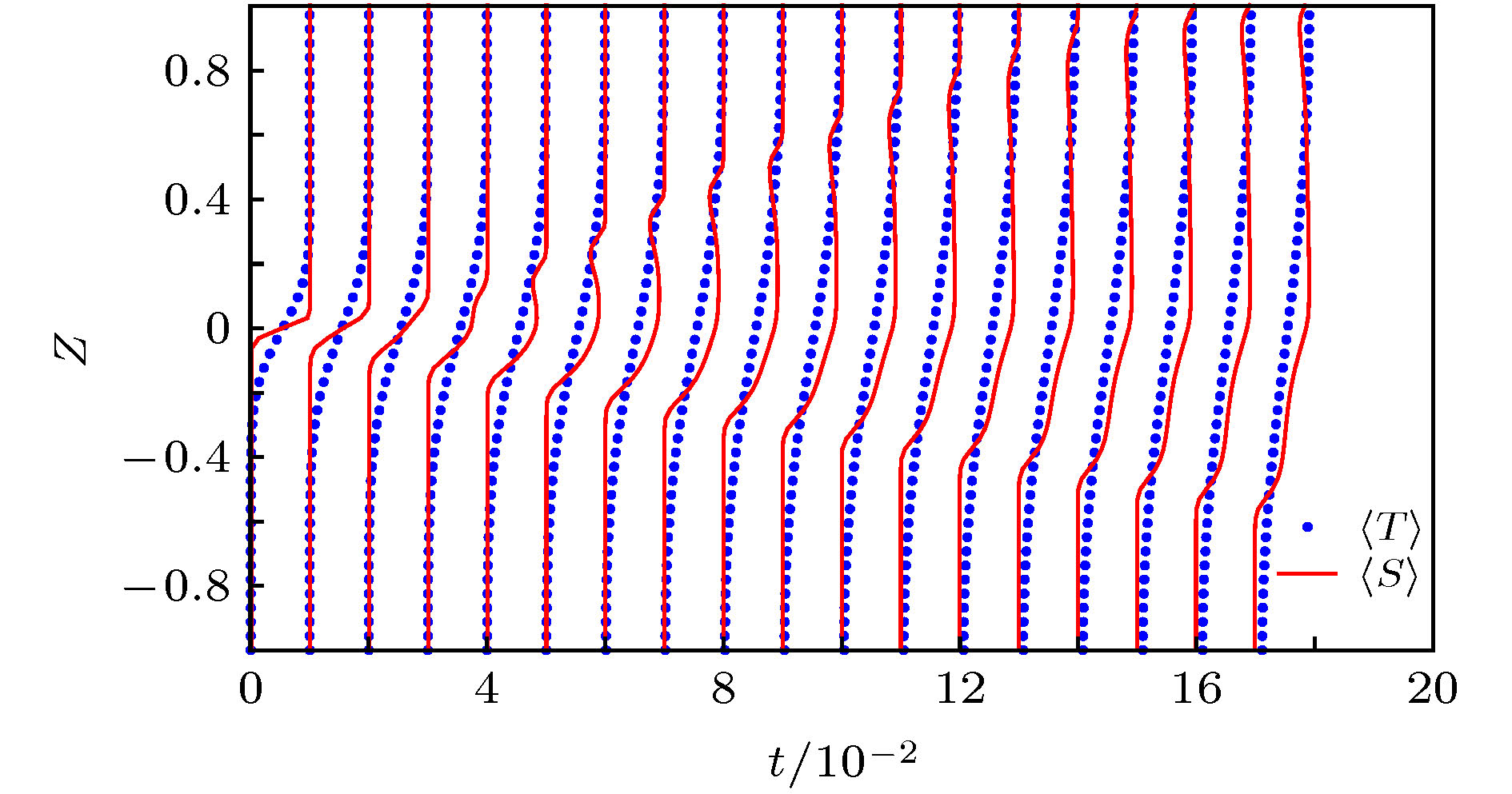
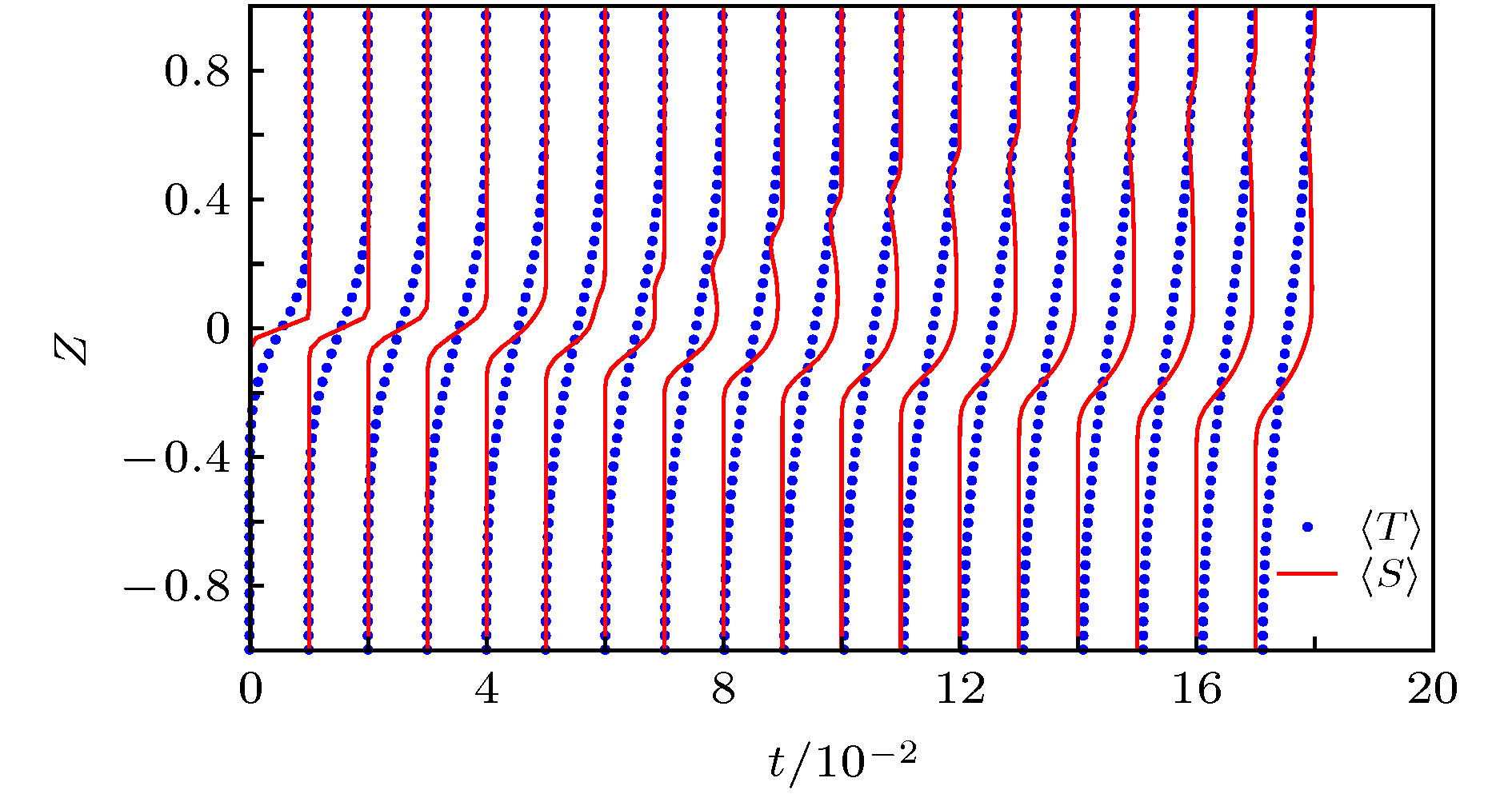
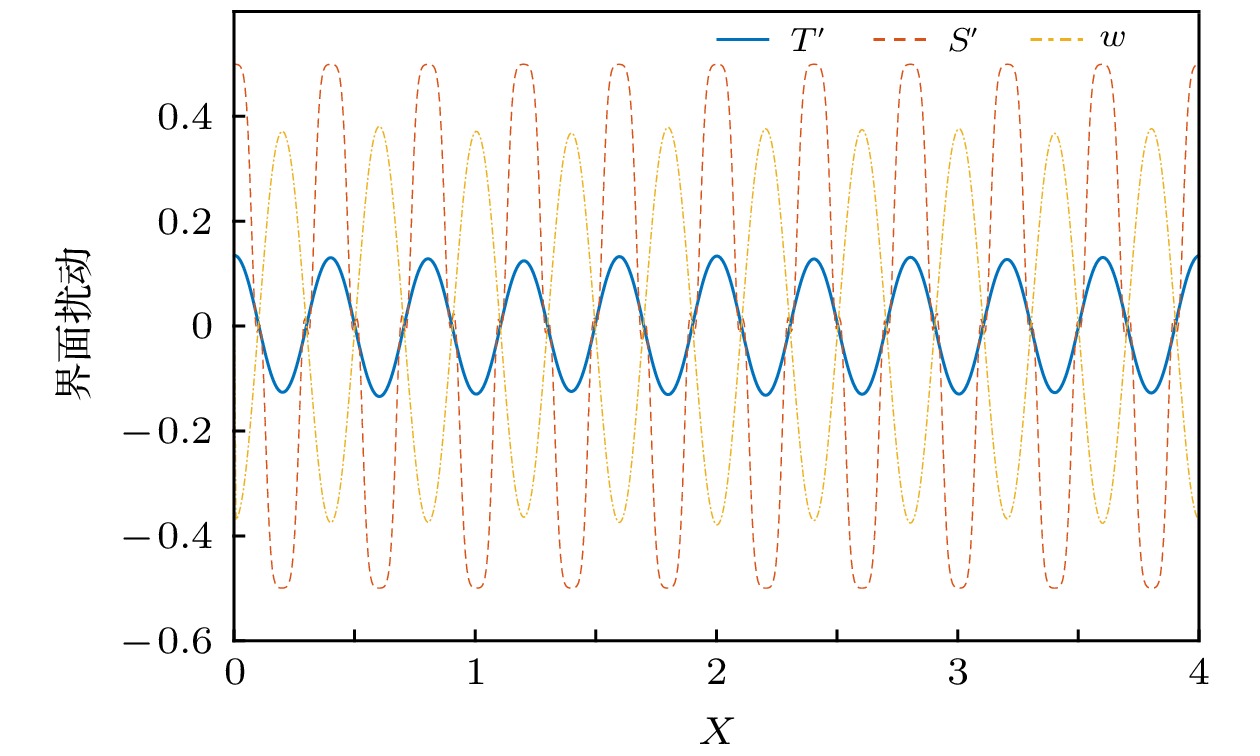
$ \phi = 0.3{{5}},\;0.4{{0}},\;1 $ are considerded to study the evolution process and structure of salt fingers. The evolution process of salt finger is divided into three stages: diffusion stage, linear growth stage and slow growth stage. For all cases, the kinetic energy is transformed rapidly at linear growth stage, which promotes the mixture of momentum, temperature and salinity at the interface. Then at the slow growth stage, the kinetic energy conversion rate becomes slower before finally the kinetic energy is dissipated by the viscosity and friction. The results show that unlike the salt finger structure in stratified fluid, an asymmetric structure of salt finger is discovered where finger in the porous medium is shorter and wider. The existence of solid skeleton in porous medium hinders the growth of salt finger and reduces the vertical mass flux. Compared with the temperature, the salinity fluctuates more greatly at the interface, which also means that the effect of salt finger on salinity is greater than that of temperature. It is found that the higher the porosity, the faster the growth of thickness of salt finger interface is. Under the condition of high porosity, the potential energy stored by the unstable stratification of salinity is converted much more into kinetic energy, which increases the transport of heat and mass in the vertical direction and thus enhances the mixture capability of salt finger in the vertical direction.-
Keywords:
- porous layer /
- interface /
- salt finger /
- laminar flow
[1] Schmitt R W 1983 Phys. Fluids 26 2373
Google Scholar
[2] Slim A C, Bandi M M, Miller J C, Mahadevan L 2013 Phys. Fluids 25 024101
Google Scholar
[3] Hage E, Tilgner A 2010 Phys. Fluids 22 11
Google Scholar
[4] Rehman F, Singh O P 2017 Geophys. Astrophys. Fluid Dyn. 111 1
Google Scholar
[5] Chen F, Chen C F 1993 Int. J. Heat Mass Transfer 36 793
Google Scholar
[6] Piacsek S A, Toomre J 1980 Elsevier Oceanogr. Ser. 28 193
Google Scholar
[7] Özgökmen T M, Esenkov O E, Olson D B 1998 J. Mar. Res. 56 463
Google Scholar
[8] Kluikov Y Y, Karlin L N 1995 GMS 94 287
Google Scholar
[9] Schmitt R W, Ledwell J R, Montgomery E T, Polzin K, Toole J 2005 Science 308 685
Google Scholar
[10] 罗莹莹, 詹杰民, 李毓湘 2008 57 2306
Google Scholar
Luo Y, Zhan J, Li S 2008 Acta Phys. Sin. 57 2306
Google Scholar
[11] 郑来运, 赵秉新, 杨建青 2020 69 074701
Google Scholar
Zheng L Y, Zhao B X, Yang J Q 2020 Acta Phys. Sin. 69 074701
Google Scholar
[12] Chen F, Chen C F 1988 J. Heat Transfer 110 403
Google Scholar
[13] Cooper C A, Glass R J, Tyler S W 2001 Water Resour. Res. 37 2323
Google Scholar
[14] Werner C L 2007 Ph. D. Dissertation (Tallahassee: Florida State University)
[15] Singh O P, Srinivasan J 2014 Phys. Fluids 26 2373
Google Scholar
[16] Shen C Y 1993 Phys. Fluids 5 2633
Google Scholar
[17] Fernandes A M, Krishnamurti R 2010 J. Fluid Mech. 658 148
Google Scholar
[18] Copley S M, Giamei A F, Johnson S M, Hornbecker M F 1970 Metall. Trans. 1 2193
Google Scholar
[19] Basu A J, Khalili A 1999 Phys. Fluids 11 1395
Google Scholar
[20] Shen C J, Jin G Q, Xin P, Kong J, Li L 2015 Water Resour. Res. 51 4301
Google Scholar
[21] Beavers G S, Joseph D D 1967 J. Fluid Mech. 30 11
Google Scholar
[22] Kuznetsov A V 1997 Int. Commun. Heat Mass Transfer 24 401
Google Scholar
[23] 娄钦, 黄一帆, 李凌 2019 68 214702
Google Scholar
Lou Q, Huang Y, Li L 2019 Acta Phys. Sin. 68 214702
Google Scholar
[24] Caltagirone J P 1975 J. Fluid Mech. 72 269
Google Scholar
[25] Zhan J M, Luo Y Y, Li Y S 2008 Appl. Math. Modell. 32 873
Google Scholar
[26] Zhang X F, Wang L L, Lin C, Zhu H, Zeng C 2018 Phys. Fluids 30 022110
Google Scholar
[27] Garaud P 2018 Annu. Rev. Fluid Mech. 50 275
Google Scholar
[28] Kunze E 1987 J. Mar. Res. 45 533
Google Scholar
-
图 1 水沙交界面盐指计算模型及初始条件
Figure 1. Computational model and initial condition of salt finger at fluid-sediment interface.
图 2 盐度场的三个演变过程 (a) 扩散阶段; (b) 线性增长期; (c) 缓慢增长期
Figure 2. Three evolution phases of the salinity field: (a) Early formation; (b) linear growth of fingers; (c) the slow growth period.
图 3 上下层界面位置随时间变化, 其中实线和虚线分别表示上层和下层
Figure 3. Positions of the upper and lower mixed-finger interface versus time for all experiments. The solid line and dashed line represent the upper and lower layers, respectively.
图 4 温度与盐度的分布图 (a)
$\phi = 0.40$ 工况,$t = 0.15$ 时$\left\langle T \right\rangle $ ,$\left\langle S \right\rangle $ 剖面; (b) S云图; (c) T云图Figure 4. Horizontally averaged T and S profiles (a) for
$\phi = 0.40$ at$t = 0.15$ with salinity field in (b) and temperature field in (c).
图 5
$\phi = 0.40$ 工况界面盐指的传热传质效应Figure 5. Heat and salinity transfer at the interface for
$\phi = 0.40$ .
图 6
$\phi = 0.35$ 工况界面盐指的传热传质效应Figure 6. Heat and salinity transfer at the interface for
$\phi = 0.35$ .
图 7 瞬时速度场分布图 (a)
$\phi = {1}$ 工况,$t = 0.075$ 时; (b)$\phi = 0.40$ 工况,$t = 0.18$ 时Figure 7. Velocity field for (a)
$\phi = {1}$ at$t = 0.075$ and (b)$\phi = 0.40$ at$t = 0.18$ .
图 8 全域总动能演变
Figure 8. Evolution of basin-integrated kinetic energy.
图 9
$\phi = {1}$ 工况,$t = 0.05$ 时界面$z = 0$ 处温度、盐度和垂向速度(缩小100倍)分布图Figure 9.
$T',\; S'$ and w along$z = 0$ for$\phi = 0.35$ at$t = 0.10$ (w is scaled by 100).
图 10
$\phi = 0.40$ 工况,$t = 0.10$ 时界面$z = 0$ 处温度、盐度和垂向速度(缩小100倍)分布图Figure 10.
$T',\; S'$ and w along$z = 0$ for$\phi = 0.35$ at$t = 0.10$ (w is scaled by 100).
图 11 三个工况界面处
$z = 0$ 通量比${R_{\rm{f}}}$ 随时间变化Figure 11. Flux ratio
${R_{\rm{f}}}$ along$z = 0$ versus time for all cases表 1 无量纲参数取值
Table 1. Values of dimensionless parameters.
无量纲参数 Pr Le Ra N Φ 取值 7 100 50000 2 0.35, 0.4, 1 
DownLoad: CSV
-
[1] Schmitt R W 1983 Phys. Fluids 26 2373
Google Scholar
[2] Slim A C, Bandi M M, Miller J C, Mahadevan L 2013 Phys. Fluids 25 024101
Google Scholar
[3] Hage E, Tilgner A 2010 Phys. Fluids 22 11
Google Scholar
[4] Rehman F, Singh O P 2017 Geophys. Astrophys. Fluid Dyn. 111 1
Google Scholar
[5] Chen F, Chen C F 1993 Int. J. Heat Mass Transfer 36 793
Google Scholar
[6] Piacsek S A, Toomre J 1980 Elsevier Oceanogr. Ser. 28 193
Google Scholar
[7] Özgökmen T M, Esenkov O E, Olson D B 1998 J. Mar. Res. 56 463
Google Scholar
[8] Kluikov Y Y, Karlin L N 1995 GMS 94 287
Google Scholar
[9] Schmitt R W, Ledwell J R, Montgomery E T, Polzin K, Toole J 2005 Science 308 685
Google Scholar
[10] 罗莹莹, 詹杰民, 李毓湘 2008 57 2306
Google Scholar
Luo Y, Zhan J, Li S 2008 Acta Phys. Sin. 57 2306
Google Scholar
[11] 郑来运, 赵秉新, 杨建青 2020 69 074701
Google Scholar
Zheng L Y, Zhao B X, Yang J Q 2020 Acta Phys. Sin. 69 074701
Google Scholar
[12] Chen F, Chen C F 1988 J. Heat Transfer 110 403
Google Scholar
[13] Cooper C A, Glass R J, Tyler S W 2001 Water Resour. Res. 37 2323
Google Scholar
[14] Werner C L 2007 Ph. D. Dissertation (Tallahassee: Florida State University)
[15] Singh O P, Srinivasan J 2014 Phys. Fluids 26 2373
Google Scholar
[16] Shen C Y 1993 Phys. Fluids 5 2633
Google Scholar
[17] Fernandes A M, Krishnamurti R 2010 J. Fluid Mech. 658 148
Google Scholar
[18] Copley S M, Giamei A F, Johnson S M, Hornbecker M F 1970 Metall. Trans. 1 2193
Google Scholar
[19] Basu A J, Khalili A 1999 Phys. Fluids 11 1395
Google Scholar
[20] Shen C J, Jin G Q, Xin P, Kong J, Li L 2015 Water Resour. Res. 51 4301
Google Scholar
[21] Beavers G S, Joseph D D 1967 J. Fluid Mech. 30 11
Google Scholar
[22] Kuznetsov A V 1997 Int. Commun. Heat Mass Transfer 24 401
Google Scholar
[23] 娄钦, 黄一帆, 李凌 2019 68 214702
Google Scholar
Lou Q, Huang Y, Li L 2019 Acta Phys. Sin. 68 214702
Google Scholar
[24] Caltagirone J P 1975 J. Fluid Mech. 72 269
Google Scholar
[25] Zhan J M, Luo Y Y, Li Y S 2008 Appl. Math. Modell. 32 873
Google Scholar
[26] Zhang X F, Wang L L, Lin C, Zhu H, Zeng C 2018 Phys. Fluids 30 022110
Google Scholar
[27] Garaud P 2018 Annu. Rev. Fluid Mech. 50 275
Google Scholar
[28] Kunze E 1987 J. Mar. Res. 45 533
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6531
- PDF Downloads: 68
- Cited By: 0
