-
Dry granular materials are composed of a dense random packing of macroscopic grains. As a small amount of liquid is added to granular samples, the liquid bridge forces, i.e. the forces between liquid and the grains, have an influence on the mechanical properties of wet granular material, and some of these properties are quite different from those of dry granular materials. In this work, by measuring the acceleration of the sample chamber and the force exerted on it by the shaker, the variations of bulk modulus and energy dissipation of both dry and wet glass bead samples with pressure and viscosity under vertical vibration are studied. The results are shown below. 1) Under low saturation, the bulk modulus of dry and wet glass bead sample are both described by a power law scaling law with pressure, which is close to the power law relationship predicted by the efficient medium theory on the basis of Hertz contact potential. A small amount of liquid can increase the bulk modulus of glass bead sample. At the same pressure and liquid content, the bulk modulus of wet glass bead sample increases with liquid viscosity increasing. Based on Hertzian contact mechanics, an efficient elastic network model is proposed to illustrate the mechanism of increasing bulk modulus of wet glass bead samples. 2) The energy dissipation of dry and wet glass bead sample decrease following the power law of pressure, and the energy dissipation of wet glass bead samples is proportional to the kinematic viscosity of liquid. 3) With the increase of strain amplitude, the softening behavior of the wet glass bead sample is similar to that of the dry glass bead sample, when the strain amplitude is higher than the strain threshold value. The kinematic viscosity of liquid inhibits the softening behavior of glass bead sample.
-
Keywords:
- granular materials /
- bulk modulus /
- energy dissipation /
- capillary forces
[1] Makse H A, Gland N, Johnson D L, Schwartz L 2004 Phys. Rev. E 70 061302
Google Scholar
[2] Lemrich L, Carmeliet J, Johnson P A 2017 Phys. Rev. E 96 062901
Google Scholar
[3] Somfai E, Roux J N, Snoeijer J H 2005 Phys. Rev. E 72 021301
Google Scholar
[4] Zimmer M A, Prasad M, Mavko G, Nur A 2007 Geophysics 72 E1
Google Scholar
[5] Zimmer M A, Prasad M, Mavko G, Nur A 2007 Geophysics 72 E15
Google Scholar
[6] Badetti M, Fall A, Hautemayou D 2018 J. Rheol. 62 1175
Google Scholar
[7] 唐瀚玉, 王娜, 吴学邦 2018 67 206402
Google Scholar
Tang H Y, Wang N, Wu X B 2018 Acta Phys. Sin. 67 206402
Google Scholar
[8] Fall A, Weber B, Pakpour M 2014 Phys. Rev. Lett. 112 175502
Google Scholar
[9] Wang W J, Zhu Z G 2008 EPL 82 24004
Google Scholar
[10] Brunet T, Jia X, Mills P 2008 Phys. Rev. Lett. 101 138001
Google Scholar
[11] Kovalcinova L, Karmakar S, Schaber M 2018 Phys. Rev. E 98 032905
Google Scholar
[12] Johnson P A, Jia X 2005 Nature 437 871
Google Scholar
[13] Reichhardt C J O, Lopatina L M, Jia X, Johnson P A 2015 Phys. Rev. E 92 022203
Google Scholar
[14] Brum J, Gennisson J L, Fink M 2019 Phys. Rev. E 99 042902
Google Scholar
[15] Griffiths S, Rescaglio A, Melo F 2010 Ultrasonics 50 139
Google Scholar
[16] Liao C C, Hsiau S S 2010 Powder Technol. 197 222
Google Scholar
[17] Fournier Z, Geromichalos D, Herminghaus S 2005 J. Phys. Condens. Matter 17 S477
Google Scholar
[18] Pilbeam C C, Vaišnys J R 1973 J. Geophys. Res. 78 810
Google Scholar
[19] Liu X, Greenhalgh S, Zhou B 2018 Geophys. J. Int. 212 1255
Google Scholar
[20] Li D, Wei J, Di B 2017 J. Geophys. Eng. 14 1072
Google Scholar
[21] Fawad M, Mondol N H, Jahren J 2011 Geophys. Prospect. 59 697
Google Scholar
[22] Tittmann B, Abdel-Gawad M, Salvado C 1981 Proc. Lunar Planet. Sci. 12B 1737
[23] Aliasgari M, Maleki-Jirsaraei N, Rouhani S 2021 EPJ Web Conf. 249 08003
Google Scholar
[24] Tong L H, Qi B, Ding H 2020 Int. J. Mech. Sci. 171 105373
Google Scholar
-
图 1 (a)实验装置示意图; (b)湿颗粒体系中的液桥形态示意图
Figure 1. (a) Schematic diagram of the experimental device; (b) pendular bridges in wet glass bead sample.
图 2 频率
$ f = 300\;{\text{Hz}} $ 、位移幅值$ A = 565\;{\text{nm}} $ 的正弦加速度信号(a)及其频谱图(b)Figure 2. (a) Sinusoidal acceleration signal with frequency
$ f = 300\;{\text{Hz}} $ and displacement amplitude$ A = 565\;{\text{nm}} $ and (b) its spectrum diagram.
图 3 不同运动黏度
$ {\nu _{{\text{lig}}}} $ 下, 玻璃珠样品的体积模量K随压强p的变化(液体含量$ w = 1 $ %)Figure 3. Variation of bulk modulus K of glass bead samples with pressure p under different kinematic viscosity
$ {\nu _{{\text{lig}}}} $ (liquid content$ w = 1 $ %).
图 4 不同压强 p下, 湿玻璃珠样品的体积模量K随运动黏度
$ {\nu _{{\text{lig}}}} $ 的变化(液体含量$ w = 1 $ %)Figure 4. Variation of bulk modulus K with kinematic viscosity
$ {\nu _{{\text{lig}}}} $ under different pressure p (liquid content$ w = 1 $ %).
图 5 不同运动黏度
$ {\nu _{{\text{lig}}}} $ 下, 玻璃珠样品相对能耗$ \tan \phi $ 随压强 p 的变化(液体含量$ w = 1 $ %)Figure 5. Variation of relative energy dissipation
$ \tan \phi $ with pressure p under different kinematic viscosity (liquid content$ w = 1 $ %).
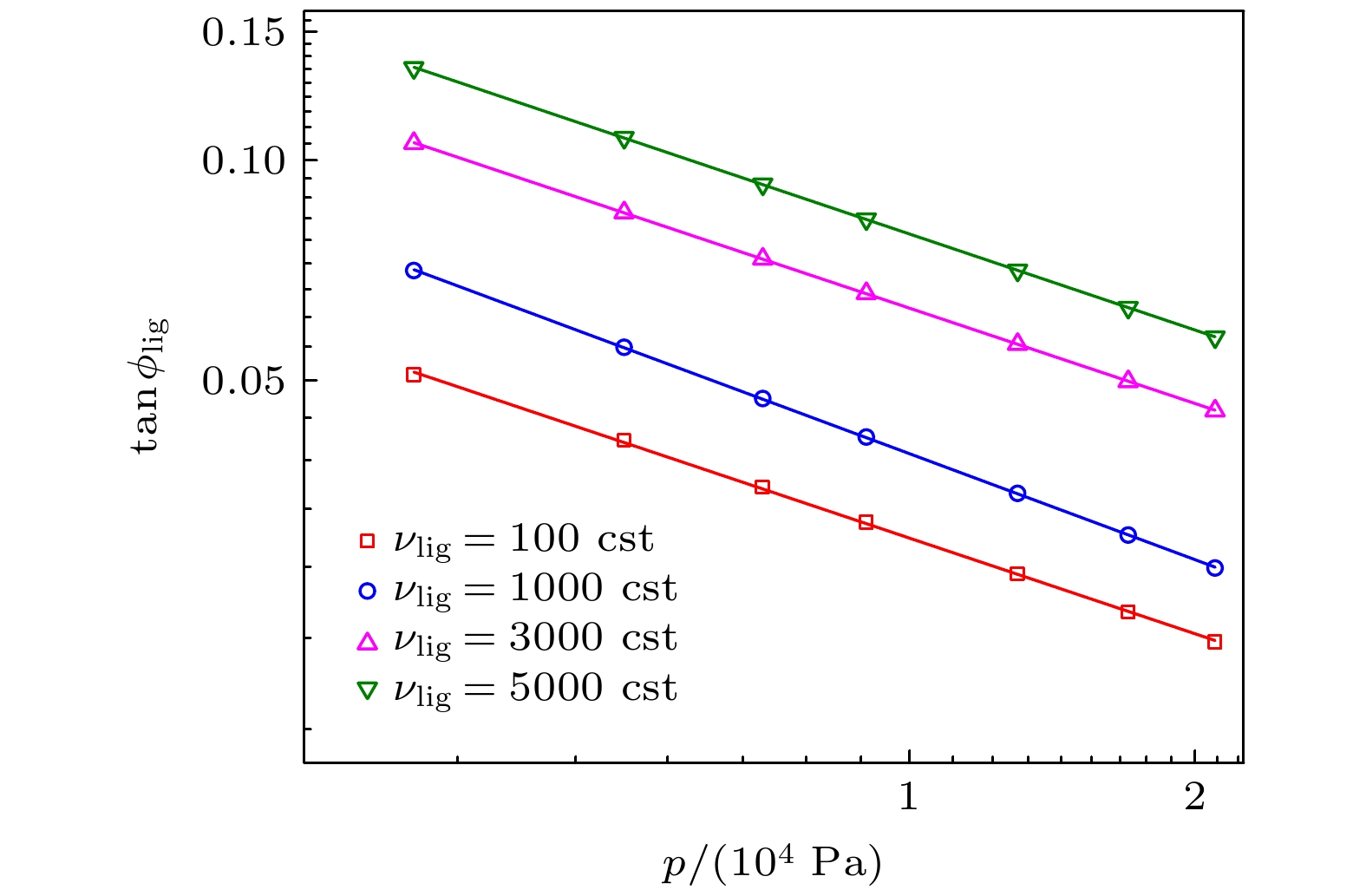
图 6 不同运动黏度
$ {\nu _{{\text{lig}}}} $ 下, 湿玻璃珠样品液桥的断裂和形成而产生的相对能耗$ \tan {\phi _{{\text{lig}}}} $ 随压强 p 的变化(液体含量$ w = 1 $ %)Figure 6. Variation of relative energy dissipation by rupture and reformation of the capillary bridges
$ \tan {\phi _{{\text{lig}}}} $ with pressure p under different kinematic viscosity$ {\nu _{{\text{lig}}}} $ (liquid content$ w = 1 $ %).
图 7 不同压强p下, 湿玻璃珠样品的相对能耗
$ \tan \phi $ 随运动黏度$ {\nu _{{\text{lig}}}} $ 的变化(液体含量$ w = 1$ %)Figure 7. Variation of relative energy dissipation
$ \tan \phi $ with kinematic viscosity$ {\nu _{{\text{lig}}}} $ under different pressure p (liquid content$ w = 1 $ %).
图 8 不同运动黏度
$ {\nu _{{\text{lig}}}} $ 下, 玻璃珠样品的归一化体积模量变化${\Delta K}/K_0$ 随应变幅值$ \varepsilon $ 的变化(液体含量$ w = 1 $ %). 虚线对应近似的应变阈值, 即当应变幅值低于阈值时, 系统动态响应是线性的,${{{\Delta K}/K}_0} = 0$ , 与振幅无关; 在高应变幅值下,${{{\Delta K}/K}_0} < 0$ , 材料软化Figure 8. Variation of the normalized bulk modulus change
$ {{\Delta K} \mathord{\left/ {\vphantom {{\Delta K} {{K_0}}}} \right. } {{K_0}}} $ with strain amplitude$ \varepsilon $ under different kinematic viscosity$ {\nu _{{\text{lig}}}} $ (liquid content$ w = 1 $ %). The dashed line indicates that there is an approximate strain threshold, when the strain amplitude is lower than the threshold value, the dynamic response of the system is linear,${\Delta K}/K_0 = 0$ , and independent of the amplitude. At high strain amplitude,${{{\Delta K}/K}_0} < 0$ , the system is softened.表 1 不同运动黏度下, 玻璃珠样品体积模量和相对耗散随压强变化的幂指数
Table 1. Power law exponents of bulk modulus and energy dissipation with pressure and kinematic viscosity.
运动黏度$ {\nu _{{\text{lig}}}} $/cst 0 100 1000 3000 5000 体积模量随压强
变化的幂指数a0.396 0.370 0.346 0.333 0.327 相对耗散随压强
变化的幂指数b–0.327 –0.395 –0.429 –0.407 –0.415 
DownLoad: CSV
-
[1] Makse H A, Gland N, Johnson D L, Schwartz L 2004 Phys. Rev. E 70 061302
Google Scholar
[2] Lemrich L, Carmeliet J, Johnson P A 2017 Phys. Rev. E 96 062901
Google Scholar
[3] Somfai E, Roux J N, Snoeijer J H 2005 Phys. Rev. E 72 021301
Google Scholar
[4] Zimmer M A, Prasad M, Mavko G, Nur A 2007 Geophysics 72 E1
Google Scholar
[5] Zimmer M A, Prasad M, Mavko G, Nur A 2007 Geophysics 72 E15
Google Scholar
[6] Badetti M, Fall A, Hautemayou D 2018 J. Rheol. 62 1175
Google Scholar
[7] 唐瀚玉, 王娜, 吴学邦 2018 67 206402
Google Scholar
Tang H Y, Wang N, Wu X B 2018 Acta Phys. Sin. 67 206402
Google Scholar
[8] Fall A, Weber B, Pakpour M 2014 Phys. Rev. Lett. 112 175502
Google Scholar
[9] Wang W J, Zhu Z G 2008 EPL 82 24004
Google Scholar
[10] Brunet T, Jia X, Mills P 2008 Phys. Rev. Lett. 101 138001
Google Scholar
[11] Kovalcinova L, Karmakar S, Schaber M 2018 Phys. Rev. E 98 032905
Google Scholar
[12] Johnson P A, Jia X 2005 Nature 437 871
Google Scholar
[13] Reichhardt C J O, Lopatina L M, Jia X, Johnson P A 2015 Phys. Rev. E 92 022203
Google Scholar
[14] Brum J, Gennisson J L, Fink M 2019 Phys. Rev. E 99 042902
Google Scholar
[15] Griffiths S, Rescaglio A, Melo F 2010 Ultrasonics 50 139
Google Scholar
[16] Liao C C, Hsiau S S 2010 Powder Technol. 197 222
Google Scholar
[17] Fournier Z, Geromichalos D, Herminghaus S 2005 J. Phys. Condens. Matter 17 S477
Google Scholar
[18] Pilbeam C C, Vaišnys J R 1973 J. Geophys. Res. 78 810
Google Scholar
[19] Liu X, Greenhalgh S, Zhou B 2018 Geophys. J. Int. 212 1255
Google Scholar
[20] Li D, Wei J, Di B 2017 J. Geophys. Eng. 14 1072
Google Scholar
[21] Fawad M, Mondol N H, Jahren J 2011 Geophys. Prospect. 59 697
Google Scholar
[22] Tittmann B, Abdel-Gawad M, Salvado C 1981 Proc. Lunar Planet. Sci. 12B 1737
[23] Aliasgari M, Maleki-Jirsaraei N, Rouhani S 2021 EPJ Web Conf. 249 08003
Google Scholar
[24] Tong L H, Qi B, Ding H 2020 Int. J. Mech. Sci. 171 105373
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3142
- PDF Downloads: 47
- Cited By: 0
