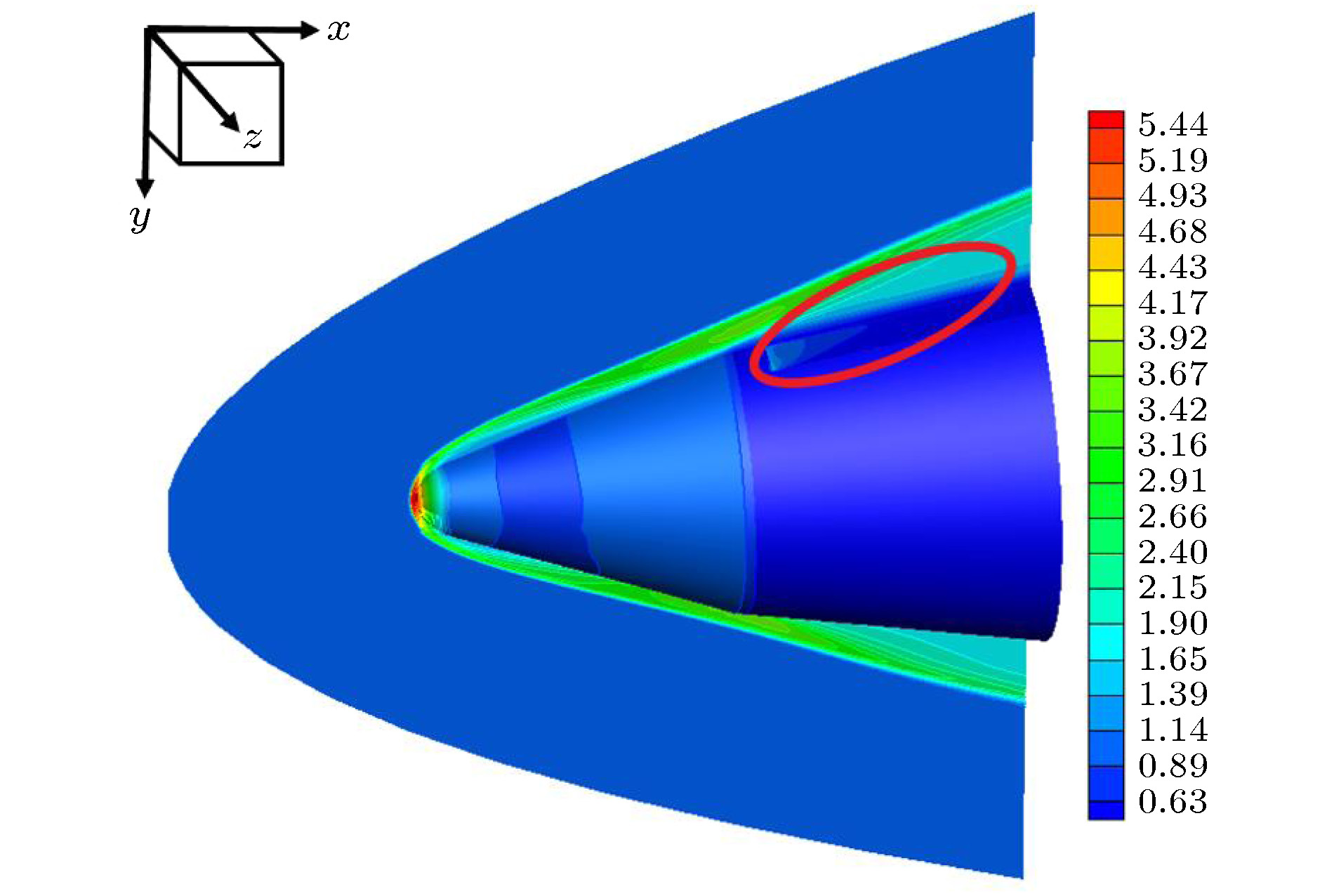
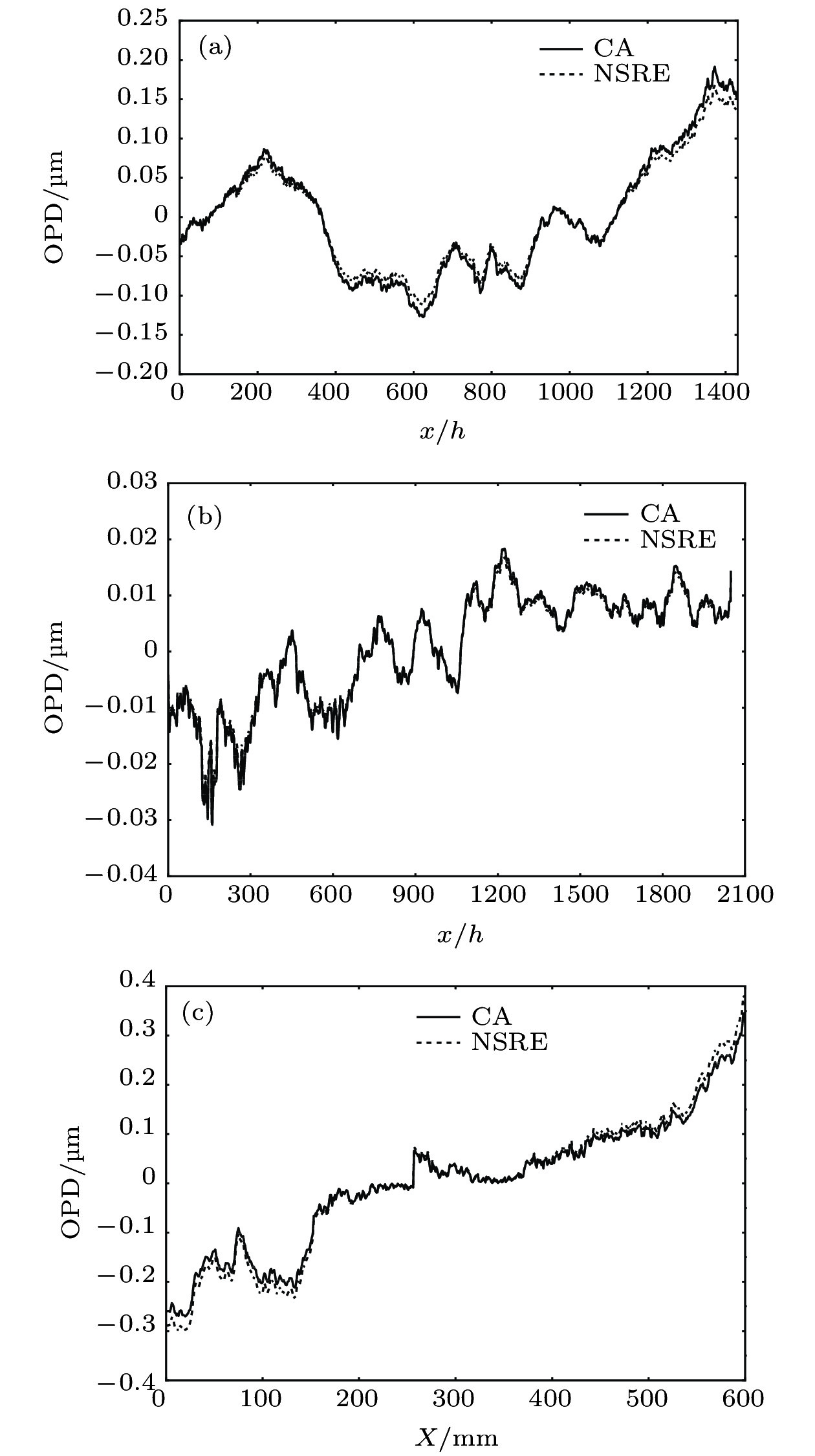
-
For the supersonic flow field with large density fluctuation produced by the unsteady flow and turbulent large-scale structures, an effective method to obtain the beam path is to solve the ray equation. Then the optical path difference (OPD), Strehl ratio (SR), optical transmission function (OTF), etc. can be obtained to analyze the optical distortion, and the correction of aero optics effects can be realized to improve the optical system performance. Generally, when the refractive index distribution is arbitrary, the ray equation analytic solution is difficult to obtain. Cellular automata (CA) ray tracing algorithm is proposed in this paper for aero-optical calculation in the 2D discrete flow fields. Unlike numerically solving the ray equation (NSRE), the coordinate value and the offset angle are calculated according to the position and direction transformation rules in CA algorithm. The position transformation rule is used to obtain the end point of the beam vector and determine whether the offset angle needs calculating at each iteration, the direction transformation rule is to calculate the offset angles. Then the refractive index field is integrated along the beam path to obtain the optical path length (OPL). The OPD is calculated from OPL. In this paper, aero-optical calculation is based on two types of flow fields. The supersonic shear layer including supersonic mixing layer and boundary layer 2D density distribution is measured by the nano-tracer-based planar laser scattering (NPLS) technique. The supersonic flow field surrounding the optical dome is simulated based on detached-eddy simulation (DES). The OPDrms and program running time quantitatively verify the calculation accuracy and high efficiency of CA. The results show that for the 2D supersonic NPLS flow field and the 2D supersonic flow field surrounding the optical dome, the calculation accuracy of CA is approximately equal to NSRE. Moreover, we find that the program running time of NSRE is about four times that of the CA algorithm, so the efficiency of ray tracing is effectively improved. Thus, the CA algorithm provides a new scheme for aero-optical calculation in the 2D supersonic flow field. Meanwhile, it also provides a guideline for the research on the ray tracing in 3D discrete aero-optical flow field. -
Keywords:
- aero optics /
- cellular automata /
- ray tracing /
- optical path difference
[1] Gordeyev S, Jumper E 2010 Prog. Aerosp. Sci. 46 8
[2] 谢文科, 刘俊圣, 费家乐, 周全, 夏辉, 陈欣, 张盼, 彭一鸣, 于涛 2019 68 094202
Google Scholar
Xie W K, Liu J S, Fei J L, Zhou Q, Xia H, Chen X, Zhang P, Peng Y M, Yu T 2019 Acta Phys. Sin. 68 094202
Google Scholar
[3] Pond J E, Sutton G W 2006 J. Aircraft 43 3
[4] Ding H L, Yi S H, Zhu Y Z, He L 2017 Appl. Opt. 56 27
Google Scholar
[5] 于涛, 夏辉, 樊志华, 谢文科, 张盼, 刘俊圣, 陈欣 2018 67 134203
Google Scholar
Yu T, Xia H, Fan Z H, Xie W K, Zhang P, Liu J S, Chen X 2018 Acta Phys. Sin. 67 134203
Google Scholar
[6] Zhu K C, Li S X, Tang Y, Yu Y, Tang H Q 2012 J. Opt. Soc. Am. A 29 3
[7] Montagnino L 1968 J. Opt. Soc. Am. A 58 12
[8] Chang X F, Wang T, Wan S Z, Yan J, Fu W X 2015 Optik 126 23
[9] Xu L, Xue D T, Lv X Y 2018 Opt. Express 26 1
Google Scholar
[10] Tang L P, Tang L M , Wang D, Deng H X, Chen K Q 2018 J. Phys.: Condens. Matter 30 465301
[11] Chen Q, Wang Y 2015 Physica A 432 15
[12] Sun G Q, Jin Z, Song L P, Chakraborty A, Li B L 2011 Ecol. Res. 26 2
[13] Chen C K, Li J, Zhang D 2012 Physica A 391 7
[14] Ahmadpour S S, Mosleh M 2018 J. Supercomput. 74 9
[15] Qin Y, Feng M Y, Lu H C, Cottrell G W 2018 Int. J. Comput. Vision. 126 751
Google Scholar
[16] Zhang H, Wei J, Gao X L, Hu J 2019 Int. J. Mod. Phys. C 30 5
[17] 朱杨柱, 易仕和, 孔小平, 全鹏程, 陈植, 田立丰 2014 63 134701
Google Scholar
Zhu Y Z, Yi S H, Kong X P, Quan P C, Chen Z, Tian L F 2014 Acta Phys. Sin. 63 134701
Google Scholar
[18] Yi S H, He L, Zhao Y X, Tian L F, Cheng Z Y 2009 Sci. China, Ser. G 52 12
Google Scholar
[19] Zhu J, Li X L, Tang H Q, Zhu K C 2017 Opt. Express 25 17
Google Scholar
[20] Yu T, Xia H, Fan Z H, Xie W K, Zhang P, Liu J S, Chen X, Chu X X 2018 Opt. Commun. 436 1
Google Scholar
[21] Guo G M, Liu H 2017 Appl. Opt. 56 16
Google Scholar
[22] Ji B, Long Y, Long X P, Qian Z D, Zhou J J 2017 J. Hydrodyn. 29 1
Google Scholar
[23] Weghorst H, Hooper G, Greenberg D P 1984 Acm. T. Graphic. 3 1
Google Scholar
[24] Huang Y, Shi G D, Zhu K Y 2016 J. Quant. Spectrosc. Radiat. 176 24
Google Scholar
[25] Jiang H, Ren G, Zheng L, Cheng J X, Huang Z F 2014 Int. J. Mod. Phys. B 28 16
[26] 赵玉新 2008 博士学位论文(长沙: 国防科学技术大学)
Zhao Y X 2008 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[27] 易仕和, 赵玉新, 田立丰, 何霖, 程忠宇 2009 空气动力学学报 27 114
Google Scholar
Yi S H, Zhao Y X, Tian L F, He L, Cheng Z Y 2009 Acta Aerodyn. Sin. 27 114
Google Scholar
[28] 易仕和, 陈植, 何霖, 武宇, 田立丰 2014 实验流体力学 28 1
Google Scholar
Yi S H, Chen Z, He L, Wu Y, Tian L F 2014 J. Fluid. Mech. 28 1
Google Scholar
[29] Tian L F, Yi S H, Zhao Y X, He L, Chen Z Y 2009 Sci. China, Ser. G 52 9
Google Scholar
[30] Lyons D C, Peltier L J, Zajaczkowski F J, Paterson E G 2007 J. Fluids Eng.-Trans. ASME 131 11
[31] Usta O, Korkut E 2018 Ocean Eng. 160 15
Google Scholar
-
图 1 NPLS获得的超声速剪切层图像 (a)混合层; (b)边界层
Figure 1. The flow visualization results of supersonic shear layers obtained by NPLS: (a) Supersonic mixing layer; (b) supersonic boundary layer.
图 2 光学头罩绕流流场密度场
Figure 2. The density field distribution of supersonic flow field surrounding the optical dome obtained by DES.
图 3 CA算法与NSER算法在混合层得的光线路径
Figure 3. Beam paths obtained by CA and NSRE in mixing layer.
图 4 CA算法与NSRE算法计算得到的OPD (a)混合层; (b)边界层; (c)含激波的超声速光学头罩二维剖面流场
Figure 4. The OPD results calculated by CA and NSRE: (a) Supersonic mixing layer; (b) supersonic boundary layer; (c) supersonic flow field surrounding the optical dome.
表 1 CA与NSRE算法计算混合层流场的程序执行时间
Table 1. The program running time of CA and NSRE in mixing layer.
方法 t1/s t2/s t3/s t4/s t5/s ta/s CA 2.032 2.041 2.157 2.085 2.077 2.078 NSRE 8.463 8.470 8.522 8.491 8.511 8.491 
DownLoad: CSV
表 2 CA与NSRE算法计算边界层流场的程序执行时间
Table 2. The program running time of CA and NSRE in boundary layer.
方法 t1/s t2/s t3/s t4/s t5/s ta/s CA 1.966 2.002 1.983 1.964 1.972 1.977 NSRE 7.241 7.250 7.143 7.250 7.219 7.220
DownLoad: CSV
表 3 CA与NSRE算法计算高速绕流流场的程序执行时间
Table 3. The program running time of CA and NSRE in supersonic flow field surrounding the optical dome.
方法 t1/s t2/s t3/s t4/s t5/s ta/s CA 2.831 2.884 2.827 2.873 2.840 2.851 NSRE 11.375 11.525 11.401 11.380 11.397 11.416
DownLoad: CSV
-
[1] Gordeyev S, Jumper E 2010 Prog. Aerosp. Sci. 46 8
[2] 谢文科, 刘俊圣, 费家乐, 周全, 夏辉, 陈欣, 张盼, 彭一鸣, 于涛 2019 68 094202
Google Scholar
Xie W K, Liu J S, Fei J L, Zhou Q, Xia H, Chen X, Zhang P, Peng Y M, Yu T 2019 Acta Phys. Sin. 68 094202
Google Scholar
[3] Pond J E, Sutton G W 2006 J. Aircraft 43 3
[4] Ding H L, Yi S H, Zhu Y Z, He L 2017 Appl. Opt. 56 27
Google Scholar
[5] 于涛, 夏辉, 樊志华, 谢文科, 张盼, 刘俊圣, 陈欣 2018 67 134203
Google Scholar
Yu T, Xia H, Fan Z H, Xie W K, Zhang P, Liu J S, Chen X 2018 Acta Phys. Sin. 67 134203
Google Scholar
[6] Zhu K C, Li S X, Tang Y, Yu Y, Tang H Q 2012 J. Opt. Soc. Am. A 29 3
[7] Montagnino L 1968 J. Opt. Soc. Am. A 58 12
[8] Chang X F, Wang T, Wan S Z, Yan J, Fu W X 2015 Optik 126 23
[9] Xu L, Xue D T, Lv X Y 2018 Opt. Express 26 1
Google Scholar
[10] Tang L P, Tang L M , Wang D, Deng H X, Chen K Q 2018 J. Phys.: Condens. Matter 30 465301
[11] Chen Q, Wang Y 2015 Physica A 432 15
[12] Sun G Q, Jin Z, Song L P, Chakraborty A, Li B L 2011 Ecol. Res. 26 2
[13] Chen C K, Li J, Zhang D 2012 Physica A 391 7
[14] Ahmadpour S S, Mosleh M 2018 J. Supercomput. 74 9
[15] Qin Y, Feng M Y, Lu H C, Cottrell G W 2018 Int. J. Comput. Vision. 126 751
Google Scholar
[16] Zhang H, Wei J, Gao X L, Hu J 2019 Int. J. Mod. Phys. C 30 5
[17] 朱杨柱, 易仕和, 孔小平, 全鹏程, 陈植, 田立丰 2014 63 134701
Google Scholar
Zhu Y Z, Yi S H, Kong X P, Quan P C, Chen Z, Tian L F 2014 Acta Phys. Sin. 63 134701
Google Scholar
[18] Yi S H, He L, Zhao Y X, Tian L F, Cheng Z Y 2009 Sci. China, Ser. G 52 12
Google Scholar
[19] Zhu J, Li X L, Tang H Q, Zhu K C 2017 Opt. Express 25 17
Google Scholar
[20] Yu T, Xia H, Fan Z H, Xie W K, Zhang P, Liu J S, Chen X, Chu X X 2018 Opt. Commun. 436 1
Google Scholar
[21] Guo G M, Liu H 2017 Appl. Opt. 56 16
Google Scholar
[22] Ji B, Long Y, Long X P, Qian Z D, Zhou J J 2017 J. Hydrodyn. 29 1
Google Scholar
[23] Weghorst H, Hooper G, Greenberg D P 1984 Acm. T. Graphic. 3 1
Google Scholar
[24] Huang Y, Shi G D, Zhu K Y 2016 J. Quant. Spectrosc. Radiat. 176 24
Google Scholar
[25] Jiang H, Ren G, Zheng L, Cheng J X, Huang Z F 2014 Int. J. Mod. Phys. B 28 16
[26] 赵玉新 2008 博士学位论文(长沙: 国防科学技术大学)
Zhao Y X 2008 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[27] 易仕和, 赵玉新, 田立丰, 何霖, 程忠宇 2009 空气动力学学报 27 114
Google Scholar
Yi S H, Zhao Y X, Tian L F, He L, Cheng Z Y 2009 Acta Aerodyn. Sin. 27 114
Google Scholar
[28] 易仕和, 陈植, 何霖, 武宇, 田立丰 2014 实验流体力学 28 1
Google Scholar
Yi S H, Chen Z, He L, Wu Y, Tian L F 2014 J. Fluid. Mech. 28 1
Google Scholar
[29] Tian L F, Yi S H, Zhao Y X, He L, Chen Z Y 2009 Sci. China, Ser. G 52 9
Google Scholar
[30] Lyons D C, Peltier L J, Zajaczkowski F J, Paterson E G 2007 J. Fluids Eng.-Trans. ASME 131 11
[31] Usta O, Korkut E 2018 Ocean Eng. 160 15
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6311
- PDF Downloads: 146
- Cited By: 0
