-
Ray tracing plays a key role in lens design area, and it is an important tool to study the problems in physics like optics. Nowadays, ray tracing becomes ubiquitous and is widely used in optical automatic design, such as aberration analysis, optimization, and tolerance calculation. With the impulse of application requirements, optical systems like space camera develop towards large scale, high degree of accuracy and complication. The magnitude of aberrations increases exponentially with the growth of focal length and aperture, even a minor perturbation error can result in severe degeneration of image quality. As a consequence, the stringent requirements for precision, accuracy and stability of ray tracing turn higher. Reliable commercial software, for example, America’s Zemax, has high precision in ray tracing, because of commercial purpose, the process of ray tracing is a black box. It is now more important to understand what error factors are formed for ray tracing, and how these running errors can be reduced effectively. In this paper, from floating point arithmetic perspective, an error model for ray tracing is provided. This error model is suitable for not only meridional rays, but also skew rays. Starting from IEEE Standard for Binary Floating-Point Arithmetic, presentation error and rounding error are analyzed, followed by the computation process of ray’s intersection point with a quadratic surface, then rounding error expression for the intersection point is presented. In addition, error expression for distance along the ray from the reference surface to the next surface is also induced. These two error expressions are called error model, and it clearly indicates that spatial coordinates on the reference surface, direction vector and distance between the two adjacent surfaces are the main error sources. Based on the error model, some of effective measures, for instance, reprojection, spatial transformation, and direction vector’s normalization are taken to reduce the rounding error. Moreover, in the process of solving quadratic equation, conjugate number method is utilized in order to avoid increasing substantially in relative error called catastrophic cancellation. Numerical experiments and classical optical design for space camera are also given. From numerical computing view, two precision tests based on Multiple Precision Floating-Point Reliable (MPFR) library are introduced to verify our method mathematically. The experimental results show that our algorithm has the same precision (14 significant digits) as MPFR, while the existing method fails to pass tests, and has only 8 significant digits at most. Moreover, both the Cassegrain space camera and off-axis three-mirror-anastigmat space camera are used to illustrate our method’s accuracy. Experimental results indicate that our method has higher precision, more than 5 to 6 orders of magnitudes than the existing method. In addition, our algorithm has higher precision than the commercial optical design software Zemax, and residuals are 3 orders of magnitudes on average less than Zemax.
-
Keywords:
- ray tracing /
- error model /
- numerical algorithm /
- optical design /
- space camera
[1] 郭疆, 朱磊, 赵继, 龚大鹏 2021 光学精密工程 27 1138
Google Scholar
Guo J, Zhu L, Zhao J, Gong D P 2021 Opt. Precision Eng. 27 1138
Google Scholar
[2] 高洋, 王书新, 齐光, 孙斌, 伞兵, 李景林 2022 光学技术 48 562
Google Scholar
Gao Y, Wang S X, Qi G, Sun B, San B, Li J L 2022 Opt. Techn. 48 562
Google Scholar
[3] 孟庆宇, 汪洪源, 王维, 秦子长, 王晓东 2021 光学精密工程 29 72
Google Scholar
Meng Q Y, Wang H Y, Wang W, Qin Z C, Wang X D 2021 Opt. Precision Eng. 29 72
Google Scholar
[4] Zhong C L, Sang X Z, Yan B B, Li H, Chen D, Qin X J 2022 Opt. Express 30 40087
Google Scholar
[5] [6] Whitted T 1980 Commun. ACM 23 6
[7] Veach E 1997 Ph. D. Dissertation (Stanford: Stanford University)
[8] Braddick H J J 1960 Rep. Prog. Phys. 23 154
Google Scholar
[9] 王之江 1985 光学设计理论基础 (第二版) (北京: 科学出版社) 第3—36 页
Wang Z J 1985 Fundamental Theory of Lens Design (2nd Ed.) (Beijing: Science Press) pp3–36 (in Chinese)
[10] 王涌天 1990 光学技术 5 2
Wang Y T 1990 Opt. Techn. 5 2
[11] 李林, 安连生 2002 计算机辅助光学设计的理论与应用 (北京: 国防工业出版社) 第1—38 页
Li L, An L S 2002 Theory and Application of Computer Aided Optical Design (Beijing: National Defense Industry Press) pp1–38 (in Chinese)
[12] 李晓彤, 岑兆丰 2021 几何光学·像差·光学设计 (第4 版) (杭州: 浙江大学出版社) 第162—179 页
Li X T, Cen Z F 2021 Geometrical Optics, Aberrations and Optical Design (4th Ed.) (Hangzhou: Zhejiang University Press) pp162–179 (in Chinese)
[13] 张以谟, 张红霞, 贾大功 2021 应用光学 (第5版) (北京: 电子工业出版社) 第14—21 页
Zhang Y M, Zhang H X, Jia D G 2021 Applied Optics (5th Ed.) (Beijing: Publishing House of Electronics Industry) pp14–21(in Chinese)
[14] Marrs A, Shirley P, Wald I 2021 Ray Tracing Gems Ⅱ: Next Generation Real-Time Rendering with DXR, Vulkan, and OptiX (1st Ed.) (New York: Apress) pp545–550
[15] 步志超, 张淳民, 赵葆常, 朱化春 2009 58 2415
Google Scholar
Bu Z C, Zhang C M, Zhu H C 2009 Acta Phys. Sin. 58 2415
Google Scholar
[16] Spence S E, Parks A D 2016 Appl. Opt. 55 C46
Google Scholar
[17] 王楠, 阮双琛 2020 69 024201
Google Scholar
Wang N, Ruan S C 2020 Acta Phys. Sin. 69 024201
Google Scholar
[18] Schedin S, Hallberg P, Behndig A 2017 Appl. Opt. 56 9787
Google Scholar
[19] Ferrer-Rodríguez J P, Saura J M, Fernández E F, Almonacid F, Talavera D L, Pérez-Higueras P 2020 Opt. Express 28 6609
Google Scholar
[20] Huang F, Ren H, Shen Y, Wang P F 2021 Appl. Opt. 60 2574
Google Scholar
[21] Sun Q L, Wang C L, Fu Q, Dun X, Heidrich W 2021 ACM Trans. Graph. 40 71
Google Scholar
[22] Halé A, Trouvé-Peloux P, Volatier J B 2021 Opt. Express 29 34748
Google Scholar
[23] Liu A Q, Su L J, Yuan Y, Ding X M 2020 Opt. Express 28 2251
Google Scholar
[24] Marschner S, Shirley P 2022 Fundamentals of Computer Graphics (5th Ed.) (New York: CRC Press) pp80–95
[25] Higham N J 2002 Accuracy and Stability of Numerical Algorithms (2nd Ed.) (Philadelphia: SIAM) pp35–60
[26] Fousse L, Hanrot G, Lefèvre V, Pélissier P, Zimmermann P 2007 ACM Trans. Math. Softw. 33 13
Google Scholar
-
图 5 几何计算与MPFR结合验证光线追迹精度
Fig. 5. Verification of ray tracing precision combining geometric computing and MPFR
图 6 MPFR四精度浮点数标准点
Fig. 6. MPFR's quadruple precision floating-point numbers on unit sphere
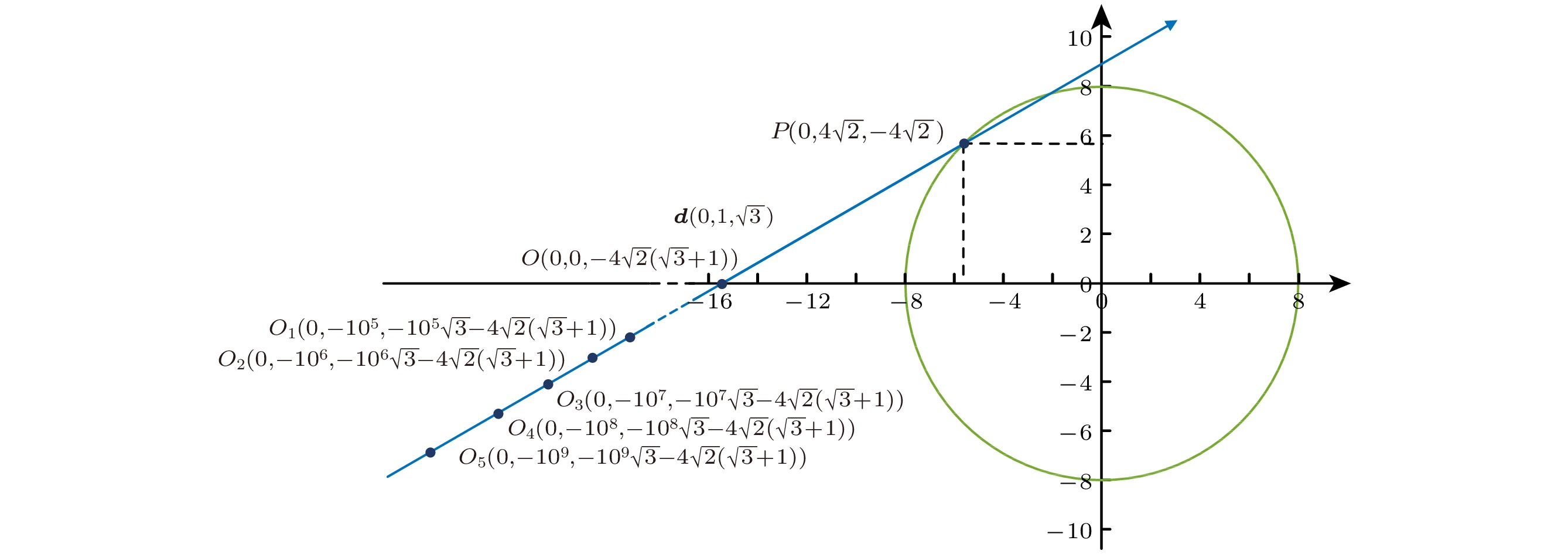
表 1 光线始点对光线追迹结果的影响
Table 1. Results of ray tracing algorithm with different ray original points
光线始点 算法类别 交点$ P $坐标 残差$ |F(P_x, P_y, P_z)| $ $ P_x $ $ P_y $ $ P_z $ $ O(0, 0, -4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-13} $ 原有方法 0 5.65685425535717 –5.65685423933425 3.04772385106844$ \times 10^{-9} $ $ O_1(0, -10^5, -10^5\sqrt{3}-4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-15} $ 原有方法 0 5.65685252461116 –5.65685719583416 1.38192605021459$ \times 10^{-5} $ $ O_2(0, -10^6, -10^6\sqrt{3}-4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-13} $ 原有方法 0 5.65709940693341 –5.65642958320677 2.03067029689663$ \times 10^{-3} $ $ O_3(0, -10^7, -10^76\sqrt{3}-4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-13} $ 原有方法 0 5.66135398671031 –5.64906043559312 3.71872321756541$ \times 10^{-2} $ $ O_4(0, -10^8, -10^8\sqrt{3}-4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-13} $ 原有方法 0 6.69213041663169 –3.86370331048965 4.28718721530413$ \times 10^{0} $ $ O_5(0, -10^9, -10^9\sqrt{3}-4\sqrt{2}(\sqrt{3}+1) $ MPFR 0 5.65685424949238 –5.65685424949238 1.42108547152020$ \times 10^{-14} $ 本文方法 0 5.65685424949238 –5.65685424949237 1.27897692436818$ \times 10^{-13} $ 原有方法 0 –15.9352867603302 –43.0555386543273 2.04371277294824$ \times 10^{3} $ 
下载: 导出CSV
表 2 不同光线追迹方法结果
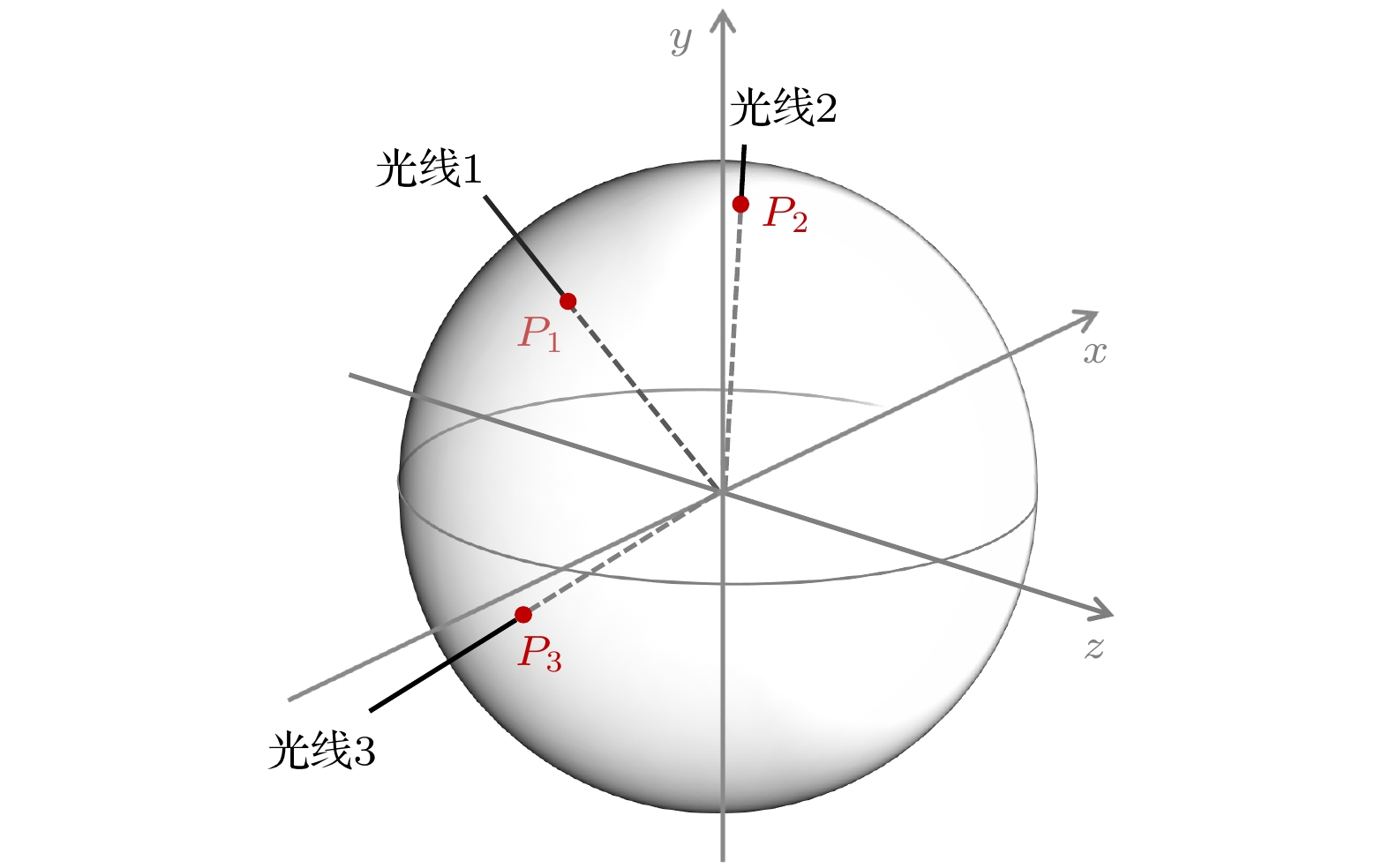
Table 2. Results of different ray tracing algorithms
光线编号 算法类别 交点$ P $坐标 残差$ |F(P_x, P_y, P_z)| $ $ P_x $ $ P_y $ $ P_z $ 1 MPFR 0.379693092393262 0.541344968359402 –0.750185830858461 3.33066907387547$ \times 10^{-16} $ 本文方法 0.379693092393262 0.541344968359402 –0.750185830858461 3.33066907387547$ \times 10^{-16} $ 原有方法 0.379693074143900 0.541344942340492 –0.750185794801938 9.61269086552363$ \times 10^{-8} $ 2 MPFR –0.278818336478534 0.915513779528807 0.289991128719866 0 本文方法 –0.278818336478534 0.915513779528807 0.289991128719866 0 原有方法 –0.278818323077561 0.915513735526051 0.289991114781891 9.61269088772809$ \times 10^{-8} $ 3 MPFR –0.831816250860921 –0.330299029958951 0.446076535598833 2.22044604925031$ \times 10^{-16} $ 本文方法 –0.831816250860921 –0.330299029958951 0.446076535598833 2.22044604925031$ \times 10^{-16} $ 原有方法 –0.831816210880958 0.330299014083639 0.446076514158853 9.61269082111471$ \times 10^{-8} $
下载: 导出CSV
表 3 卡塞格林型空间相机参数列表
Table 3. Parameter list for Cassegrain space camera
序号 表面类型 曲率半径 厚度 材料 膜层 圆锥系数 0 物面 标准面 Inf 500000000.000000 ———— 0 0 1 (孔径) 标准面 Inf 4500.000000 ———— 0 0 2 光阑(孔径) 标准面 –10, 478.500000 –3686.000000 MIRROR 0 –1.05000 3 标准面 –3, 846.00000 3689.000000 MIRROR 0 –2.50000 4 标准面 Inf 807.00000 ———— 0 0 5 标准面 Inf 2, 700.000000 ———— 0 0 6 标准面 1560.200000 150.000000 SILICA 0 0 7 标准面 5398.400000 210.000000 ———— 0 0 8 标准面 –2746.700000 110.000000 SILICA 0 0 9 标准面 4516.200000 185.000000 ———— 0 0 10 标准面 –2790.900000 100.000000 SILICA 0 0 11 标准面 1837.600000 150.000000 ———— 0 0 12 标准面 Inf 0.700000 BK7 0 0 13 标准面 Inf 0.750000 ———— 0 0 14 像面 标准面 Inf ———— ———— 0 0
下载: 导出CSV
表 4 卡塞格林型空间相机光线追迹结果
Table 4. Results of ray tracing algorithm for Cassegrain space camera
面序号 算法类别 交点$ P $坐标 残差$ |F(P_x, P_y, P_z)| $ $ P_x $ $ P_y $ $ P_z $ OBJ 本文方法 0 4.00000000000000$ \times 10^{6} $ 0 美国商业软件Zemax 0 4.00000000000000$ \times 10^{6} $ 0 1 本文方法 0 1.53512783172994$ \times 10^{3} $ 0 6.86463863530662$ \times 10^{-9} $ 美国商业软件Zemax 0 1.53512783170000$ \times 10^{3} $ 0 2.30754721997073$ \times 10^{-8} $ 2 本文方法 0 1.49999999999948$ \times 10^{3} $ –1.07335208171627$ \times 10^{2} $ 4.68958205601666$ \times 10^{-13} $ 美国商业软件Zemax 0 1.50000000000000$ \times 10^{3} $ –1.07335208170000$ \times 10^{2} $ 1.70095404428139$ \times 10^{-9} $ 3 本文方法 0 4.16656071439095$ \times 10^{2} $ –2.24707333697088$ \times 10^{1} $ 1.70530256582424$ \times 10^{-13} $ 美国商业软件Zemax 0 4.16656071440000$ \times 10^{2} $ –2.24707333700000$ \times 10^{1} $ 1.93832505601677$ \times 10^{-10} $ 4 本文方法 0 1.25622942628122$ \times 10^{2} $ 0 1.14219744773436$ \times 10^{-9} $ 美国商业软件Zemax 0 1.25622942630000$ \times 10^{2} $ 0 3.02019032005774$ \times 10^{-9} $ 5 本文方法 0 6.23424396084419$ \times 10^{1} $ 0 9.31940746795590$ \times 10^{-10} $ 美国商业软件Zemax 0 6.23424396090000$ \times 10^{1} $ 0 1.49004364402572$ \times 10^{-9} $ 6 本文方法 0 –1.49943013287087$ \times 10^{2} $ 7.22185051869110$ \times 10^{0} $ 2.16459739021957$ \times 10^{-9} $ 美国商业软件Zemax 0 –1.49943013290000$ \times 10^{2} $ 7.22185051870000$ \times 10^{0} $ 8.48085619509220$ \times 10^{-7} $ 7 本文方法 0 –1.53288434563366$ \times 10^{2} $ 2.17676371435573$ \times 10^{0} $ 4.69299266114831$ \times 10^{-10} $ 美国商业软件Zemax 0 –1.53288434560000$ \times 10^{2} $ 2.17676371440000$ \times 10^{0} $ 1.51018321048468$ \times 10^{-6} $ 8 本文方法 0 –1.62777534965079$ \times 10^{2} $ –4.82758062839639$ \times 10^{0} $ 1.53522705659270$ \times 10^{-9} $ 美国商业软件Zemax 0 –1.62777534960000$ \times 10^{2} $ –4.82758062840000$ \times 10^{0} $ 1.67483449331485$ \times 10^{-6} $ 9 本文方法 0 –1.68760549772527$ \times 10^{2} $ 3.15420842636740$ \times 10^{0} $ 1.62981450557709$ \times 10^{-9} $ 美国商业软件Zemax 0 –1.68760549770000$ \times 10^{2} $ 3.15420842640000$ \times 10^{0} $ 1.14553768071346$ \times 10^{-6} $ 10 本文方法 0 –1.84834455036683$ \times 10^{2} $ –6.12729217781634$ \times 10^{0} $ 4.67116478830576$ \times 10^{-9} $ 美国商业软件Zemax 0 –1.84834455040000$ \times 10^{2} $ –6.12729217780000$ \times 10^{0} $ 1.32187415147200$ \times 10^{-6} $ 11 本文方法 0 –1.94567071101658$ \times 10^{2} $ 1.03295178756579$ \times 10^{1} $ 3.26690496876836$ \times 10^{-9} $ 美国商业软件Zemax 0 –1.94567071100000$ \times 10^{2} $ 1.03295178760000$ \times 10^{1} $ 1.89214915735647$ \times 10^{-6} $ 12 本文方法 0 –2.18853927906069$ \times 10^{2} $ 0 5.68434188608080$ \times 10^{-13} $ 美国商业软件Zemax 0 –2.18853927910000$ \times 10^{2} $ 0 3.93043819713057$ \times 10^{-9} $ 13 本文方法 0 –2.18933499087856$ \times 10^{2} $ 0 1.08002495835535$ \times 10^{-12} $ 美国商业软件Zemax 0 –2.18933499090000$ \times 10^{2} $ 0 2.14291162592417$ \times 10^{-9} $ 14 本文方法 0 –2.19063914207259$ \times 10^{2} $ 0 7.95807864051312$ \times 10^{-13} $ 美国商业软件Zemax 0 –2.19063914210000$ \times 10^{2} $ 0 2.74022227131354$ \times 10^{-9} $
下载: 导出CSV
表 5 离轴三反型空间相机光学结构参数列表
Table 5. Parameter list for off-axis three-mirror-anastigmat space camera
序号 表面类型 曲率半径 厚度 材料 膜层 净口径 机械半径 圆锥系数 0 物面-标准面 Inf Inf ———— 0 Inf Inf 0 1 标准面 Inf 633.705045750000 ———— 0 367.133805130855 367.133805130855 0 2 偶次非球面 –2692.02764249986 –633.705045750000 MIRROR 0 271.014896814696 271.014896814696 –2.60071000000000 3 光阑-偶次非球面 –963.158099999982 633.705045750000 MIRROR 0 45.500175946250 45.500175946250 –0.76689900000000 4 偶次非球面 –1476.14695499995 –1132.48912577100 MIRROR 0 251.605408250266 251.605408250266 0.01160100000000 5 像面-标准面 Inf ———————— ———— 0 231.196769640532 231.196769640532 0
下载: 导出CSV
表 6 离轴三反型空间相机单光线追迹与Zemax数值比较
Table 6. Single ray tracing for off-axis three-mirror-anastigmat space camera
面序号 算法类别 交点$ P $坐标 残差$ |F(P_x, P_y, P_z)| $ $ P_x $ $ P_y $ $ P_z $ OBJ 本文方法 0 Inf Inf 0 美国商业软件Zemax 0 Inf Inf 0 1 本文方法 0 –2.01651556349517$ \times 10^{2} $ 0 4.62705429526977$ \times 10^{-11} $ 美国商业软件Zemax 0 –2.01651556350000$ \times 10^{2} $ 0 4.36727987107588$ \times 10^{-10} $ 2 本文方法 0 –1.03337392022989$ \times 10^{2} $ –1.98221886405031$ \times 10^{0} $ 6.78487441703801$ \times 10^{-13} $ 美国商业软件Zemax 0 –1.03337392020000$ \times 10^{2} $ –1.98221886410000$ \times 10^{0} $ 1.63615205928275$ \times 10^{-10} $ 3 本文方法 0 4.55199992296308$ \times 10^{1} $ –1.07580474621568$ \times 10^{0} $ 3.79696274421804$ \times 10^{-14} $ 美国商业软件Zemax 0 4.55199992300000$ \times 10^{1} $ –1.07580474620000$ \times 10^{0} $ 3.30953042748661$ \times 10^{-11} $ 4 本文方法 0 2.52430579518327$ \times 10^{2} $ –2.17467853091218$ \times 10^{1} $ 1.98810369209101$ \times 10^{-13} $ 美国商业软件Zemax 0 2.52430579520000$ \times 10^{2} $ –2.17467853090000$ \times 10^{1} $ 4.12472341438513$ \times 10^{-10} $ 5 本文方法 0 2.32101258958268$ \times 10^{2} $ 0 6.82121026329696$ \times 10^{-13} $ 美国商业软件Zemax 0 2.32101258960000$ \times 10^{2} $ 0 1.73130842995306$ \times 10^{-9} $
下载: 导出CSV
-
[1] 郭疆, 朱磊, 赵继, 龚大鹏 2021 光学精密工程 27 1138
Google Scholar
Guo J, Zhu L, Zhao J, Gong D P 2021 Opt. Precision Eng. 27 1138
Google Scholar
[2] 高洋, 王书新, 齐光, 孙斌, 伞兵, 李景林 2022 光学技术 48 562
Google Scholar
Gao Y, Wang S X, Qi G, Sun B, San B, Li J L 2022 Opt. Techn. 48 562
Google Scholar
[3] 孟庆宇, 汪洪源, 王维, 秦子长, 王晓东 2021 光学精密工程 29 72
Google Scholar
Meng Q Y, Wang H Y, Wang W, Qin Z C, Wang X D 2021 Opt. Precision Eng. 29 72
Google Scholar
[4] Zhong C L, Sang X Z, Yan B B, Li H, Chen D, Qin X J 2022 Opt. Express 30 40087
Google Scholar
[5] [6] Whitted T 1980 Commun. ACM 23 6
[7] Veach E 1997 Ph. D. Dissertation (Stanford: Stanford University)
[8] Braddick H J J 1960 Rep. Prog. Phys. 23 154
Google Scholar
[9] 王之江 1985 光学设计理论基础 (第二版) (北京: 科学出版社) 第3—36 页
Wang Z J 1985 Fundamental Theory of Lens Design (2nd Ed.) (Beijing: Science Press) pp3–36 (in Chinese)
[10] 王涌天 1990 光学技术 5 2
Wang Y T 1990 Opt. Techn. 5 2
[11] 李林, 安连生 2002 计算机辅助光学设计的理论与应用 (北京: 国防工业出版社) 第1—38 页
Li L, An L S 2002 Theory and Application of Computer Aided Optical Design (Beijing: National Defense Industry Press) pp1–38 (in Chinese)
[12] 李晓彤, 岑兆丰 2021 几何光学·像差·光学设计 (第4 版) (杭州: 浙江大学出版社) 第162—179 页
Li X T, Cen Z F 2021 Geometrical Optics, Aberrations and Optical Design (4th Ed.) (Hangzhou: Zhejiang University Press) pp162–179 (in Chinese)
[13] 张以谟, 张红霞, 贾大功 2021 应用光学 (第5版) (北京: 电子工业出版社) 第14—21 页
Zhang Y M, Zhang H X, Jia D G 2021 Applied Optics (5th Ed.) (Beijing: Publishing House of Electronics Industry) pp14–21(in Chinese)
[14] Marrs A, Shirley P, Wald I 2021 Ray Tracing Gems Ⅱ: Next Generation Real-Time Rendering with DXR, Vulkan, and OptiX (1st Ed.) (New York: Apress) pp545–550
[15] 步志超, 张淳民, 赵葆常, 朱化春 2009 58 2415
Google Scholar
Bu Z C, Zhang C M, Zhu H C 2009 Acta Phys. Sin. 58 2415
Google Scholar
[16] Spence S E, Parks A D 2016 Appl. Opt. 55 C46
Google Scholar
[17] 王楠, 阮双琛 2020 69 024201
Google Scholar
Wang N, Ruan S C 2020 Acta Phys. Sin. 69 024201
Google Scholar
[18] Schedin S, Hallberg P, Behndig A 2017 Appl. Opt. 56 9787
Google Scholar
[19] Ferrer-Rodríguez J P, Saura J M, Fernández E F, Almonacid F, Talavera D L, Pérez-Higueras P 2020 Opt. Express 28 6609
Google Scholar
[20] Huang F, Ren H, Shen Y, Wang P F 2021 Appl. Opt. 60 2574
Google Scholar
[21] Sun Q L, Wang C L, Fu Q, Dun X, Heidrich W 2021 ACM Trans. Graph. 40 71
Google Scholar
[22] Halé A, Trouvé-Peloux P, Volatier J B 2021 Opt. Express 29 34748
Google Scholar
[23] Liu A Q, Su L J, Yuan Y, Ding X M 2020 Opt. Express 28 2251
Google Scholar
[24] Marschner S, Shirley P 2022 Fundamentals of Computer Graphics (5th Ed.) (New York: CRC Press) pp80–95
[25] Higham N J 2002 Accuracy and Stability of Numerical Algorithms (2nd Ed.) (Philadelphia: SIAM) pp35–60
[26] Fousse L, Hanrot G, Lefèvre V, Pélissier P, Zimmermann P 2007 ACM Trans. Math. Softw. 33 13
Google Scholar
下载:
计量
- 文章访问数: 5100
- PDF下载量: 161
- 被引次数: 0
