-
为取得理想的隔声性能, 本文结合多孔介质和周期结构两类声振调控方案, 讨论了一种新型含多孔介质周期复合结构; 采用等效模型描述振子系统, 利用薄板理论和Biot理论建立了相应的声振耦合理论模型. 利用此模型计算得出的结果与文献中数据吻合良好. 研究结果表明, 采用简单振子系统或组合振子系统都可以在其特征频率决定的频域提升复合结构的声传递损失 (STL); 然而, 在越过相应频域后, STL会急剧下降, 选取合适的振子参数, 可以拓展隔声带宽而又保持其STL水平. 对比振子系统结果发现, 相对简单振子系统, 组合振子系统能在获得更宽STL提升频域同时减弱特征频率域后的STL下降趋势. 这些结果可以为宽频减振降噪提供思路, 为中低频域隔声应用设计提供理论参考.To obtain excellent sound reduction performance, in this paper we introduce a novel periodic poroelastic composite structure, which combines poroelastic material and periodic structure and aims at using the remarkable acoustic performance of these two. This periodic composite structure comprises three parts, i.e. the poroelastic domain, the elastic domain (thin plate), and the periodic resonators, which can be simple single-degree-of-freedom resonators (SRs) or composite two-degree-of-freedom resonators (CRs). A theoretical model is established by using Biot theory for the poroelastic domain, and by using the effective medium method for the resonator-plate coupling system, which is considered as an isotropic plate with an equivalent dynamic density. This method is validated with degenerated model in the literature; the results obtained by this method are in excellent consistence with the results in the literature. Parameter analyses are performed to test the influences of poroelastic addition and periodic resonator on the sound transmission loss (STL) of this periodic composite structure under two kinds of boundary conditions. The poroelastic addition is found to increase the STL while the influences of resonators are complicated. The STL increases notably in the frequency range bounded by the characteristic frequencies of these resonators, however, a decrease just follows when it exceeds these frequencies, which can be observed in both SR case and CR case under the two boundary conditions. In the meantime, when multiple SR is placed in a periodic lattice, it is found that different resonators with ascending mass and characteristic frequencies have superior STL to those with ascending characteristic frequencies but have equal mass. The case with CR, which is more complicated as expected, shows less STL decrease than the case with SR, but wider frequency range where the STL increases than a poroelastic composite structure without resonators. This results from the fact that the frequency band of vibration suppression in the CR case is wider than in the SR case. As a result, to achieve the desired STL performance in a frequency range, the proposed composite structure using SR with tuned characteristic frequencies is enough; however, if a wider frequency band is expected even if there is a slight STL tradeoff, the CR case is a better option. Though the method proposed is only valid in the low-to-medium frequency range, the results obtained can benefit theoretical development of low-to-medium sound modulation applications, they are also valuable and illuminating for investigating the broadband sound modulation.
-
Keywords:
- poroelastic materials /
- periodic structures /
- sound transmission
[1] Allard J F, Atalla N 2009 Propagation of Sound in Porous Media (Chichester: John Wiley & Sons) pp111−134
[2] Deckers E, Jonckheere S, Vandepitte D, Desmet W 2015 Arch. Comput. Methods Eng. 22 183
Google Scholar
[3] Bolton J S, Shiau N M, Kang Y J 1996 J. Sound Vib. 191 317
Google Scholar
[4] Zhou J, Bhaskar A, Zhang X 2013 J. Sound Vib. 332 3724
Google Scholar
[5] Liu Y 2015 J. Sound Vib. 339 376
Google Scholar
[6] Qiao H, He Z, Jiang W, Peng W 2019 J. Sound Vib. 440 256
Google Scholar
[7] Allard J F, Depollier C, Rebillard P, Lauriks W, Cops A 1989 J. Appl. Phys. 66 2278
Google Scholar
[8] Deresiewicz H 1961 Bull. Seismol. Soc. Am. 51 51
[9] Zhou J, Bhaskar A, Zhang X 2013 Appl. Acoust. 74 1422
Google Scholar
[10] Liu Y, Sebastian A 2015 J. Sound Vib. 344 399
Google Scholar
[11] Talebitooti R, Daneshjou K, Kornokar M 2016 J. Sound Vib. 363 380
Google Scholar
[12] Shojaeifard M H, Talebitooti R, Ranjbar B, Ahmadi R 2014 Appl. Math. Mech. 35 1447
Google Scholar
[13] Schanz M 2009 Appl. Mech. Rev. 62 030803
Google Scholar
[14] Panneton R, Atalla N 1997 J. Acoust. Soc. Am. 101 3287
Google Scholar
[15] Verdière K, Panneton R, Elkoun S, Dupont T, Leclaire P 2013 J. Acoust. Soc. Am. 134 4648
Google Scholar
[16] Brillouin L 2003 Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices (New York: Dover Publications) pp1−16
[17] Mead D M 1996 J. Sound Vib. 190 495
Google Scholar
[18] 曹永军, 周培勤, 董纯红 2006 55 6470
Google Scholar
Cao Y J, Zhou P Q, Dong C H 2006 Acta Phys. Sin. 55 6470
Google Scholar
[19] 丁昌林, 董仪宝, 赵晓鹏 2018 67 194301
Google Scholar
Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301
Google Scholar
[20] 温熙森 2006 光子/声子晶体理论与技术 (北京: 科学出版社) 第38−341页
Wen X S 2006 Photonic/Phononic Theory and Technology (Beijing: Science Press) pp38−104 (in Chinese)
[21] 姜久龙, 姚宏, 杜军, 赵静波, 邓涛 2017 66 064301
Google Scholar
Jiang J L, Yao H, Du J, Zhao J B, Deng T 2017 Acta Phys. Sin. 66 064301
Google Scholar
[22] 林国昌, 孙宏伟, 谭惠丰, 杜星文 2011 60 034302
Google Scholar
Lin G C, Sun H W, Tan H F, Du X W 2011 Acta Phys. Sin. 60 034302
Google Scholar
[23] 丁昌林, 赵晓鹏 2009 58 6351
Google Scholar
Ding C L, Zhao X P 2009 Acta Phys. Sin. 58 6351
Google Scholar
[24] Yu D L, Shen H J, Liu J W, Yin J F, Zhang Z F, Wen J H 2018 Chin. Phys. B 27 064301
Google Scholar
[25] 张丰辉, 唐宇帆, 辛锋先, 卢天健 2018 67 234302
Zhang F H, Tang Y F, Xin F X, Lu T J 2018 Acta Phys. Sin. 67 234302
[26] 朱席席, 肖勇, 温激鸿, 郁殿龙 2016 65 176202
Google Scholar
Zhu X X, Xiao Y, Wen J H, Yu D L 2016 Acta Phys. Sin. 65 176202
Google Scholar
[27] Chen X, Cai L, Wen J H 2018 Chin. Phys. B 27 057803
Google Scholar
[28] 宋玉宝, 温激鸿, 郁殿龙, 沈惠杰 2018 机械工程学报 54 60
Song Y B, Wen J H, Yu D L, Shen H J 2018 Chin. J. Mech. Eng. 54 60
[29] Kidner M R F, Fuller C R, Gardner B 2006 J. Sound Vib. 294 466
Google Scholar
[30] Idrisi K, Johnson M E, Toso A, Carneal J P 2009 J. Sound Vib. 323 51
Google Scholar
[31] Cui S, Harne R L 2017 J. Acoust. Soc. Am. 141 4715
Google Scholar
[32] Harne R L, Song Y, Dai Q 2017 Extrem. Mech. Lett. 12 41
Google Scholar
[33] Bishop J, Harne R L 2018 Appl. Acoust. 130 222
Google Scholar
[34] 温激鸿, 郁殿龙, 赵宏刚, 蔡力, 肖勇, 王刚, 尹剑飞 2015 人工周期结构中弹性波的传播: 振动与声学特性 (北京: 科学出版社) 第272−290页
Wen J H, Yu D L, Zhao H G, Cai L, Xiao Y, Wang G, Yin J F 2016 Propagation of Elastic Waves in Artificial Periodic Structures: Vibrational and Acoustical Properties (Beijing: Science Press) pp272−290 (in Chinese)
[35] Xiao Y, Wen J, Wen X 2012 J. Sound Vib. 331 5408
Google Scholar
[36] Li P, Yao S, Zhou X, Huang G, Hu G 2014 J. Acoust. Soc. Am. 135 1844
Google Scholar
[37] Xiao Y, Wen J, Wen X 2012 J. Phys. D: Appl. Phys. 45 195401
Google Scholar
[38] Biot M A 1956 J. Acoust. Soc. Am. 28 179
Google Scholar
[39] Junger M C, Feit D 1986 Sound, Structures, and Their Interaction (Massachusetts: MIT Press) pp235−277
[40] 程建春 2012 声学原理 (北京: 科学出版社) 第51页
Cheng J C 2012 Theory of Sound (Beijing: Science Press) p51 (in Chinese)
[41] Den Hartog J P 1985 Mechanical Vibrations (New York: Dover Publications) pp79−121
[42] 何琳, 朱海潮, 邱小军, 杜功焕 2006 声学理论与工程应用 (北京: 科学出版社) 第173−184页
He L, Zhu H C, Qiu X J, Du G H 2006 Theory and Engineering Applications of Acoustics (Beijing: Science Press) pp173−184 (in Chinese)
[43] Peng H, Frank Pai P, Deng H 2015 Int. J. Mech. Sci. 103 104
Google Scholar
-
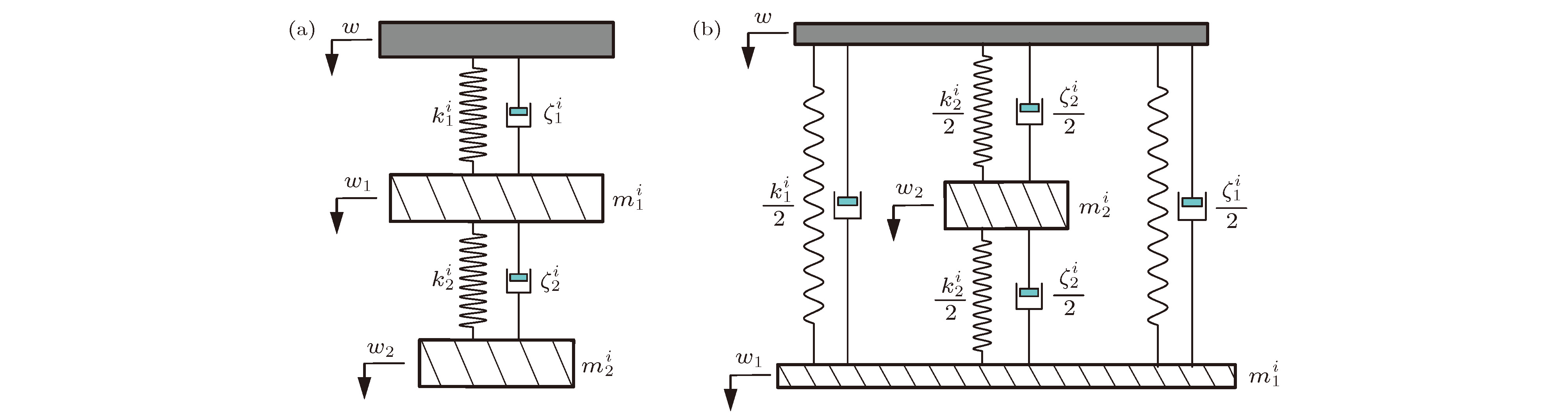
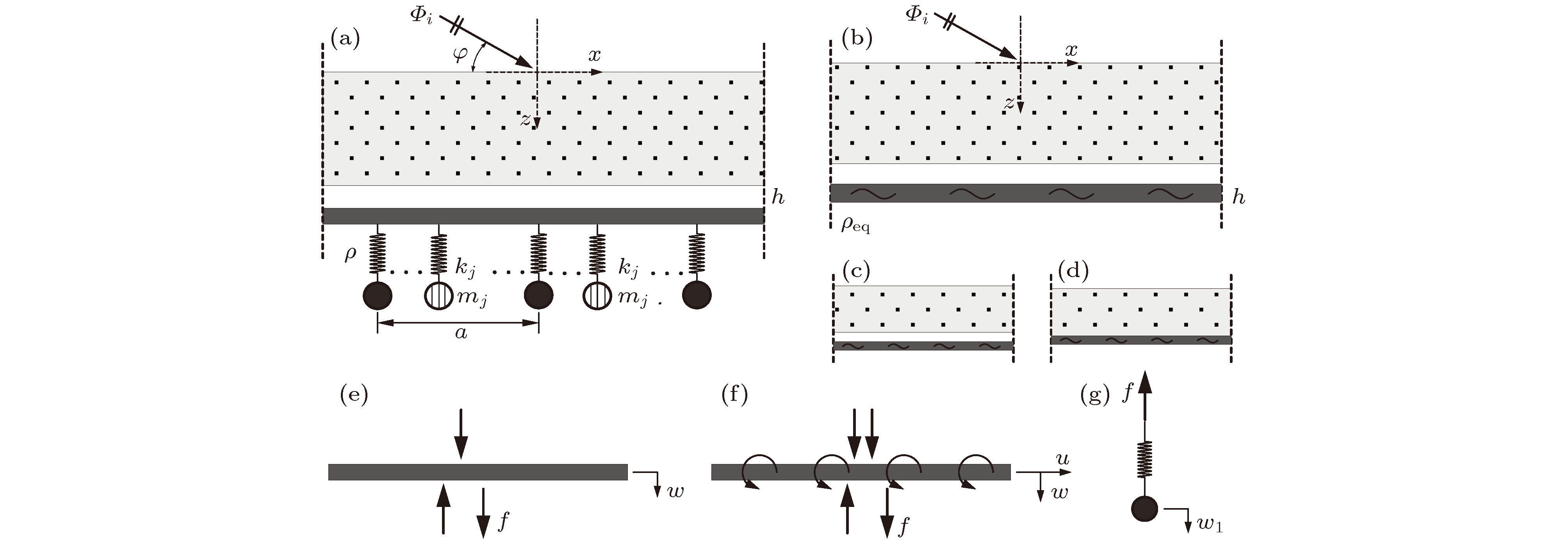
图 1 含多孔介质复合结构及其子结构示意图 (a) 含多孔介质复合结构; (b) 等效模型; (c) OU边界; (d) OB边界; (e) 板受力情况(OU边界); (f) 板受力情况(OB边界); (g) 弹簧振子受力
Fig. 1. Schematic of the poroelastic composite structure and its substructures: (a) The poroelastic composite structure; (b) the equivalent model; (c) the OU boundary connection; (d) the OB boundary connection; (e) the forces in OU boundary case; (f) the forces in OB boundary case; (g) the forces in a simple spring-mass resonator.
图 2 组合振子系统示意图 (a) 串联弹簧振子系统A; (b) 复合弹簧振子系统B
Fig. 2. Schematic of the composite-resonator-structure: (a) Composite resonator type A, two resonators placed in serial connection; (b) composite resonator type B, two resonators placed in composite connection.
图 3 周期振子排布方式示意图 (a) 简单振子周期分布, 按各个振子质量
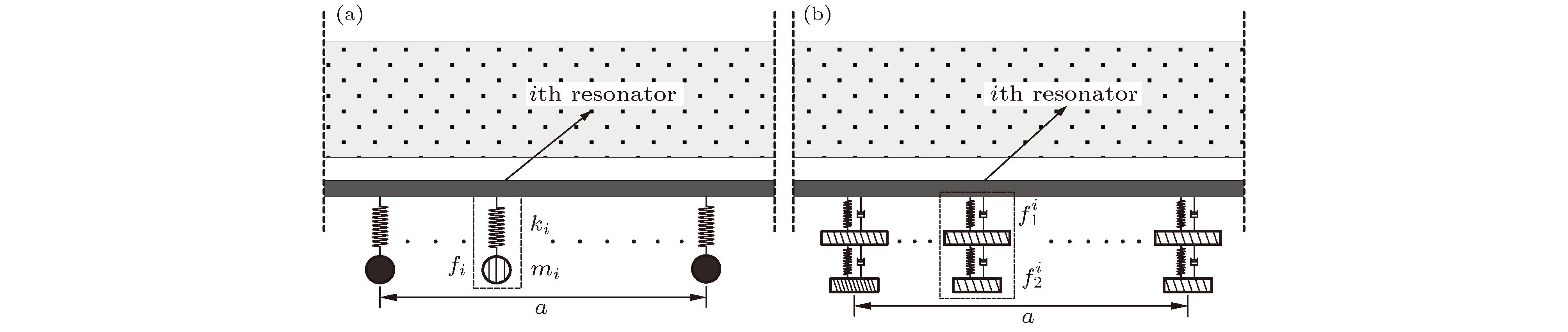
${m_i}$ 和特征频率${f_i}$ 分为多个振子情况 (N1SR,${m_i}$ 和${f_i}$ 均保持恒定) 和多种振子情况 (NNSR,${m_i}$ 或${f_i}$ 不相同); (b) 组合振子周期分布, 按振子部件质量$m_n^i$ 和特征频率$f_n^i$ 分为多个振子情况 (N1CR,$m_n^i$ 和$f_n^i$ 均保持恒定) 和多种振子情况 (NNCR,$m_n^i$ 或$f_n^i$ 不相同); 图中虚线框内部分为单个振子单元, (b)中虚线框部分可替换为 图2中B类组合振子Fig. 3. Schematic of the arrangement of periodic resonators: (a) An array of simple resonators, denoted as multiple resonators (N1SR, with constant
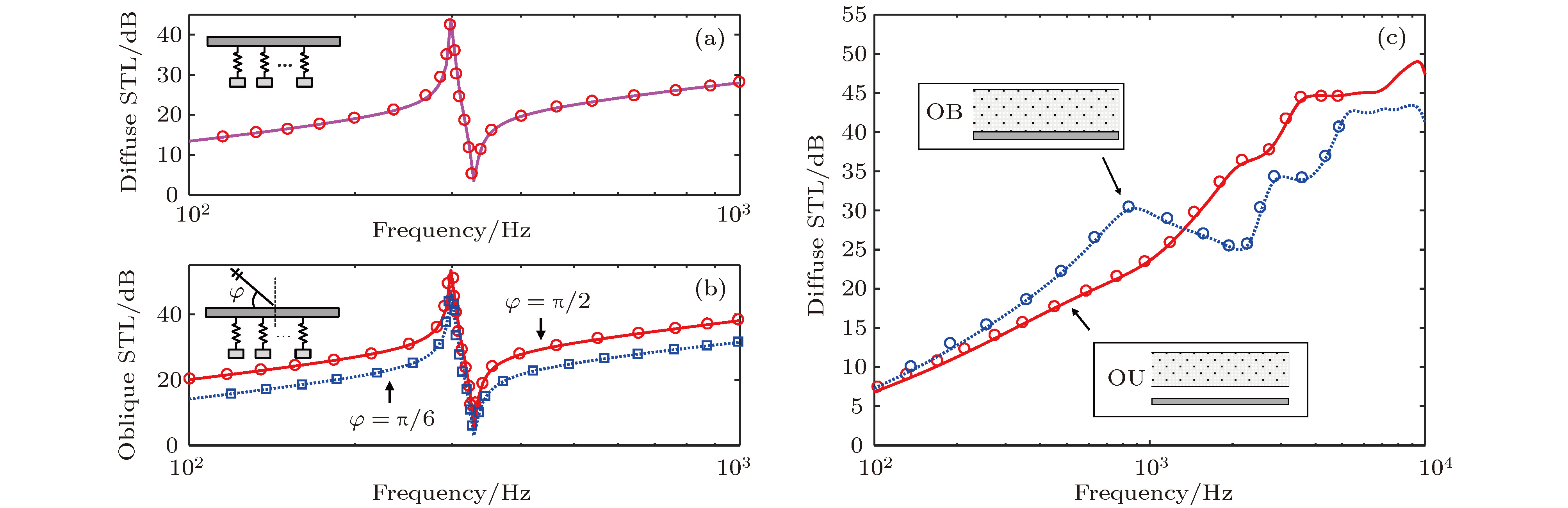
${m_i}$ and${f_i}$ ) or multiple kinds of resonators (NNSR, with different${m_i}$ and${f_i}$ ); (b) an array of composite resonators, denoted as multiple resonators (N1CR, with constant$m_n^i$ and$f_n^i$ ) or multiple kinds of resonators (NNCR, with different$m_n^i$ or$f_n^i$ ). The area in the dash-line denotes the periodic lattice, in panel (b), the composite resonator can be type B in Fig. 2
图 4 不同类型隔声结构验证算例 (a) 文献[35]随机入射情况; (b) 文献[35]斜入射情况; (c) 文献[3]含多孔介质复合结构; 其中, 各曲线为本文结果, 各标记为文献中结果
Fig. 4. Validation of the results here with previous results: (a) The diffuse case in Ref. [35]; (b) the oblique incident cases in Ref. [35]; (c) the composite poroelastic structure without resonator in Ref. [3]. The lines are results obtained here, while the marks are the results in the references.
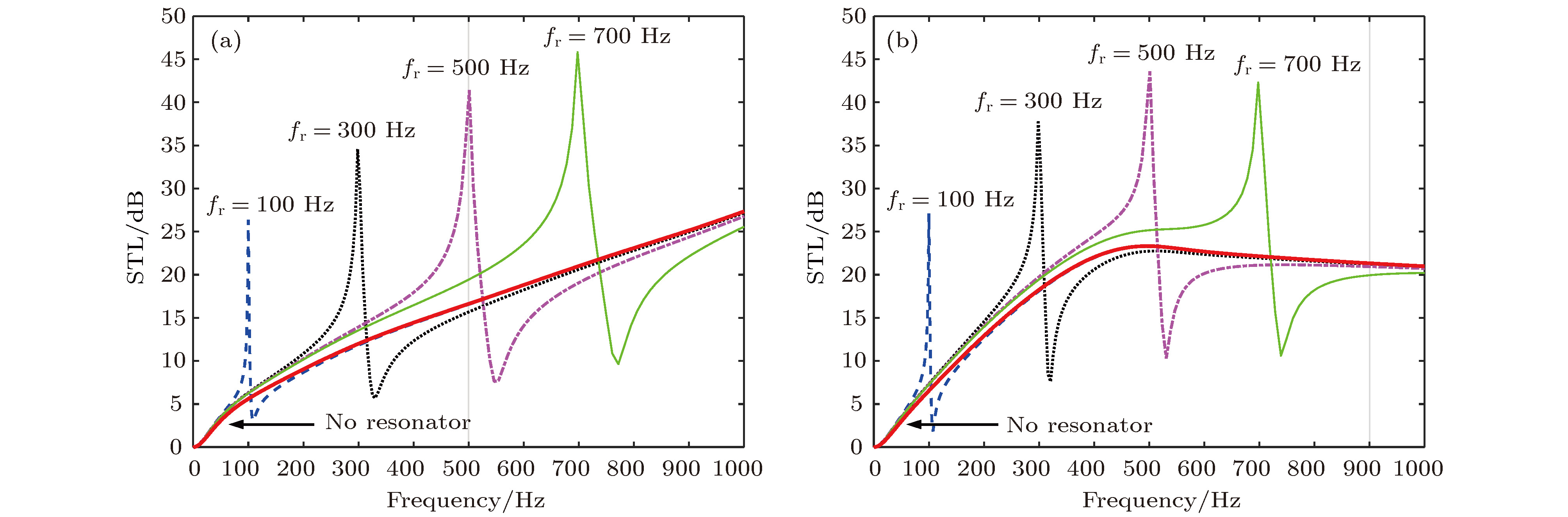
图 5 有无多孔材料对含不同特征频率振子系统复合结构STL的影响 (a) OU边界情况; (b) OB边界情况; 有无多孔介质分别与相应实线和虚线对应
Fig. 5. Influence of porous material on the STL of the multiple-single-type-resonator composite structure with different characteristic frequencies: (a) OU case; (b) OB case. The solid lines correspond to cases with porous materials.
图 6 含相同简单振子系统复合结构(fr = 300 Hz)有无多孔介质及相应不含振子复合结构的STL (有多孔介质, Porous + Resonator; 无多孔介质, Resonator; 相应不含振子复合结构, Porous) (a) OU边界情况; (b) OB边界情况.
Fig. 6. The STL of multiple-single-type-resonator composite structure (fr = 300 Hz) with/without porous, and composite structure without resonators: (a) OU case; (b) OB case. Composite structure here with porous material: Porous + Resonator. Without porous material: Resonator. Composite structure without resonators: Porous.
图 7 采用不同特征频率简单振子系统对复合结构STL的影响 (a) OU边界; (b) OB边界
Fig. 7. Influences of resonators with different characteristic frequencies on the STL: (a) OU case; (b) OB case.
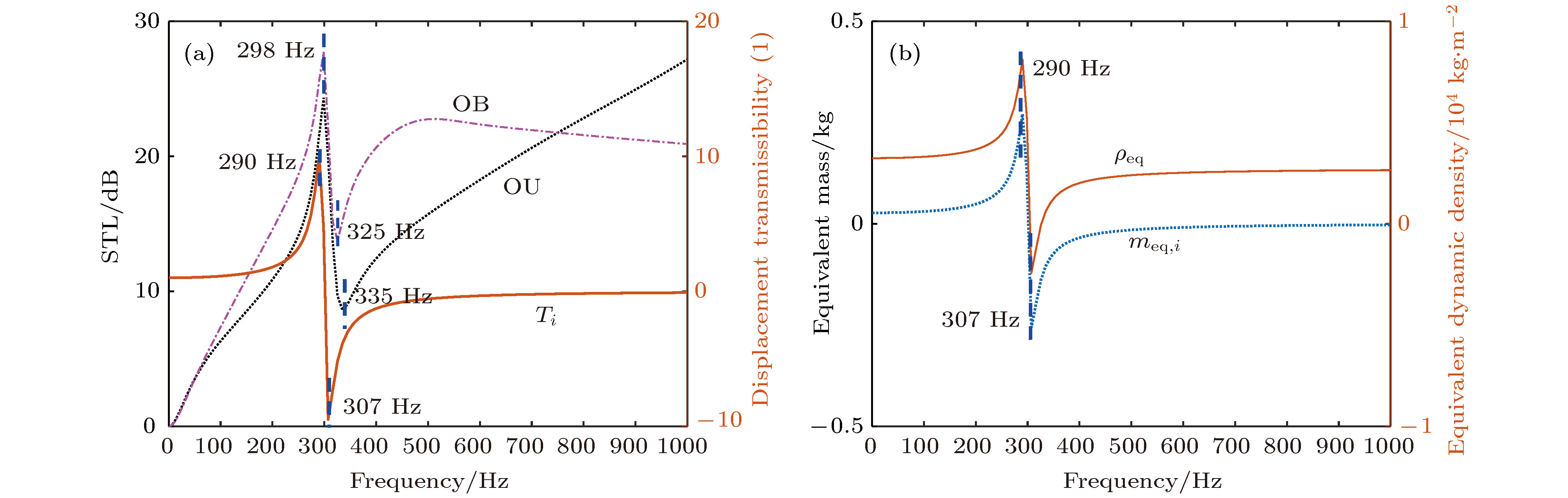
图 8 单一类型简单振子周期排布时 (a) OU, OB情况下STL及其位移传递率Ti; (b) 振子的等效质量meq和板等效动态密度
${\rho _{{\rm{eq}}}}$ Fig. 8. (a) STL of OU and OB case in periodically-arranged single simple resonator case, and its displacement transmissibility Ti; (b) equivalent mass meq of a single resonator and the dynamic density
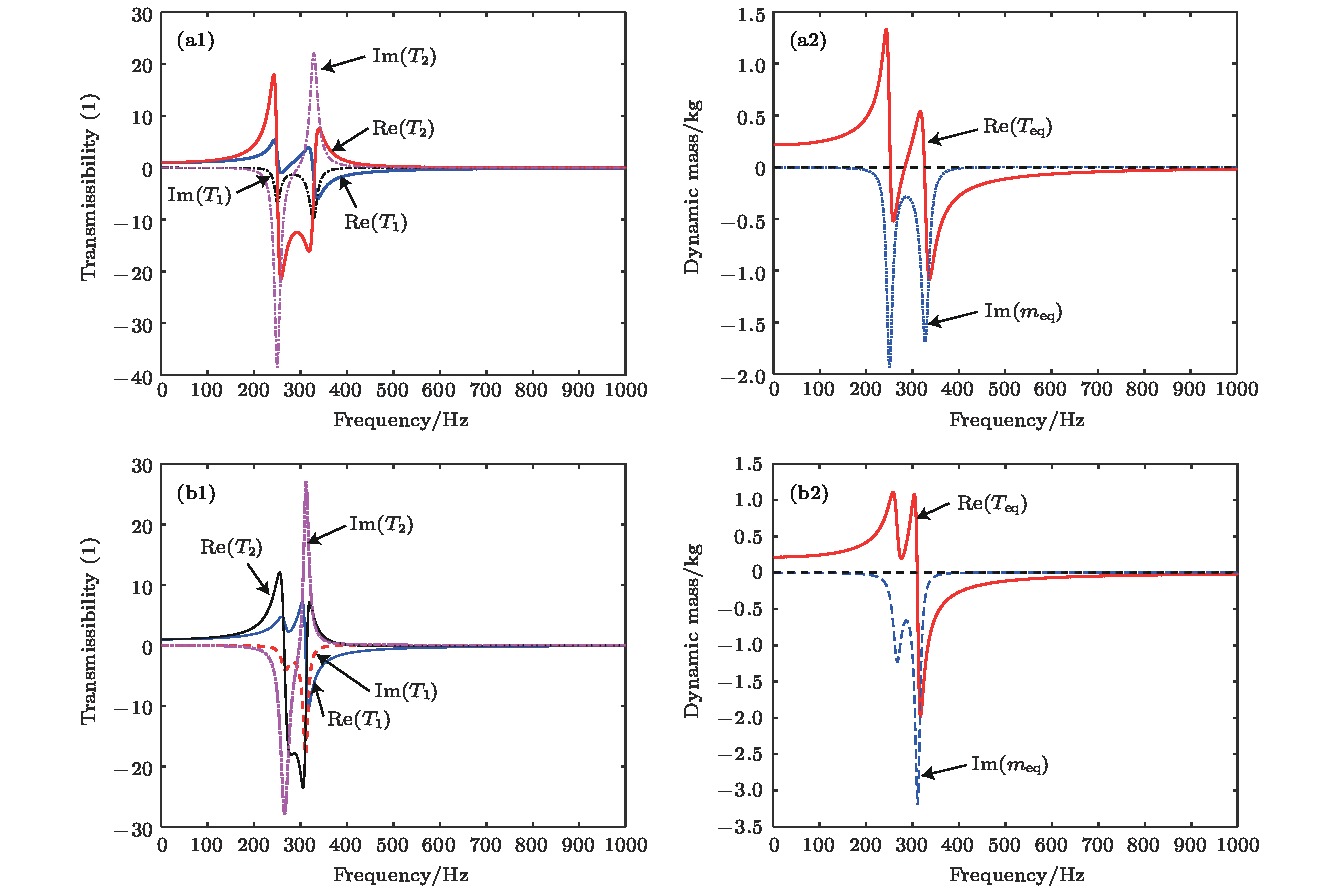
${\rho _{{\rm{eq}}}}$ of the equivalent plate.
图 9 两类组合振子系统中质量块的位移传递率
${T_1}$ ,${T_2}$ 和动态质量${m_{{\rm{eq}}}}$ (a1) 组合振子系统A中各质量块的位移传递率${T_1}$ ,${T_2}$ ; (a2) 组合振子系统A的动态质量${m_{{\rm{eq}}}}$ ; (b1) 组合振子系统B中各质量块的位移传递率${T_1}$ ,${T_2}$ ; (b2) 组合振子系统B的动态质量${m_{{\rm{eq}}}}$ Fig. 9. Displacement transmissibility and dynamic mass of the mass components in the two composite resonators: (a1) Displacement transmissibility
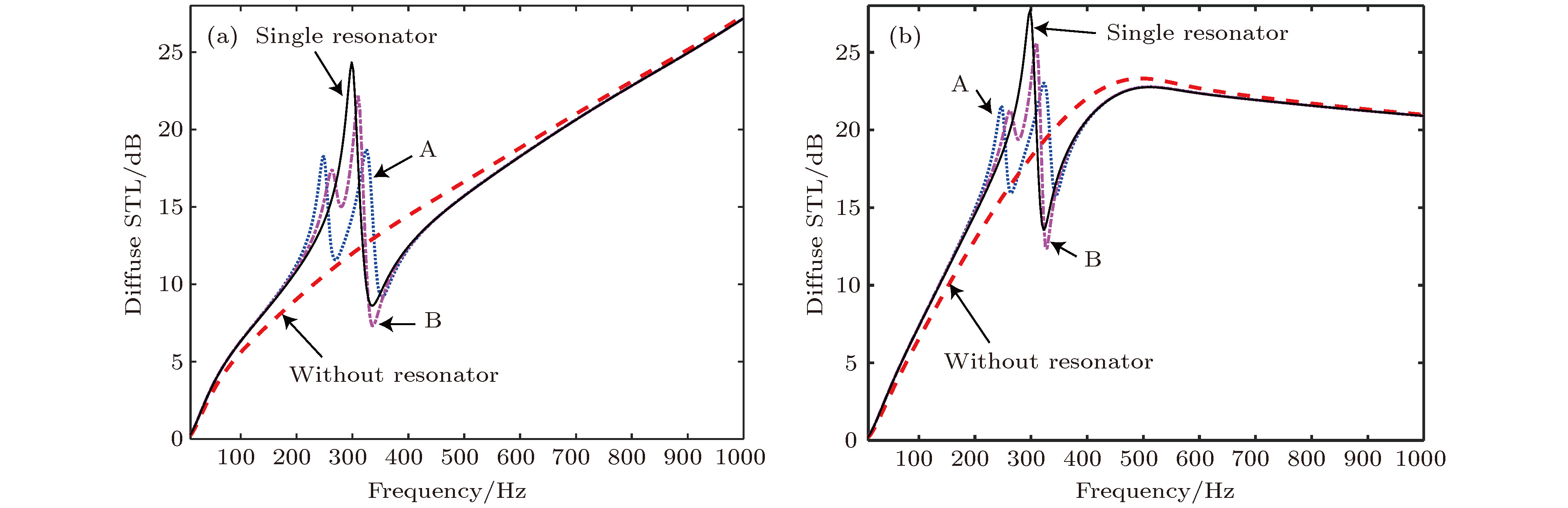
${T_1}$ ,${T_2}$ of composite resonator type A; (a2) dynamic mass${m_{{\rm{eq}}}}$ of composite resonator type A; (b1) displacement transmissibility${T_1}$ ,${T_2}$ of composite resonator type B; (b2) dynamic mass${m_{{\rm{eq}}}}$ of composite resonator type B.
图 10 复合结构周期间隔内分布4个相同简单振子(Single resonator), 组合振子A或组合振子B时的STL和不含振子复合结构(Without resonator)的STL (a) OU边界情况; (b) OB边界情况
Fig. 10. STL of the proposed composite structure with 4 identical simple resonators (Single resonator), composite resonators of type A or B versus its STL without any resonators (Without resonator) in a periodic lattice: (a) OU boundary case; (b) OB boundary case.
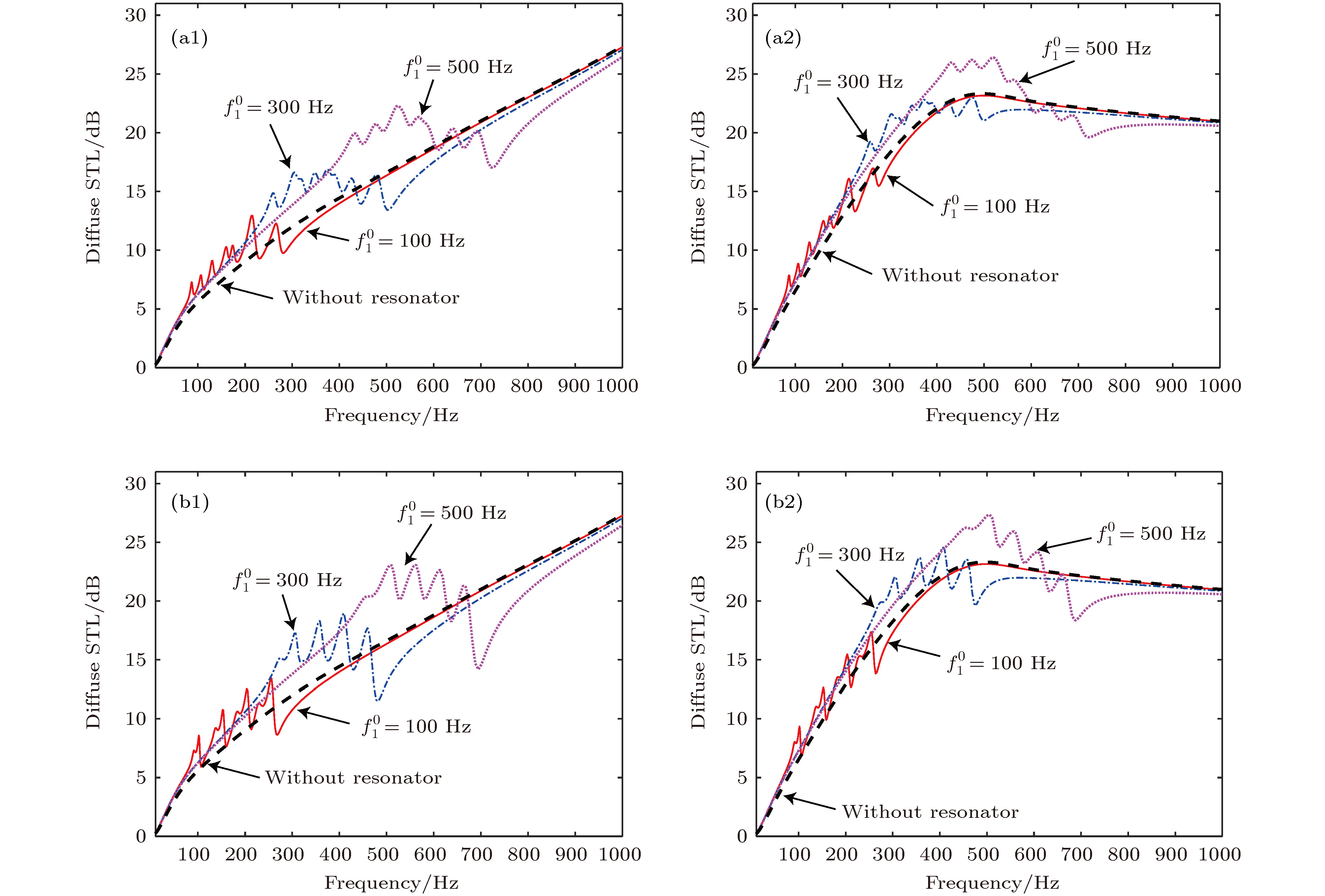
图 11 NNSR分布时OU, OB边界情况下的STL (a1), (a2) 情况A; (b1), (b2) 情况B,
${{\Delta m} / {{m_{{\rm{sum}}}}}} = 0.04$ ; 其中, (a1)和(b1)为OU边界情况, (a2)和(b2)为OB边界情况Fig. 11. STL of the composite structure with NNSR configuration under two boundary cases: (a1), (a2) Case A; (b1), (b2) case B,
${{\Delta m} / {{m_{{\rm{sum}}}}}} = 0.04$ . Here (a1) and (b1) correspond to OU case, (a2) and (b2) correspond to OB case.
图 12 采用组合振子复合结构的STL (a1), (a2) 采用组合振子A; (b1), (b2) 采用组合振子B; 其中, (a1)和(b1)对应于OU边界情况, (a2)和(b2)对应于OB边界情况
Fig. 12. STL of the proposed composite structure under NNCR configuration: (a1), (a2) Composite resonator type A; (b1), (b2) composite resonator type B. Here (a1) and (b1) correspond to OU case, (a2) and (b2) correspond to OB case.
图 13 不同振子系统分布时STL对比 (a), (a1) OU边界情况; (b), (b1) OB边界情况;
$\Delta m = 0$ 和$\Delta m > 0$ 对应简单振子情况NNSR; Type A和Type B对应组合振子情况NNCRFig. 13. STL of different resonator system configuration: (a), (a1) OU case; (b), (b1) OB case.
$\Delta m = 0$ and$\Delta m > 0$ correspond to simple resonator case NNSR. Type A and Type B correspond to composite resonator case NNCR.表 1 振子系统分布情况简称及其对应含义
Table 1. Abbreviations of the distribution of resonator systems and their meanings.
振子系统分布 含义 N1SR 周期间隔内分布多个简单振子系统, 各振子系统${m_i}$和${f_i}$均相等 NNSR 周期间隔内分布多种简单振子系统, 各振子系统${m_i}$或${f_i}$不同 N1CR 周期间隔内分布多个组合振子系统, 各振子系统$m_n^i$和$f_n^i$均相等 NNCR 周期间隔内分布多种组合振子系统, 各振子系统$m_n^i$或$f_n^i$不同 
下载: 导出CSV
表 2 薄板、空气域及振子参数
Table 2. Parameters of plate and resonators.
薄板 空气域(20 ℃, 1 atm) 简单振子 h/mm E/GPa ν ${\rho _{\rm{p}}}$/kg·m–3 ρ/kg·m–3 c0/m·s–1 ha/mm fr/Hz γ 1 70 0.33 2700 1.204 343.21 2 300 0.2
下载: 导出CSV
表 3 多孔材料参数
Table 3. Parameters of the porous media used here
参数 值 参数 值 ${\rho _{\rm{s}}}$/kg·m–3 30 $\epsilon$ 0.9 ${\rho _{\rm{f}}}$/kg·m–3 1.204 ${\tau _\infty }$ 7.8 ${E_{\rm{s}}}$/MPa 0.8(1+0.265${\rm{j}}$) ${\sigma _0}$/MKS rayls 25000 ${\nu _s}$ 0.4 hp/mm 50
下载: 导出CSV
表 4 振子系统参数
Table 4. Parameters of the composite resonators.
参数 $\omega _1^i$ $\omega _2^i$ r s $\eta _1^i$ $\eta _2^i$ 值 600${\text{π}}$ 1088 0.075 0.0625 0.01 0.05
下载: 导出CSV
表 5 组合振子系统参数
Table 5. Parameters of the composite resonators.
参数 r s $\eta _1^i$ $\eta _2^i$ 值 0.045 0.040 0.01 0.05
下载: 导出CSV
-
[1] Allard J F, Atalla N 2009 Propagation of Sound in Porous Media (Chichester: John Wiley & Sons) pp111−134
[2] Deckers E, Jonckheere S, Vandepitte D, Desmet W 2015 Arch. Comput. Methods Eng. 22 183
Google Scholar
[3] Bolton J S, Shiau N M, Kang Y J 1996 J. Sound Vib. 191 317
Google Scholar
[4] Zhou J, Bhaskar A, Zhang X 2013 J. Sound Vib. 332 3724
Google Scholar
[5] Liu Y 2015 J. Sound Vib. 339 376
Google Scholar
[6] Qiao H, He Z, Jiang W, Peng W 2019 J. Sound Vib. 440 256
Google Scholar
[7] Allard J F, Depollier C, Rebillard P, Lauriks W, Cops A 1989 J. Appl. Phys. 66 2278
Google Scholar
[8] Deresiewicz H 1961 Bull. Seismol. Soc. Am. 51 51
[9] Zhou J, Bhaskar A, Zhang X 2013 Appl. Acoust. 74 1422
Google Scholar
[10] Liu Y, Sebastian A 2015 J. Sound Vib. 344 399
Google Scholar
[11] Talebitooti R, Daneshjou K, Kornokar M 2016 J. Sound Vib. 363 380
Google Scholar
[12] Shojaeifard M H, Talebitooti R, Ranjbar B, Ahmadi R 2014 Appl. Math. Mech. 35 1447
Google Scholar
[13] Schanz M 2009 Appl. Mech. Rev. 62 030803
Google Scholar
[14] Panneton R, Atalla N 1997 J. Acoust. Soc. Am. 101 3287
Google Scholar
[15] Verdière K, Panneton R, Elkoun S, Dupont T, Leclaire P 2013 J. Acoust. Soc. Am. 134 4648
Google Scholar
[16] Brillouin L 2003 Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices (New York: Dover Publications) pp1−16
[17] Mead D M 1996 J. Sound Vib. 190 495
Google Scholar
[18] 曹永军, 周培勤, 董纯红 2006 55 6470
Google Scholar
Cao Y J, Zhou P Q, Dong C H 2006 Acta Phys. Sin. 55 6470
Google Scholar
[19] 丁昌林, 董仪宝, 赵晓鹏 2018 67 194301
Google Scholar
Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301
Google Scholar
[20] 温熙森 2006 光子/声子晶体理论与技术 (北京: 科学出版社) 第38−341页
Wen X S 2006 Photonic/Phononic Theory and Technology (Beijing: Science Press) pp38−104 (in Chinese)
[21] 姜久龙, 姚宏, 杜军, 赵静波, 邓涛 2017 66 064301
Google Scholar
Jiang J L, Yao H, Du J, Zhao J B, Deng T 2017 Acta Phys. Sin. 66 064301
Google Scholar
[22] 林国昌, 孙宏伟, 谭惠丰, 杜星文 2011 60 034302
Google Scholar
Lin G C, Sun H W, Tan H F, Du X W 2011 Acta Phys. Sin. 60 034302
Google Scholar
[23] 丁昌林, 赵晓鹏 2009 58 6351
Google Scholar
Ding C L, Zhao X P 2009 Acta Phys. Sin. 58 6351
Google Scholar
[24] Yu D L, Shen H J, Liu J W, Yin J F, Zhang Z F, Wen J H 2018 Chin. Phys. B 27 064301
Google Scholar
[25] 张丰辉, 唐宇帆, 辛锋先, 卢天健 2018 67 234302
Zhang F H, Tang Y F, Xin F X, Lu T J 2018 Acta Phys. Sin. 67 234302
[26] 朱席席, 肖勇, 温激鸿, 郁殿龙 2016 65 176202
Google Scholar
Zhu X X, Xiao Y, Wen J H, Yu D L 2016 Acta Phys. Sin. 65 176202
Google Scholar
[27] Chen X, Cai L, Wen J H 2018 Chin. Phys. B 27 057803
Google Scholar
[28] 宋玉宝, 温激鸿, 郁殿龙, 沈惠杰 2018 机械工程学报 54 60
Song Y B, Wen J H, Yu D L, Shen H J 2018 Chin. J. Mech. Eng. 54 60
[29] Kidner M R F, Fuller C R, Gardner B 2006 J. Sound Vib. 294 466
Google Scholar
[30] Idrisi K, Johnson M E, Toso A, Carneal J P 2009 J. Sound Vib. 323 51
Google Scholar
[31] Cui S, Harne R L 2017 J. Acoust. Soc. Am. 141 4715
Google Scholar
[32] Harne R L, Song Y, Dai Q 2017 Extrem. Mech. Lett. 12 41
Google Scholar
[33] Bishop J, Harne R L 2018 Appl. Acoust. 130 222
Google Scholar
[34] 温激鸿, 郁殿龙, 赵宏刚, 蔡力, 肖勇, 王刚, 尹剑飞 2015 人工周期结构中弹性波的传播: 振动与声学特性 (北京: 科学出版社) 第272−290页
Wen J H, Yu D L, Zhao H G, Cai L, Xiao Y, Wang G, Yin J F 2016 Propagation of Elastic Waves in Artificial Periodic Structures: Vibrational and Acoustical Properties (Beijing: Science Press) pp272−290 (in Chinese)
[35] Xiao Y, Wen J, Wen X 2012 J. Sound Vib. 331 5408
Google Scholar
[36] Li P, Yao S, Zhou X, Huang G, Hu G 2014 J. Acoust. Soc. Am. 135 1844
Google Scholar
[37] Xiao Y, Wen J, Wen X 2012 J. Phys. D: Appl. Phys. 45 195401
Google Scholar
[38] Biot M A 1956 J. Acoust. Soc. Am. 28 179
Google Scholar
[39] Junger M C, Feit D 1986 Sound, Structures, and Their Interaction (Massachusetts: MIT Press) pp235−277
[40] 程建春 2012 声学原理 (北京: 科学出版社) 第51页
Cheng J C 2012 Theory of Sound (Beijing: Science Press) p51 (in Chinese)
[41] Den Hartog J P 1985 Mechanical Vibrations (New York: Dover Publications) pp79−121
[42] 何琳, 朱海潮, 邱小军, 杜功焕 2006 声学理论与工程应用 (北京: 科学出版社) 第173−184页
He L, Zhu H C, Qiu X J, Du G H 2006 Theory and Engineering Applications of Acoustics (Beijing: Science Press) pp173−184 (in Chinese)
[43] Peng H, Frank Pai P, Deng H 2015 Int. J. Mech. Sci. 103 104
Google Scholar
下载:
计量
- 文章访问数: 7799
- PDF下载量: 73
- 被引次数: 0
