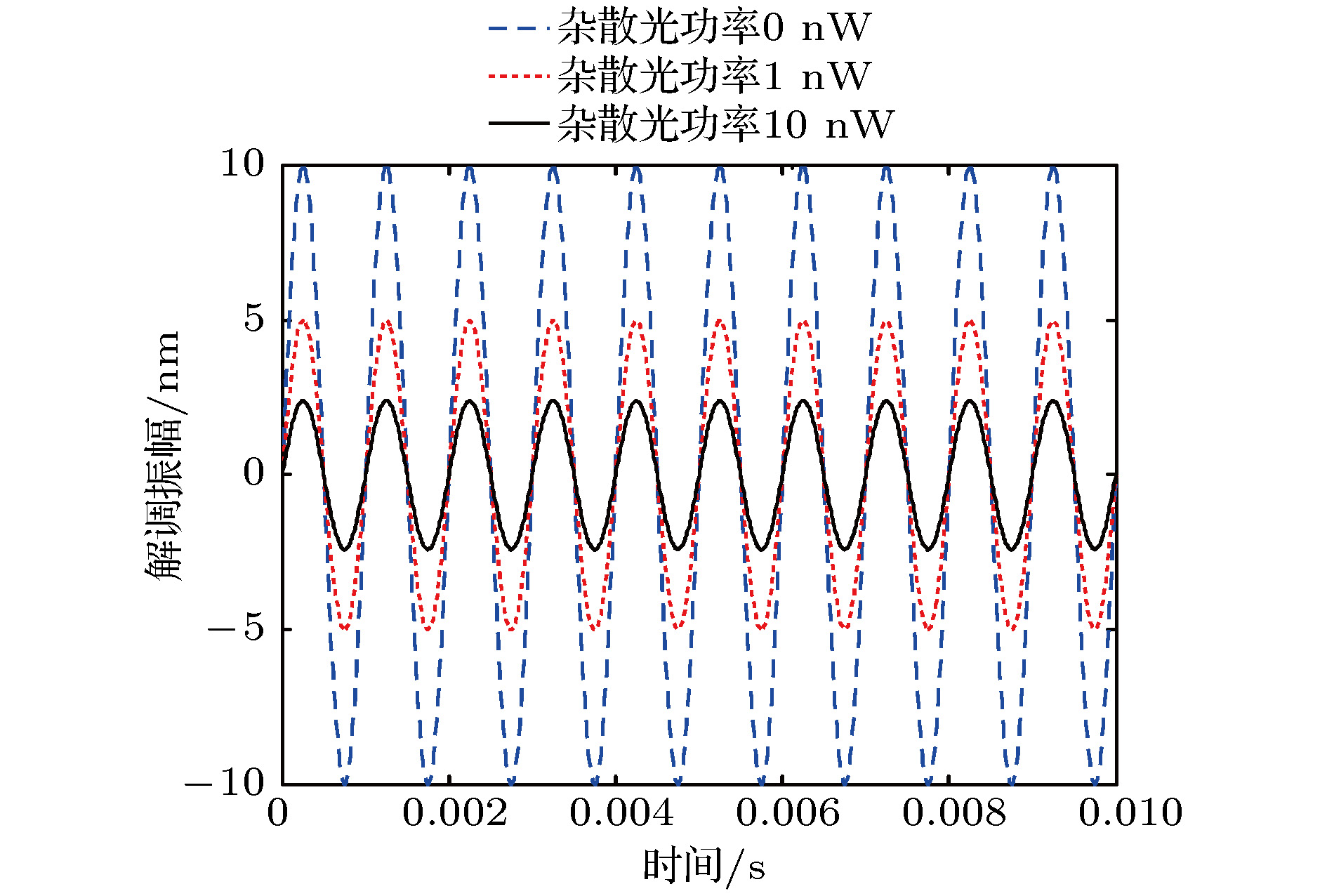
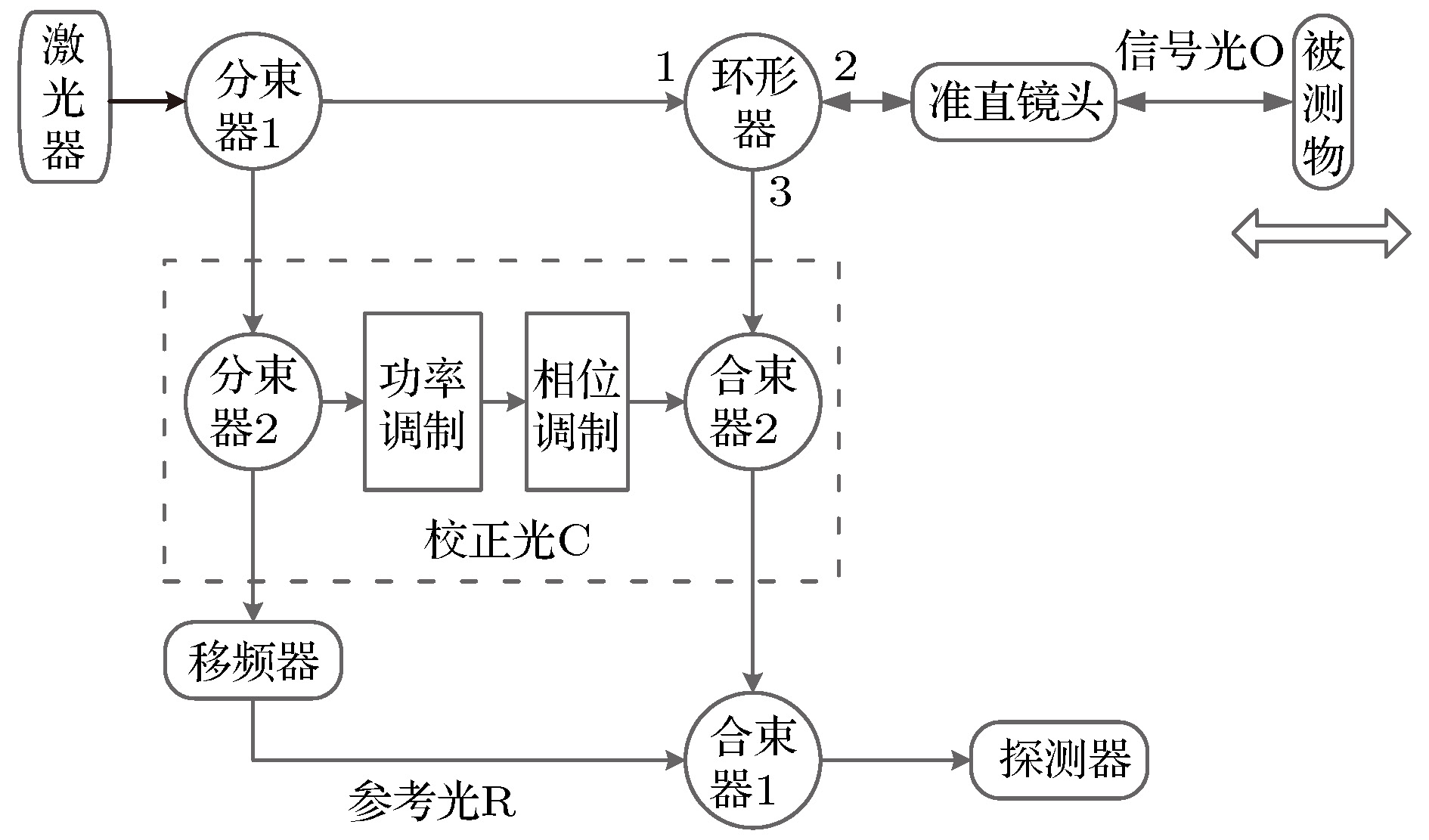
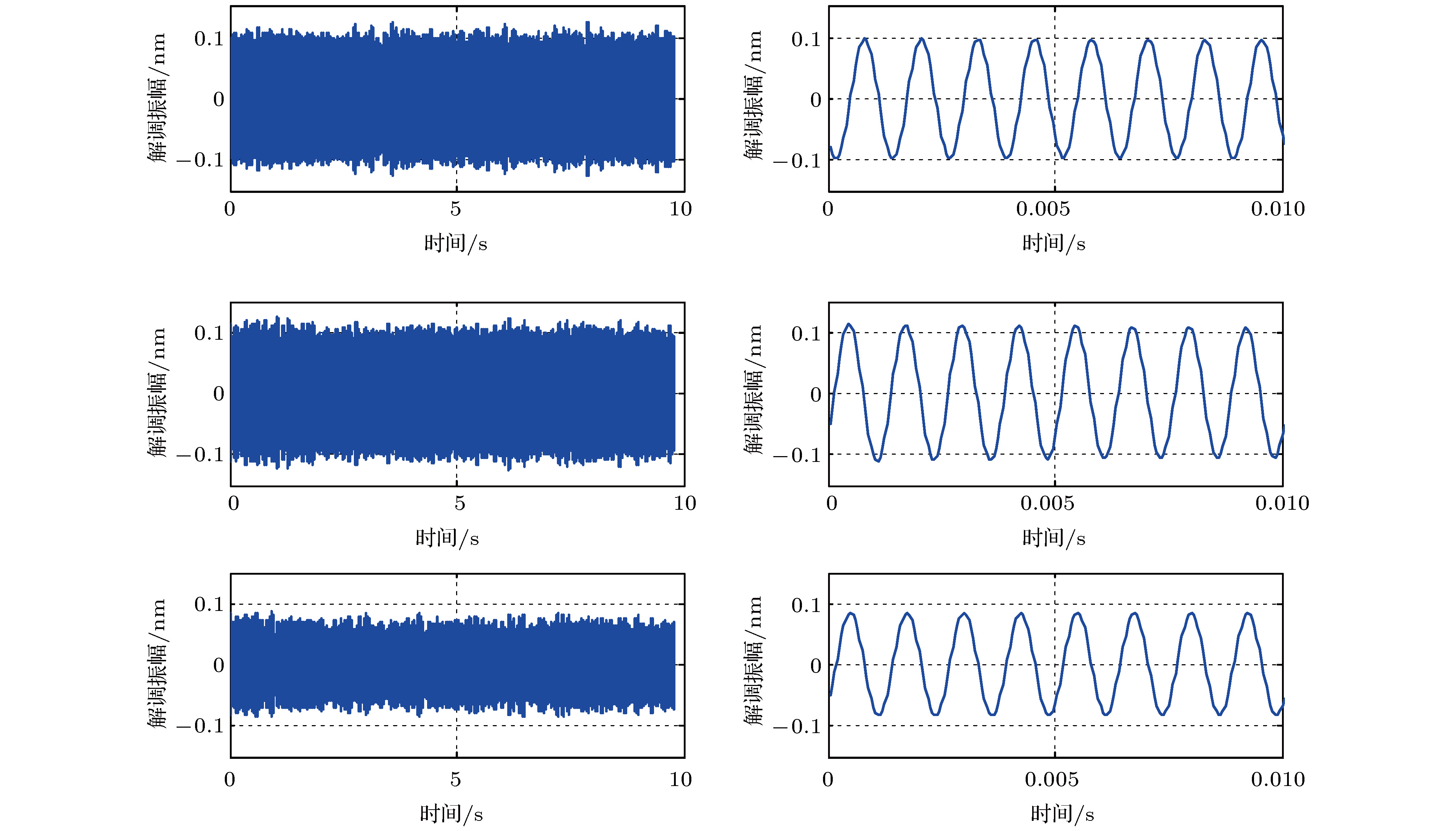
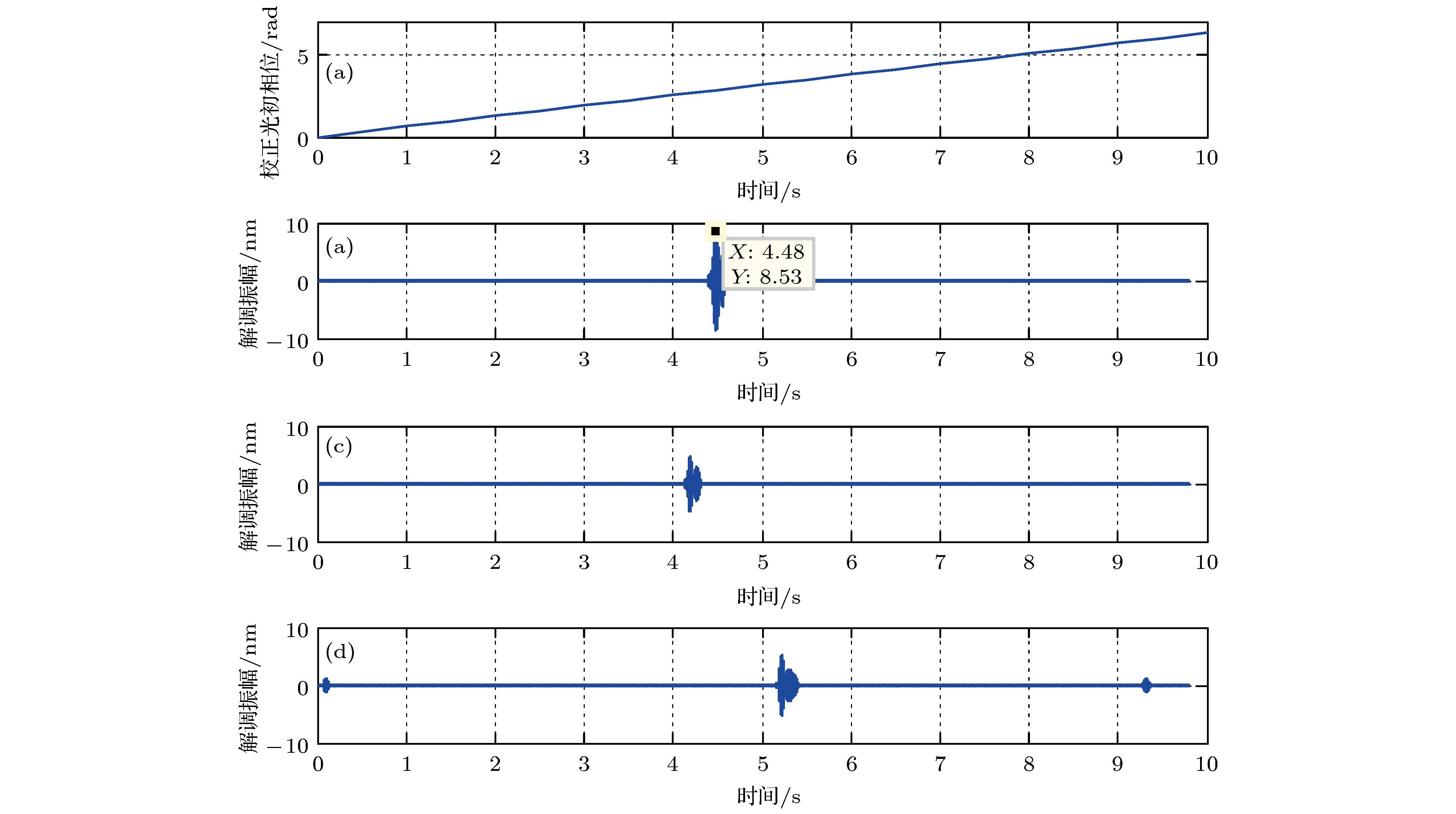
-
Laser Doppler vibrometer can measure the displacement, velocity, acceleration and other parameters of vibration target. It has the characteristics of non-contact, high precision and long distance. So, it has a great advantage for the vibration measurement in a special working environment, where the target is light and thin, hard to contact, hard to approach. Laser heterodyne interferometry is an important means of detecting the micro vibration. With the development of micro vibration application, the sensitivity of phase measurement is highly required. Traditionally, there are several ways of improving the measurement sensitivity, such as optimizing the heterodyne interference scheme, improving the phase reconstruction algorithm and reducing the noise of key devices and so on. However, based on the analysis of the influence of stray light in the system, it is found that the controllable multi-beam interference can greatly improve the detection capability of the system. Therefore, a phase enhancement technique of multi-beam hybrid interference is proposed to meet the needs of high sensitivity detection of micro vibration. In this paper the physical mechanism and boundary conditions of phase enhancement are investigated in detail, and the quantitative relationship between the boundary conditions and phase enhancement is also analyzed thereby providing a technical reference for the enhancement detection of micro vibration targets. Through the numerical simulation and experimental verification, the following boundary conditions are obtained: the initial phase difference between the correction light and the signal light is π rad and the closer the power values of the two beams, the greater the enhancement effect of the demodulation phase is. The power difference between the two beams designed in the experiment is 1%, which means that detection capability is enhanced by 146 times. It has great application value in the high sensitivity measurement of micro vibration objects. This technology can also enhance the detection capability of heterodyne interference measurement system without changing the existing device index or phase demodulation algorithm.
-
Keywords:
- heterodyne interferometry /
- Laser Doppler effect /
- phase enhancement /
- hybrid interferometry
[1] Castellini P 2006 Mech. Syst. Signal Pr. 20 1265
Google Scholar
[2] George W.K., Lumley J.L 1973 Fluid Mech. 60 321
Google Scholar
[3] Sriram, S. Hanagud, J. I. 1992 Modal Anal. 7 169
[4] Baker J R, Laming R I, Wilmshurst T H 1990 Opt. Laser Technol. 22 4 241
[5] Brunet A R, Turon P, Lacoste F. A 1985 Proc. SPIE Optics in Engineering Measurement 599 391
[6] Kong X X, Xiang L B, Zhang W X, Wu Z, Zhang D D 2019 Proc. SPIE Security Defence 111600 1
[7] Yuichi F, Daisuke, Tomohiro K, ToyohikoY 2010 Opt. Lett. 35 101548
[8] 贺寅竹, 赵世杰, 尉昊赟, 李岩 2017 66 060601
Google Scholar
He Y Z, Zhao S J, Wei H Y, Li Y 2017 Acta Phys. Sin. 66 060601
Google Scholar
[9] Jackson D A, Posada-Roman J E, Garcia-Souto J A 2015 Ele. Lett. 51 1100
Google Scholar
[10] Aranchuk V, Aranchuk I, Carpenter B, Hickey C 2019 OSA Laser Con. 4 1
[11] Li Y L, et al. 2018 OSA CLEO 5 1
[12] 杜军, 杨娜, 李峻灵, 曲彦臣, 李世明, 丁云鸿, 李锐 2018 67 064204
Google Scholar
Du J, Yang N, Li J L, Qu Y C, Li S M, Ding Y H, Li R 2018 Acta Phys. Sin. 67 064204
Google Scholar
[13] 刘亚睿 2016 硕士学位论文 (杭州: 中国计量大学)
Liu Y R 2016 M. S. Thesis (Hangzhou: China Jiliang University) (in Chinese)
[14] 党文佳 2015 博士学位论文 (西安: 西安电子科技大学)
Dang W J 2015 Ph. D. Dissertation (Xian: Xidian Univeristy) (in Chinese)
[15] Ken Y, Fumiya N 2017 Micro. opt. Conference 1 48
[16] 赵金龙 2016 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhao J L 2016 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[17] Hossam K, Dongkyu K, Joonsik N, Kyihwan P 2016 Measurement 94 883
Google Scholar
[18] 伍洲, 张文喜, 相里斌, 李杨, 孔新新 2018 67 020601
Google Scholar
Wu Z, Zhang W X, Xiang L B, Li Y, Kong X X 2018 Acta Phys. Sin. 67 020601
Google Scholar
[19] 晏春回, 王挺峰, 张合勇, 吕韬, 吴世松 2017 66 234208
Google Scholar
Yan C H, Wang T F, Zhang H Y, Lv T, Wu S S 2017 Acta Phys. Sin. 66 234208
Google Scholar
[20] Paul K, Flügge J, Weichert C 2012 Meas. Sci. Technol. 25 1
[21] Cheng Z G 2006 Appl. Opt. 45 2246
Google Scholar
[22] Lawall J 2000 Rev. of Sci. Instr. 71 2669
Google Scholar
[23] Hu P C. 2017 Opt. Exp. 25 3605
Google Scholar
[24] Yaravoi L, Siegmund G 2004 Meas. Sci. Technol. 15 2150
Google Scholar
-
图 1 典型激光外差干涉测振系统
Figure 1. Typical laser heterodyne interference vibration measurement system.
图 2 杂散光对解调振幅的影响
Figure 2. Influence of stray light on demodulation amplitude.
图 3 杂散光功率对解调振幅的影响曲线
Figure 3. Influence curve of stray light power on demodulation amplitude.
图 4 杂散光初相位对解调振幅的影响曲线
Figure 4. Influence curve of initial phase of stray light on demodulation amplitude.
图 5 三波混合干涉外差干涉测振系统
Figure 5. Three-wave hybrid interference heterodyne interference vibration measurement system.
图 6 三光束外差探测实验结构
Figure 6. Experimental structure of three-wave heterodyne detection.
图 7 无校正光下两光束干涉实验数据
Figure 7. Interference data without corrected light.
图 8 三光束混合干涉试验数据
Figure 8. Three-wave mixed interference data.
图 9 试验数据拉伸显示
Figure 9. Test data tensile display
-
[1] Castellini P 2006 Mech. Syst. Signal Pr. 20 1265
Google Scholar
[2] George W.K., Lumley J.L 1973 Fluid Mech. 60 321
Google Scholar
[3] Sriram, S. Hanagud, J. I. 1992 Modal Anal. 7 169
[4] Baker J R, Laming R I, Wilmshurst T H 1990 Opt. Laser Technol. 22 4 241
[5] Brunet A R, Turon P, Lacoste F. A 1985 Proc. SPIE Optics in Engineering Measurement 599 391
[6] Kong X X, Xiang L B, Zhang W X, Wu Z, Zhang D D 2019 Proc. SPIE Security Defence 111600 1
[7] Yuichi F, Daisuke, Tomohiro K, ToyohikoY 2010 Opt. Lett. 35 101548
[8] 贺寅竹, 赵世杰, 尉昊赟, 李岩 2017 66 060601
Google Scholar
He Y Z, Zhao S J, Wei H Y, Li Y 2017 Acta Phys. Sin. 66 060601
Google Scholar
[9] Jackson D A, Posada-Roman J E, Garcia-Souto J A 2015 Ele. Lett. 51 1100
Google Scholar
[10] Aranchuk V, Aranchuk I, Carpenter B, Hickey C 2019 OSA Laser Con. 4 1
[11] Li Y L, et al. 2018 OSA CLEO 5 1
[12] 杜军, 杨娜, 李峻灵, 曲彦臣, 李世明, 丁云鸿, 李锐 2018 67 064204
Google Scholar
Du J, Yang N, Li J L, Qu Y C, Li S M, Ding Y H, Li R 2018 Acta Phys. Sin. 67 064204
Google Scholar
[13] 刘亚睿 2016 硕士学位论文 (杭州: 中国计量大学)
Liu Y R 2016 M. S. Thesis (Hangzhou: China Jiliang University) (in Chinese)
[14] 党文佳 2015 博士学位论文 (西安: 西安电子科技大学)
Dang W J 2015 Ph. D. Dissertation (Xian: Xidian Univeristy) (in Chinese)
[15] Ken Y, Fumiya N 2017 Micro. opt. Conference 1 48
[16] 赵金龙 2016 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhao J L 2016 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[17] Hossam K, Dongkyu K, Joonsik N, Kyihwan P 2016 Measurement 94 883
Google Scholar
[18] 伍洲, 张文喜, 相里斌, 李杨, 孔新新 2018 67 020601
Google Scholar
Wu Z, Zhang W X, Xiang L B, Li Y, Kong X X 2018 Acta Phys. Sin. 67 020601
Google Scholar
[19] 晏春回, 王挺峰, 张合勇, 吕韬, 吴世松 2017 66 234208
Google Scholar
Yan C H, Wang T F, Zhang H Y, Lv T, Wu S S 2017 Acta Phys. Sin. 66 234208
Google Scholar
[20] Paul K, Flügge J, Weichert C 2012 Meas. Sci. Technol. 25 1
[21] Cheng Z G 2006 Appl. Opt. 45 2246
Google Scholar
[22] Lawall J 2000 Rev. of Sci. Instr. 71 2669
Google Scholar
[23] Hu P C. 2017 Opt. Exp. 25 3605
Google Scholar
[24] Yaravoi L, Siegmund G 2004 Meas. Sci. Technol. 15 2150
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6404
- PDF Downloads: 116
- Cited By: 0
