-
Rayleigh-Bénard (RB) convection in binary fluid mixtures, which shows rich and interesting pattern formation behavior, is a paradigm for understanding instabilities, bifurcations, self-organization with complex spatiotemporal behavior and turbulence, with many applications in atmospheric and environmental physics, astrophysics, and process technology. In this paper, by using a high-order compact finite difference method to solve the full hydrodynamic field equations, we study numerically the RB convection in binary fluid mixtures such as ethanol-water with a very weak Soret effect (separation ratio
$\psi=-0.02$ ) in a rectangular container heated uniformly from below. The direct numerical simulations are conducted in the rectangular container with aspect ratio of$\varGamma=12$ and with four no-slip and impermeable boundaries, isothermal horizontal and perfectly insulated vertical boundaries. The bifurcation and the origin and evolution of pattern in RB convection for the considered physical parameters are studied, and the bifurcation diagram is presented. By performing two-dimensional simulations, we observe three stable states of Blinking state, localized traveling wave and stationary overturning convection (SOC) state, and discuss the transitions between them. The results show that there is a hysteresis in the transition from the Blinking state to the localized traveling wave state for the considered separation ratio, and the evolution of the oscillation frequency, convection amplitude and Nusselt number are discontinuous. Near the lower bound of the Rayleigh number range where the Blinking state exists, a asymmetric initial disturbance is the inducement for the formation of the Blinking state. Inside the range, its inducing effect is weakened, and the oscillatory instability becomes the main reason. It is further confirmed that reflections of lateral walls are responsible for the survival of the stable Blinking state. With the increase of the Rayleigh number, the critical SOC state undergoes multiple bifurcations and forms multiple SOC states with different wave numbers, and then transitions to a chaotic state. There are no stable undulation traveling wave states at both ends of the critical SOC branch.-
Keywords:
- Convection /
- bifurcation /
- binary fluid mixtures /
- traveling wave
[1] Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851
Google Scholar
[2] Moses E, Fineberg J, Steinberg V 1987 Phys. Rev. A 35 2757
Google Scholar
[3] Heinrichs R, Ahlers G, Cannell D S 1987 Phys. Rev. A 35 2761
Google Scholar
[4] Fineberg J, Moses E, Steinberg V 1988 Phys. Rev. Lett. 61 838
Google Scholar
[5] Kolodner P, Surko C M 1988 Phys. Rev. Lett. 61 842
Google Scholar
[6] Barten W, Lücke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5636
Google Scholar
[7] Barten W, Lücke M, Kamps M 1991 Phys. Rev. Lett. 66 2621
Google Scholar
[8] Barten W, Lücke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5662
Google Scholar
[9] Batiste O, Net M, Mercader I, Knobloch E 2001 Phys. Rev. Lett. 86 2309
Google Scholar
[10] Batiste O, Knobloch E 2005 Phys. Rev. Lett. 95 244501
Google Scholar
[11] Ning L Z 2006 Rayleigh-Bénard convection in a binary fluid mixture with and without lateral flow (Xi’an: Northwest A&F University Press) pp41–56
[12] 李国栋, 黄永念 2007 56 4742
Google Scholar
Li G D, Huang Y N 2007 Acta Phys. Sin. 56 4742
Google Scholar
[13] 宁利中, 齐昕, 周洋, 余荔 2009 58 2528
Google Scholar
Ning L Z, Qi X, Zhou Y, Yu L 2009 Acta Phys. Sin. 58 2528
Google Scholar
[14] Mercader I, Batiste O, Alonso A, Knobloch E 2011 J. Fluid Mech. 667 586
Google Scholar
[15] Mercader I, Batiste O, Alonso A, Knobloch E 2013 J. Fluid Mech. 722 240
Google Scholar
[16] 王涛, 田振夫, 葛永斌 2011 水动学研究与进展(A辑) 26 41
Wang T, Tian Z F, Ge Y B 2011 Chin. J. Hydrodyn. 26 41
[17] Watanabe T, Iima M, Nishiura Y 2012 J. Fluid Mech. 712 219
Google Scholar
[18] Taraut A V, Smorodin B L, Lücke M 2012 New J. Phys. 14 093055
Google Scholar
[19] 赵秉新 2012 水动力学研究与进展(A辑) 27 264
Zhao B X 2012 Chin. J. Hydrodyn. 27 264
[20] Shevtsova V, Gaponenko Y A, Sechenyh V, Melnikov D E, Lyubimova T, Mialdun A 2015 J. Fluid Mech. 767 290
Google Scholar
[21] Lyubimova T, Zubova N, Shevtsova V 2018 Microgravity Sci. Tec. 31 1
[22] Alonso A, Mercader I, Batiste O 2018 Phys. Rev. E 97 023108
Google Scholar
[23] Smorodin B L, Ishutov S M, Myznikova B I 2017 Microgravity Sci. Technol. 30 95
[24] Zhao B X, Tian Z F 2015 Phys. Fluids 27 074102
Google Scholar
[25] Mercader I, Batiste O, Alonso A, Knobloch E 2019 Phys. Rev. E 99 023113
Google Scholar
[26] Lyubimova T, Zubova N 2017 Int. J. Heat Mass Transfer 106 1134
Google Scholar
[27] 宁利中, 刘爽, 宁碧波, 袁喆, 王新宏, 田伟利, 渠亚伟 2018 水动力学研究与进展(A辑) 33 515
Ning L Z, Liu S, Ning B B, Tian W L, Qu Y W 2018 Chin. J. Hydrodyn. 33 515
[28] 宁利中, 徐泊冰, 宁碧波, 袁喆, 田伟利 2019 水动力学研究与进展(A辑) 34 93
Ning L Z, Xu B B, Ning B B, Yuan Z, Tian W L 2019 Chin. J. Hydrodyn. 34 93
[29] 宁利中, 余荔, 袁喆, 周洋 2009 中国科学: 物理学 力学 天文学 39 746
Ning L Z, Yu L, Yuan Z, Zhou Y 2009 Sci. Sin.-Phys. Mech. Astron. 39 746
[30] 宁利中, 王娜, 袁喆, 李开继, 王卓运 2014 63 104401
Google Scholar
Ning L Z, Wang N, Yuan Z, Li K J, Wang Z Y 2014 Acta Phys. Sin. 63 104401
Google Scholar
[31] Qin Q, Xia Z A, Tian Z F 2014 Int. J. Heat Mass Transfer 71 405
Google Scholar
[32] Tian Z F, Liang X, Yu P X 2011 Int. J. Numer. Meth. Een. 88 511
Google Scholar
[33] Strogatz S H 1994 Nonlinear Dynamics and Chaos: With Applications To Physics, Biology, Chemistry, and Engineering (New York: Perseus Books Publishing LLC) pp58–60
[34] Dangelmayr G, Knobloch E, Wegelin M 1991 EPL-Europhys. Lett. 16 723
Google Scholar
-
图 1 对流模型示意图
Figure 1. Sketch of the two-dimensional convection model
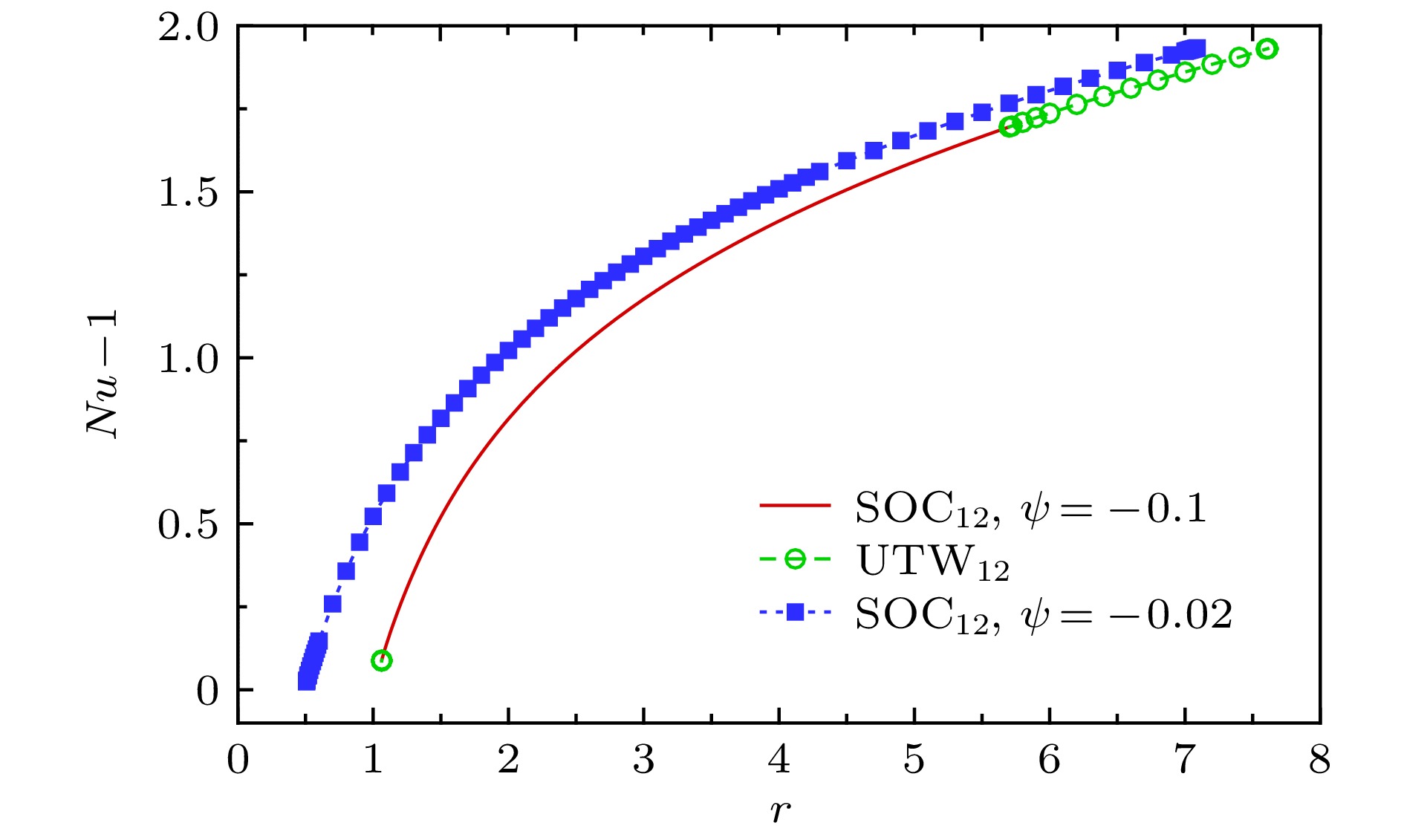
图 2
$ \psi=-0.02 $ 时Nusselt数$ Nu-1 $ 关于Rayleigh数r的分岔曲线. SOC$ _n $ 表示具有n个涡卷的SOC状态Figure 2. (a) Bifurcation diagram for
$ \psi=-0.02 $ . (b) close-up view of the part of the bifurcation diagram delimited by the straight dashed lines depicted in (a). Where SOC$ _n $ represents the SOC solutions with n rolls
图 3
$ r=1.015 $ 时 (a) 流场时空结构, (b)$ w(0.13\varGamma, 0.5) $ 的时间序列和(c)功率谱密度Figure 3. (a) Spatio-temporal structure, (b) the time series of
$ w(0.13\varGamma, 0.5) $ and (c) power spectral density for$ r=1.015 $ 
图 4
$ r=1.015 $ 时, 两个观测点处垂向速度w随时间的发展Figure 4. The time series of the vertical velocity w at two monitoring points (a)
$ (0.13\varGamma, 0.5) $ and (b)$ (0.87\varGamma, 0.5) $ for$ r=1.015 $ 
图 5
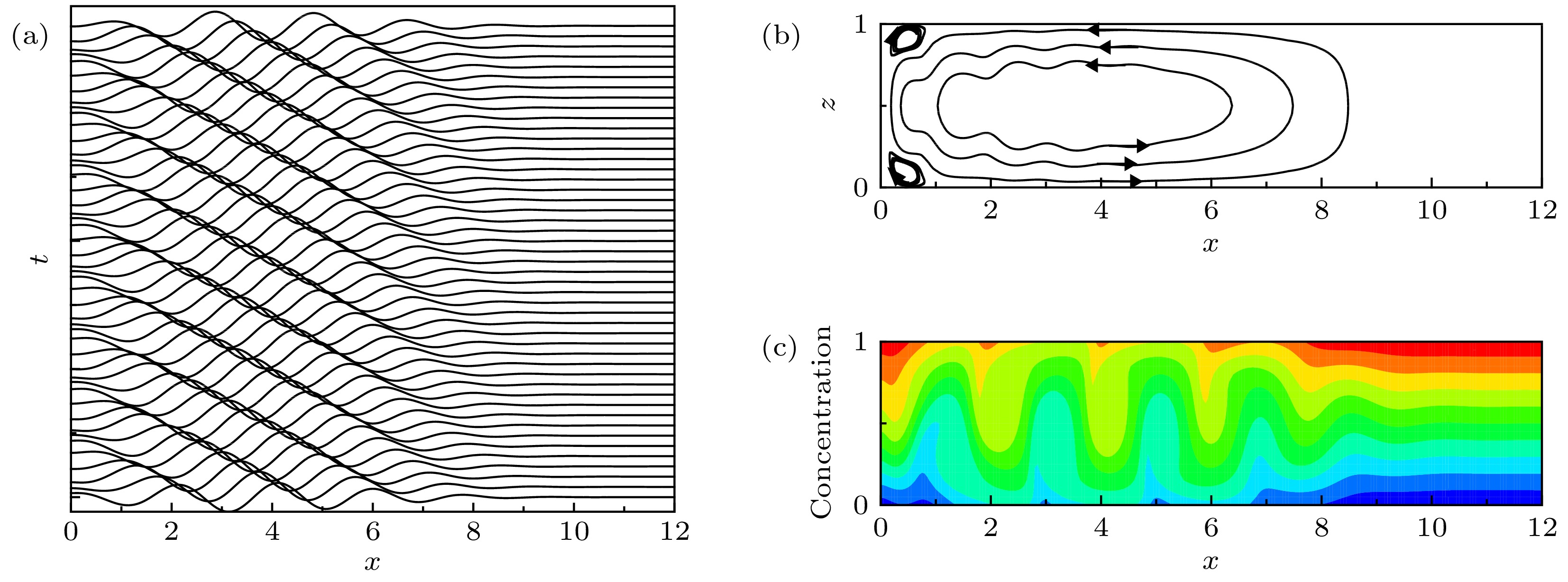
$ r=1.0171 $ 时, Blinking状态与LTW状态流场典型波形和浓度场的比较Figure 5. Comparison of the lateral profiles and concentration fields between the Blinking and LTW states at
$ r=1.0171 $ : (a) The lateral profile and (c) concentration field of the Blinking state; (b) The lateral profile and (d) concentration field of the LTW state
图 6 (a)闪动频率
$ \omega_1 $ 和(b)行波频率$ \omega_2 $ 随Rayleigh数的变化Figure 6. The variation of (a) blinking frequency
$ \omega_1 $ and (b) oscillation frequency$ \omega_2 $ as a function of the Rayleigh number
图 7 Blinking和LTW状态的
$ Nu-1 $ 随r的变化情况. (b)为(a)中虚线标注矩形区域的局部放大Figure 7. The variation of
$ Nu-1 $ of the Blinking and LTW states as a function of r. (b) Close-up view of the part delimited by the straight dashed lines depicted in (a)
图 8 LTW状态的流场结构
Figure 8. Structures of the flow field of LTW state: (a) Spatio-temporal structure; (b) a large-scale concentration current; (c) a transient structure of the concentration field
图 9
$ r=1.13 $ 时流场时空发展和典型时刻的瞬时结构Figure 9. The spatio-temporal development and transient structures of the flow field at typical times for
$ r=1.13 $ 
图 10
$ r=1.13 $ 时 (a)$ Nu-1 $ 和M的变化及(b)观测点处垂向速度的时间序列Figure 10. The variation of (a)
$ Nu-1 $ , M, and (b) the vertical velocity at the monitoring points for$ r=1.13 $ 
图 11
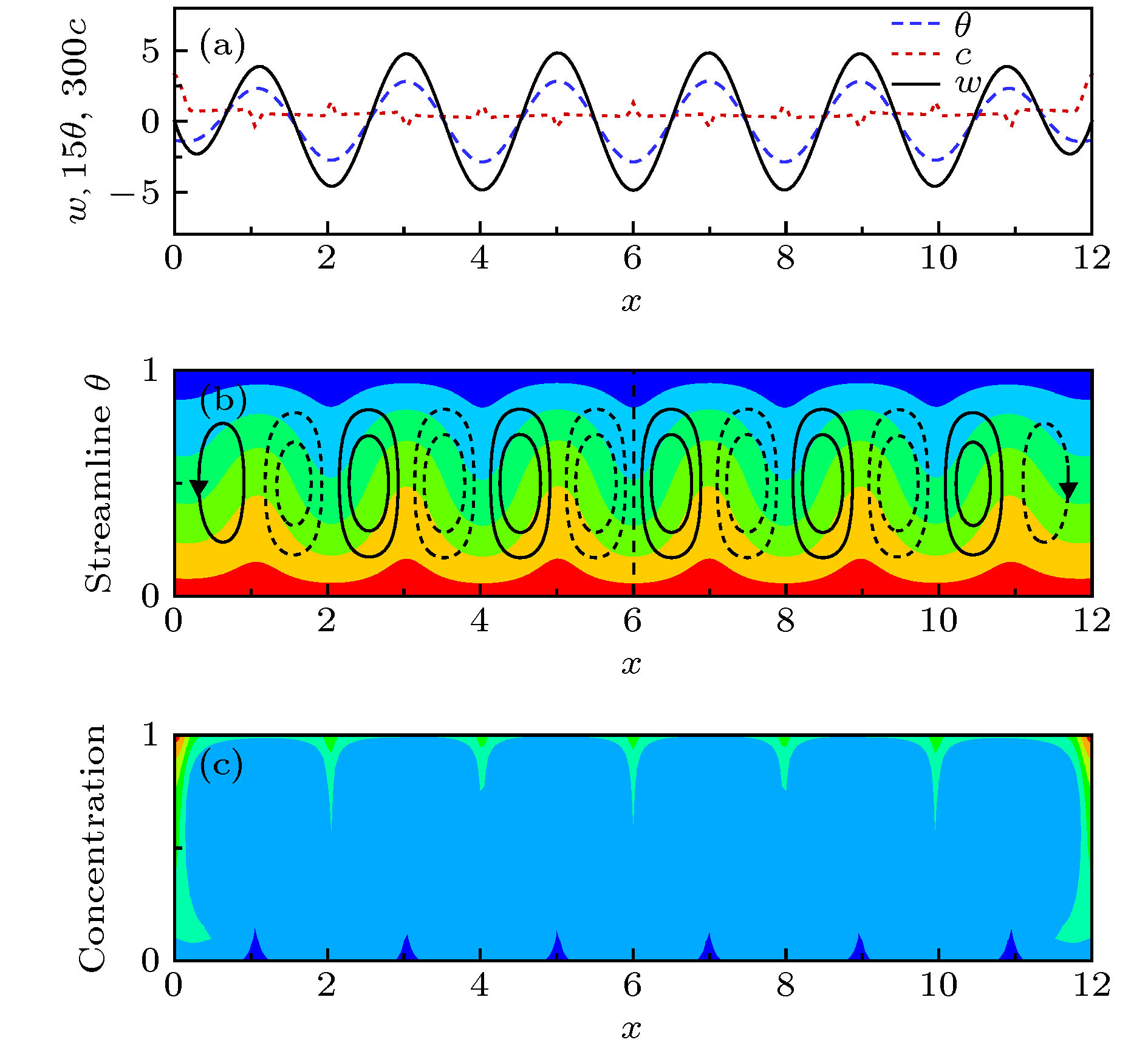
$ r=1.13 $ 时SOC$ _{12} $ 状态的流场结构Figure 11. The structure of flow field for the SOC
$ _{12} $ state at$ r=1.13 $ : (a) The lateral profile on the horizontal centerline of the cavity; (b) the streamlines and the structure of the associated temperature field; (c) the structure of the concentration field
图 12 SOC
$ _{12} $ 状态Nusselt数随Rayleigh数的变化Figure 12. The variation of
$ Nu $ with r for the SOC$ _{12} $ state表 1 分离比
$ \psi = -0.10 $ 和–0.02时, 各状态临界Rayleigh数的比较Table 1. Comparison of critical Rayleigh numbers for each state,
$ \psi = -0.10 $ and$ -0.02 $ $ \psi $ $ r_{\rm c} $ $ r_{\rm {sn}}^{\rm {SOC}} $ $ r_{\rm {start}}^{\rm {BTW}} $ $ r_{\rm {start}}^{\rm {LTW}} $ $ r^* $ –0.10 1.111 1.062 — 1.089 1.145 –0.02 1.035 1.008 1.013 1.0172 1.022 
DownLoad: CSV
-
[1] Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851
Google Scholar
[2] Moses E, Fineberg J, Steinberg V 1987 Phys. Rev. A 35 2757
Google Scholar
[3] Heinrichs R, Ahlers G, Cannell D S 1987 Phys. Rev. A 35 2761
Google Scholar
[4] Fineberg J, Moses E, Steinberg V 1988 Phys. Rev. Lett. 61 838
Google Scholar
[5] Kolodner P, Surko C M 1988 Phys. Rev. Lett. 61 842
Google Scholar
[6] Barten W, Lücke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5636
Google Scholar
[7] Barten W, Lücke M, Kamps M 1991 Phys. Rev. Lett. 66 2621
Google Scholar
[8] Barten W, Lücke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5662
Google Scholar
[9] Batiste O, Net M, Mercader I, Knobloch E 2001 Phys. Rev. Lett. 86 2309
Google Scholar
[10] Batiste O, Knobloch E 2005 Phys. Rev. Lett. 95 244501
Google Scholar
[11] Ning L Z 2006 Rayleigh-Bénard convection in a binary fluid mixture with and without lateral flow (Xi’an: Northwest A&F University Press) pp41–56
[12] 李国栋, 黄永念 2007 56 4742
Google Scholar
Li G D, Huang Y N 2007 Acta Phys. Sin. 56 4742
Google Scholar
[13] 宁利中, 齐昕, 周洋, 余荔 2009 58 2528
Google Scholar
Ning L Z, Qi X, Zhou Y, Yu L 2009 Acta Phys. Sin. 58 2528
Google Scholar
[14] Mercader I, Batiste O, Alonso A, Knobloch E 2011 J. Fluid Mech. 667 586
Google Scholar
[15] Mercader I, Batiste O, Alonso A, Knobloch E 2013 J. Fluid Mech. 722 240
Google Scholar
[16] 王涛, 田振夫, 葛永斌 2011 水动学研究与进展(A辑) 26 41
Wang T, Tian Z F, Ge Y B 2011 Chin. J. Hydrodyn. 26 41
[17] Watanabe T, Iima M, Nishiura Y 2012 J. Fluid Mech. 712 219
Google Scholar
[18] Taraut A V, Smorodin B L, Lücke M 2012 New J. Phys. 14 093055
Google Scholar
[19] 赵秉新 2012 水动力学研究与进展(A辑) 27 264
Zhao B X 2012 Chin. J. Hydrodyn. 27 264
[20] Shevtsova V, Gaponenko Y A, Sechenyh V, Melnikov D E, Lyubimova T, Mialdun A 2015 J. Fluid Mech. 767 290
Google Scholar
[21] Lyubimova T, Zubova N, Shevtsova V 2018 Microgravity Sci. Tec. 31 1
[22] Alonso A, Mercader I, Batiste O 2018 Phys. Rev. E 97 023108
Google Scholar
[23] Smorodin B L, Ishutov S M, Myznikova B I 2017 Microgravity Sci. Technol. 30 95
[24] Zhao B X, Tian Z F 2015 Phys. Fluids 27 074102
Google Scholar
[25] Mercader I, Batiste O, Alonso A, Knobloch E 2019 Phys. Rev. E 99 023113
Google Scholar
[26] Lyubimova T, Zubova N 2017 Int. J. Heat Mass Transfer 106 1134
Google Scholar
[27] 宁利中, 刘爽, 宁碧波, 袁喆, 王新宏, 田伟利, 渠亚伟 2018 水动力学研究与进展(A辑) 33 515
Ning L Z, Liu S, Ning B B, Tian W L, Qu Y W 2018 Chin. J. Hydrodyn. 33 515
[28] 宁利中, 徐泊冰, 宁碧波, 袁喆, 田伟利 2019 水动力学研究与进展(A辑) 34 93
Ning L Z, Xu B B, Ning B B, Yuan Z, Tian W L 2019 Chin. J. Hydrodyn. 34 93
[29] 宁利中, 余荔, 袁喆, 周洋 2009 中国科学: 物理学 力学 天文学 39 746
Ning L Z, Yu L, Yuan Z, Zhou Y 2009 Sci. Sin.-Phys. Mech. Astron. 39 746
[30] 宁利中, 王娜, 袁喆, 李开继, 王卓运 2014 63 104401
Google Scholar
Ning L Z, Wang N, Yuan Z, Li K J, Wang Z Y 2014 Acta Phys. Sin. 63 104401
Google Scholar
[31] Qin Q, Xia Z A, Tian Z F 2014 Int. J. Heat Mass Transfer 71 405
Google Scholar
[32] Tian Z F, Liang X, Yu P X 2011 Int. J. Numer. Meth. Een. 88 511
Google Scholar
[33] Strogatz S H 1994 Nonlinear Dynamics and Chaos: With Applications To Physics, Biology, Chemistry, and Engineering (New York: Perseus Books Publishing LLC) pp58–60
[34] Dangelmayr G, Knobloch E, Wegelin M 1991 EPL-Europhys. Lett. 16 723
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6929
- PDF Downloads: 84
- Cited By: 0
