-
位于新生和成年哺乳动物延髓腹外侧区的前包钦格复合体被认为是呼吸节律产生的中枢. 正常状态下呼吸节律是均匀而整齐的, 而病理状态下呼吸节律会发生变化, 因此研究呼吸节律产生的动力学机制及其控制有重要意义. 本文基于前包钦格复合体中胞体-树突耦合神经元模型, 利用相平面分析、分岔分析、快慢动力学分析以及ISI (峰峰间期)分岔序列等方法, 研究了在钙离子动力学及LIP3 (内质网泄漏渗透率)的影响下, LIP3的变化对耦合前包钦格复合体神经元放电节律的重要影响, 并研究了模型中反相簇放电的模式及其转迁机制. 结果表明, 钙的周期性波动是混合簇放电产生的关键因素, 但不是混合簇放电产生的必要条件. 本文的研究方法也可以应用于其他多时间尺度的神经系统中.The pre-Bötzinger complex, which is located at a ventrolateral medulla of human and mammal, is considered to be the center for the generation of respiratory rhythms. In a normal state, the respiratory rhythm is uniform and orderly. Otherwise, the respiratory rhythm will change to a pathological state. Therefore, the monitoring of respiratory rhythm is of great significance in monitoring the health. In this paper, according to a two-coupled model of pre-Bötzinger complex with calcium ion current, we investigate the generation and transition mechanism of anti-phase bursting synchronization by using phase-plane analysis, bifurcation and fast-slow decomposition. It is found that the pre-Bötzinger complex model can exhibit mixed bursting when calcium ion concentration is at steady state, which indicates that the oscillation of calcium is not a necessary condition for the generation of mixed bursting. This is quite different from the results obtained in previous studies, indicating that the mixed bursting is caused by the periodic fluctuations of calcium. The methods used in this paper can provide a new idea for investigating the dynamics of mixed bursting, and it can also be applied to the study of other neuronal systems on a multiple time scale.
-
Keywords:
- pre-Bötzinger complex /
- mixed bursting /
- bifurcation /
- fast-slow analysis
[1] Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726
Google Scholar
[2] Jens C, Rekling, Jack L, Feldman 1998 Annu. Rev. Physiol. 60 385
Google Scholar
[3] Gourévitch B, Mellen N 2014 Neuroimage 98 460
Google Scholar
[4] Lieske S P, Thoby-Brisson M, Telgkamp P, Ramirez J M 2000 Nat. Neurosci. 3 600
Google Scholar
[5] Naughton M T 2012 Thorax 67 357
Google Scholar
[6] Spiesshoefer J 2019 Int. J. Cardiol. 289 99
Google Scholar
[7] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[8] Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 382
Google Scholar
[9] Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 398
Google Scholar
[10] Kosmidis E K 2004 J. Neurophysiol. 92 686
Google Scholar
[11] Smith J C, Abdala A P L, Koizumi H, Rybak I A, Paton J F R 2007 J. Neurophysiol. 98 3370
Google Scholar
[12] Rubin J E, Hayes J A, Mendenhall J L, Del Negro C A 2009 Proc. Natl. Acad. Sci. U.S.A. 106 2939
Google Scholar
[13] Toporikova N, Butera R J 2011 J. Comput. Neurosci. 30 515
Google Scholar
[14] Park C, Rubin J E 2013 J. Comput. Neurosci. 34 345
Google Scholar
[15] Duan L X, Yuan D D, Chen X, Meng X Y 2015 Int. J. Bifurcation Chaos 25 1550069
Google Scholar
[16] 埃门创特 B 著 (吴莹, 刘深泉 译) 2010 神经科学的数学基础 (北京: 高等教育出版社) 第95−117页
Ermentrout B G, Terman D H (translated by Wu Y, Liu S Q) 2010 The Mathematical Foundations of Neuroscience (Beijing: Higher Education Press) pp95−117 (in Chinese)
[17] 尤里 · 阿 · 库兹涅佐夫 著 (金成桴 译) 2004 应用分支理论基础 (北京: 科学出版社) 第68−104页
Kuznetsov Y A (translated by Jin C F) 2004 Elements of Applied Bifurcation Theory (Beijing: Science Press) pp68−104 (in Chinese)
[18] Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171
Google Scholar
[19] Wang Y, Rubin J E 2016 J. Comput. Neurosci. 41 245
Google Scholar
[20] Lü Z S, Chen L N, Duan L X 2019 Appl. Math. Modell. 67 234
Google Scholar
[21] 王付霞, 谢勇 2013 62 020509
Google Scholar
Wang F X, Xie Y 2013 Acta Phys. Sin. 62 020509
Google Scholar
[22] Best J, Borisyuk A, Rubin J E, Terman D, Wechselberger M 2005 SIAM J. Appl. Dyn. Syst. 4 1107
Google Scholar
[23] Wang Z J, Duan L X, Cao Q Y 2018 Chin. Phys. B 27 070502
Google Scholar
[24] 杨永霞, 李玉叶, 古华光 2020 69 040501
Google Scholar
Yang Y X, Li Y Y, Gu H G 2020 Acta Phys. Sin. 69 040501
Google Scholar
[25] Morita K, Koketsu K, Kuba K 1980 Nature 283 204
Google Scholar
[26] Wang S Y, Ma X D, Yan F, Peng H X, Zheng C D, Bai C W 2004 China J. Mod. Med. 14 49
Google Scholar
[27] Goldbeter A, Dupont G 1990 Biophys. Chem. 37 341
Google Scholar
[28] Jouaville L S, lchas F, Holmnhamedov E L 1995 Nature 377 438
Google Scholar
[29] Falcke M, Hudson J L, Camacho P, Lechleiter J D 1999 Biophys. J. 77 37
Google Scholar
[30] 施小民 2003 博士学位论文 (上海: 上海大学)
Shi X M 2003 Ph. D. Dissertation (Shanghai: Shanghai University) (in Chinese)
[31] 马芬, 段利霞, 梁桐桐, 梁王娟, 赵勇 2020 动力学与控制学报 18 82
Google Scholar
Ma F, Duan L X, Liang T T, Liang W J, Zhao Y 2020 J. Dyn. Control 18 82
Google Scholar
[32] 埃门创特 B 著 (孝鹏程, 段利霞, 苏建忠 译) 2002 动力系统仿真, 分析与动画——XPPAUT使用指南 (北京: 科学出版社) 第155−167页
Ermentrout B (translated by Xiao P C, Duan L L, Su J Z) 2002 Simulating, Analyzing, and Animating Dynamical Systems : A Guide to XPPAUT for Researchers and Students (Beijing: Science Press) pp155−167 (in Chinese)
[33] Duan L X, Liu J, Chen X, Xiao P C, Zhao Y 2017 Cogn. Neurodyn. 11 91
Google Scholar
-
图 1 参数
${L_{{\rm{I}}{{\rm{P}}_3}}}$ 变化时树突子系统(方程(5)和方程(6))的动力学 (a)$ [{{\rm{IP}} _3}] = 1.2 \; {\rm{{\text{μ}} mol/L}} $ 时的单参数分岔, 其中黑色曲线表示平衡点, 红色曲线表示周期轨道的最大值和最小值;${{\rm{F}}_1}$ ,${{\rm{F}}_{\rm{2}}}$ 表示平衡点的鞍结分岔;${\rm{HB}}$ 表示Hopf分岔; (b) 极限环的变化周期; (c) 极限环的变化频率. 参数值见附录AFig. 1. Dynamics of the dendritic subsystem with parameter
${L_{{\rm{I}}{{\rm{P}}_3}}}$ : (a) One-parameter bifurcation of dendritic subsystem with$ [{{\rm{IP}} _3}] = 1.2 \; {\rm{{\text{μ}} mol/L}} $ . Black curve indicates equilibrium points and red curve indicates maximum and minimum values of periodic orbits respectively.${\operatorname{F} _1}$ and${\operatorname{F} _2}$ are the fold bifurcation points,${\rm{HB}}$ is the Hopf bifurcation. (b) Changes of period of limit cycle with the parameter${L_{{\rm{I}}{{\rm{P}}_3}}}$ . (c) Changes of frequency of limit cycle with the parameter${L_{{\rm{I}}{{\rm{P}}_3}}}$ . Defaulted parameter values are shown in Appendix A.
图 2 树突子系统 (方程(5)和方程(6))的动力学分析 (a) 单参数分岔, 其中
$ [{\rm{I}}{{\rm{P}}_3}] = 1, 1.05, 1.1, 1.2 \; {\rm{{\text{μ}} mol/L}} $ ; (b)$({L_{{\rm{I}}{{\rm{P}}_3}}}, $ $ [{{\rm{IP}} _3}])$ 平面上的双参数分岔, 分岔曲线包括平衡点的鞍结分岔($f$ ), Hopf分岔(hb)和不变圆上的鞍结分岔($snic$ ); (c) 图(b)的部分放大图Fig. 2. Dynamics analysis of the dendritic subsystem: (a) One-parameter bifurcation with
$ [{\rm{I}}{{\rm{P}}_3}] = 1, 1.05, 1.1, 1.2 \; {\rm{{\text{μ}} mol/L}} $ , respectively. (b) Two-parameter bifurcation with$[{{\rm{IP}} _3}]$ and${L_{{\rm{I}}{{\rm{P}}_3}}}$ as parameters. The bifurcation curves represent fold bifurcation ($f$ ), Hopf bifurcation (hb) and the saddle-node on invariant circle bifurcation ($snic$ ) of equilibrium points. (c) Enlargement part of panel (b).
图 3 反相簇放电模式 (a)
$ {L}_{{\rm{IP}}_{3}}=0\;{\rm{PL}}\cdot {\rm{s}}^{-1}$ ; (b)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.1\; {\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (c)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.4\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (d)$ {L}_{{\rm{IP}}_{3}}=0.5\;{\rm{PL}}\cdot {\rm{s}}^{\rm{-1}}$ ; (e)${L}_{{\rm{IP}}_{3}}= $ $ 3\;{\rm{PL}}\cdot {\rm{s}}^{-1}$ ; (f)${L_{{\rm{I}}{{\rm{P}}_3}}} = 15\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ Fig. 3. Anti-phase bursting of the system: (a)
$ {L}_{{\rm{IP}}_{3}}=0\;{\rm{PL}}\cdot {\rm{s}}^{\rm{-1}}$ ; (b)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.1\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (c)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.4 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (d)${L}_{{\rm{IP}}_{3}}= $ $ 0.5\;{\rm{PL}}\cdot {\rm{s}}^{\rm{-1}}$ ; (e)$ {L}_{{\rm{IP}}_{3}}=3\;{\rm{PL}}\cdot {\rm{s}}^{\rm{-1}}$ ; (f)${L_{{\rm{I}}{{\rm{P}}_3}}} = 15\; {\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ .
图 4 (a)
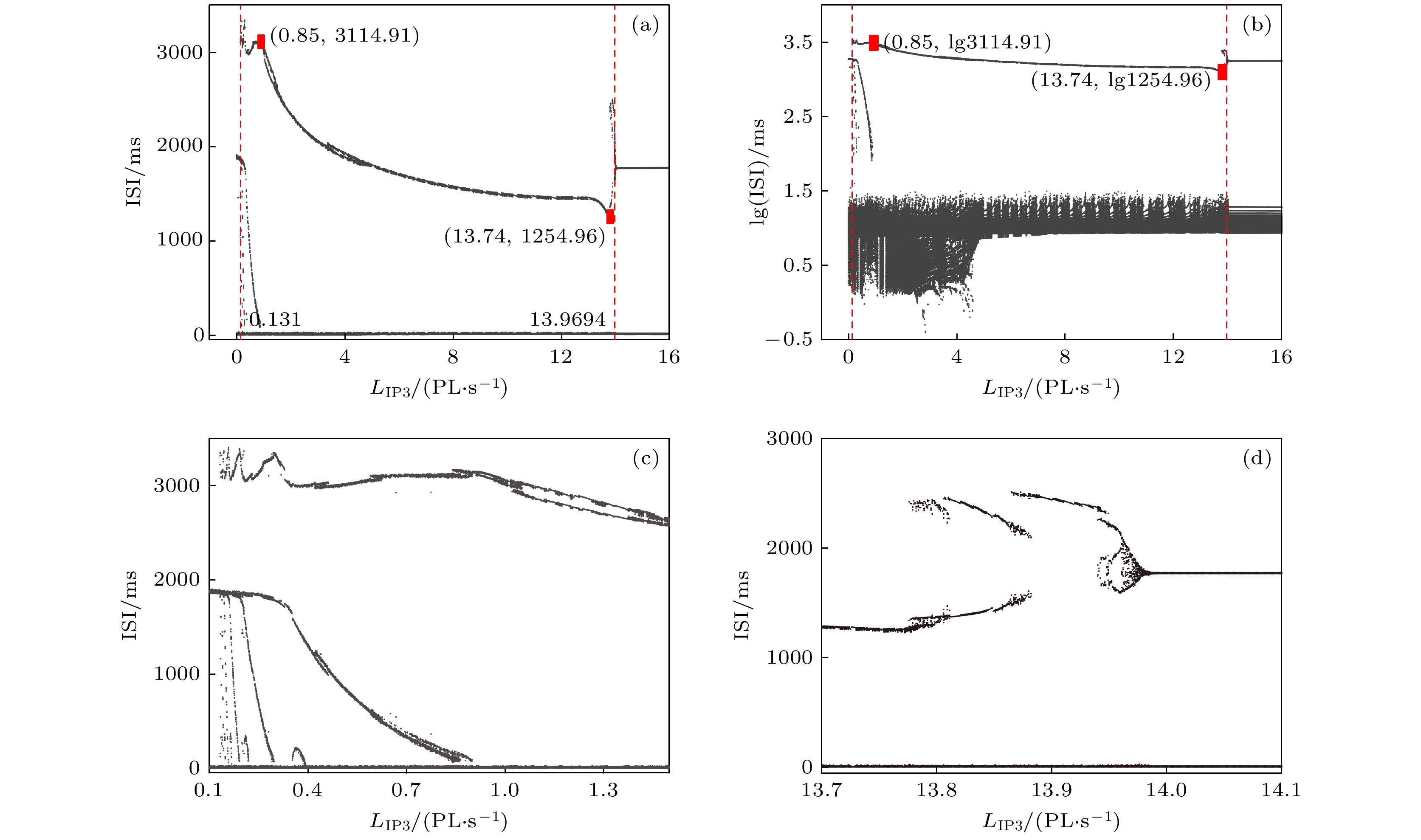
${L_{{\rm{I}}{{\rm{P}}_3}}}$ 变化时膜电位$ {V}_{1} $ 对应的${\rm{ISI}}$ 分岔序列; (b) 纵坐标${\rm{ISI}}$ 取对数对应的分岔图; (c), (d) 图(a)的部分放大图Fig. 4. (a)
${\rm{ISI}}$ diagram of membrane potential${V_1}$ with parameter${L_{{\rm{I}}{{\rm{P}}_3}}}$ ; (b) logarithm as ordinate of${\rm{ISI}}$ for panel (a); (c), (d) partially enlarged diagram of panel (a).
图 5 反相簇放电的快慢分岔分析 (a), (b)
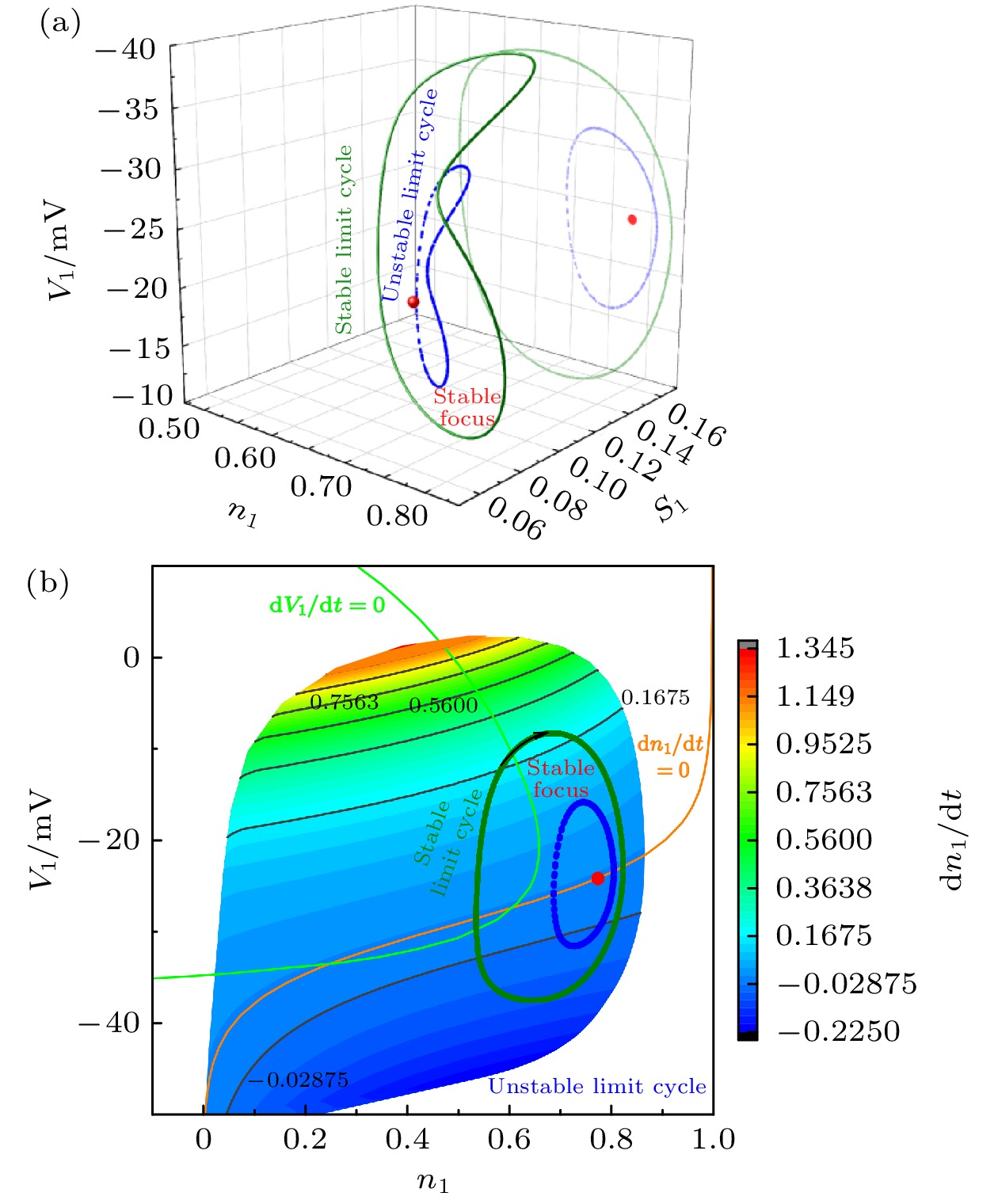
${L_{{\rm{I}}{{\rm{P}}_3}}} = 0 \;{\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (c), (d)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.1 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (e)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.4 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (f)${L_{{\rm{I}}{{\rm{P}}_3}}} = $ $ 0.5 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ Fig. 5. Fast-slow bifurcation analysis of anti-phase bursting with (a), (b)
${L_{{\rm{I}}{{\rm{P}}_3}}} = 0\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (c), (d)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.1\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (e)${L_{{\rm{I}}{{\rm{P}}_3}}} = $ $ 0.4 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (f)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.5 \;{\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ .
图 6
${L_{{\rm{I}}{{\rm{P}}_3}}} $ 取不同值时反相簇放电的双参数$({h_1}, \; {g_{{\rm{CA}}{{\rm{N}}_{{\rm{Tot}}1}}}})$ 分岔分析 (a)${L_{{\rm{I}}{{\rm{P}}_3}}} = $ $ 0.4\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (b)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.5 \;{\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (c)${L_{{\rm{I}}{{\rm{P}}_3}}} = 3 \;{\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ Fig. 6. Two-parameter bifurcation of the anti-phase bursting in
$({h_1}, \; {g_{{\rm{CA}}{{\rm{N}}_{{\rm{Tot}}1}}}})$ -plane with different$ {L_{{\rm{I}}{{\rm{P}}_3}}} $ : (a)${L_{{\rm{I}}{{\rm{P}}_3}}} = $ $ 0.4\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ; (b)${L_{{\rm{I}}{{\rm{P}}_3}}} = 0.5\; {\rm{PL}} \cdot {{\rm{s}}^{{\rm{ - 1}}}}$ ; (c)${L_{{\rm{I}}{{\rm{P}}_3}}} = 3\; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ .
图 7 (a)
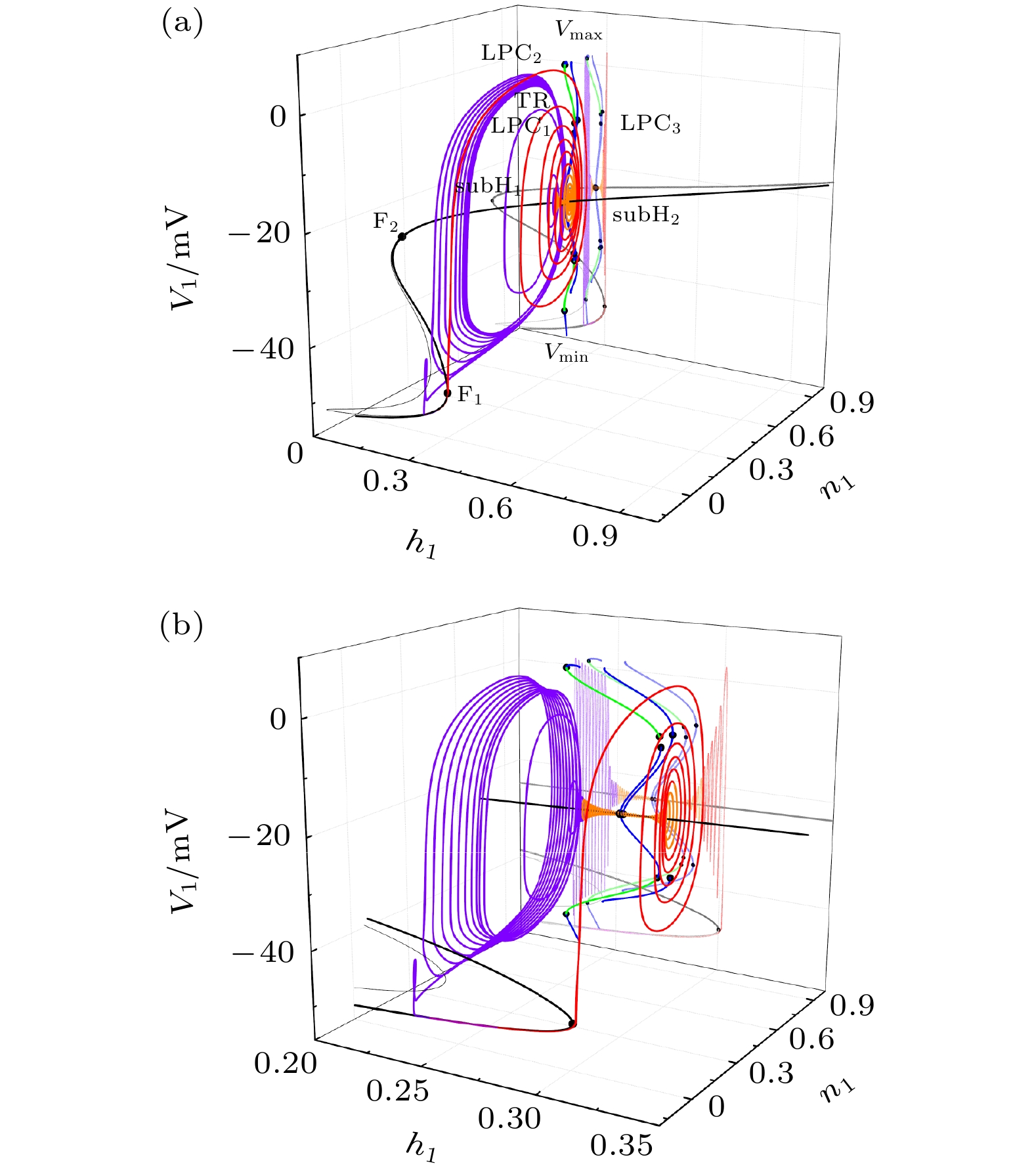
$ {L}_{{\rm{IP}}_{3}}=0\;{\rm{PL}}\cdot {\rm{s}}^{-1}$ 时反相簇放电的快子系统在$({h_1}, {n_1}, {V_1})$ 空间中的分岔结构图; (b) 图(a)的部分放大Fig. 7. (a) Bifurcation structure of the fast subsystem of anti-phase bursting in
$({h_1}, {n_1}, {V_1})$ space with${L}_{{\rm{IP}}_{3}}= $ $ 0\;{\rm{PL}}\cdot {\rm{s}}^{-1}$ ; (b) partial enlargement of panel (a).
图 8
${h_1} = 0.279$ 时, 系统的稳定焦点、稳定和不稳定的极限环 (a)$({n_1}, {s_1}, {V_1})$ 空间; (b)$({n_1}, {V_1})$ 平面Fig. 8. Stable focus, stable and unstable limit cycle in (a)
$({n_1}, {s_1}, {V_1})$ -space, (b)$({n_1}, {V_1})$ -plane.表 1 不同
$[{{\rm{IP}} _3}]$ 下树突子系统中关键点的${L_{{\rm{I}}{{\rm{P}}_3}}}$ 的值Table 1. Values of
${L_{{\rm{I}}{{\rm{P}}_3}}}$ of the key points at different$[{{\rm{IP}} _3}]$ values.$[{{\rm{IP}} _3}]$的取值/
(μmol·L–1)${\rm{SNIC}}$ ${\rm{Hopf}}$ 稳定极限环所在
区域${L_{{\rm{I}}{{\rm{P}}_3}}}$$1 $ $0.2789$ $20.8584$ $[0.2789, 20.8584]$ $1.05$ $0.2239$ $19.3199$ $[0.2239, 19.3199]$ $1.1 $ $0.1842$ $17.6358$ $[0.1842, 17.6358]$ $1.2$ $0.1317$ $13.9694$ $[0.1317, 13.9694]$ 
下载: 导出CSV
表 A1 理论模型中的参数值
Table A1. Parameter values used in the theoretical model
参数 参数值 参数 参数值 参数 参数值 ${C_{\rm{m}}}$ $ 21 \; {\rm{ {\text{μ} } F} }$ ${g_{{\rm{Na}}}}$ $28 \; {\rm{nS}}$ ${L_{{\rm{I}}{{\rm{P}}_3}}}$ ${\rm{varied, } } \;{\rm{PL} } \cdot { {\rm{s} }^{ - 1} }$ ${E_{{\rm{Na}}}}$ $50 \; {\rm{mV}}$ ${g_{\rm{K}}}$ $11.2 \; {\rm{nS}}$ ${P_{{\rm{I}}{{\rm{P}}_3}}}$ $31000 \; {\rm{PL}} \cdot {{\rm{s}}^{ - 1}}$ ${E_{\rm{K}}}$ $ - 85 \; {\rm{mV}}$ ${g_{{\rm{Nap}}}}$ $15 \; {\rm{nS}}$ ${K_{\rm{l}}}$ 1.0 μmol/L ${E_{\rm{L}}}$ $ - 58 \; {\rm{mV}}$ ${g_{ {\rm{tonic \text- e} } } }$ $0.4 \; {\rm{nS}}$ ${K_{\rm{a}}}$ 0.4 μmol/L ${E_{ {\rm{syn \text- e} } } }$ $0 \; {\rm{mV}}$ ${g_{{\rm{CAN}}}}$ $0.7 \; {\rm{nS}}$ ${V_{{\rm{SERCA}}}}$ $400 \; {\rm{aMol}} \cdot {{\rm{S}}^{ - 1}}$ ${\theta _m}$ $ - 34 \; {\rm{mV}}$ ${g_{ {\rm{syn \text- e} } } }$ $9 \; {\rm{nS}}$ ${E_{{\rm{SERCA}}}}$ 0.2 μmol/L ${\theta _n}$ $ - 29 \; {\rm{mV}}$ ${g_{\rm{L}}}$ $11.2 \; {\rm{nS}}$ $A$ $0.001 \; {({\rm{ {\text{μ} } mol} }/{\rm{L)} }^{ - 1} } \cdot {\rm{m} }{ {\rm{s} }^{ - 1} }$ ${\theta _{mp}}$ $ - 40\; {\rm{mV}}$ ${\sigma _{\rm{s}}}$ $ - 5 \; {\rm{mV}}$ ${K_{{\rm{d}}}}$ 0.4 μmol/L ${\theta _h}$ $ - 48 \; {\rm{mV}}$ ${\sigma _n}$ $ - 4 \;{\rm{mV}}$ ${K_{{\rm{CAN}}}}$ 0.74 μmol/L ${\alpha _{\rm{s}}}$ 0.2 ms-1 ${\sigma _{mp}}$ $ - 6 \; {\rm{mV}}$ ${n_{{\rm{CAN}}}}$ $0.97$ ${\bar \tau _{\rm{s}}}$ 5 ms ${\sigma _h}$ $5 \; {\rm{mV}}$ $[{\rm{I}}{{\rm{P}}_3}]$ varied, μmol/L ${\bar \tau _h}/\varepsilon $ 10000 ms ${\theta _s}$ $ - 10 \; {\rm{mV}}$ ${[{\rm{Ca}}]_{{\rm{Tot}}}}$ 1.25 μmol/L ${\bar \tau _n}$ 10 ms ${\sigma _m}$ $ - 5 \; {\rm{mV}}$ ${f_m}$ $0.000025 \; {\rm{P}}{{\rm{L}}^{ - 1}}$ $\sigma $ $0.185$
下载: 导出CSV
-
[1] Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726
Google Scholar
[2] Jens C, Rekling, Jack L, Feldman 1998 Annu. Rev. Physiol. 60 385
Google Scholar
[3] Gourévitch B, Mellen N 2014 Neuroimage 98 460
Google Scholar
[4] Lieske S P, Thoby-Brisson M, Telgkamp P, Ramirez J M 2000 Nat. Neurosci. 3 600
Google Scholar
[5] Naughton M T 2012 Thorax 67 357
Google Scholar
[6] Spiesshoefer J 2019 Int. J. Cardiol. 289 99
Google Scholar
[7] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[8] Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 382
Google Scholar
[9] Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 398
Google Scholar
[10] Kosmidis E K 2004 J. Neurophysiol. 92 686
Google Scholar
[11] Smith J C, Abdala A P L, Koizumi H, Rybak I A, Paton J F R 2007 J. Neurophysiol. 98 3370
Google Scholar
[12] Rubin J E, Hayes J A, Mendenhall J L, Del Negro C A 2009 Proc. Natl. Acad. Sci. U.S.A. 106 2939
Google Scholar
[13] Toporikova N, Butera R J 2011 J. Comput. Neurosci. 30 515
Google Scholar
[14] Park C, Rubin J E 2013 J. Comput. Neurosci. 34 345
Google Scholar
[15] Duan L X, Yuan D D, Chen X, Meng X Y 2015 Int. J. Bifurcation Chaos 25 1550069
Google Scholar
[16] 埃门创特 B 著 (吴莹, 刘深泉 译) 2010 神经科学的数学基础 (北京: 高等教育出版社) 第95−117页
Ermentrout B G, Terman D H (translated by Wu Y, Liu S Q) 2010 The Mathematical Foundations of Neuroscience (Beijing: Higher Education Press) pp95−117 (in Chinese)
[17] 尤里 · 阿 · 库兹涅佐夫 著 (金成桴 译) 2004 应用分支理论基础 (北京: 科学出版社) 第68−104页
Kuznetsov Y A (translated by Jin C F) 2004 Elements of Applied Bifurcation Theory (Beijing: Science Press) pp68−104 (in Chinese)
[18] Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171
Google Scholar
[19] Wang Y, Rubin J E 2016 J. Comput. Neurosci. 41 245
Google Scholar
[20] Lü Z S, Chen L N, Duan L X 2019 Appl. Math. Modell. 67 234
Google Scholar
[21] 王付霞, 谢勇 2013 62 020509
Google Scholar
Wang F X, Xie Y 2013 Acta Phys. Sin. 62 020509
Google Scholar
[22] Best J, Borisyuk A, Rubin J E, Terman D, Wechselberger M 2005 SIAM J. Appl. Dyn. Syst. 4 1107
Google Scholar
[23] Wang Z J, Duan L X, Cao Q Y 2018 Chin. Phys. B 27 070502
Google Scholar
[24] 杨永霞, 李玉叶, 古华光 2020 69 040501
Google Scholar
Yang Y X, Li Y Y, Gu H G 2020 Acta Phys. Sin. 69 040501
Google Scholar
[25] Morita K, Koketsu K, Kuba K 1980 Nature 283 204
Google Scholar
[26] Wang S Y, Ma X D, Yan F, Peng H X, Zheng C D, Bai C W 2004 China J. Mod. Med. 14 49
Google Scholar
[27] Goldbeter A, Dupont G 1990 Biophys. Chem. 37 341
Google Scholar
[28] Jouaville L S, lchas F, Holmnhamedov E L 1995 Nature 377 438
Google Scholar
[29] Falcke M, Hudson J L, Camacho P, Lechleiter J D 1999 Biophys. J. 77 37
Google Scholar
[30] 施小民 2003 博士学位论文 (上海: 上海大学)
Shi X M 2003 Ph. D. Dissertation (Shanghai: Shanghai University) (in Chinese)
[31] 马芬, 段利霞, 梁桐桐, 梁王娟, 赵勇 2020 动力学与控制学报 18 82
Google Scholar
Ma F, Duan L X, Liang T T, Liang W J, Zhao Y 2020 J. Dyn. Control 18 82
Google Scholar
[32] 埃门创特 B 著 (孝鹏程, 段利霞, 苏建忠 译) 2002 动力系统仿真, 分析与动画——XPPAUT使用指南 (北京: 科学出版社) 第155−167页
Ermentrout B (translated by Xiao P C, Duan L L, Su J Z) 2002 Simulating, Analyzing, and Animating Dynamical Systems : A Guide to XPPAUT for Researchers and Students (Beijing: Science Press) pp155−167 (in Chinese)
[33] Duan L X, Liu J, Chen X, Xiao P C, Zhao Y 2017 Cogn. Neurodyn. 11 91
Google Scholar
下载:
计量
- 文章访问数: 5386
- PDF下载量: 82
- 被引次数: 0
