Investigation on equation of state and ionization equilibrium for aluminum in warm dense matter regime

Wang Tian-Hao; Wang Kun; Zhang Yue; Jiang Lin-Cun

doi:10.7498/aps.69.20191826

Abstract

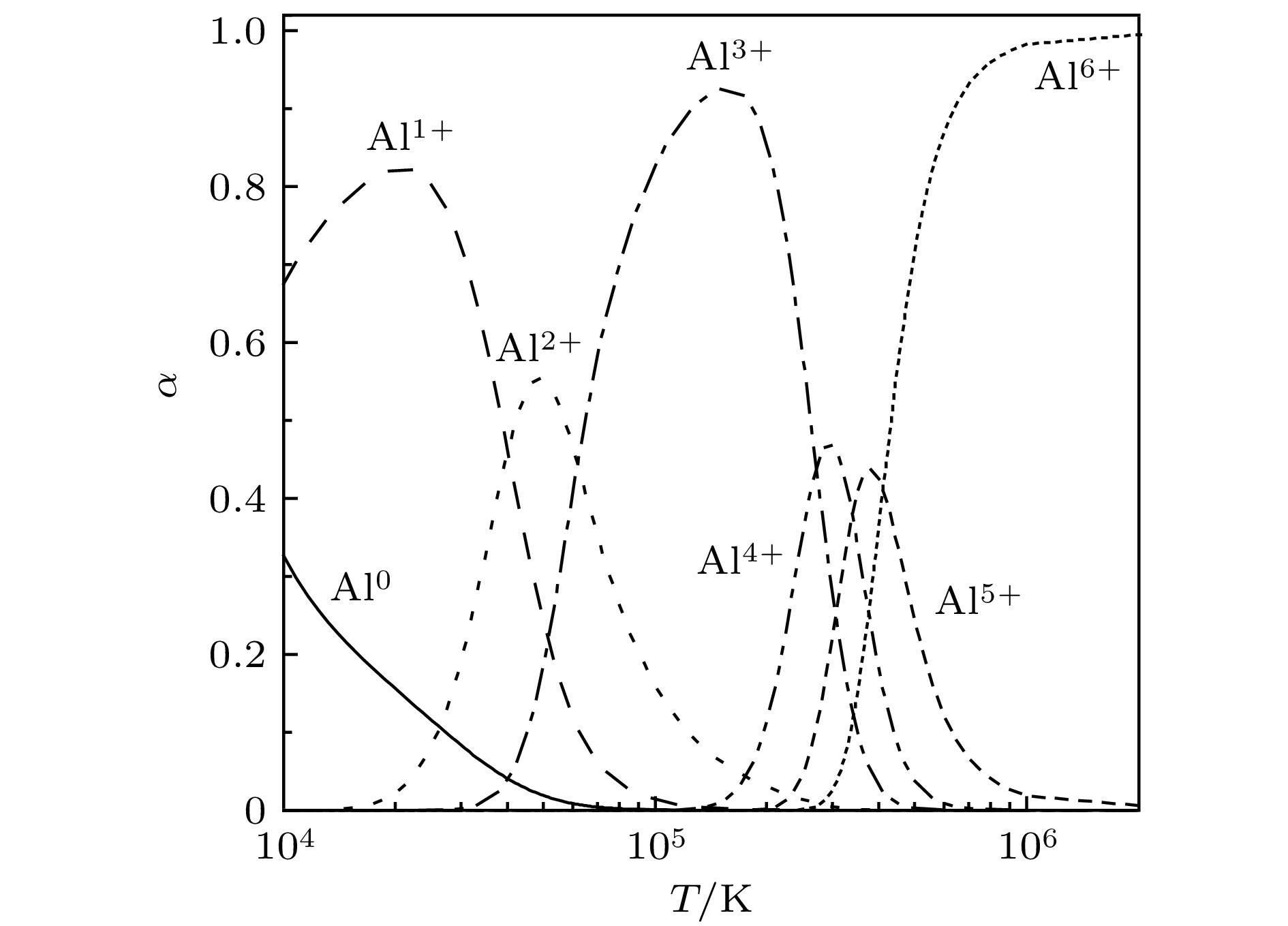
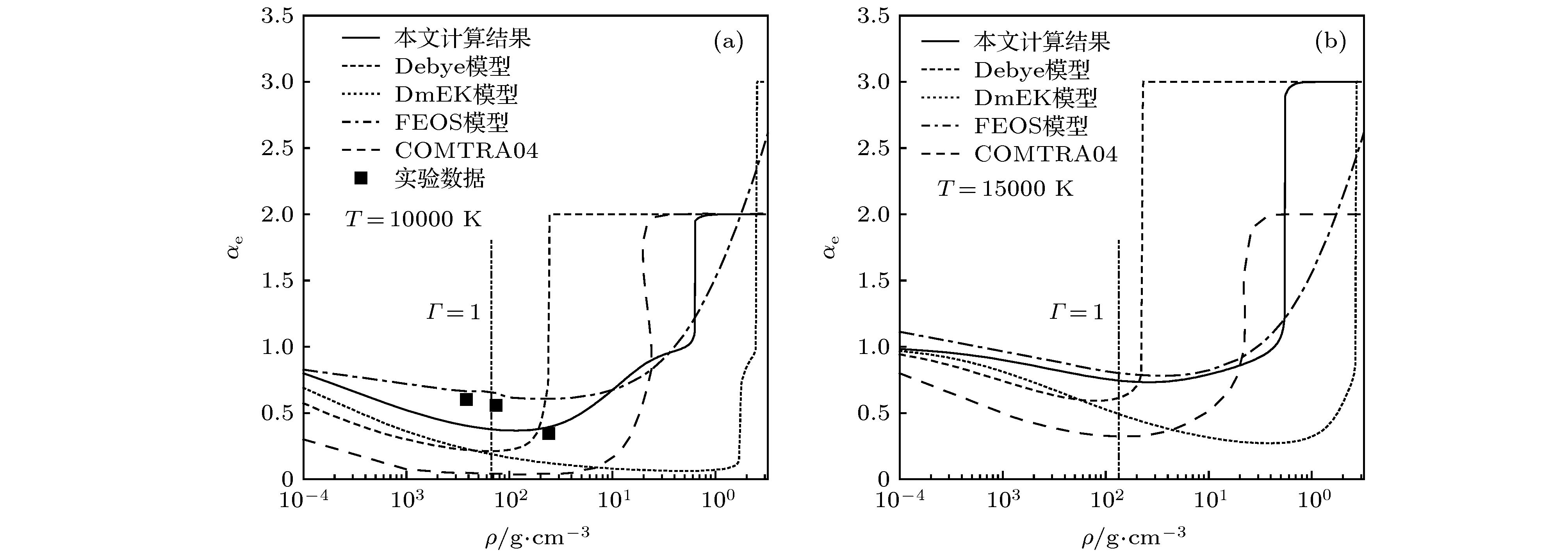
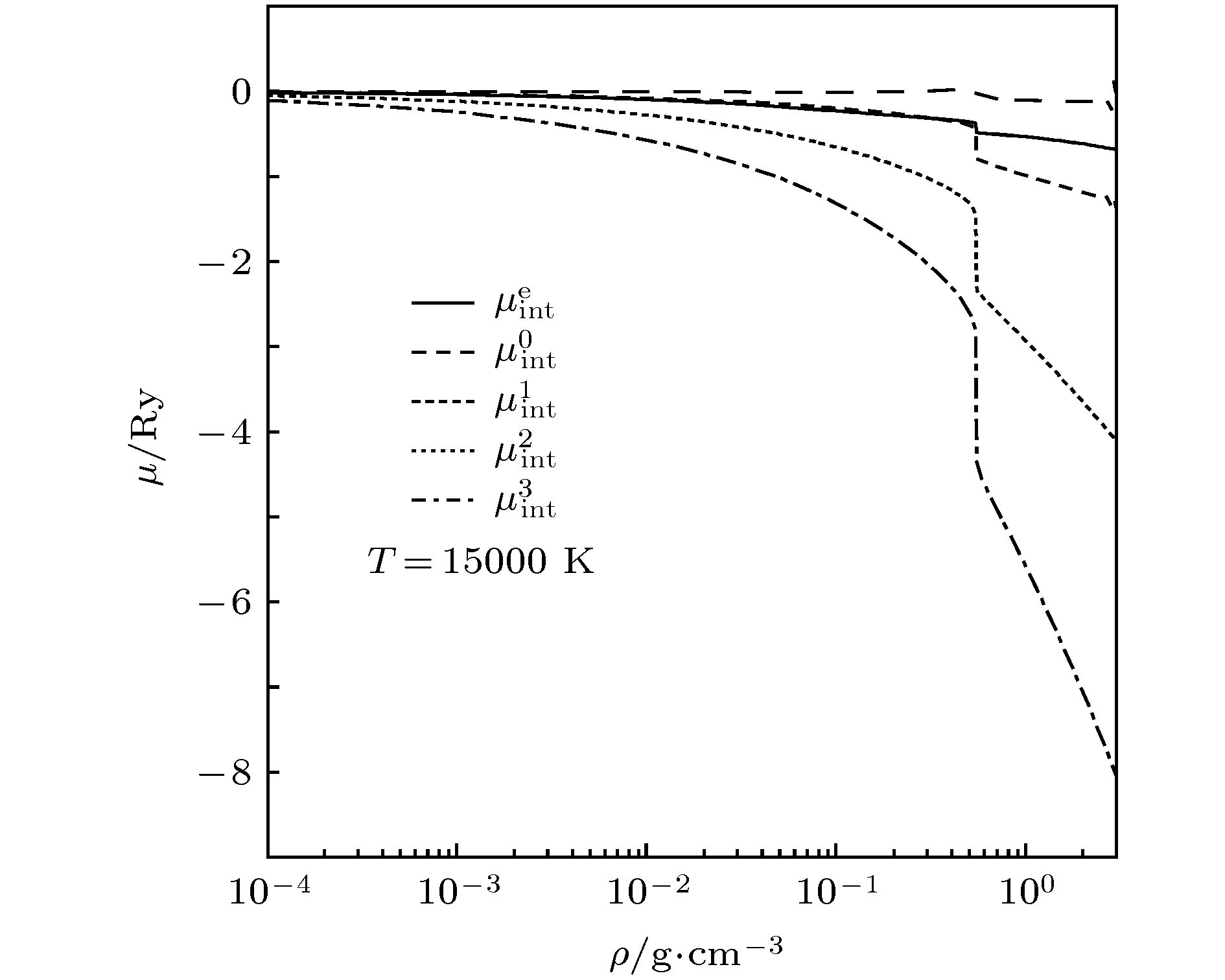
Warm dense matter is widely found in the high-energy-density-physics researches, such as inertial confinement fusion, X-ray source and wire-array Z-pinch. The equation of state and ionization equilibrium of material in warm dense matter regime play a significant role in explaining experimental results and simulations of physical process. In this paper, the Coulomb interaction between charged particles, and the excluded volume effect due to high density and polarization effect between neutral atoms and charged particles are considered in the equation of state for aluminum in warm dense matter regime. A non-ideal Saha equation is used to account for the ionization equilibrium. The data for pressure and concentration of particles of aluminum plasma are derived by iteration between equation of state and ionization equilibrium model. The pressure and average ionization degree of aluminum plasma are consistent with the calculation results from other models and relevant experimental data. The Coulomb interaction, which dominants the non-ideal effects, is insensitive to temperature and increases with density rising especially near the region of critical density. The excluded volume effect peaks at a density of ～0.5 g/cm³. The polarization effect first becomes stronger with density increasing and then decreases at a density of ～0.4 g/cm³. The ionization equilibrium results with density ranging from 1.0 × 10^–4 g/cm³ to 3.0 g/cm³ and temperature ranging from 1.0 × 10⁴ K to 3.0 × 10⁴ K reveal that the average ionization degree increases with density sharply increasing near the critical density. The non-ideal effects, which lead the ionization energy to decline and the effective ionization potential of specific ions in aluminum plasma to decrease substantially, are responsible for the sharp increase of average ionization degree near the region of critical density. When the temperature is lower than 12000 K, first and second stage of ionization occur in aluminum plasma, and the system is mainly composed of Al¹⁺, Al²⁺ and electrons. The average ionization degree can reach 2 at critical density. The third stage of ionization is dominant in the aluminum plasma when plasma temperature is higher than 12000 K. And then, the charged particles in the plasma are composed of Al³⁺ and electrons, allowing the average ionization degree to reach 3 at critical density.

Keywords:

Authors and contacts

1.
State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300130, China
2.
Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province, Hebei University of Technology, Tianjin 300130, China

Corresponding author: Wang Kun, kunwang@hebut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51807050), the Natural Science Foundation of Hebei Province, China (Grant No. E2019202297), and the Program for the Top Young and Middle-aged Innovative Talents of Higher Learning Institutions of Hebei Province, China (Grant No. BJ2017038)

FullText HTML : translate this paragraph

References

[1]	付志坚, 贾丽君, 夏继宏, 唐可, 李召红, 权伟龙, 陈其峰 2016 65 065201 Google Scholar Fu Z J, Jia L J, Xia J H, Tang K, Li Z H, Quan W L, Chen Q F 2016 Acta Phys. Sin. 65 065201 Google Scholar
[2]	Wallace M S, Haque S, Neill P, Pereira N R, Presura R 2018 Rev. Sci. Instrum. 89 015106 Google Scholar
[3]	Oreshkin V I, Artyomov A P, Chaikovsky S A, Oreshkin E V, Rousskikh A G 2017 Phys. Plasmas 24 012703 Google Scholar
[4]	格拉齐亚尼F, 德斯贾莱斯M P, 雷德默R, 特里基S B 著 (陈其峰译) 2018 温稠密物质研究的前沿和挑战 (北京: 原子能出版社) 第vii−x页 Graziani F, Desjarlais M P, Redmer R, Trickey S B (translated by Chen Q F) 2018 Frontiers and Challenges in Warm Dense Matter (Beijing: Atomic Energy Press) ppvii−x (in Chinese)
[5]	徐锡申, 张万箱 1986 实用物态方程理论导引 (北京: 科学出版社) 第1−5页 Xu X S, Zhang W X 1986 Introduction to the Theory of Equation of State (Beijing: Science Press) pp1−5 (in Chinese)
[6]	Shi Z Q, Wang K, Li Y, Shi Y J, Wu J, Jia S L 2014 Phys. Plasmas 21 032702 Google Scholar
[7]	Eliezer S, Ghatak A, Hora H, Teller E 2002 Fundamentals of Equations of State (Singapore: World Scientific) pp153−164
[8]	陈其峰, 顾云军, 郑君, 李江涛, 李治国, 权伟龙, 付志坚, 李成军 2017 科学通报 62 812 Google Scholar Chen Q F, Gu Y J, Zheng J, Li J T, Li Z G, Quan W L, Fu Z J, Li C J 2017 Chin. Sci. Bull. 62 812 Google Scholar
[9]	于继东, 李平, 王文强, 吴强 2014 63 116401 Google Scholar Yu J D, Li P, Wang W Q, Wu Q 2014 Acta Phys. Sin. 63 116401 Google Scholar
[10]	Danel J F, Kazandjian L, Zérah G 2008 Phys. Plasmas 15 072704 Google Scholar
[11]	Fu Z J, Quan W L, Zhang W, Li Z G, Zheng J, Gu Y J, Chen Q F 2017 Phys. Plasmas 24 013303 Google Scholar
[12]	汤文辉, 徐彬彬, 冉宪文, 徐志宏 2017 66 030505 Google Scholar Tang W H, Xu B B, Ran X W, Xu Z H 2017 Acta Phys. Sin. 66 030505 Google Scholar
[13]	张颖, 陈其峰, 顾云军, 蔡灵仓, 卢铁城 2007 56 1318 Google Scholar Zhang Y, Chen Q F, Gu Y J, Cai L C, Lu T C 2007 Acta Phys. Sin. 56 1318 Google Scholar
[14]	Chen Q F, Cai L C, Gu Y J, Gu Y 2009 Phys. Rev. E 79 016409 Google Scholar
[15]	Chen Q F, Zheng J, Gu Y J, Chen Y L, Cai L C 2011 Phys. Plasmas 18 112704 Google Scholar
[16]	Quan W L, Chen Q F, Fu Z J, Sun X W, Zheng J, Gu Y J 2015 Phys. Rev. E 91 023106 Google Scholar
[17]	Apfelbaum E M 2015 Phys. Plasmas 22 092703 Google Scholar
[18]	Apfelbaum E M 2017 High Temp. 55 1 Google Scholar
[19]	Kuhlbrodt S, Holst B, Redmer R 2005 Contrib. Plasma Phys. 45 73 Google Scholar
[20]	Moldabekov Z A, Groth S, Dornheim T, Bonitz M, Ramazanov T S 2017 Contrib. Plasma Phys. 57 532 Google Scholar
[21]	Stolzmann W, Blöcker T 1996 Astron. Astrophys. 314 1024
[22]	Fortov V E, Altshuler L V, Trunin R F, Funtikov A I 2004 High-Pressure Shock Compression of Solids VII (New York: Springer) pp437−489
[23]	付志坚, 陈其峰, 陈向荣 2011 60 055202 Google Scholar Fu Z J, Chen Q F, Chen X R 2011 Acta Phys. Sin. 60 055202 Google Scholar
[24]	Redmer R, Rother T, Schmidt K, Kraeft W D, Röpke G 1988 Contrib. Plasma Phys. 28 41 Google Scholar
[25]	Apfelbaum E M 2011 Phys. Rev. E 84 066403 Google Scholar
[26]	Karakhtanov V S, Redmer R, Reinholz H, Röpke G 2011 Contrib. Plasma Phys. 51 355 Google Scholar
[27]	More R M, Warren K H, Young D A, Zimmerman G B 1988 Phys. Fluids 31 3059 Google Scholar
[28]	Iyetomi H, Ichimaru S 1986 Phys. Rev. A 34 433 Google Scholar
[29]	Kresse G, Hafner J 1993 Phys. Rev. B 47 558 Google Scholar
[30]	Zaghloul M R 2018 High Energy Density Phys. 26 8 Google Scholar
[31]	Wu B, Shin Y C 2006 Appl. Phys. Lett. 89 111902 Google Scholar
[32]	Morel V, Bultel A, Chéron B G 2009 Int. J. Thermophys. 30 1853 Google Scholar
[33]	Preston T R, Vinko S M, Ciricosta O, Chung H K, Lee R W, Wark J S 2013 High Energy Density Phys. 9 258 Google Scholar
[34]	Stransky M 2016 Phys. Plasmas 23 012708 Google Scholar
[35]	Kemp A J, Meyer-Ter-Vehn J 1998 Nucl. Instrum. Methods Phys. Res., Sect. A 415 674 Google Scholar
[36]	Krisch I, Kunze H J 1998 Phys. Rev. E 58 6557 Google Scholar
[37]	田庆云 2015 硕士学位论文 (长沙: 国防科学技术大学) Tian Q Y 2015 M. S. Thesis (Changsha: National University of Defense Technology) (in Chinese)
[38]	Son S K, Thiele R, Jurek Z, Ziaja B, Santra R 2014 Phys. Rev. X 4 031004
[39]	Ebeling W, Föster A, Fortov V E, Gryaznov V K, Polishuk A Y 1991 Thermophysical Properties of Hot Dense Plasmas (Stuttgar-Leipzig: Teubner Verlagsgesellshaft) pp39—42

Cited By

图 1 在密度为0.1 g/cm³时, 不同模型计算的铝等离子体压强随温度的变化

Figure 1. The pressure of aluminum plasma calculated by different models as a function of temperature at density of 0.1 g/cm³.

DownLoad: Full-Size Img PowerPoint

图 2 铝等离子体的平均电离度随密度与温度变化等值线分布

Figure 2. Contour map of average ionization degree of aluminum plasma as a function of density and temperature.

DownLoad: Full-Size Img PowerPoint

图 3 等离子体中不同粒子的相对粒子分数在密度为0.1 g/cm³时随温度的变化

Figure 3. Dependence of relative particle fraction of different particles on temperature at density of 0.1 g/cm³.

DownLoad: Full-Size Img PowerPoint

图 4 不同模型计算的铝等离子体平均电离度在不同温度下随密度的变化　(a) 10000 K; (b) 15000 K

Figure 4. Average ionization degree of aluminum plasma calculated by different models as a function of density at different temperatures: (a) 10000 K; (b) 15000 K.

DownLoad: Full-Size Img PowerPoint

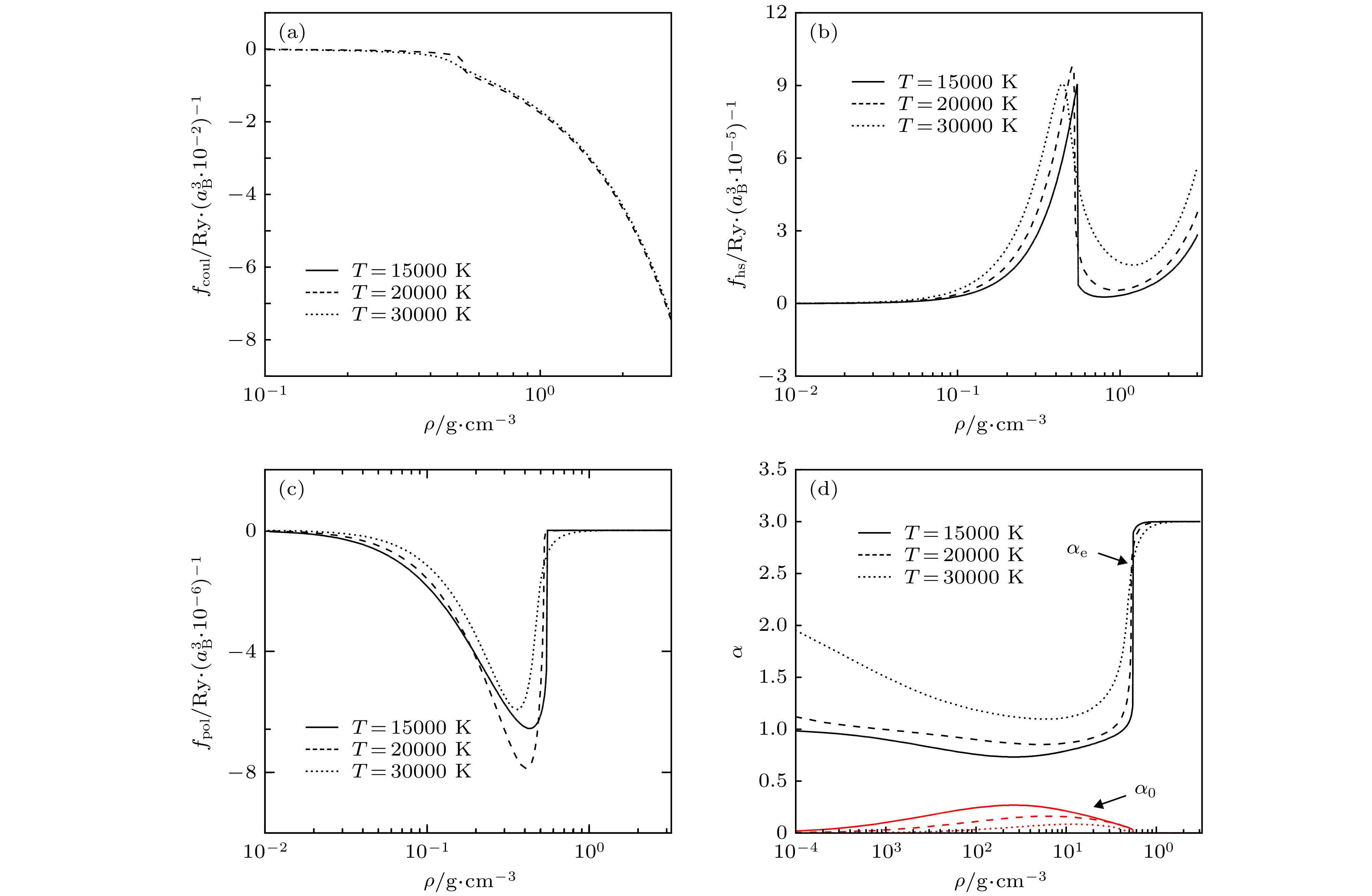
图 5 不同温度下非理想效应自由能密度以及电子、原子相对粒子分数随密度的变化　(a) 库仑相互作用; (b) 排斥体积作用; (c) 极化作用; (d) 电子、原子相对粒子分数

Figure 5. Free energy density of different non-ideal effects and relative particle fraction for electrons and atoms as a function of density at different temperatures: (a) Coulomb interaction; (b) excluded volume effect; (c) polarization effect; (d) relative particle fraction for electrons and atoms.

DownLoad: Full-Size Img PowerPoint

图 6 温度为15000 K时等离子体中不同粒子化学势的非理想部分随密度的变化

Figure 6. Dependence of non-ideal chemical potential of particles on density at temperature of 15000 K.

DownLoad: Full-Size Img PowerPoint

图 7 温度为15000 K时不同模型计算的电离能的降低∆E随密度的变化(黑色曲线, 非理想Saha方程; 红色曲线, DmEK模型)

Figure 7. Depression of ionization potential calculated by different models as a function of density at 15000 K. Black lines correspond to nonideal Saha equation; red lines correspond to DmEK model.

DownLoad: Full-Size Img PowerPoint

表 1 物态方程及电离平衡模型参数列表

Table 1. Parameters of equation of state and ionization equilibrium model.

参数值参数值参数值

R₀ 2.5714 R₆ 0.4167 E₃ 2.0909
R₁ 2.3377 r_c 1.7712 E₄ 8.8192
R₂ 2.1429 m_k 24597 E₅ 11.3059
R₃ 0.4678 α_D 46.281 E₆ 14.0008
R₄ 0.4494 E₁ 0.4400
R₅ 0.4324 E₂ 1.3839

DownLoad: CSV

map

[1]	付志坚, 贾丽君, 夏继宏, 唐可, 李召红, 权伟龙, 陈其峰 2016 65 065201 Google Scholar Fu Z J, Jia L J, Xia J H, Tang K, Li Z H, Quan W L, Chen Q F 2016 Acta Phys. Sin. 65 065201 Google Scholar
[2]	Wallace M S, Haque S, Neill P, Pereira N R, Presura R 2018 Rev. Sci. Instrum. 89 015106 Google Scholar
[3]	Oreshkin V I, Artyomov A P, Chaikovsky S A, Oreshkin E V, Rousskikh A G 2017 Phys. Plasmas 24 012703 Google Scholar
[4]	格拉齐亚尼F, 德斯贾莱斯M P, 雷德默R, 特里基S B 著 (陈其峰译) 2018 温稠密物质研究的前沿和挑战 (北京: 原子能出版社) 第vii−x页 Graziani F, Desjarlais M P, Redmer R, Trickey S B (translated by Chen Q F) 2018 Frontiers and Challenges in Warm Dense Matter (Beijing: Atomic Energy Press) ppvii−x (in Chinese)
[5]	徐锡申, 张万箱 1986 实用物态方程理论导引 (北京: 科学出版社) 第1−5页 Xu X S, Zhang W X 1986 Introduction to the Theory of Equation of State (Beijing: Science Press) pp1−5 (in Chinese)
[6]	Shi Z Q, Wang K, Li Y, Shi Y J, Wu J, Jia S L 2014 Phys. Plasmas 21 032702 Google Scholar
[7]	Eliezer S, Ghatak A, Hora H, Teller E 2002 Fundamentals of Equations of State (Singapore: World Scientific) pp153−164
[8]	陈其峰, 顾云军, 郑君, 李江涛, 李治国, 权伟龙, 付志坚, 李成军 2017 科学通报 62 812 Google Scholar Chen Q F, Gu Y J, Zheng J, Li J T, Li Z G, Quan W L, Fu Z J, Li C J 2017 Chin. Sci. Bull. 62 812 Google Scholar
[9]	于继东, 李平, 王文强, 吴强 2014 63 116401 Google Scholar Yu J D, Li P, Wang W Q, Wu Q 2014 Acta Phys. Sin. 63 116401 Google Scholar
[10]	Danel J F, Kazandjian L, Zérah G 2008 Phys. Plasmas 15 072704 Google Scholar
[11]	Fu Z J, Quan W L, Zhang W, Li Z G, Zheng J, Gu Y J, Chen Q F 2017 Phys. Plasmas 24 013303 Google Scholar
[12]	汤文辉, 徐彬彬, 冉宪文, 徐志宏 2017 66 030505 Google Scholar Tang W H, Xu B B, Ran X W, Xu Z H 2017 Acta Phys. Sin. 66 030505 Google Scholar
[13]	张颖, 陈其峰, 顾云军, 蔡灵仓, 卢铁城 2007 56 1318 Google Scholar Zhang Y, Chen Q F, Gu Y J, Cai L C, Lu T C 2007 Acta Phys. Sin. 56 1318 Google Scholar
[14]	Chen Q F, Cai L C, Gu Y J, Gu Y 2009 Phys. Rev. E 79 016409 Google Scholar
[15]	Chen Q F, Zheng J, Gu Y J, Chen Y L, Cai L C 2011 Phys. Plasmas 18 112704 Google Scholar
[16]	Quan W L, Chen Q F, Fu Z J, Sun X W, Zheng J, Gu Y J 2015 Phys. Rev. E 91 023106 Google Scholar
[17]	Apfelbaum E M 2015 Phys. Plasmas 22 092703 Google Scholar
[18]	Apfelbaum E M 2017 High Temp. 55 1 Google Scholar
[19]	Kuhlbrodt S, Holst B, Redmer R 2005 Contrib. Plasma Phys. 45 73 Google Scholar
[20]	Moldabekov Z A, Groth S, Dornheim T, Bonitz M, Ramazanov T S 2017 Contrib. Plasma Phys. 57 532 Google Scholar
[21]	Stolzmann W, Blöcker T 1996 Astron. Astrophys. 314 1024
[22]	Fortov V E, Altshuler L V, Trunin R F, Funtikov A I 2004 High-Pressure Shock Compression of Solids VII (New York: Springer) pp437−489
[23]	付志坚, 陈其峰, 陈向荣 2011 60 055202 Google Scholar Fu Z J, Chen Q F, Chen X R 2011 Acta Phys. Sin. 60 055202 Google Scholar
[24]	Redmer R, Rother T, Schmidt K, Kraeft W D, Röpke G 1988 Contrib. Plasma Phys. 28 41 Google Scholar
[25]	Apfelbaum E M 2011 Phys. Rev. E 84 066403 Google Scholar
[26]	Karakhtanov V S, Redmer R, Reinholz H, Röpke G 2011 Contrib. Plasma Phys. 51 355 Google Scholar
[27]	More R M, Warren K H, Young D A, Zimmerman G B 1988 Phys. Fluids 31 3059 Google Scholar
[28]	Iyetomi H, Ichimaru S 1986 Phys. Rev. A 34 433 Google Scholar
[29]	Kresse G, Hafner J 1993 Phys. Rev. B 47 558 Google Scholar
[30]	Zaghloul M R 2018 High Energy Density Phys. 26 8 Google Scholar
[31]	Wu B, Shin Y C 2006 Appl. Phys. Lett. 89 111902 Google Scholar
[32]	Morel V, Bultel A, Chéron B G 2009 Int. J. Thermophys. 30 1853 Google Scholar
[33]	Preston T R, Vinko S M, Ciricosta O, Chung H K, Lee R W, Wark J S 2013 High Energy Density Phys. 9 258 Google Scholar
[34]	Stransky M 2016 Phys. Plasmas 23 012708 Google Scholar
[35]	Kemp A J, Meyer-Ter-Vehn J 1998 Nucl. Instrum. Methods Phys. Res., Sect. A 415 674 Google Scholar
[36]	Krisch I, Kunze H J 1998 Phys. Rev. E 58 6557 Google Scholar
[37]	田庆云 2015 硕士学位论文 (长沙: 国防科学技术大学) Tian Q Y 2015 M. S. Thesis (Changsha: National University of Defense Technology) (in Chinese)
[38]	Son S K, Thiele R, Jurek Z, Ziaja B, Santra R 2014 Phys. Rev. X 4 031004
[39]	Ebeling W, Föster A, Fortov V E, Gryaznov V K, Polishuk A Y 1991 Thermophysical Properties of Hot Dense Plasmas (Stuttgar-Leipzig: Teubner Verlagsgesellshaft) pp39—42

[1]	Zhang Zhi-Yu, Zhao Yang, Qing Bo, Zhang Ji-Yan, Lin Cheng-Liang, Yang Guo-Hong, Wei Min-Xi, Xiong Gang, Lü Min, Huang Cheng-Wu, Zhu Tuo, Song Tian-Ming, Zhao Yan, Zhang Yu-Xue, Zhang Lu, Li Li-Ling, Du Hua-Bing, Che Xing-Sen, Li Yu-Kun, Zhan Xia-Yu, Yang Jia-Min. Experimental method for warm dense matter ionization distribution based on X-ray fluorescence pectroscopy. Acta Physica Sinica, 2024, 73(1): 015201. doi: 10.7498/aps.73.20231216
[2]	Zhang Zhi-Yu, Zhao Yang, Qing Bo, Zhang Ji-Yan, Lin Cheng-Liang, Yang Guo-Hong, Wei Min-Xi, Xiong Gang, Lv Min, Huang Cheng-Wu, Zhu Tuo, Song Tian-Ming, Zhao Yan, Zhang Yu-Xue, Zhang Lu, Li Li-Ling, Du Hua-Bing, Che Xing-Sen, Li Yu-Kun, Zan Xia-Yu, Yang Jia-Min. Study of experimental method for warm dense matter ionization distribution based on x-ray fluorescence spectroscopy. Acta Physica Sinica, 2023, 0(0): 0-0. doi: 10.7498/aps.72.20231216
[3]	Zhang Zhi-Yu, Zhao Yang, Qing Bo, Zhang Ji-Yan, Ma Jian-Yi, Lin Cheng-Liang, Yang Guo-Hong, Wei Min-Xi, Xiong Gang, Lü Min, Huang Cheng-Wu, Zhu Tuo, Song Tian-Ming, Zhao Yan, Zhang Yu-Xue, Zhang Lu, Li Li-Ling, Du Hua-Bing, Che Xing-Sen, Li Yu-Kun, Zhan Xia-Yu, Yang Jia-Min. Density effect on electronic structure of warm dense matter based on X-ray fluorescence spectroscopy. Acta Physica Sinica, 2023, 72(24): 245201. doi: 10.7498/aps.72.20231215
[4]	Tian Chun-Ling, Liu Hai-Yan, Wang Biao, Liu Fu-Sheng, Gan Yun-Dan. Phase transition and equation of state of dense liquid nitrogen at high temperature and high pressure. Acta Physica Sinica, 2022, 71(15): 158701. doi: 10.7498/aps.71.20220124
[5]	Jin Yang, Zhang Ping, Li Yong-Jun, Hou Yong, Zeng Jiao-Long, Yuan Jian-Min. Influence of different charge-state ion distribution on elastic X-ray scattering in warm dense matter. Acta Physica Sinica, 2021, 70(7): 073102. doi: 10.7498/aps.70.20201483
[6]	Jin Kang, Jing Guang-Yin. Pressure of active system under the electric double layer interaction. Acta Physica Sinica, 2019, 68(17): 170501. doi: 10.7498/aps.68.20190435
[7]	Ma Gui-Cun, Zhang Qi-Li, Song Hong-Zhou, Li Qiong, Zhu Xi-Rui, Meng Xu-Jun. Theoretical study of the equation of state for warm dense matter. Acta Physica Sinica, 2017, 66(3): 036401. doi: 10.7498/aps.66.036401
[8]	Wu Na, Yang Jiao, Xiao Fen, Cai Ling-Cang, Tian Chun-Ling. Equation of state of solid krypton from correlated quantum chemistry calculations. Acta Physica Sinica, 2014, 63(14): 146102. doi: 10.7498/aps.63.146102
[9]	Peng Xiao-Juan, Liu Fu-Sheng. Problem and modification to the equation of state for liquid and solid-liquid mixed phase in Grover model. Acta Physica Sinica, 2012, 61(18): 186201. doi: 10.7498/aps.61.186201
[10]	Zheng Jun, Gu Yun-Jun, Chen Qi-Feng, Chen Zhi-Yun. Compression properties of rare gases in region of ionization. Acta Physica Sinica, 2010, 59(10): 7472-7477. doi: 10.7498/aps.59.7472
[11]	Gu Yun-Jun, Zheng Jun, Chen Zhi-Yun, Chen Qi-Feng, Cai Ling-Cang. The equation of state of H2+He fluid mixture in the region of partial dissociation. Acta Physica Sinica, 2010, 59(7): 4508-4513. doi: 10.7498/aps.59.4508
[12]	Zhao Yan-Hong, Liu Hai-Feng, Zhang Gong-Mu. Equation of state of detonation products based on statistical mechanical theory. Acta Physica Sinica, 2007, 56(8): 4791-4797. doi: 10.7498/aps.56.4791
[13]	Tian Chun-Ling, Cai Ling-Cang, Gu Yun-Jun, Jing Fu-Qian, Chen Zhi-Yun. Investigation of the pressure-volume-temperature equation of state for dense hydrogen-helium mixture using multi-shock compression method. Acta Physica Sinica, 2007, 56(7): 4180-4186. doi: 10.7498/aps.56.4180
[14]	Hou Yong, Yuan Jian-Min. First-principle calculations of phase transitions and equation of state at T=0K for gold. Acta Physica Sinica, 2007, 56(6): 3458-3463. doi: 10.7498/aps.56.3458
[15]	Tian Yang-Meng, Wang Cai-Xia, Jiang Ming, Cheng Xin-Lu, Yang Xiang-Dong. State equation of inert plasma. Acta Physica Sinica, 2007, 56(10): 5698-5703. doi: 10.7498/aps.56.5698
[16]	Zhang Ying, Chen Qi-Feng, Gu Yun-Jun, Cai Ling-Cang, Lu Tie-Cheng. Self-consistent variational calculation of the dense fluid helium plasma in the region of partial ionization. Acta Physica Sinica, 2007, 56(3): 1318-1324. doi: 10.7498/aps.56.1318
[17]	Wang Cai-Xia, Tian Yang-Meng, Jiang Ming, Cheng Xin-Lu, Yang Xiang-Dong, Meng Chuan-Min. A simplified model for computing state equation of argon plasma. Acta Physica Sinica, 2006, 55(11): 5784-5789. doi: 10.7498/aps.55.5784
[18]	Li Xiao-Jie. . Acta Physica Sinica, 2002, 51(5): 1098-1102. doi: 10.7498/aps.51.1098
[19]	GENG HUA-YUN, WU QIANG, TAN HUA. STATISTICAL PARAMETER OF THERMODYNAMIC EQUATION OF STATE. Acta Physica Sinica, 2001, 50(7): 1334-1339. doi: 10.7498/aps.50.1334
[20]	HUA JING-SONG, JIN FU-QIAN, TAN HUA. A THEORETICAL METHOD TO OBTAIN THE SECOND ORDER PARTIAL DERIVATIVE OF SHEAR MODU LUS WITH RESPECT TO PRESSURE. Acta Physica Sinica, 2000, 49(12): 2443-2447. doi: 10.7498/aps.49.2443

Catalog

Vol. 69, Issue 9 - 2020-05-05

Metrics

Abstract views: 7511
PDF Downloads: 114
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板