-
Based on the existing experimental data of nuclear radius, the previous formula of nuclear charge radius is verified and discussed. Comparing the formula of the single-parameter nuclear charge radius, it is proved that the formula of
$Z^{1/3}$ law is better than the formula of$A^{1/3}$ law. We refitted the two-parameter formula and the three-parameter formula that have been proposed and confirmed that the two-parameter and three-parameter formula fit better than the single-parameter formula. It is shown that show that the deformation plays a key role in the nuclear charge radius. The electric quadrupole moment is an important physical quantity representing the properties of the nucleus. Its appearance indicates the deviation from spherical symmetry and also reflects the size of the nuclear deformation. The electric quadrupole moment is also one of the basic observations to understand the distribution of matter within the nucleus, to examine the nuclear model, and to observe nucleon-nuclear interactions. Taking into account the relationship between the nuclear quadrupole moment and the deformation, the electric quadrupole moment factor is added to the original three-parameter formula to obtain a new formula for the nuclear charge radius. Fitting the four-parameter formula, it is found that the theoretical value of the nuclear charge radius is in good agreement with the experimental value, the root-mean-square deviation is 0.0397 fm. Considering the relationship between the total spin and the electric quadrupole moment, the intrinsic electric quadrupole moment is obtained and brought into the formula for fitting, and the root-mean-square deviation further decreases,the root-mean-square deviation is 0.0372 fm. Finally, considering the universality of odd-even staggering, we add the$\delta$ term that can reflect the odd and even oscillation phenomenon, and the root-mean-square deviation obtained by the formula is 0.369 fm, which better reflects the relationship between the deformation and the nuclear charge radius. Compared with the formulas already proposed, the new formula can better reflect the variation trend of nuclear deformation, shell effect, odd-even staggering, etc., and the calculation accuracy is also improved, which can provide a useful reference for future experiments.-
Keywords:
- nuclear charge radius /
- quadrupole moment /
- spin
[1] De Vries H, De Jager C W, De Vries C 1987 At. Data Nucl. Data Tables 36 495
Google Scholar
[2] Boehm E, Lee P L 1974 At. Data Nucl. Data Tables 14 605
Google Scholar
[3] Engfer R, Schneuwly H, Vuileumier J L, Walter H K, Zehnder A 1974 At. Data Nucl. Data Tables 14 509
Google Scholar
[4] Fricke G, Bernhardt C, Heilig K, Schaller L A, Schellenberg L, Shera E B, De Jager C W 1995 At. Data Nucl. Data Tables 60 177
Google Scholar
[5] Heilig K, Steudel A 1974 At. Data Nucl. Data Tables 14 613
Google Scholar
[6] Aufmuth P, Heilig K, Steudel A 1987 At. Data Nucl. Data Tables 37 455
Google Scholar
[7] Angeli I, Marinova K P 2013 At. Data Nucl. Data Tables 99 69
Google Scholar
[8] Nerlo-Pomorska B, Pomorski K 1993 Z. Phys. A 344 359
Google Scholar
[9] Nerlo-Pomorska B, Pomorski K 1994 Z. Phys. A 348 169
Google Scholar
[10] 圣宗强, 樊广伟, 钱建发 2015 64 112101
Google Scholar
Sheng Z Q, Fan G W, Qian J F 2015 Acta Phys. sin. 64 112101
Google Scholar
[11] 曾谨言 1957 13 357
Google Scholar
Zeng J Y 1957 Acta Phys. Sin. 13 357
Google Scholar
[12] 曾谨言 1975 24 151
Google Scholar
Zeng J Y 1975 Acta Phys. Sin. 24 151
Google Scholar
[13] 张双全, 孟杰, 周善贵, 曾谨言 2002 高能物理与核物理 26 252
Google Scholar
Zhang S Q, Meng J, Zhou S G, Zeng J Y 2002 High Energy Physics and Nuclear Physics 26 252
Google Scholar
[14] Barzakh A E, Fedorov D V, Ivanov V S, Molkanov P L, Moroz F V, Orlov S Y, Panteleev V N, Seliverstov M D, Volkov M Y 2018 Phys. Rev. C 97 014322
Google Scholar
[15] Yang J J, Piekarewicz J 2018 Phys. Rev. C 97 014314
Google Scholar
[16] Safronova M S, Porsev S G, Kozlov M G, Thielking J, Okhapkin M V, Glowacki P, Meier D M, Peik E 2018 Phys. Rev. Lett. 121 213001
Google Scholar
[17] Casten R F 1985 Phys. Rev. Lett. 54 1991
Google Scholar
[18] Casten R F, Brenner D S, Haustein P E 1987 Phys. Rev. Lett. 58 658
Google Scholar
[19] Casten R F 1988 J. Phys. G: Nucl. Part. Phys. 14 S71
Google Scholar
[20] Casten R F, Zamfir N V 1993 Phys. Rev. Lett. 70 402
Google Scholar
[21] Foy B D, Casten R F, Zamfir N V, Brenner D S 1994 Phys. Rev. C 49 1224
[22] Saha M, Sen S 1994 Phys. Rev. C 49 2460
[23] Gangopadhyar G 2009 J. Phys. G: Nucl. Part. Phys. 36 095105
Google Scholar
[24] Stopkowicz S, Gauss J 2014 Phys. Rev. A 90 022507
Google Scholar
[25] Zhao P W, Zhang S Q, Meng J 2014 Phys. Rev. C 89 011301
Google Scholar
[26] Otsuka T, Suzuki T, Fujimoto R, Grawe H, Akaish Y 2005 Phys. Rev. Lett. 95 232502
Google Scholar
[27] Bohr A 1976 Science 48 365
[28] Cheal B, Mane E, Billowes J, Bissell M L, Blaum K, Brown B A, Charlwood F C, Flanagan K T, Forest D H, Geppert C, Honma M, Jokinen A, Kowalska M, Krieger A, Kramer J, Moore I D, Neugart R, Neyens G, Nortershauser W, Schug M, Stroke H H, Vingerhoets P, Yordanov D T, Zakova M 2010 Phys. Rev. Lett. 104 202502
[29] Ohtsubo T, Stone N J, Stone J R, Towner I S, Bingham C R, Gaulard C, Koster U, Muto S, Nikolov J, Nishimura K, Simpson G S, Soti G, Veskovic M, Walters W B, Wauters F 2012 Phys. Rev. Lett. 109 032504
Google Scholar
[30] Snyder J B, Reviol W, Sarantites D G, Afanasjev A V, Janssens R V F, Abusara H, Carpenter M P, Chen X, Chiara C J, Greene J P, Lauritsen T, McCutchan E A, Seweryniak D, Zhu S 2013 Phys. Rev. B 723 61
[31] Heyde K, Wood J L 2011 Rev. Mod. Phys. 83 1467
Google Scholar
[32] Yordanov D T, Balabanski D L, Bieron J, Bissell M L, Blaum K, Budincevic I, Frizsche S, Frommgen N, Georgiev G 2013 Phys. Rev. Lett. 110 192501
Google Scholar
[33] 陈春杏 2015 硕士学位论文 (广西: 广西师范大学)
Chen C X 2015 M. S. Thesis (Guangxi: Guangxi Normal University) (in Chinese)
[34] Stone N J 2016 At. Data Nucl. Data Tables 111-112 1
Google Scholar
-
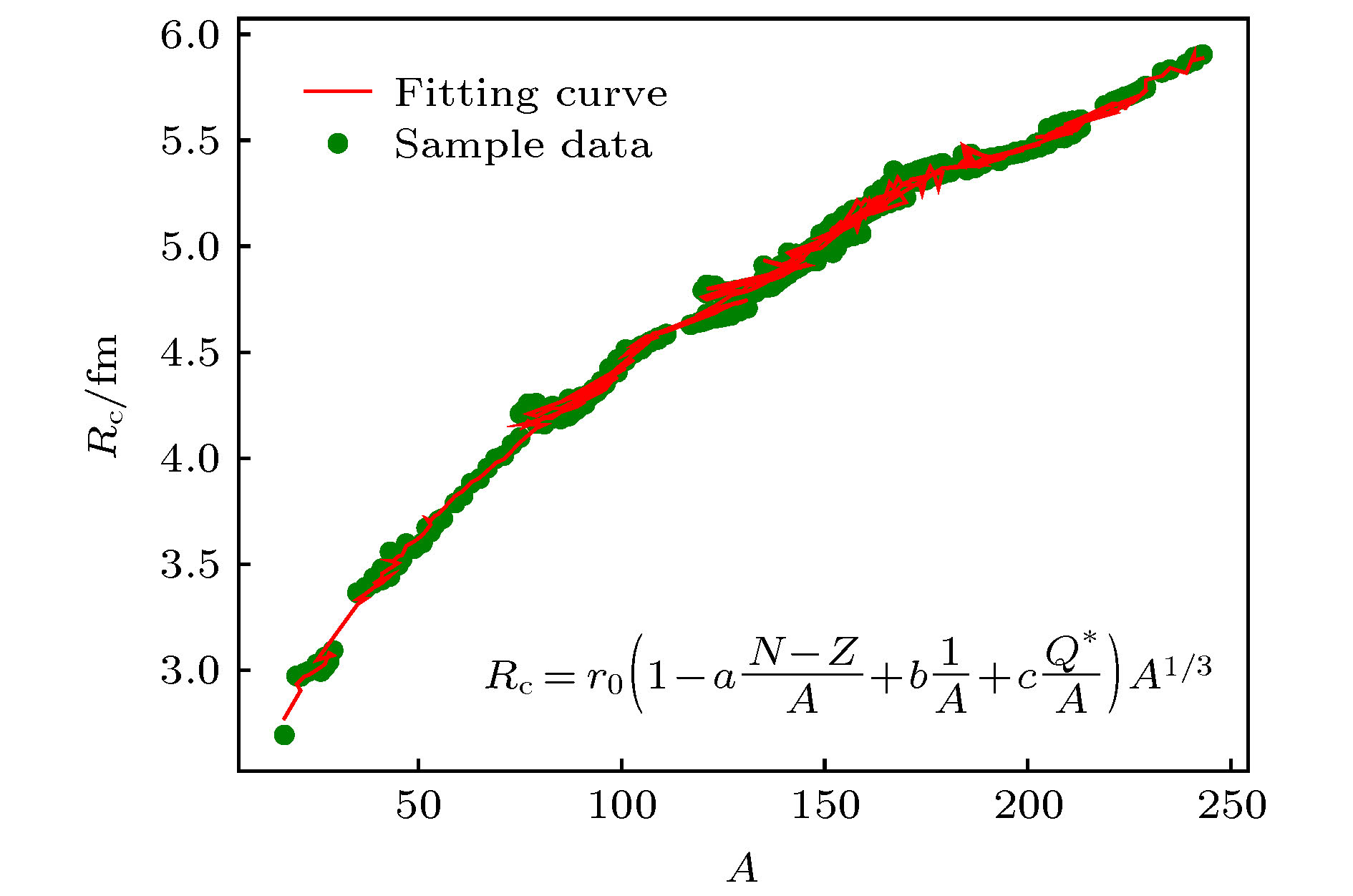
图 1
$ R_{\rm c} = r_0 A^{1/3} $ 与$ R_{\rm c} = r_0 Z^{1/3} $ 的拟合曲线(左图是$ R_{\rm c} = r_0 A^{1/3} $ 的拟合曲线, 右图是$ R_{\rm c} = r_0 Z^{1/3} $ 的拟合曲线)Figure 1. The fitting curve of the Eqs. (2) and (4).(The left picture is the fitting curve of the Eq. (2) and the right picture is the fitting curve of the Eq. (4))
图 2
$R_{\rm c}=r_0\left( 1-a\dfrac{N-Z}{A}+b\dfrac{1}{A}+c\dfrac{Q^*}{A} \right)A^{1/3}$ 的拟合曲线图Figure 2. The fitting curve of the Eq. (13).
图 3
$R_{\rm c}=r_0\left( 1-a\dfrac{N-Z}{A}+b\dfrac{1}{A}+c\dfrac{Q_0^*}{A} \right)A^{1/3}$ 的拟合曲线图Figure 3. The fitting curve of the Eq. (14).
图 4
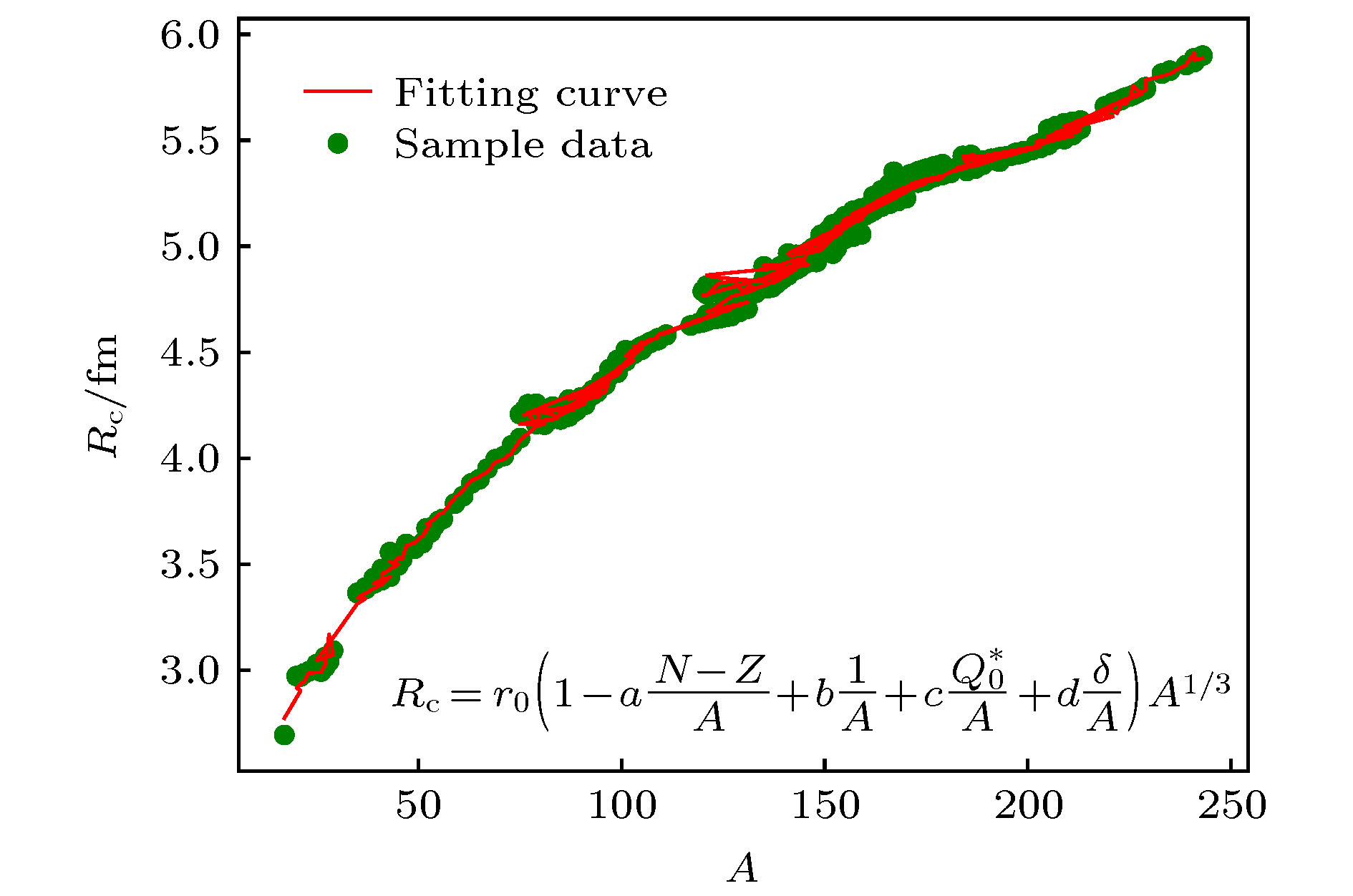
$R_{\rm c}=r_0\left( 1-a\dfrac{N-Z}{A}+b\dfrac{1}{A}+c\dfrac{Q_0^*}{A}+d\frac{\delta}{A} \right)A^{1/3}$ 的拟合曲线图Figure 4. The fitting curve of the Eq. (15).
表 1 各种核电荷半径公式
Table 1. The mentioned equations for nuclear charge radius
$R_{\rm c}$ .公式 参数 σ/fm ${R_{\rm c}} = {r_0}A^{1/3}$ r0 = 1.2269 fm σ = 0.1224 ${R_{\rm c}} = {r_0}Z^{1/3}$ r0 = 1.6394 fm σ = 0.0939 ${R_{\rm c}} = {r_0}\left( {1 - a\dfrac{ {N - Z} }{A} } \right){A^{1/3} }$ r0 = 1.2827 fm, a = 0.2700 σ = 0.0855 ${R_{\rm c}} = {r_0}\left( {1 - a\dfrac{ {N - Z} }{A} + b\dfrac{1}{A} } \right){A^{1/3} }$ r0 = 1.2331 fm, a = 0.1461, b = 2.3301 σ = 0.0510 ${R_{\rm c}} = {r_0}\left( {1 + a\dfrac{ {N - {N^*} } }{Z} } \right){Z^{1/3} }$ r0 = 1.6312 fm, a = 0.0627 σ = 0.0618 ${R_{\rm c}} = {r_0}\left( {1 - a\dfrac{ {N - Z} }{A} + b\dfrac{1}{A} + c\dfrac{ { {Q^*} } }{A} } \right){A^{1/3} }$ r0 = 1.2221 fm, a = 0.1350, b = 2.4698, c = 0.8976 σ = 0.0397 ${R_{\rm c}} = {r_0}\left( {1 - a\dfrac{ {N - Z} }{A} + b\dfrac{1}{A} + c\dfrac{ {Q_0^*} }{A} } \right){A^{1/3} }$ r0 = 1.2220 fm, a = 0.1410, b = 2.4200, c = 0.3643 σ = 0.0372 ${R_{\rm c}} = {r_0}\left( {1 - a\dfrac{ {N - Z} }{A} + b\dfrac{1}{A} + c\dfrac{ {Q_0^*} }{A} + d\dfrac{\delta }{A} } \right){A^{1/3} }$ r0 = 1.2223 fm, a = 0.1421, b = 2.4577,
c = 0.3660 d = 0.1705σ = 0.0369 
DownLoad: CSV
-
[1] De Vries H, De Jager C W, De Vries C 1987 At. Data Nucl. Data Tables 36 495
Google Scholar
[2] Boehm E, Lee P L 1974 At. Data Nucl. Data Tables 14 605
Google Scholar
[3] Engfer R, Schneuwly H, Vuileumier J L, Walter H K, Zehnder A 1974 At. Data Nucl. Data Tables 14 509
Google Scholar
[4] Fricke G, Bernhardt C, Heilig K, Schaller L A, Schellenberg L, Shera E B, De Jager C W 1995 At. Data Nucl. Data Tables 60 177
Google Scholar
[5] Heilig K, Steudel A 1974 At. Data Nucl. Data Tables 14 613
Google Scholar
[6] Aufmuth P, Heilig K, Steudel A 1987 At. Data Nucl. Data Tables 37 455
Google Scholar
[7] Angeli I, Marinova K P 2013 At. Data Nucl. Data Tables 99 69
Google Scholar
[8] Nerlo-Pomorska B, Pomorski K 1993 Z. Phys. A 344 359
Google Scholar
[9] Nerlo-Pomorska B, Pomorski K 1994 Z. Phys. A 348 169
Google Scholar
[10] 圣宗强, 樊广伟, 钱建发 2015 64 112101
Google Scholar
Sheng Z Q, Fan G W, Qian J F 2015 Acta Phys. sin. 64 112101
Google Scholar
[11] 曾谨言 1957 13 357
Google Scholar
Zeng J Y 1957 Acta Phys. Sin. 13 357
Google Scholar
[12] 曾谨言 1975 24 151
Google Scholar
Zeng J Y 1975 Acta Phys. Sin. 24 151
Google Scholar
[13] 张双全, 孟杰, 周善贵, 曾谨言 2002 高能物理与核物理 26 252
Google Scholar
Zhang S Q, Meng J, Zhou S G, Zeng J Y 2002 High Energy Physics and Nuclear Physics 26 252
Google Scholar
[14] Barzakh A E, Fedorov D V, Ivanov V S, Molkanov P L, Moroz F V, Orlov S Y, Panteleev V N, Seliverstov M D, Volkov M Y 2018 Phys. Rev. C 97 014322
Google Scholar
[15] Yang J J, Piekarewicz J 2018 Phys. Rev. C 97 014314
Google Scholar
[16] Safronova M S, Porsev S G, Kozlov M G, Thielking J, Okhapkin M V, Glowacki P, Meier D M, Peik E 2018 Phys. Rev. Lett. 121 213001
Google Scholar
[17] Casten R F 1985 Phys. Rev. Lett. 54 1991
Google Scholar
[18] Casten R F, Brenner D S, Haustein P E 1987 Phys. Rev. Lett. 58 658
Google Scholar
[19] Casten R F 1988 J. Phys. G: Nucl. Part. Phys. 14 S71
Google Scholar
[20] Casten R F, Zamfir N V 1993 Phys. Rev. Lett. 70 402
Google Scholar
[21] Foy B D, Casten R F, Zamfir N V, Brenner D S 1994 Phys. Rev. C 49 1224
[22] Saha M, Sen S 1994 Phys. Rev. C 49 2460
[23] Gangopadhyar G 2009 J. Phys. G: Nucl. Part. Phys. 36 095105
Google Scholar
[24] Stopkowicz S, Gauss J 2014 Phys. Rev. A 90 022507
Google Scholar
[25] Zhao P W, Zhang S Q, Meng J 2014 Phys. Rev. C 89 011301
Google Scholar
[26] Otsuka T, Suzuki T, Fujimoto R, Grawe H, Akaish Y 2005 Phys. Rev. Lett. 95 232502
Google Scholar
[27] Bohr A 1976 Science 48 365
[28] Cheal B, Mane E, Billowes J, Bissell M L, Blaum K, Brown B A, Charlwood F C, Flanagan K T, Forest D H, Geppert C, Honma M, Jokinen A, Kowalska M, Krieger A, Kramer J, Moore I D, Neugart R, Neyens G, Nortershauser W, Schug M, Stroke H H, Vingerhoets P, Yordanov D T, Zakova M 2010 Phys. Rev. Lett. 104 202502
[29] Ohtsubo T, Stone N J, Stone J R, Towner I S, Bingham C R, Gaulard C, Koster U, Muto S, Nikolov J, Nishimura K, Simpson G S, Soti G, Veskovic M, Walters W B, Wauters F 2012 Phys. Rev. Lett. 109 032504
Google Scholar
[30] Snyder J B, Reviol W, Sarantites D G, Afanasjev A V, Janssens R V F, Abusara H, Carpenter M P, Chen X, Chiara C J, Greene J P, Lauritsen T, McCutchan E A, Seweryniak D, Zhu S 2013 Phys. Rev. B 723 61
[31] Heyde K, Wood J L 2011 Rev. Mod. Phys. 83 1467
Google Scholar
[32] Yordanov D T, Balabanski D L, Bieron J, Bissell M L, Blaum K, Budincevic I, Frizsche S, Frommgen N, Georgiev G 2013 Phys. Rev. Lett. 110 192501
Google Scholar
[33] 陈春杏 2015 硕士学位论文 (广西: 广西师范大学)
Chen C X 2015 M. S. Thesis (Guangxi: Guangxi Normal University) (in Chinese)
[34] Stone N J 2016 At. Data Nucl. Data Tables 111-112 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9883
- PDF Downloads: 249
- Cited By: 0
