Synchronization transition from bursting to spiking and bifurcation mechanism of the pre-Bötzinger complex

Yang Yong-Xia; Li Yu-Ye; Gu Hua-Guang

doi:10.7498/aps.69.20191509

Abstract

The pre-Bötzinger complex is a neuronal network with excitatory coupling, which participates in modulation of respiratory rhythms via the generation of complex firing rhythm patterns and synchronization transitions of rhythm patterns. In the present paper, a mathematical model of single neuron that exhibits complex transition processes from bursting to spiking is selected as a unit, the network model of the pre-Bötzinger complex composed of two neurons with excitatory coupling is constructed, multiple synchronous rhythm patterns and complex transition processes of the synchronous rhythm patterns related to the biological experimental observations are simulated, and the corresponding bifurcation mechanism is acquired with the fast-slow variable dissection method. When the initial values of two neurons of the pre-Bötzinger complex are the same, with increasing the excitatory coupling strength, the theoretical model of the pre-Bötzinger complex shows complete synchronization transition processes from "fold/homoclinic" bursting, to "subHopf/subHopf" bursting, and at last to period-1 spiking. When the initial values are different, with the increases of the excitatory coupling intensity, the rhythm transition processes begin from phase synchronization behaviors including "fold/homoclinic" bursting, "fold/fold limit cycle" bursting, mixed bursting composed of "subHopf/subHopf" bursting and "fold/fold limit cycle" bursting, and "subHopf/ subHopf" bursting in sequence, and to anti-phase synchronous behavior of the period-1 spiking. The complete (in-phase) synchronous period-1 spiking for the same initial values exhibits bifurcation mechanism different from the anti-phase synchronous period-1 spiking for different initial values. The anti-phase synchronous period-1 spiking presents a novel and abnormal example of the synchronization at large excitatory coupling strength, which is different from the traditional viewpoint that large excitatory coupling often induces in-phase synchronous behavior. The results present the synchronization transition process and complex bifurcation mechanism from bursting to period-1 spiking of the pre-Bötzinger complex, and the abnormal synchronization example enriches the contents of nonlinear dynamics.

Keywords:

Authors and contacts

1.
College of Mathematics and Computer Science, Chifeng University, Chifeng 024000, China
2.
Institute of Applied Mathematics, Chifeng University, Chifeng 024000, China
3.
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China

Corresponding author: Li Yu-Ye, liyuye2000@163.com

FullText HTML : translate this paragraph

References

[1]	Braun H A, Wissing H, Schäfer K, Hirsch M C 1994 Nature 367 270 Google Scholar
[2]	Gu H G, Pan B B 2015 Nonlinear Dyn. 81 2107 Google Scholar
[3]	谢勇, 程建慧 2017 66 090501 Google Scholar Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501 Google Scholar
[4]	Sun X J, Perc M, Kurths J, Lu Q S 2018 Chaos 28 106310 Google Scholar
[5]	徐莹, 王春妮, 靳伍银, 马军 2015 64 198701 Xu Y, Wang C N, Jin W Y, Ma J 2015 Acta Phys. Sin. 64 198701
[6]	李国芳, 孙晓娟 2017 66 240501 Google Scholar Li G F, Sun X J 2017 Acta Phys. Sin. 66 240501 Google Scholar
[7]	Bianchi A L, Denavit-Saubie M, Champagnat J 1995 Physiol. Rev. 75 1 Google Scholar
[8]	Cohen M I 1979 Physiol. Rev. 59 1105 Google Scholar
[9]	Funk G D, Smith J C, Feldman J L 1995 J. Neurosci. 15 4046 Google Scholar
[10]	Richter D W, Ballanyi K, Schwarzacher S 1992 Curr. Opin. Neurobiol. 2 788 Google Scholar
[11]	严亨秀, 张承武, 郑煜 2004 生理学报 56 665 Google Scholar Yan H X, Zhang C W, Zheng Y 2004 Acta Physiol. Sin. 56 665 Google Scholar
[12]	宋刚 1999 生理科学进展 3 237 Song G 1999 Prog. Physiol. Sci. 3 237
[13]	Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726 Google Scholar
[14]	Feldman J L, Negro C A D 2006 Nat. Rev. Neurosci. 7 232 Google Scholar
[15]	Smith J C 1997 Neurons, Networks, and Motor Behavior (Cambridge, MA: MIT Press) p97
[16]	Johnson S M, Smith J C, Funk G D, Feldman J L 1994 J. Neurophysiol. 72 2598 Google Scholar
[17]	Ramirez J M, Richter D W 1996 Curr. Opin. Neurobiol. 6 817 Google Scholar
[18]	Rekling J C, Feldman J L 1998 Annu. Rev. Physiol. 60 385 Google Scholar
[19]	Koshiya N, Smith J C 1998 28^th Annual Meeting of the Society for Neuroscience Los Angeles, California, USA, November 7-12, 1998 p531
[20]	Koshiya N, Smith J C 1999 Nature 400 360 Google Scholar
[21]	Negro C A D, Morgado V C, Hayes J A, Mackay D D, Pace R W, Crowder E A, Feldman J L 2005 J. Neurosci. 25 446 Google Scholar
[22]	Smith J C, Butera R J, Koshiya N, Del Negro C, Wilson C G, Johnson S M 2000 Resp. Physiol. 122 131 Google Scholar
[23]	Gray P A, Rekling J C, Bocchiaro C M, Feldman J L 1999 Science 286 1566 Google Scholar
[24]	Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 382 Google Scholar
[25]	Dunmyre J R, Negro C A D, Rubin J E 2011 J. Comput. Neurosci. 31 305 Google Scholar
[26]	Negro C A D, Johnson S M, Butera R J, Smith J C 2001 J. Neurophysiol. 86 59 Google Scholar
[27]	Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 398 Google Scholar
[28]	Purvis L K, Smith J C, Koizumi H, Butera R J 2007 J. Neurophysiol. 97 1515 Google Scholar
[29]	Best J, Borisyuk A, Rubin J E, Terman D, Wechselberger M 2005 SIAM J. Appl. Dyn. Syst. 4 1107 Google Scholar
[30]	Rubin J E 2006 Phys. Rev. E 74 021917 Google Scholar
[31]	Dunmyre J R, Rubin J E 2010 SIAM J Appl. Dyn. Syst. 9 154 Google Scholar
[32]	Guo D D, Lü Z S 2019 Chin. Phys. B 28 110501 Google Scholar
[33]	Rybak I A, Molkov Y I, Jasinski P E, Shevtsova N A, Smith J C 2014 Prog. Brain. Res. 209 1 Google Scholar
[34]	张应腾, 熊冬生, 刘深泉 2015 中国医学物理学杂志 32 115 Google Scholar Zhang Y T, Xiong D S, Liu S Q 2015 Chin. J. Med. Phys. 32 115 Google Scholar
[35]	刘义, 刘深泉 2011 动力学与控制学报 9 257 Google Scholar Liu Y, Liu S Q 2011 J. Dynam. Cont. 9 257 Google Scholar
[36]	Duan L X, Zhai D H, Tang X H 2012 Int. J. Bifurcation Chaos 22 1250114 Google Scholar
[37]	Lü Z S, Chen L N, Duan L X 2019 Appl. Math. Model. 67 234 Google Scholar
[38]	Lü Z S, Zhang B Z, Duan L X 2017 Cogn. Neurodynamics 11 443 Google Scholar
[39]	Wang Z J, Duan L X, Cao Q Y 2018 Chin. Phys. B 27 070502 Google Scholar
[40]	Duan L X, Liu J, Chen X, Xiao P C, Zhao Y 2017 Cogn. Neurodynamics 11 91 Google Scholar
[41]	Rubin J E, Shevtsova N A, Ermentrout G B, Smith J C, Rybak I A 2009 J. Neurophysiol. 101 2146 Google Scholar
[42]	Rubin J E, Bacak B J, Molkov Y I, Shevtsova N A, Smith J C, Rybak I A 2011 J. Comput. Neurosci. 30 607 Google Scholar
[43]	平小方, 刘深泉, 任会霞 2015 动力学与控制学报 13 215 Google Scholar Ping X F, Liu S Q, Ren H X 2015 J. Dynam. Cont. 13 215 Google Scholar
[44]	Belykh I, Shilnikov A 2008 Phys. Rev. Lett. 101 078102 Google Scholar
[45]	Wu F Q, Gu H G, Li Y Y 2019 Commun. Nonlinear Sci. Numer. Simul. 79 104924 Google Scholar
[46]	丁学利, 李玉叶 2016 65 210502 Google Scholar Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502 Google Scholar
[47]	Jia B, Wu Y C, He D, Guo B H, Xue L 2018 Nonlinear Dyn. 93 1599 Google Scholar
[48]	Li Y Y, Gu H G, Ding X L 2019 Nonlinear Dyn. 97 2091 Google Scholar
[49]	曹奔, 关利南, 古华光 2018 67 240502 Google Scholar Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502 Google Scholar
[50]	Uzuntarla M, Torres J J, Calim A, Barreto E 2019 Neural Networks 110 131 Google Scholar
[51]	埃门创特 B 著 (孝鹏程, 段丽霞, 苏建忠译) 2002 动力系统仿真, 分析与动画—XPPAUT使用指南 (北京: 科学出版社) 第155−167页 Ermentrout B (translated by Xiao P C, Duan L L, Su J Z) 2002 Simulating, Analyzing, and Animating Dynamical systems: A Guide to XPPAUT for Researchers and Students (Beijing: Science Press) p155−167 (in Chinese)
[52]	Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171 Google Scholar
[53]	Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917 Google Scholar
[54]	Jia B, Gu H G 2017 Int. J. Bifurcation Chaos 27 1750113 Google Scholar
[55]	Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760 Google Scholar
[56]	Li J J, Du M M, Wang R, Lei J Z, Wu Y 2016 Int. J. Bifurcation Chaos 26 1650138 Google Scholar

Cited By

图 1 不同${g_{\rm{K}}}$下单神经元放电在(h, V)相平面的轨迹　(a) $ {g_{\rm{K}}} = {\rm{7}}{\rm{.1}}\;{\rm{nS}} $; (b) $ {g_{\rm{K}}} = {\rm{7}}{\rm{.8}}\;{\rm{nS}} $; (c) $ {g_{\rm{K}}} = {\rm{10}}{\rm{.0}}\;{\rm{nS}} $; (d) $ {g_{\rm{K}}} = {\rm{25}}{\rm{.0}}\;{\rm{nS}} $

Figure 1. The (h, V) trajectory of the single neuron at different ${g_{\rm{K}}}$ values: (a) $ {g_{\rm{K}}} = {\rm{7}}{\rm{.1}}\;{\rm{nS}} $; (b) $ {g_{\rm{K}}} = {\rm{7}}{\rm{.8}}\;{\rm{nS}} $; (c) $ {g_{\rm{K}}} = {\rm{10}}{\rm{.0}}\;{\rm{nS}} $; (d) $ {g_{\rm{K}}} = {\rm{25}}{\rm{.0}}\;{\rm{nS}} $.

DownLoad: Full-Size Img PowerPoint

图 2 单神经元模型的随${g_{\rm{K}}}$的分岔　(a) ISIs分岔序列; (b)图(a)左下角方框的局部放大

Figure 2. Bifurcation of the single neuron model with increasing ${g_{\rm{K}}}$: (a) Bifurcations of ISIs; (b) the enlargement of ISIs within the square at the down-left corner of fig (a).

DownLoad: Full-Size Img PowerPoint

图 3 当$ {g_{\rm{K}}} = 7.1\;{\rm{nS}} $时, 单神经元模型的快子系统随着慢变量h变化的分岔

Figure 3. Bifurcations of the fast-subsystem of the single neuron with respect to h when $ {g_{\rm{K}}} = 7.1\;{\rm{nS}} $.

DownLoad: Full-Size Img PowerPoint

图 4 单神经元在不同的${g_{\rm{K}}}$下簇放电模式的快慢变量分离　(a) $ {g_{\rm{K}}} = {\rm{7}}.1\;{\rm{nS}} $; (b) $ {g_{\rm{K}}} = {\rm{7}}.8\;{\rm{nS}} $; (c) $ {g_{\rm{K}}} = {\rm{10}}.0\;{\rm{nS}} $; (d) ${g_{\rm{K}}} =$ 25.0 nS

Figure 4. The fast-slow variable dissection of bursting of single neuron at different ${g_{\rm{K}}}$ values: (a) $ {g_{\rm{K}}} = {\rm{7}}.1\;{\rm{nS}} $; (b) $ {g_{\rm{K}}} = {\rm{7}}.8\;{\rm{nS}} $; (c) $ {g_{\rm{K}}} = {\rm{10}}.0\;{\rm{nS}} $; (d) $ {g_{\rm{K}}} = {\rm{25}}.0\;{\rm{nS}} $.

DownLoad: Full-Size Img PowerPoint

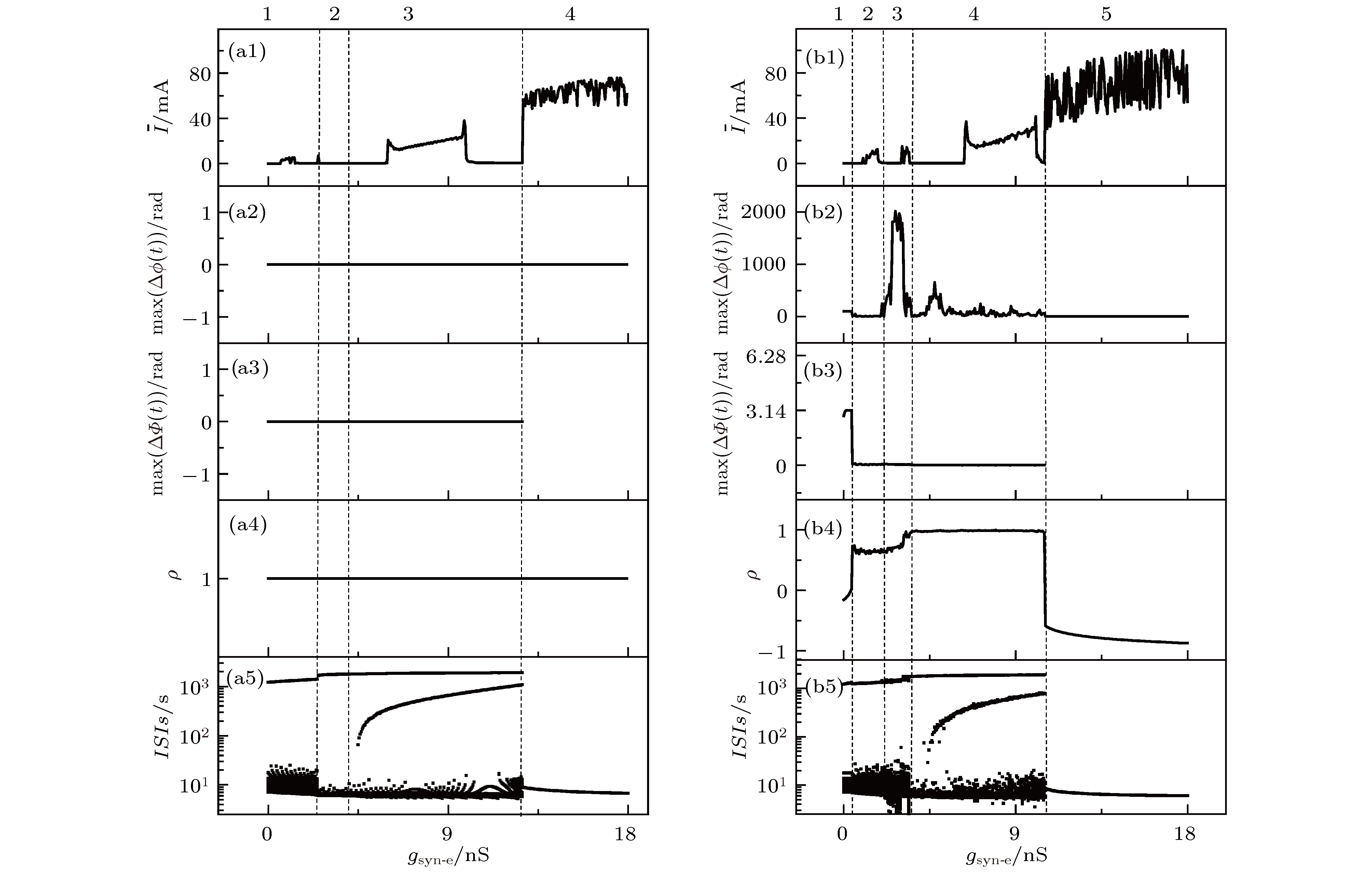
图 5 随着耦合强度${g_{{\text{syn-e}}}}$增大, 耦合神经元模型的同步转迁过程. 相同初值　(a1)耦合电流平均值$\bar I$; (a2)峰相位差的最大值$\max (\Delta (\phi (t)))$; (a3)簇相位差的最大值$ \max (\Delta (\varPhi (t))) $; (a4)相关系数ρ; (a5)神经元1的ISIs序列. 不同初值: (b1)耦合电流平均值$\bar I$; (b2)峰相位差的最大值$\max (\Delta (\phi (t)))$; (b3)簇相位差的最大值$ \max (\Delta (\varPhi (t))) $; (b4)相关系数ρ; (b5)神经元1的ISIs序列

Figure 5. Transitions with respect to ${g_{{\text{syn-e}}}}$ of coupled neurons model. The same initial values: (a1) The mean values of coupling current $\bar I$; (a2) maximum spike phase difference $\max (\Delta (\phi (t)))$; (a3) maximum burst phase difference $ \max (\Delta (\varPhi (t))) $; (a4) coefficient ρ; (a5) ISIs of neuron 1. Different initial values: (b1) The mean values of coupling current $\bar I$; (b2) maximum spike phase difference $\max (\Delta (\phi (t)))$; (b3) maximum burst phase difference $ \max (\Delta (\varPhi (t))) $; (b4) coefficient ρ; (b5) ISIs of neuron 1.

DownLoad: Full-Size Img PowerPoint

图 6 初值相同时, 不同耦合强度下神经元1(红)和2(蓝)的膜电位$V$(上)及耦合电流${I^{{\text{syn-e}}}}$ (下), 插图是局部放大　(a) $ {g_{{\text{syn-e}}}} = {\rm{0}}{\rm{.35}}\;{\rm{nS}} $; (b) $ {g_{{\text{syn-e}}}} = {\rm{2}}{\rm{.5}}\;{\rm{nS}} $; (c) $ {g_{{\text{syn-e}}}} = {\rm{5}}{\rm{.0}}\;{\rm{nS}} $; (d) $ {g_{{\text{syn-e}}}} = {\rm{18}}{\rm{.0}}\;{\rm{nS}} $

Figure 6. Membrane potential $V$ (top) and coupling current ${I^{{\text{syn-e}}}}$ (low) of neurons 1 (red) and 2 (blue) with the same initial values at different ${g_{{\text{syn-e}}}}$ values (Insert figure: the enlargement of bursting): (a) $ {g_{{\text{syn-e}}}} = {\rm{0}}{\rm{.35}}\;{\rm{nS}} $; (b) $ {g_{{\text{syn-e}}}} = {\rm{2}}{\rm{.5}}\;{\rm{nS}} $; (c) $ {g_{{\text{syn-e}}}} = {\rm{5}}{\rm{.0}}\;{\rm{nS}} $; (d) $ {g_{{\text{syn-e}}}} = {\rm{18}}{\rm{.0}}\;{\rm{nS}} $.

DownLoad: Full-Size Img PowerPoint

图 7 初值不同时, 不同耦合强度下神经元1(红)和2(蓝)的膜电位V(上)及耦合电流${I^{{\text{syn-e}}}}$ (下), 插图是局部放大　(a) $g_\text{syn-e}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 1.5 nS (c) $g_\text{syn-e}$ = 2.5 nS; (d) $g_\text{syn-e}$ = 5.0 nS; (e) $g_\text{syn-e}$ = 18.0 nS

Figure 7. Membrane potential V (top) and coupling current ${I^{{\text{syn-e}}}}$ (low) of neurons 1 (red) and 2 (blue) with different initial values at different $g_\text{syn-e}$ (Insert figure: the enlargement of bursting): (a) $g_\text{syn-e}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 1.5 nS; (c) $g_\text{syn-e}$ = 2.5 nS; (d) $g_\text{syn-e}$ = 5.0 nS; (e) $g_\text{syn-e}$ = 18.0 nS.

DownLoad: Full-Size Img PowerPoint

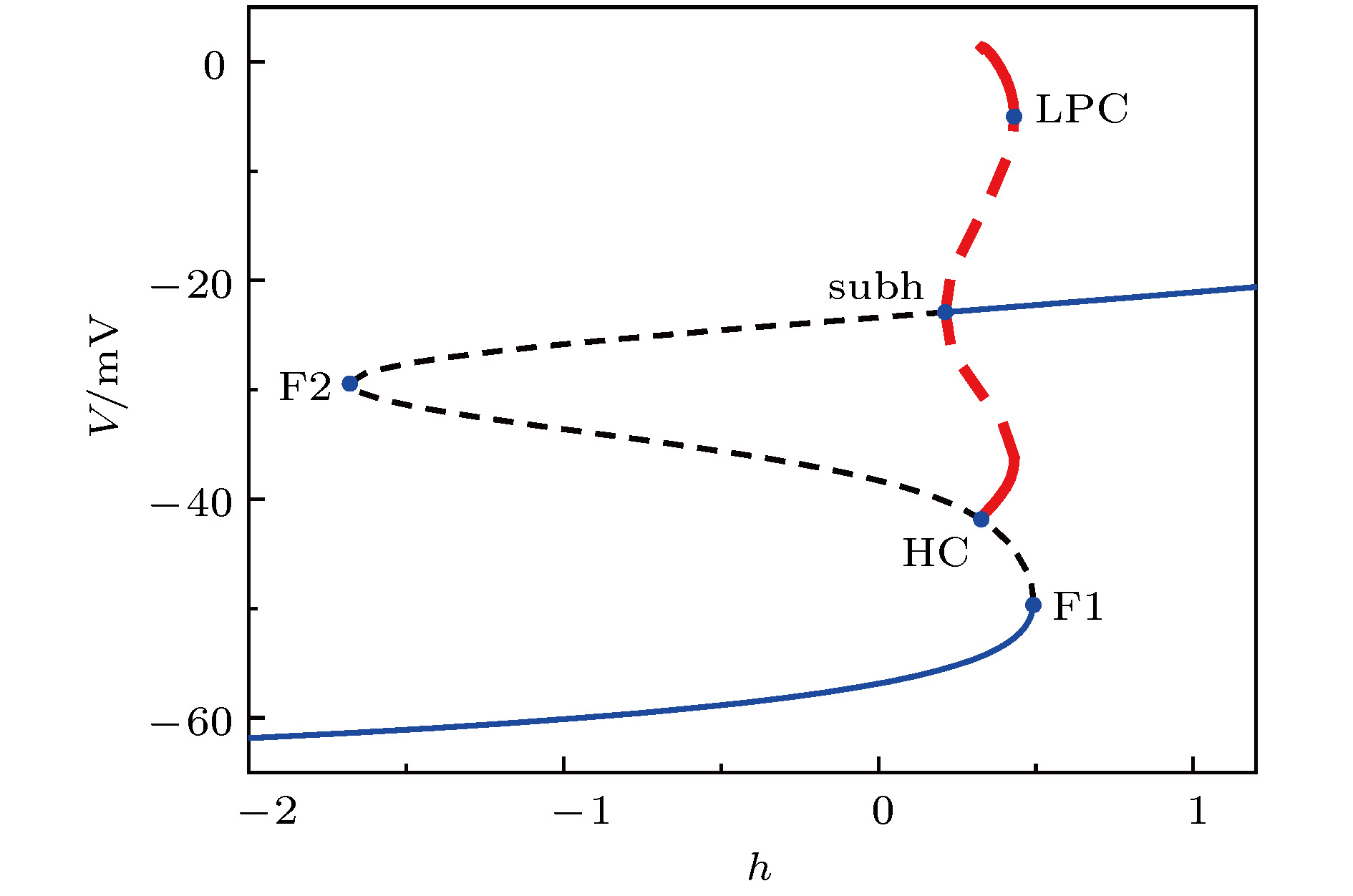
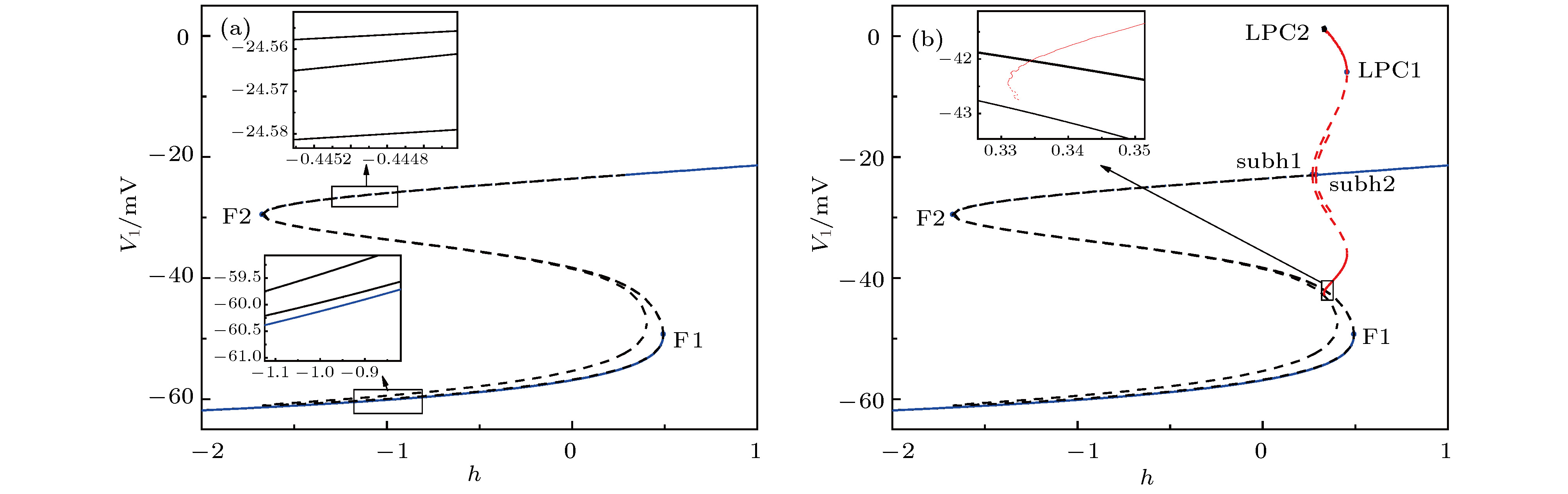
图 8 当$g_\text{syn-e}$ = 1.5 nS时, 两耦合神经元的快子系统的分岔, 插图是局部放大　(a)平衡点分岔; (b)平衡点分岔和极限环的分岔

Figure 8. Bifurcations of the fast-subsystem of the two coupled neurons with respect to h when $g_\text{syn-e}$ = 1.5 nS (Insert figure: the enlargement): (a) Equilibrium points; (b) equilibrium points and limit cycle.

DownLoad: Full-Size Img PowerPoint

图 9 初值相同时, 神经元1在不同耦合强度下簇放电模式的快慢变量分离, 插图是局部放大　(a) $g_\text{syn-e}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 2.5 nS; (c) $g_\text{syn-e}$ = 5.0 nS; (d) $g_\text{syn-e}$ = 18.0 nS

Figure 9. The fast-slow variable dissection of neuron 1 for different initial values at different $g_\text{syn-e}$ values (Insert figure: the enlargement): (a) $g_\text{syn-e}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 2.5 nS; (c) $g_\text{syn-e}$ = 5.0 nS; (d) $g_\text{syn-e}$ = 18.0 nS.

DownLoad: Full-Size Img PowerPoint

图 10 初值不同时, 神经元1在不同耦合强度下簇放电模式的快慢变量分离, 插图是局部放大　(a) ${g_{{\rm{syn - e}}}}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 1.5 nS; (c)和(d) $g_\text{syn-e}$ = 2.5 nS; (e) $g_\text{syn-e}$ = 5.0 nS; (f) $g_\text{syn-e}$ = 18.0 nS

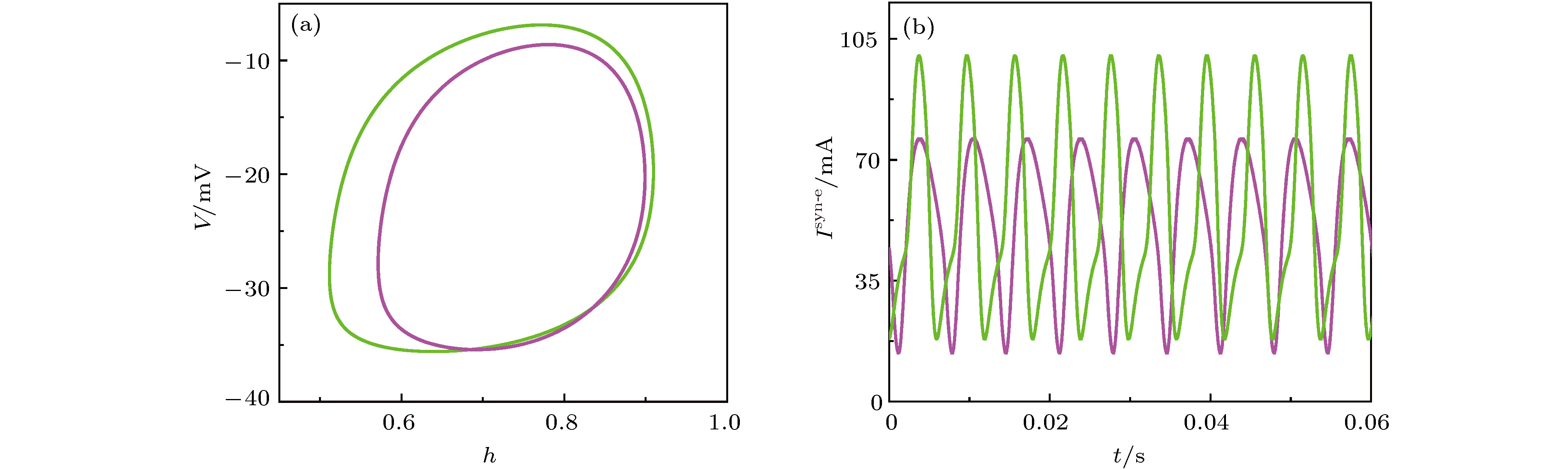
Figure 10. The fast-slow variable dissection of neuron 1 for different initial values at different $g_\text{syn-e}$ values (Insert figure: the enlargement): (a)$g_\text{syn-e}$ = 0.35 nS; (b) $g_\text{syn-e}$ = 1.5 nS; (c) and (d) $g_\text{syn-e}$ = 2.5 nS; (e) $g_\text{syn-e}$ = 5.0 nS; (f) $g_\text{syn-e}$ = 18.0 nS.

DownLoad: Full-Size Img PowerPoint

图 11 反相同步(紫色)和同相同步(绿色)周期1峰放电节律　(a) (h, V₁)相平面上的相轨迹图; (b)耦合电流随时间t的变化

Figure 11. The anti-phase (purple) and in-phase (green) period-1 spiking: (a) The V-h trajectory; (b) coupling current.

DownLoad: Full-Size Img PowerPoint

图 12 (a)快子系统的平衡点和极限环的分岔; (b)图(a)中极限环分岔处的放大; (c)反相同步(紫色)和同相同步(绿色)周期1峰放电的快慢变量分离; (d)图(c)中反向同步(紫色)和同向(绿色)同步周期1峰放电的放大

Figure 12. (a) Bifurcations of equilibrium points and limit cycle of the fast-subsystem; (b) enlargement of (a); (c) fast-slow variable dissection of anti-phase (purple) and in-phase (green) period-1 spiking; (d) enlargement of anti-phase (purple) and in-phase (green) period-1 spiking in Fig. (c).

DownLoad: Full-Size Img PowerPoint

表 1 理论模型中的参数值

Table 1. Parameter values used in the theoretical model.

参数	参数值	参数	参数值	参数	参数值	参数	参数值
C	21 pF	$ {\sigma _{ {\rm{m_p} }} } $	–6 mV	$ {g_{ {\rm{Nap} }} } $	2.8 nS	${E_{{\rm{Na}}}}$	50 mV
$ {\theta _{ {\rm{m_p} }} } $	–40 mV	${\sigma _{\rm{m}}}$	–5 mV	${g_{{\rm{Na}}}}$	28 nS	${E_{\rm{K}}}$	–85 mV
${\theta _{\rm{m}}}$	–34 mV	$\sigma {}_{\rm{h}}$	6 mV	${g_{\rm{L}}}$	2.8 nS	${E_{\rm{L}}}$	–65 mV
${\theta _{\rm{h}}}$	–48 mV	${\sigma _{\rm{n}}}$	–4 mV	${g_{ {\text{tonic-e} } } }$	0.4 nS	${\bar \tau _{\rm{h}}}$	10000 ms
${\theta _{\rm{n}}}$	–29 mV	${\sigma _{\rm{s}}}$	–5 mV	${\varepsilon _{}}$	6	${\bar \tau _{\rm{n}}}$	5 ms
$\theta {}_{\rm{s}}$	–10 mV	${\alpha _{\rm{s}}}$	–5 mV

DownLoad: CSV

表 2 不同${g_{\rm{K}}}$下快子系统中关键点的慢变量h的值

Table 2. The values of slow variable h of the bifurcation or key points at different ${g_{\rm{K}}}$ values.

关键点	h的值
关键点	F1	F2	subh	HC	LPC	共存区域
$ {g_{\rm{K} }} = 7.1\;{\rm{nS}} $	0.4928	–1.6780	0.2128	0.3265	0.4308	[0.3265, 0.4308]
$ {g_{\rm{K} }} = 7.8\;{\rm{nS}} $	0.4928	–1.6680	0.2858	0.3476	0.4973	[0.3476, 0.4928]
$ {g_{\rm{K} }} = 10.0 \;{\rm{nS}} $	0.4928	–1.6390	0.5072	0.3941	0.7025	[0.3941, 0.4928]
$ {g_{\rm{K} }} = 25.0 \;{\rm{nS}} $	0.4928	–1.4800	1.7880	0.4849	1.9240	[0.4849, 0.4928]

DownLoad: CSV

表 3 不同${g_{{\rm{syn\text-e}}}}$下快子系统中关键点的慢变量h的值

Table 3. The slow variable h values of the bifurcation or key points at different ${g_{{\rm{syn\text-e}}}}$ values.

关键点	h的值
关键点	$g_\text{syn-e}$ = 0.35 nS	$g_\text{syn-e}$ = 2.5 nS	$g_\text{syn-e}$ = 5.0 nS	$g_\text{syn-e}$ = 18.0 nS
F1	0.4874	0.4918	0.4908	0.4856
F2	–1.6695	–1.6759	–1.6685	–1.7212
subh1	0.2817	0.2565	0.2259	0.0746
subh2	0.2858	0.2852	0.2274	0.0794
LPC1	0.4927	0.4273	0.3598	0.0960
LPC2	\	0.3103	0.2406	–0.2504
LPC3	\	\	\	0.0890
LPC4	\	\	\	–0.099
HC	0.3398	\	\	\
共存区域	[0.3398, 0.4927]	[0.3103, 0.4273]	[0.2406, 0.3598]	[0.0960, 0.250]和[0.0890, 0.099]

DownLoad: CSV

map

[1]	Braun H A, Wissing H, Schäfer K, Hirsch M C 1994 Nature 367 270 Google Scholar
[2]	Gu H G, Pan B B 2015 Nonlinear Dyn. 81 2107 Google Scholar
[3]	谢勇, 程建慧 2017 66 090501 Google Scholar Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501 Google Scholar
[4]	Sun X J, Perc M, Kurths J, Lu Q S 2018 Chaos 28 106310 Google Scholar
[5]	徐莹, 王春妮, 靳伍银, 马军 2015 64 198701 Xu Y, Wang C N, Jin W Y, Ma J 2015 Acta Phys. Sin. 64 198701
[6]	李国芳, 孙晓娟 2017 66 240501 Google Scholar Li G F, Sun X J 2017 Acta Phys. Sin. 66 240501 Google Scholar
[7]	Bianchi A L, Denavit-Saubie M, Champagnat J 1995 Physiol. Rev. 75 1 Google Scholar
[8]	Cohen M I 1979 Physiol. Rev. 59 1105 Google Scholar
[9]	Funk G D, Smith J C, Feldman J L 1995 J. Neurosci. 15 4046 Google Scholar
[10]	Richter D W, Ballanyi K, Schwarzacher S 1992 Curr. Opin. Neurobiol. 2 788 Google Scholar
[11]	严亨秀, 张承武, 郑煜 2004 生理学报 56 665 Google Scholar Yan H X, Zhang C W, Zheng Y 2004 Acta Physiol. Sin. 56 665 Google Scholar
[12]	宋刚 1999 生理科学进展 3 237 Song G 1999 Prog. Physiol. Sci. 3 237
[13]	Smith J C, Ellenberger H H, Ballanyi K, Richter D W, Feldman J L 1991 Science 254 726 Google Scholar
[14]	Feldman J L, Negro C A D 2006 Nat. Rev. Neurosci. 7 232 Google Scholar
[15]	Smith J C 1997 Neurons, Networks, and Motor Behavior (Cambridge, MA: MIT Press) p97
[16]	Johnson S M, Smith J C, Funk G D, Feldman J L 1994 J. Neurophysiol. 72 2598 Google Scholar
[17]	Ramirez J M, Richter D W 1996 Curr. Opin. Neurobiol. 6 817 Google Scholar
[18]	Rekling J C, Feldman J L 1998 Annu. Rev. Physiol. 60 385 Google Scholar
[19]	Koshiya N, Smith J C 1998 28^th Annual Meeting of the Society for Neuroscience Los Angeles, California, USA, November 7-12, 1998 p531
[20]	Koshiya N, Smith J C 1999 Nature 400 360 Google Scholar
[21]	Negro C A D, Morgado V C, Hayes J A, Mackay D D, Pace R W, Crowder E A, Feldman J L 2005 J. Neurosci. 25 446 Google Scholar
[22]	Smith J C, Butera R J, Koshiya N, Del Negro C, Wilson C G, Johnson S M 2000 Resp. Physiol. 122 131 Google Scholar
[23]	Gray P A, Rekling J C, Bocchiaro C M, Feldman J L 1999 Science 286 1566 Google Scholar
[24]	Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 382 Google Scholar
[25]	Dunmyre J R, Negro C A D, Rubin J E 2011 J. Comput. Neurosci. 31 305 Google Scholar
[26]	Negro C A D, Johnson S M, Butera R J, Smith J C 2001 J. Neurophysiol. 86 59 Google Scholar
[27]	Butera R J, Rinzel J, Smith J C 1999 J. Neurophysiol. 82 398 Google Scholar
[28]	Purvis L K, Smith J C, Koizumi H, Butera R J 2007 J. Neurophysiol. 97 1515 Google Scholar
[29]	Best J, Borisyuk A, Rubin J E, Terman D, Wechselberger M 2005 SIAM J. Appl. Dyn. Syst. 4 1107 Google Scholar
[30]	Rubin J E 2006 Phys. Rev. E 74 021917 Google Scholar
[31]	Dunmyre J R, Rubin J E 2010 SIAM J Appl. Dyn. Syst. 9 154 Google Scholar
[32]	Guo D D, Lü Z S 2019 Chin. Phys. B 28 110501 Google Scholar
[33]	Rybak I A, Molkov Y I, Jasinski P E, Shevtsova N A, Smith J C 2014 Prog. Brain. Res. 209 1 Google Scholar
[34]	张应腾, 熊冬生, 刘深泉 2015 中国医学物理学杂志 32 115 Google Scholar Zhang Y T, Xiong D S, Liu S Q 2015 Chin. J. Med. Phys. 32 115 Google Scholar
[35]	刘义, 刘深泉 2011 动力学与控制学报 9 257 Google Scholar Liu Y, Liu S Q 2011 J. Dynam. Cont. 9 257 Google Scholar
[36]	Duan L X, Zhai D H, Tang X H 2012 Int. J. Bifurcation Chaos 22 1250114 Google Scholar
[37]	Lü Z S, Chen L N, Duan L X 2019 Appl. Math. Model. 67 234 Google Scholar
[38]	Lü Z S, Zhang B Z, Duan L X 2017 Cogn. Neurodynamics 11 443 Google Scholar
[39]	Wang Z J, Duan L X, Cao Q Y 2018 Chin. Phys. B 27 070502 Google Scholar
[40]	Duan L X, Liu J, Chen X, Xiao P C, Zhao Y 2017 Cogn. Neurodynamics 11 91 Google Scholar
[41]	Rubin J E, Shevtsova N A, Ermentrout G B, Smith J C, Rybak I A 2009 J. Neurophysiol. 101 2146 Google Scholar
[42]	Rubin J E, Bacak B J, Molkov Y I, Shevtsova N A, Smith J C, Rybak I A 2011 J. Comput. Neurosci. 30 607 Google Scholar
[43]	平小方, 刘深泉, 任会霞 2015 动力学与控制学报 13 215 Google Scholar Ping X F, Liu S Q, Ren H X 2015 J. Dynam. Cont. 13 215 Google Scholar
[44]	Belykh I, Shilnikov A 2008 Phys. Rev. Lett. 101 078102 Google Scholar
[45]	Wu F Q, Gu H G, Li Y Y 2019 Commun. Nonlinear Sci. Numer. Simul. 79 104924 Google Scholar
[46]	丁学利, 李玉叶 2016 65 210502 Google Scholar Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502 Google Scholar
[47]	Jia B, Wu Y C, He D, Guo B H, Xue L 2018 Nonlinear Dyn. 93 1599 Google Scholar
[48]	Li Y Y, Gu H G, Ding X L 2019 Nonlinear Dyn. 97 2091 Google Scholar
[49]	曹奔, 关利南, 古华光 2018 67 240502 Google Scholar Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502 Google Scholar
[50]	Uzuntarla M, Torres J J, Calim A, Barreto E 2019 Neural Networks 110 131 Google Scholar
[51]	埃门创特 B 著 (孝鹏程, 段丽霞, 苏建忠译) 2002 动力系统仿真, 分析与动画—XPPAUT使用指南 (北京: 科学出版社) 第155−167页 Ermentrout B (translated by Xiao P C, Duan L L, Su J Z) 2002 Simulating, Analyzing, and Animating Dynamical systems: A Guide to XPPAUT for Researchers and Students (Beijing: Science Press) p155−167 (in Chinese)
[52]	Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171 Google Scholar
[53]	Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917 Google Scholar
[54]	Jia B, Gu H G 2017 Int. J. Bifurcation Chaos 27 1750113 Google Scholar
[55]	Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760 Google Scholar
[56]	Li J J, Du M M, Wang R, Lei J Z, Wu Y 2016 Int. J. Bifurcation Chaos 26 1650138 Google Scholar

[1]	Liang Yan-Mei, Lu Bo, Gu Hua-Guang. Analysis to dynamics of complex electrical activities in Wilson model of brain neocortical neuron using fast-slow variable dissection with two slow variables. Acta Physica Sinica, 2022, 71(23): 230502. doi: 10.7498/aps.71.20221416
[2]	Li Li, Zhao Zhi-Guo, Gu Hua-Guang. Suppression effects of excitatory and inhibitory self-feedbacks on neuronal spiking near Hopf bifurcation. Acta Physica Sinica, 2022, 71(5): 050504. doi: 10.7498/aps.71.20211829
[3]	Xie Ying, Zhu Zhi-Gang, Zhang Xiao-Feng, Ren Guo-Dong. Control of firing mode in nonlinear neuron circuit driven by photocurrent. Acta Physica Sinica, 2021, 70(21): 210502. doi: 10.7498/aps.70.20210676
[4]	Ding Xue-Li, Gu Hua-Guang, Jia Bing, Li Yu-Ye. Anticipated synchronization of electrical activity induced by inhibitory autapse in coupled Morris-Lecar neuron model. Acta Physica Sinica, 2021, 70(21): 218701. doi: 10.7498/aps.70.20210912
[5]	Jiang Yi-Lan, Lu Bo, Zhang Wan-Qin, Gu Hua-Guang. Fast autaptic feedback induced-paradoxical changes of mixed-mode bursting and bifurcation mechanism. Acta Physica Sinica, 2021, 70(17): 170501. doi: 10.7498/aps.70.20210208
[6]	Zhao Ya-Qi, Liu Mou-Tian, Zhao Yong, Duan Li-Xia. Dynamics of mixed bursting in coupled pre-Bötzinger complex. Acta Physica Sinica, 2021, 70(12): 120501. doi: 10.7498/aps.70.20210093
[7]	Zheng Zhi-Gang, Zhai Yun, Wang Xue-Bin, Chen Hong-Bin, Xu Can. Synchronization of coupled phase oscillators: Order parameter theory. Acta Physica Sinica, 2020, 69(8): 080502. doi: 10.7498/aps.69.20191968
[8]	Hua Hong-Tao, Lu Bo, Gu Hua-Guang. Nonlinear mechanism of excitatory autapse-induced reduction or enhancement of firing frequency of neuronal bursting. Acta Physica Sinica, 2020, 69(9): 090502. doi: 10.7498/aps.69.20191709
[9]	Cao Ben, Guan Li-Nan, Gu Hua-Guang. Bifurcation mechanism of not increase but decrease of spike number within a neural burst induced by excitatory effect. Acta Physica Sinica, 2018, 67(24): 240502. doi: 10.7498/aps.67.20181675
[10]	Zheng Dian-Chun, Ding Ning, Shen Xiang-Dong, Zhao Da-Wei, Zheng Qiu-Ping, Wei Hong-Qing. Study on discharge phenomena of short-air-gap in needle-plate electrode based on fractal theory. Acta Physica Sinica, 2016, 65(2): 024703. doi: 10.7498/aps.65.024703
[11]	Ding Xue-Li, Li Yu-Ye. Period-adding bifurcation of neural firings induced by inhibitory autapses with time-delay. Acta Physica Sinica, 2016, 65(21): 210502. doi: 10.7498/aps.65.210502
[12]	Xiang Jun-Jie, Bi Chuang, Xiang Yong, Zhang Qian, Wang Jing-Mei. Dynamical study of peak-current-mode controlled synchronous switching Z-source converter. Acta Physica Sinica, 2014, 63(12): 120507. doi: 10.7498/aps.63.120507
[13]	Huang Chen, Chen Long, Bi Qin-Sheng, Jiang Hao-Bin. Vehicle negotiation model and bifurcation dynamic characteristics research. Acta Physica Sinica, 2013, 62(21): 210507. doi: 10.7498/aps.62.210507
[14]	Wang Fu-Xia, Xie Yong. Synchronization of "Hopf/homoclinic" bursting with "SubHopf/homoclinic" bursting. Acta Physica Sinica, 2013, 62(2): 020509. doi: 10.7498/aps.62.020509
[15]	Li Qun-Hong, Yan Yu-Long, Yang Dan. Bifurcations in coupled electrical circuit systems. Acta Physica Sinica, 2012, 61(20): 200505. doi: 10.7498/aps.61.200505
[16]	Gu Hua-Guang, Xi Lei, Jia Bing. Identification of a stochastic neural firing rhythm lying in period-adding bifurcation and resembling chaos. Acta Physica Sinica, 2012, 61(8): 080504. doi: 10.7498/aps.61.080504
[17]	Gu Hua-Guang, Zhu Zhou, Jia Bing. Dynamics of a novel chaotic neural firing pattern discovered in experiment and simulated in mathematical model. Acta Physica Sinica, 2011, 60(10): 100505. doi: 10.7498/aps.60.100505
[18]	Chen Zhang-Yao, Bi Qin-Sheng. Bifurcations and chaos of coupled Jerk systems. Acta Physica Sinica, 2010, 59(11): 7669-7678. doi: 10.7498/aps.59.7669
[19]	Bao Bo-Cheng, Kang Zhu-Sheng, Xu Jian-Ping, Hu Wen. Bifurcation and attractor of generalized square map with exponential term. Acta Physica Sinica, 2009, 58(3): 1420-1431. doi: 10.7498/aps.58.1420
[20]	Zhang Wei, Zhou Shu-Hua, Ren Yong, Shan Xiu-Ming. Bifurcation analysis and control in Turbo decoding algorithm. Acta Physica Sinica, 2006, 55(2): 622-627. doi: 10.7498/aps.55.622

Catalog

Vol. 69, Issue 4 - 2020-02-20

Metrics

Abstract views: 7850
PDF Downloads: 114
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板