耦合相振子系统同步的序参量理论

郑志刚; 翟云; 王学彬; 陈宏斌; 徐灿

doi:10.7498/aps.69.20191968

摘要

节律行为, 即系统行为呈现随时间的周期变化, 在我们的周围随处可见. 不同节律之间可以通过相互影响、相互作用产生自组织, 其中同步是最典型、最直接的有序行为, 它也是非线性波、斑图、集群行为等的物理内在机制. 不同的节律可以用具有不同频率的振子(极限环)来刻画, 它们之间的同步可以用耦合极限环系统的动力学来加以研究. 微观动力学表明, 随着耦合强度增强, 振子同步伴随着动力学状态空间降维到一个低维子空间, 该空间由序参量来描述. 序参量的涌现及其所描述的宏观动力学行为可借助于协同学与流形理论等降维思想来进行. 本文从统计物理学的角度讨论了耦合振子系统序参量涌现的几种降维方案, 并对它们进行了对比分析. 序参量理论可有效应用于耦合振子系统的同步自组织与相变现象的分析, 通过进一步研究序参量的动力学及其分岔行为, 可以对复杂系统的涌现动力学有更为深刻的理解.

关键词:

同步 /
序参量 /
涌现 /
分岔

Abstract

Rhythmic behaviors, i.e. temporally periodic oscillations in a system, can be ubiquitously found in nature. Interactions among various rhythms can lead to self-organized behaviors and synchronizations. This mechanism is also responsible for many phenomena such as nonlinear waves, spatiotemporal patterns, and collective behaviors in populations emerging in complex systems. Mathematically different oscillations are described by limit-cycle oscillators (pacemakers) with different intrinsic frequencies, and the synchrony of these units can be described by the dynamics of coupled oscillators. Studies of microscopic dynamics reveal that the emergence of synchronization manifests itself as the dimension reduction of phase space, indicating that synchrony can be considered as no-equilibrium phase transition and can be described in terms of order parameters. The emergence of order parameters can be theoretically explored based on the synergetic theory, central manifold theorem and statistical physics. In this paper, we discuss the order-parameter theory of synchronization in terms of statistical physics and set up the dynamical equations of order parameters. We also apply this theory to studying the nonlinear dynamics and bifurcation of order parameters in several typical coupled oscillator systems.

Keywords:

作者及机构信息

1.
华侨大学系统科学研究所, 厦门　361021

2.
华侨大学信息科学与工程学院, 厦门　361021

3.
北京邮电大学理学院, 北京　100876

通信作者: 郑志刚, zgzheng@hqu.edu.cn ; 徐灿, xucan@hqu.edu.cn

基金项目: 国家级-复杂系统群体行为的序参量动力学与重构：理论及应用(11875135)

Authors and contacts

1.
Institute of Systems Science, Huaqiao University, Xiamen 361021, China

2.
College of Information Science and Engineering, Huaqiao University, Xiamen 361201, China

3.
School of Science, Beijing University of Posts and Telecommunications, Beijing 100876, China

Corresponding author: Zheng Zhi-Gang, zgzheng@hqu.edu.cn ; Xu Can, xucan@hqu.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Glass L, Mackay M C 1988 From Clocks to Chaos: The Rhythms of Life (Princeton: Princeton University Press) p10
[2]	Mikhailov A S, Calenbuhr V 2002 From Cells to Societies: Models of Complex Coherent Action (Berlin: Springer-Verlag) pp127−154
[3]	郑志刚 2004 耦合非线性系统的时空动力学与合作行为 (北京: 高等教育出版社)第53−85页 Zheng Z G 2004 Spatiotemporal Dynamics and Cooperative Behaviors in Coupled Nonlinear Systems (Beijing: Higher Education Press) pp53−85 (in Chinese)
[4]	Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization, A Universal Concept in Nonlinear Sciences (New York: Cambridge University Press) pp1−24
[5]	Strogatz S 2003 Sync: The Emerging Science of Spontaneous Order (New York: Hyperion) pp103−152
[6]	Wiener N 1965 Cybernetics or Control and Communication in the Animal and the Machine (Cambridge: MIT Press) p65
[7]	Winfree A T 1967 J. Theor. Biol. 16 15 Google Scholar
[8]	Kuramoto Y 1975 Self-entrainment of a Population of Coupled Non-linear Oscillators, in: International Symposium on Mathematical Problems in Theoretical Physics (Berlin: Springer) pp420−428
[9]	Kuramoto Y 1984 Chemical Oscillations, Waves and Turbulence (Berlin: Springer-Verlag) pp60−66
[10]	Kuramoto Y, Nishikawa I 1987 J. Stat. Phys. 49 569 Google Scholar
[11]	Acebrón J A, Bonilla L L, Vicente C J P, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137 Google Scholar
[12]	Bocaletti S, Kurths J, Osipov G, Valladares D, Zhou C 2002 Phys. Rep. 336 1
[13]	Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou C 2008 Phys. Rep. 469 93 Google Scholar
[14]	Rodrigues F A, Peron T K DM, Ji P, Kurths J 2016 Phys. Rep. 610 1 Google Scholar
[15]	Osipov G V, Kurths J, Zhou C S 2007 Synchronization in Oscillatory Networks, Springer Series in Synergetics (Berlin: Springer-Verlag) pp3−10
[16]	Balanov A, Janson N, Postnov D, Sosnovtseva O 2009 Synchronization: From Simle to Complex (Berlin: Springer-Verlag) p21
[17]	Zheng Z G 2011 Synchronization of Coupled Phase Oscillators (New York: Nova Science Publishing House) pp293−327
[18]	Komarov M, Pikovsky A 2014 Physica D 289 18 Google Scholar
[19]	Komarov M, Pikovsky A 2013 Phys. Rev. Lett. 111 204101 Google Scholar
[20]	Hong H, Choi M Y, Kim B J 2002 Phys. Rev. E 65 026139 Google Scholar
[21]	Moreno Y, Pacheco A F 2004 Europhys. Lett. 68 603 Google Scholar
[22]	Gomez-Gardenes J, Gomez S, Arenas A, et al. 2011 Phys. Rev. Lett 106 12870
[23]	Peron T K D, Rodrigues F A 2012 Phys. Rev. E 86 056108 Google Scholar
[24]	Peron T, de Resende B M F, Mata A S, Rodrigues F A, Moreno Y 2019 Phys. Rev. E 100 042302
[25]	Xu C, Gao J, Sun Y T, Huang X, Zheng Z G 2015 Sci. Rep. 5 12039 Google Scholar
[26]	O’Keeffe K P, Krapivsky P L, Strogatz S H 2015 Phys. Rev. Lett. 115 064101 Google Scholar
[27]	Bonilla L L, Perez Vicente C J, Rubi J M 1993 J. Stat. Phys. 70 921 Google Scholar
[28]	Hong H, Strogatz S H 2011 Phys. Rev. Lett. 106 054102 Google Scholar
[29]	Hong H, Strogatz S H 2012 Phys. Rev. E 85 056210 Google Scholar
[30]	Tanaka H, Lichtenberg A J, Oishi S 1997 Phys. Rev. Lett. 78 2104 Google Scholar
[31]	Gao J, Efstathiou K 2018 Phys. Rev. E 98 042201 Google Scholar
[32]	Omata S, Yamaguchi Y, Shimizu H 1988 Physica D 31 397 Google Scholar
[33]	Zheng Z G 2001 Chin. Phys. 10 703 Google Scholar
[34]	Zhang T X, Zheng Z G 2009 Phys. B 18 1674
[35]	Omel’chenko E, Wolfrum M 2012 Phys. Rev. Lett. 109 164101 Google Scholar
[36]	Yeung M K S, Strogatz S H 1999 Phys. Rev. Lett. 82 648 Google Scholar
[37]	Childs L M, Strogatz S H 2008 Chaos 18 043128 Google Scholar
[38]	Petkoski S, Stefanovska A 2012 Phys. Rev. E 86 046212 Google Scholar
[39]	Cohen A H, Holmes P J, Rand R H 1982 J. Math. Biol. 13 345 Google Scholar
[40]	Ermentrout G B, Kopell N 1984 SIAM J. Math. Anal. 15 215 Google Scholar
[41]	Strogatz S H, Mirollo R E 1988 Physica D 31 143 Google Scholar
[42]	Zheng Z G, Hu G, Hu B 1998 Phys. Rev. Lett. 81 5318 Google Scholar
[43]	Zheng Z G, Hu B, Hu G 2000 Phys. Rev. E 62 402
[44]	Hu B, Zheng Z G 2000 Int. J. Bif. & Chaos 10 2399
[45]	Pikovsky A, Rosenblum M 2015 Chaos 25 097616 Google Scholar
[46]	Watanabe S, Strogatz S H 1994 Phys. Rev. Lett. 70 2391
[47]	Ott E, Antonsen T M 2008 Chaos 18 037113 Google Scholar
[48]	Ott E, Antonsen T M 2009 Chaos 19 023117 Google Scholar
[49]	Marvel S A, Strogatz S H 2009 Chaos 19 013132 Google Scholar
[50]	Marvel S A, Mirollo R E, Strogatz S H 2009 Chaos 19 043104 Google Scholar
[51]	郑志刚 2019 复杂系统的涌现动力学: 从同步到集体输运 (北京: 科学出版社) 第95−176页 Zheng Z G 2019 Emergence Dynamics in Complex Systems: From Synchronization to Collective Transport (Beijing: Science Press) pp95−176 (in Chinese)
[52]	Nicolis G, Prigogine I 1989 Exploring Complexity: An Introduction (New York: W. H. Freeman) pp21−25
[53]	Prigogine I, Nicolis G 1977 Self-Organization in Non-Equilibrium Systems (New Jersey: Wiley) pp63−222
[54]	Haken H 1983 Synergetics: An Introduction (3rd Ed.) (Berlin: Springer-Verlag) pp191−224
[55]	Haken H 1983 Advanced Synergetics (Berlin: Springer Verlag) pp187−221
[56]	Gao J, Xu C, Sun Y T, Zheng Z G 2016 Sci. Rep. 6 30184 Google Scholar
[57]	Tristan N 1997 Visual Complex Analysis (Oxford: Clarendon Press) p1
[58]	Xu C, Xiang H, Gao J, Zheng Z G 2016 Sci. Rep. 6 31133 Google Scholar
[59]	Yao N, Zheng Z G 2016 Int. J. Mod. Phys. B 30 7 1630002
[60]	郑志刚, 翟云 2020 中国科学: 物理学力学天文学 50 010505 Google Scholar Zheng Z G, Zhai Y 2020 Sci. Sin.-Phys. Mech. Astron. 50 010505 Google Scholar
[61]	刘宗华 2018 混沌动力学基础及其在大脑功能方面的应用 (北京: 科学出版社) 第234−256页 Liu Z H 2018 Chaotic Dynamics Foundation and Its Applications in Brain functions (Beijing: Science Press) pp234−256 (in Chinese)
[62]	Abrams D M, Strogatz S H 2004 Phys. Rev. Lett. 93 174102 Google Scholar
[63]	Omel'chenko E, Maistrenko Y L, Tass P A 2008 Phys. Rev. Lett. 100 044105 Google Scholar
[64]	Sethia G C, Sen A 2014 Phys. Rev. Lett. 112 144101 Google Scholar
[65]	Zakharova A, Kapeller M, Schol E 2014 Phys. Rev. Lett. 112 154101 Google Scholar
[66]	Omelchenko I, Maistrenko Y, Hovel P, et al. 2011 Phys. Rev. Lett 106 234102 Google Scholar
[67]	Gu C, St-Yves G, Davidsen J 2013 Phys. Rev. Lett. 111 134101 Google Scholar
[68]	Hagerstrom A M, Murphy T E, Roy R, et al. 2012 Nat. Phys 8 658 Google Scholar
[69]	Tinsley M R, Nkomo S, Showalter K 2012 Nat. Phys. 8 662 Google Scholar
[70]	Abrams D M, Strogatz S H 2006 Int. J. Bif. & Chaos 16 21
[71]	Laing C R 2009 Physica D 238 1569 Google Scholar
[72]	Daido H 1992 Prog. Theor. Phys. 88 1213 Google Scholar
[73]	Pikovsky A, Rosenblum M 2008 Phys. Rev. Lett. 101 264103 Google Scholar
[74]	Gong C C 2019 arXiv 1909.07718
[75]	Komarov M, Pikovsky A 2015 Phys. Rev. E 92 020901 Google Scholar
[76]	Skardal P S, Arenas A 2019 Phys. Rev. Lett. 122 248301 Google Scholar
[77]	Skardal P, Ott E, Restrepo J G 2011 Phys. Rev. E 84 036208 Google Scholar
[78]	Yuan D, Cui H, Tian J, Xiao Y, Zhang Y 2016 Commun. Nonlinear Sci. Numer. Simul. 38 23 Google Scholar
[79]	Wang H, Han W, Yang J 2017 Phys. Rev. E 96 022202 Google Scholar
[80]	Czolczynski K, Perlikowski P, Stefanski A, Kapitaniak T 2013 Commun. Nonlinear. Sci. Numer. Simul. 18 386 Google Scholar
[81]	Goldobin E, Koelle D, Kleiner R, Kleiner R G 2011 Phys. Rev. Lett. 107 227001 Google Scholar
[82]	Goldobin E, Kleiner R, Koelle D, Mints R G 2013 Phys. Rev. Lett. 111 057004 Google Scholar
[83]	Kiss I Z, Zhai Y, Hudson J L 2005 Phys. Rev. Lett. 94 248301 Google Scholar
[84]	Huang X H, Zheng Z G, Hu G, Wu S, Rasch M J 2015 New J. Phys. 17 035006 Google Scholar
[85]	Zhang Z Y, Zheng Z G, Niu H J, Mi Y Y, Wu S, Hu G 2015 Phys. Rev. E 91 012814 Google Scholar
[86]	Chen Y, Wang S H, Zheng Z G, Zhang Z Y, Hu G 2016 EPL 113 18005 Google Scholar

施引文献

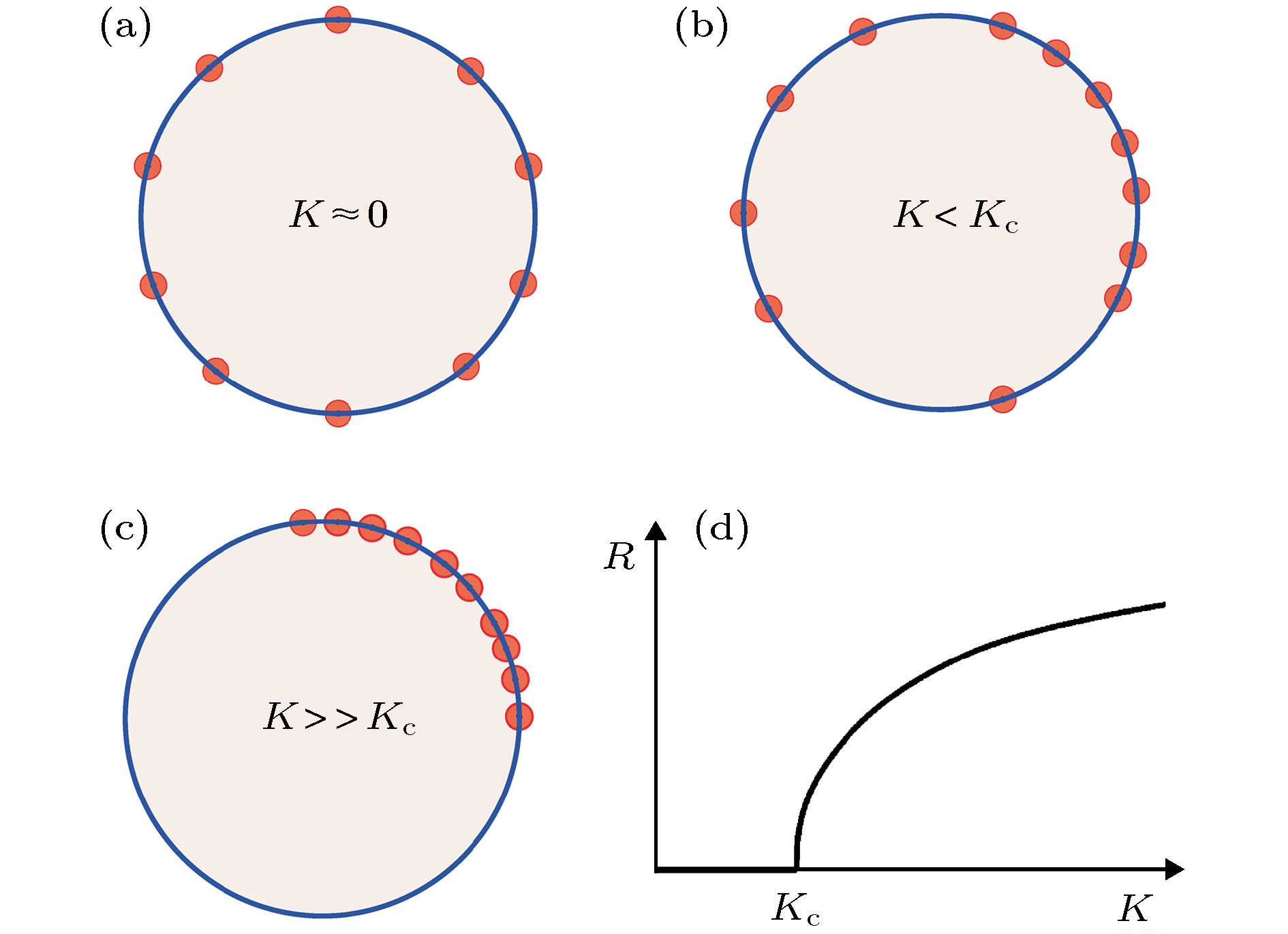
图 1 耦合振子同步示意图　(a) 在耦合强度很弱时, 大量振子不同步, 任一时刻相位均匀分布于0−2π之间; (b)随着耦合强度的增加, 越来越多的振子会同步, 振子不再均匀分布; (c) 在很强的耦合下, 振子相位会靠得很近, 形成整体的同步大集团; (d) 序参量随耦合强度的变化

Fig. 1. A schematic diagram of synchronization of coupled oscillators: (a) Most of the oscillators are asynchronous and evenly distributed along the circle; (b) with increasing the coupling, more and more oscillators are synchronized and are no longer evenly distributed; (c) under a strong coupling, oscillators form a single synchronous cluster, and the phases of oscillators are close to each other; (d) dependence of the order parameter on the coupling strength

下载: 全尺寸图片幻灯片

图 2 序参量α相空间的Poincare截面落点分布, 可以看到闭合环面和混沌散点

Fig. 2. The Poincare section of the order parameter α in phase space, where one can find the closed tori and chaotic scattered points.

下载: 全尺寸图片幻灯片

map

[1]	Glass L, Mackay M C 1988 From Clocks to Chaos: The Rhythms of Life (Princeton: Princeton University Press) p10
[2]	Mikhailov A S, Calenbuhr V 2002 From Cells to Societies: Models of Complex Coherent Action (Berlin: Springer-Verlag) pp127−154
[3]	郑志刚 2004 耦合非线性系统的时空动力学与合作行为 (北京: 高等教育出版社)第53−85页 Zheng Z G 2004 Spatiotemporal Dynamics and Cooperative Behaviors in Coupled Nonlinear Systems (Beijing: Higher Education Press) pp53−85 (in Chinese)
[4]	Pikovsky A, Rosenblum M, Kurths J 2001 Synchronization, A Universal Concept in Nonlinear Sciences (New York: Cambridge University Press) pp1−24
[5]	Strogatz S 2003 Sync: The Emerging Science of Spontaneous Order (New York: Hyperion) pp103−152
[6]	Wiener N 1965 Cybernetics or Control and Communication in the Animal and the Machine (Cambridge: MIT Press) p65
[7]	Winfree A T 1967 J. Theor. Biol. 16 15 Google Scholar
[8]	Kuramoto Y 1975 Self-entrainment of a Population of Coupled Non-linear Oscillators, in: International Symposium on Mathematical Problems in Theoretical Physics (Berlin: Springer) pp420−428
[9]	Kuramoto Y 1984 Chemical Oscillations, Waves and Turbulence (Berlin: Springer-Verlag) pp60−66
[10]	Kuramoto Y, Nishikawa I 1987 J. Stat. Phys. 49 569 Google Scholar
[11]	Acebrón J A, Bonilla L L, Vicente C J P, Ritort F, Spigler R 2005 Rev. Mod. Phys. 77 137 Google Scholar
[12]	Bocaletti S, Kurths J, Osipov G, Valladares D, Zhou C 2002 Phys. Rep. 336 1
[13]	Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou C 2008 Phys. Rep. 469 93 Google Scholar
[14]	Rodrigues F A, Peron T K DM, Ji P, Kurths J 2016 Phys. Rep. 610 1 Google Scholar
[15]	Osipov G V, Kurths J, Zhou C S 2007 Synchronization in Oscillatory Networks, Springer Series in Synergetics (Berlin: Springer-Verlag) pp3−10
[16]	Balanov A, Janson N, Postnov D, Sosnovtseva O 2009 Synchronization: From Simle to Complex (Berlin: Springer-Verlag) p21
[17]	Zheng Z G 2011 Synchronization of Coupled Phase Oscillators (New York: Nova Science Publishing House) pp293−327
[18]	Komarov M, Pikovsky A 2014 Physica D 289 18 Google Scholar
[19]	Komarov M, Pikovsky A 2013 Phys. Rev. Lett. 111 204101 Google Scholar
[20]	Hong H, Choi M Y, Kim B J 2002 Phys. Rev. E 65 026139 Google Scholar
[21]	Moreno Y, Pacheco A F 2004 Europhys. Lett. 68 603 Google Scholar
[22]	Gomez-Gardenes J, Gomez S, Arenas A, et al. 2011 Phys. Rev. Lett 106 12870
[23]	Peron T K D, Rodrigues F A 2012 Phys. Rev. E 86 056108 Google Scholar
[24]	Peron T, de Resende B M F, Mata A S, Rodrigues F A, Moreno Y 2019 Phys. Rev. E 100 042302
[25]	Xu C, Gao J, Sun Y T, Huang X, Zheng Z G 2015 Sci. Rep. 5 12039 Google Scholar
[26]	O’Keeffe K P, Krapivsky P L, Strogatz S H 2015 Phys. Rev. Lett. 115 064101 Google Scholar
[27]	Bonilla L L, Perez Vicente C J, Rubi J M 1993 J. Stat. Phys. 70 921 Google Scholar
[28]	Hong H, Strogatz S H 2011 Phys. Rev. Lett. 106 054102 Google Scholar
[29]	Hong H, Strogatz S H 2012 Phys. Rev. E 85 056210 Google Scholar
[30]	Tanaka H, Lichtenberg A J, Oishi S 1997 Phys. Rev. Lett. 78 2104 Google Scholar
[31]	Gao J, Efstathiou K 2018 Phys. Rev. E 98 042201 Google Scholar
[32]	Omata S, Yamaguchi Y, Shimizu H 1988 Physica D 31 397 Google Scholar
[33]	Zheng Z G 2001 Chin. Phys. 10 703 Google Scholar
[34]	Zhang T X, Zheng Z G 2009 Phys. B 18 1674
[35]	Omel’chenko E, Wolfrum M 2012 Phys. Rev. Lett. 109 164101 Google Scholar
[36]	Yeung M K S, Strogatz S H 1999 Phys. Rev. Lett. 82 648 Google Scholar
[37]	Childs L M, Strogatz S H 2008 Chaos 18 043128 Google Scholar
[38]	Petkoski S, Stefanovska A 2012 Phys. Rev. E 86 046212 Google Scholar
[39]	Cohen A H, Holmes P J, Rand R H 1982 J. Math. Biol. 13 345 Google Scholar
[40]	Ermentrout G B, Kopell N 1984 SIAM J. Math. Anal. 15 215 Google Scholar
[41]	Strogatz S H, Mirollo R E 1988 Physica D 31 143 Google Scholar
[42]	Zheng Z G, Hu G, Hu B 1998 Phys. Rev. Lett. 81 5318 Google Scholar
[43]	Zheng Z G, Hu B, Hu G 2000 Phys. Rev. E 62 402
[44]	Hu B, Zheng Z G 2000 Int. J. Bif. & Chaos 10 2399
[45]	Pikovsky A, Rosenblum M 2015 Chaos 25 097616 Google Scholar
[46]	Watanabe S, Strogatz S H 1994 Phys. Rev. Lett. 70 2391
[47]	Ott E, Antonsen T M 2008 Chaos 18 037113 Google Scholar
[48]	Ott E, Antonsen T M 2009 Chaos 19 023117 Google Scholar
[49]	Marvel S A, Strogatz S H 2009 Chaos 19 013132 Google Scholar
[50]	Marvel S A, Mirollo R E, Strogatz S H 2009 Chaos 19 043104 Google Scholar
[51]	郑志刚 2019 复杂系统的涌现动力学: 从同步到集体输运 (北京: 科学出版社) 第95−176页 Zheng Z G 2019 Emergence Dynamics in Complex Systems: From Synchronization to Collective Transport (Beijing: Science Press) pp95−176 (in Chinese)
[52]	Nicolis G, Prigogine I 1989 Exploring Complexity: An Introduction (New York: W. H. Freeman) pp21−25
[53]	Prigogine I, Nicolis G 1977 Self-Organization in Non-Equilibrium Systems (New Jersey: Wiley) pp63−222
[54]	Haken H 1983 Synergetics: An Introduction (3rd Ed.) (Berlin: Springer-Verlag) pp191−224
[55]	Haken H 1983 Advanced Synergetics (Berlin: Springer Verlag) pp187−221
[56]	Gao J, Xu C, Sun Y T, Zheng Z G 2016 Sci. Rep. 6 30184 Google Scholar
[57]	Tristan N 1997 Visual Complex Analysis (Oxford: Clarendon Press) p1
[58]	Xu C, Xiang H, Gao J, Zheng Z G 2016 Sci. Rep. 6 31133 Google Scholar
[59]	Yao N, Zheng Z G 2016 Int. J. Mod. Phys. B 30 7 1630002
[60]	郑志刚, 翟云 2020 中国科学: 物理学力学天文学 50 010505 Google Scholar Zheng Z G, Zhai Y 2020 Sci. Sin.-Phys. Mech. Astron. 50 010505 Google Scholar
[61]	刘宗华 2018 混沌动力学基础及其在大脑功能方面的应用 (北京: 科学出版社) 第234−256页 Liu Z H 2018 Chaotic Dynamics Foundation and Its Applications in Brain functions (Beijing: Science Press) pp234−256 (in Chinese)
[62]	Abrams D M, Strogatz S H 2004 Phys. Rev. Lett. 93 174102 Google Scholar
[63]	Omel'chenko E, Maistrenko Y L, Tass P A 2008 Phys. Rev. Lett. 100 044105 Google Scholar
[64]	Sethia G C, Sen A 2014 Phys. Rev. Lett. 112 144101 Google Scholar
[65]	Zakharova A, Kapeller M, Schol E 2014 Phys. Rev. Lett. 112 154101 Google Scholar
[66]	Omelchenko I, Maistrenko Y, Hovel P, et al. 2011 Phys. Rev. Lett 106 234102 Google Scholar
[67]	Gu C, St-Yves G, Davidsen J 2013 Phys. Rev. Lett. 111 134101 Google Scholar
[68]	Hagerstrom A M, Murphy T E, Roy R, et al. 2012 Nat. Phys 8 658 Google Scholar
[69]	Tinsley M R, Nkomo S, Showalter K 2012 Nat. Phys. 8 662 Google Scholar
[70]	Abrams D M, Strogatz S H 2006 Int. J. Bif. & Chaos 16 21
[71]	Laing C R 2009 Physica D 238 1569 Google Scholar
[72]	Daido H 1992 Prog. Theor. Phys. 88 1213 Google Scholar
[73]	Pikovsky A, Rosenblum M 2008 Phys. Rev. Lett. 101 264103 Google Scholar
[74]	Gong C C 2019 arXiv 1909.07718
[75]	Komarov M, Pikovsky A 2015 Phys. Rev. E 92 020901 Google Scholar
[76]	Skardal P S, Arenas A 2019 Phys. Rev. Lett. 122 248301 Google Scholar
[77]	Skardal P, Ott E, Restrepo J G 2011 Phys. Rev. E 84 036208 Google Scholar
[78]	Yuan D, Cui H, Tian J, Xiao Y, Zhang Y 2016 Commun. Nonlinear Sci. Numer. Simul. 38 23 Google Scholar
[79]	Wang H, Han W, Yang J 2017 Phys. Rev. E 96 022202 Google Scholar
[80]	Czolczynski K, Perlikowski P, Stefanski A, Kapitaniak T 2013 Commun. Nonlinear. Sci. Numer. Simul. 18 386 Google Scholar
[81]	Goldobin E, Koelle D, Kleiner R, Kleiner R G 2011 Phys. Rev. Lett. 107 227001 Google Scholar
[82]	Goldobin E, Kleiner R, Koelle D, Mints R G 2013 Phys. Rev. Lett. 111 057004 Google Scholar
[83]	Kiss I Z, Zhai Y, Hudson J L 2005 Phys. Rev. Lett. 94 248301 Google Scholar
[84]	Huang X H, Zheng Z G, Hu G, Wu S, Rasch M J 2015 New J. Phys. 17 035006 Google Scholar
[85]	Zhang Z Y, Zheng Z G, Niu H J, Mi Y Y, Wu S, Hu G 2015 Phys. Rev. E 91 012814 Google Scholar
[86]	Chen Y, Wang S H, Zheng Z G, Zhang Z Y, Hu G 2016 EPL 113 18005 Google Scholar

[1]	丁学利, 古华光, 贾冰, 李玉叶. 抑制性自突触诱发耦合Morris-Lecar神经元电活动的超前同步. , 2021, 70(21): 218701. doi: 10.7498/aps.70.20210912
[2]	杨永霞, 李玉叶, 古华光. Pre-Bötzinger复合体的从簇到峰放电的同步转迁及分岔机制. , 2020, 69(4): 040501. doi: 10.7498/aps.69.20191509
[3]	向俊杰, 毕闯, 向勇, 张千, 王京梅. 峰值电流模式控制同步开关Z源变换器的动力学研究. , 2014, 63(12): 120507. doi: 10.7498/aps.63.120507
[4]	刘洪臣, 王云, 苏振霞. 单相三电平H桥逆变器分岔现象的研究. , 2013, 62(24): 240506. doi: 10.7498/aps.62.240506
[5]	黄晨, 陈龙, 毕勤胜, 江浩斌. 机动车协商模型与分岔特性研究. , 2013, 62(21): 210507. doi: 10.7498/aps.62.210507
[6]	王付霞, 谢勇. "Hopf/homoclinic"簇放电和"SubHopf/homoclinic"簇放电之间的同步. , 2013, 62(2): 020509. doi: 10.7498/aps.62.020509
[7]	李海滨, 王博华, 张志强, 刘爽, 李延树. 一类非线性相对转动系统的组合共振分岔与混沌. , 2012, 61(9): 094501. doi: 10.7498/aps.61.094501
[8]	李群宏, 闫玉龙, 杨丹. 耦合电路系统的分岔研究. , 2012, 61(20): 200505. doi: 10.7498/aps.61.200505
[9]	吕翎, 李钢, 徐文, 吕娜, 范鑫. 复Ginzburg-Landau方程时空混沌的网络同步与参量辨识. , 2012, 61(6): 060507. doi: 10.7498/aps.61.060507
[10]	吴淑花, 孙毅, 郝建红, 许海波. 耦合发电机系统的分岔和双参数特性. , 2011, 60(1): 010507. doi: 10.7498/aps.60.010507
[11]	张荣, 徐振源, 杨永清. 通过同步实现"有序+有序=混沌"的例子. , 2011, 60(1): 010515. doi: 10.7498/aps.60.010515
[12]	吕翎, 李钢, 张檬, 李雨珊, 韦琳玲, 于淼. 全局耦合网络的参量辨识与时空混沌同步. , 2011, 60(9): 090505. doi: 10.7498/aps.60.090505
[13]	何学军, 张良欣, 任爱娣. 横向补给系统高架索的稳定性与分岔研究. , 2010, 59(5): 3088-3092. doi: 10.7498/aps.59.3088
[14]	陈章耀, 毕勤胜. Jerk系统耦合的分岔和混沌行为. , 2010, 59(11): 7669-7678. doi: 10.7498/aps.59.7669
[15]	包伯成, 康祝圣, 许建平, 胡文. 含指数项广义平方映射的分岔和吸引子. , 2009, 58(3): 1420-1431. doi: 10.7498/aps.58.1420
[16]	张维, 周淑华, 任勇, 山秀明. Turbo译码算法的分岔与控制. , 2006, 55(2): 622-627. doi: 10.7498/aps.55.622
[17]	郭四玲, 韦艳芳, 薛郁. 元胞自动机交通流模型的相变特性研究. , 2006, 55(7): 3336-3342. doi: 10.7498/aps.55.3336
[18]	李　明, 马西奎, 戴　栋, 张　浩. 基于符号序列描述的一类分段光滑系统中分岔现象与混沌分析. , 2005, 54(3): 1084-1091. doi: 10.7498/aps.54.1084
[19]	宋晓红, 林圣路. 外电场中Li原子回归谱的分岔效应. , 2003, 52(7): 1611-1616. doi: 10.7498/aps.52.1611
[20]	杨世平, 牛海燕, 田钢, 袁国勇, 张闪. 用驱动参量法实现混沌系统的同步. , 2001, 50(4): 619-623. doi: 10.7498/aps.50.619

计量

文章访问数: 11975
PDF下载量: 457
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

耦合相振子系统同步的序参量理论