-
Sapphires (Al2O3) is an important ceramic material with extensive applications in high-pressure technology and geoscience. For instance, it is often used as a window material in shock-wave experiments. Consequently, understanding the behavior of its transparency change under shock compression is crucial for correctly interpreting the experimental data. Sapphire has excellent transparency at ambient conditions, but its transparency is reduced under shock loading. This shock-induced optical extinction phenomenon in Al2O3 has been studied experimentally and theoretically a lot at present, but the knowledge on the crystal-orientation effects of the extinction is still insufficient. the experimental investigations at low-pressure region (within 86 GPa) have indicated that the shock-induced extinction in Al2O3 is related to its crystal orientation, but it is not clear whether the correlation also exists at high-pressure region (~131–255 GPa). Here, to investigate this question, we have performed first principles calculations of the optical absorption properties of a-, c-, d-, r-, n-, s-, g- and m-oriented Al2O3 crystals without and with
$V_{\rm O}^{ + 2}$ (the +2 charged O vacancy) defects at the pressure range of 131–255 GPa. It is found that: 1) there are obvious crystal-orientation effects of the extinction in shocked Al2O3 at high-pressure region, and they strengthen with increasing pressure; 2) shock-induced$V_{\rm O}^{ + 2}$ defects could play an important role in determining these crystal-orientation effects, but the influences of pressure and temperature factors on them are relatively weak. A further analysis shows that, at the wavelength range adopted in shock experiments, the extinction of a-orientation is the weakest (the best transparency), the extinction of c-orientation is the strongest (the worst transparency), and the extinction of s-orientation is between them; at the same time, the extinction of m-orientation is similar to that of a-orientation, the extinction of r-, n- and d-orientations is close to that of c-orientation, and the extinction of g-orientation is weaker than that of s-orientation. In view of this, we suggest that the a- or m-oriented Al2O3 is chosen as an optical window in shock-wave experiments of the high-pressure region. Our predictions could be not only helpful to understand further the optical properties of Al2O3 at extreme conditions, but also important for future experimental study.-
Keywords:
- sapphires /
- high pressure /
- shock-induced optical extinction /
- crystal-orientation effects /
- first-principles calculations
[1] Xu Y S, McCammon C, Poe B T 1998 Science 282 922
Google Scholar
[2] 周显明, 汪小松, 李赛男, 李俊, 李加波, 经福谦 2007 56 4965
Google Scholar
Zhou X M, Wang X S, Li S N, Li J, Li J B, Jing F Q 2007 Acta Phys. Sin. 56 4965
Google Scholar
[3] Oganov A R, Ono S 2005 Proc. Natl. Acad. Sci. USA 102 10828
Google Scholar
[4] Ono S, Oganov A R, Koyama T, Shimizu H 2006 Earth Planet. Sci. Lett. 246 326
Google Scholar
[5] Lin J F, Degtyareva O, Prewitt C T, Dera P, Sata N, Gregoryanz E, Mao H K, Hemley R J 2004 Nat. Mater. 3 389
Google Scholar
[6] 操秀霞 2011 硕士学位论文 (成都: 四川大学)
Cao X X 2011 M. S. Thesis (Chengdu: Sichuan University) (in Chinese)
[7] Zhang D Y, Liu F S, Hao G Y, Sun Y H 2007 Chin. Phys. Lett. 24 2341
Google Scholar
[8] 唐士惠, 操秀霞, 何林, 祝文军 2016 65 202
Tang S H, Cao X X, He L, Zhu W J 2016 Acta Phys. Sin. 65 202
[9] He L, Tang M J, Fang Y, Jing F Q 2008 Europhys. Lett. 83 39001
Google Scholar
[10] 张岱宇, 郝高宇, 张明建, 刘福生 2007 人工晶体学报 36 531
Google Scholar
Zhang D Y, Hao G Y, Zhang M J, Liu F S 2007 Journal of Synthetic Crystals 36 531
Google Scholar
[11] Kanel G I, Nellis W J, Savinykh A S, Razorenov S V, Rajendran A M 2009 J. Appl. Phys. 106 043524
Google Scholar
[12] Fat’yanov O V, Webb R L, Gupta Y M 2005 J. Appl. Phys. 97 123529
Google Scholar
[13] Hare D E, Webb D J, Lee S H, Holmes N C 2002 Optical Extinction of Sapphire Shock‐Loaded to 250−260 GPa. In Shock Compression of Condensed Matter-2001: 12th APS Topical Conference Atlanta, USA, June 24−29, 2001 p1231
[14] Kwiatkowski C S, Gupta Y M 2000 Optical Measurements to Probe Inelastic Deformation in Shocked Brittle Materials. Shock Compression of Condensed Matter-1999 (New York: Elsevier Science Publishers) pp641−644
[15] Umemoto K, Wentzcovitch R M 2008 Proc. Natl. Acad. Sci. USA 105 6526
Google Scholar
[16] He L, Tang M J, Yin J, Zhou X M, Zhu W J, Liu F S, He D W 2012 Physica B 407 694
Google Scholar
[17] He L, Tang M J, Zeng M F, Zhou X M, Zhu W J, Liu F S 2013 Physica B 410 137
Google Scholar
[18] 何旭, 何林, 唐明杰, 徐明 2011 60 026102
Google Scholar
He X, He L, Tang M J, Xu M 2011 Acta Phys. Sin. 60 026102
Google Scholar
[19] Cao X X, Wang Y, Li X H, Xu L, Liu L X, Yu Y, Qin R, Zhu W J, Tang S H, He L, Meng C M, Zhang B T, Peng X S 2017 J. Appl. Phys. 121 115903
Google Scholar
[20] Weir S T, Mitchell A C, Nellis W J 1996 J. Appl. Phys. 80 1522
Google Scholar
[21] Meyers M A 1994 Dynamic Behavior of Materials (New York: Wiley-IEEE) p413
[22] Hicks D G, Celliers P M, Collins G W, Eggert J H, Moon S J 2003 Phys. Rev. Lett. 91 035502
Google Scholar
[23] Liu Y, Oganov A R, Wang S, Zhu Q, Dong X, Kresse G 2015 Sci. Rep. 5 9518
Google Scholar
[24] Marsh S P 1980 LASL Shock Hugoniot Data (Berkeley: University of California Press)
[25] Liu H, Tse J S, Nellis W J 2015 Sci. Rep. 5 12823
Google Scholar
[26] Matsunaga K, Tanaka T, Yamamoto T, Lkuhara Y 2003 Phys. Rev. B 68 085110
Google Scholar
[27] Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. : Condens. Matter 14 2717
Google Scholar
[28] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133
Google Scholar
[29] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[30] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[31] Fischer T H, Almlof J 1992 J. Phys. Chem. 96 9768
Google Scholar
[32] 贾婉丽, 周淼, 王馨梅, 纪卫莉 2018 67 107102
Google Scholar
Jia W L, Zhou M, Wang X M, Ji W L 2018 Acta Phys. Sin. 67 107102
Google Scholar
[33] Brown G F, Wu J Q 2009 Laser Photon. Rev. 3 394
Google Scholar
[34] Ching W Y, Xu Y N 1994 J. Am. Ceram. Soc. 77 404
Google Scholar
[35] Wu J, Walukiewicz W, Shan W, Yu K M, Ager Ⅲ J W, Li S X, Haller E E, Lu H, Schaff W J 2003 J. Appl. Phys. 94 4457
Google Scholar
[36] French R H 1990 J. Am. Ceram. Soc. 73 477
Google Scholar
[37] Holm B, Ahuja R, Yourdshahyan Y, Johansson B, Lundqvist B I 1999 Phys. Rev. B 59 12777
Google Scholar
-
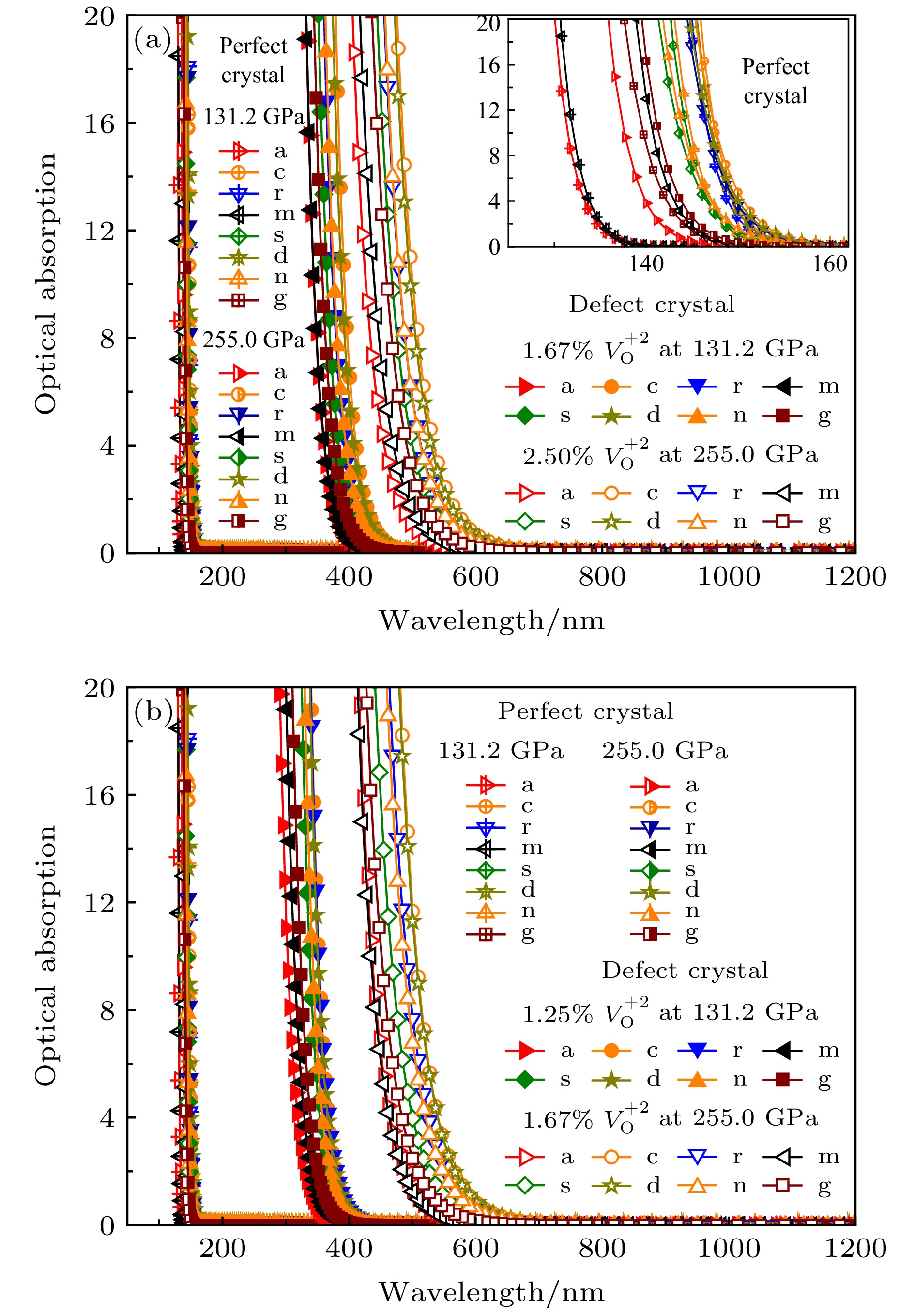
图 1 八种晶向 CalrO3-Al2O3的吸收光谱随冲击压力变化的规律(a, c, d, r, n, s, g 和 m 分别表示 a, c, d, r, n, s, g 和 m 晶向, 计算数据已做了冲击温度修正) (a) 在两个压力点分别采用较高缺陷浓度模型的计算数据(内嵌图为理想晶体数据的放大图); (b) 在两个压力点分别采用较低缺陷浓度模型的计算数据
Figure 1. Shock-pressure dependence of the optical absorption spectra for CalrO3-Al2O3 with eight crystallographic orientations (a, c, d, r, n, s, g and m indicate a, c, d, r, n, s, g and m orientations, respectively. The calculated data have been corrected by shock temperature): (a) Data calculated with higher defective concentration model at 131.2 GPa and 255 GPa (the inserted figure shows perfect-crystal data); (b) data calculated with lower defective concentration model at 131.2 GPa and 255 GPa.
图 2 八种晶向 CalrO3-Al2O3的理想晶体吸收光谱随压力变化的规律(a, c, d, r, n, s, g和m分别表示a, c, d, r, n, s, g和 m 晶向)
Figure 2. Pressure dependence of the optical absorption spectra for perfect CalrO3-Al2O3 with eight crystallographic orientations (a, c, d, r, n, s, g and m indicate a, c, d, r, n, s, g and m orientations, respectively).
图 3 冲击温度和空位点缺陷对八种晶向CalrO3-Al2O3高压吸收光谱的影响(a, c, d, r, n, s, g和m分别表示a, c, d, r, n, s, g和 m 晶向)
Figure 3. Effects of the shock temperature and vacancy point defect on the high-pressure optical absorption spectra for CalrO3-Al2O3 with eight crystallographic orientations (a, c, d, r, n, s, g and m indicate a, c, d, r, n, s, g and m orientations, respectively).
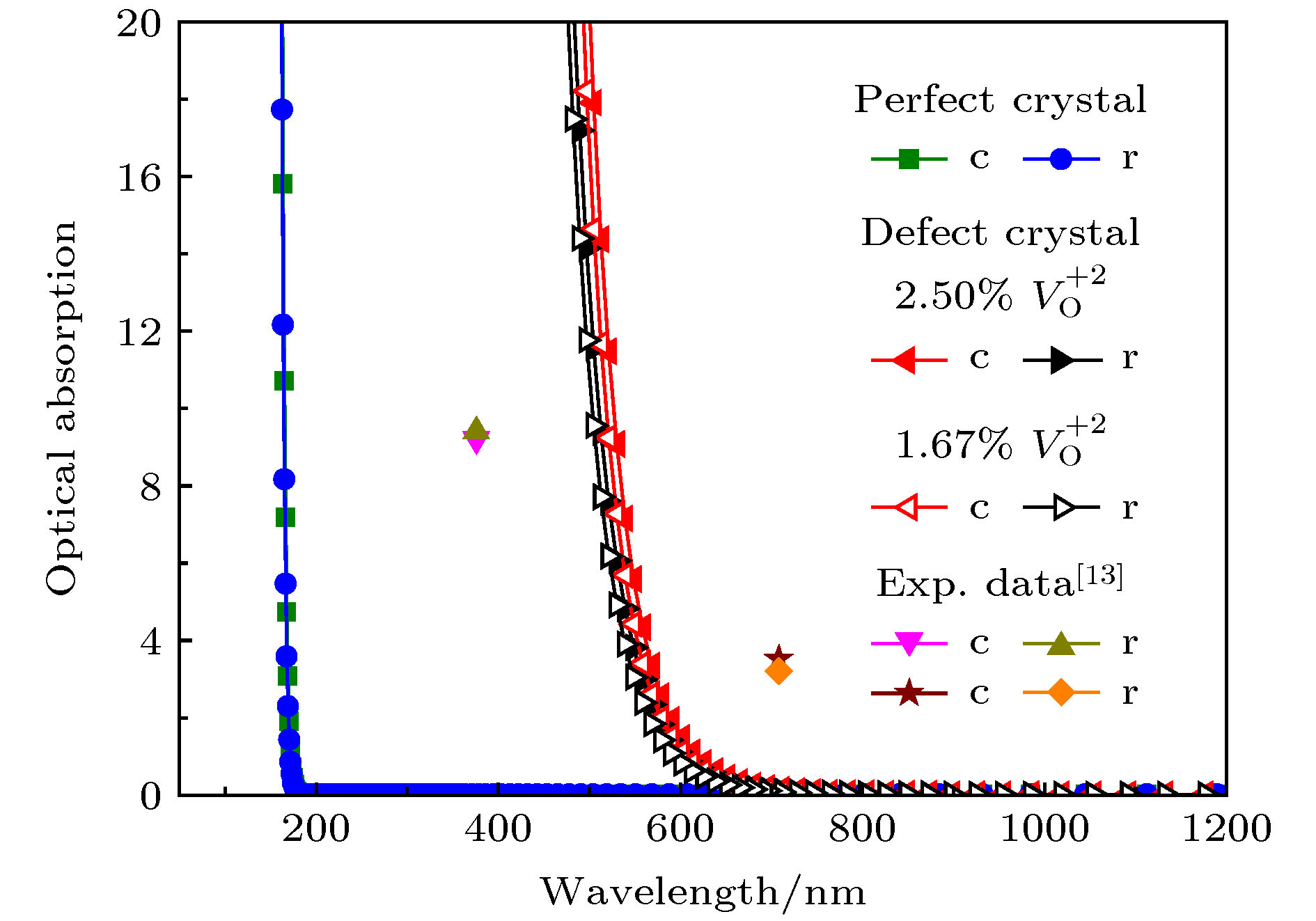
图 4 两个不同晶向 CalrO3-Al2O3在 255 GPa 处的冲击吸收光谱的计算数据和冲击消光系数的实测数据(c 和 r 分别表示 c 晶向和 r 晶向, 计算数据已做了冲击温度修正)
Figure 4. The calculated optical absorption spectra and the measured extinction coefficients for CalrO3-Al2O3 with two crystallographic orientations at shock pressure of 255 GPa (c and r indicate c and r orientations, respectively. The calculated data have been corrected by shock temperature).
-
[1] Xu Y S, McCammon C, Poe B T 1998 Science 282 922
Google Scholar
[2] 周显明, 汪小松, 李赛男, 李俊, 李加波, 经福谦 2007 56 4965
Google Scholar
Zhou X M, Wang X S, Li S N, Li J, Li J B, Jing F Q 2007 Acta Phys. Sin. 56 4965
Google Scholar
[3] Oganov A R, Ono S 2005 Proc. Natl. Acad. Sci. USA 102 10828
Google Scholar
[4] Ono S, Oganov A R, Koyama T, Shimizu H 2006 Earth Planet. Sci. Lett. 246 326
Google Scholar
[5] Lin J F, Degtyareva O, Prewitt C T, Dera P, Sata N, Gregoryanz E, Mao H K, Hemley R J 2004 Nat. Mater. 3 389
Google Scholar
[6] 操秀霞 2011 硕士学位论文 (成都: 四川大学)
Cao X X 2011 M. S. Thesis (Chengdu: Sichuan University) (in Chinese)
[7] Zhang D Y, Liu F S, Hao G Y, Sun Y H 2007 Chin. Phys. Lett. 24 2341
Google Scholar
[8] 唐士惠, 操秀霞, 何林, 祝文军 2016 65 202
Tang S H, Cao X X, He L, Zhu W J 2016 Acta Phys. Sin. 65 202
[9] He L, Tang M J, Fang Y, Jing F Q 2008 Europhys. Lett. 83 39001
Google Scholar
[10] 张岱宇, 郝高宇, 张明建, 刘福生 2007 人工晶体学报 36 531
Google Scholar
Zhang D Y, Hao G Y, Zhang M J, Liu F S 2007 Journal of Synthetic Crystals 36 531
Google Scholar
[11] Kanel G I, Nellis W J, Savinykh A S, Razorenov S V, Rajendran A M 2009 J. Appl. Phys. 106 043524
Google Scholar
[12] Fat’yanov O V, Webb R L, Gupta Y M 2005 J. Appl. Phys. 97 123529
Google Scholar
[13] Hare D E, Webb D J, Lee S H, Holmes N C 2002 Optical Extinction of Sapphire Shock‐Loaded to 250−260 GPa. In Shock Compression of Condensed Matter-2001: 12th APS Topical Conference Atlanta, USA, June 24−29, 2001 p1231
[14] Kwiatkowski C S, Gupta Y M 2000 Optical Measurements to Probe Inelastic Deformation in Shocked Brittle Materials. Shock Compression of Condensed Matter-1999 (New York: Elsevier Science Publishers) pp641−644
[15] Umemoto K, Wentzcovitch R M 2008 Proc. Natl. Acad. Sci. USA 105 6526
Google Scholar
[16] He L, Tang M J, Yin J, Zhou X M, Zhu W J, Liu F S, He D W 2012 Physica B 407 694
Google Scholar
[17] He L, Tang M J, Zeng M F, Zhou X M, Zhu W J, Liu F S 2013 Physica B 410 137
Google Scholar
[18] 何旭, 何林, 唐明杰, 徐明 2011 60 026102
Google Scholar
He X, He L, Tang M J, Xu M 2011 Acta Phys. Sin. 60 026102
Google Scholar
[19] Cao X X, Wang Y, Li X H, Xu L, Liu L X, Yu Y, Qin R, Zhu W J, Tang S H, He L, Meng C M, Zhang B T, Peng X S 2017 J. Appl. Phys. 121 115903
Google Scholar
[20] Weir S T, Mitchell A C, Nellis W J 1996 J. Appl. Phys. 80 1522
Google Scholar
[21] Meyers M A 1994 Dynamic Behavior of Materials (New York: Wiley-IEEE) p413
[22] Hicks D G, Celliers P M, Collins G W, Eggert J H, Moon S J 2003 Phys. Rev. Lett. 91 035502
Google Scholar
[23] Liu Y, Oganov A R, Wang S, Zhu Q, Dong X, Kresse G 2015 Sci. Rep. 5 9518
Google Scholar
[24] Marsh S P 1980 LASL Shock Hugoniot Data (Berkeley: University of California Press)
[25] Liu H, Tse J S, Nellis W J 2015 Sci. Rep. 5 12823
Google Scholar
[26] Matsunaga K, Tanaka T, Yamamoto T, Lkuhara Y 2003 Phys. Rev. B 68 085110
Google Scholar
[27] Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. : Condens. Matter 14 2717
Google Scholar
[28] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133
Google Scholar
[29] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[30] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[31] Fischer T H, Almlof J 1992 J. Phys. Chem. 96 9768
Google Scholar
[32] 贾婉丽, 周淼, 王馨梅, 纪卫莉 2018 67 107102
Google Scholar
Jia W L, Zhou M, Wang X M, Ji W L 2018 Acta Phys. Sin. 67 107102
Google Scholar
[33] Brown G F, Wu J Q 2009 Laser Photon. Rev. 3 394
Google Scholar
[34] Ching W Y, Xu Y N 1994 J. Am. Ceram. Soc. 77 404
Google Scholar
[35] Wu J, Walukiewicz W, Shan W, Yu K M, Ager Ⅲ J W, Li S X, Haller E E, Lu H, Schaff W J 2003 J. Appl. Phys. 94 4457
Google Scholar
[36] French R H 1990 J. Am. Ceram. Soc. 73 477
Google Scholar
[37] Holm B, Ahuja R, Yourdshahyan Y, Johansson B, Lundqvist B I 1999 Phys. Rev. B 59 12777
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7341
- PDF Downloads: 66
- Cited By: 0
