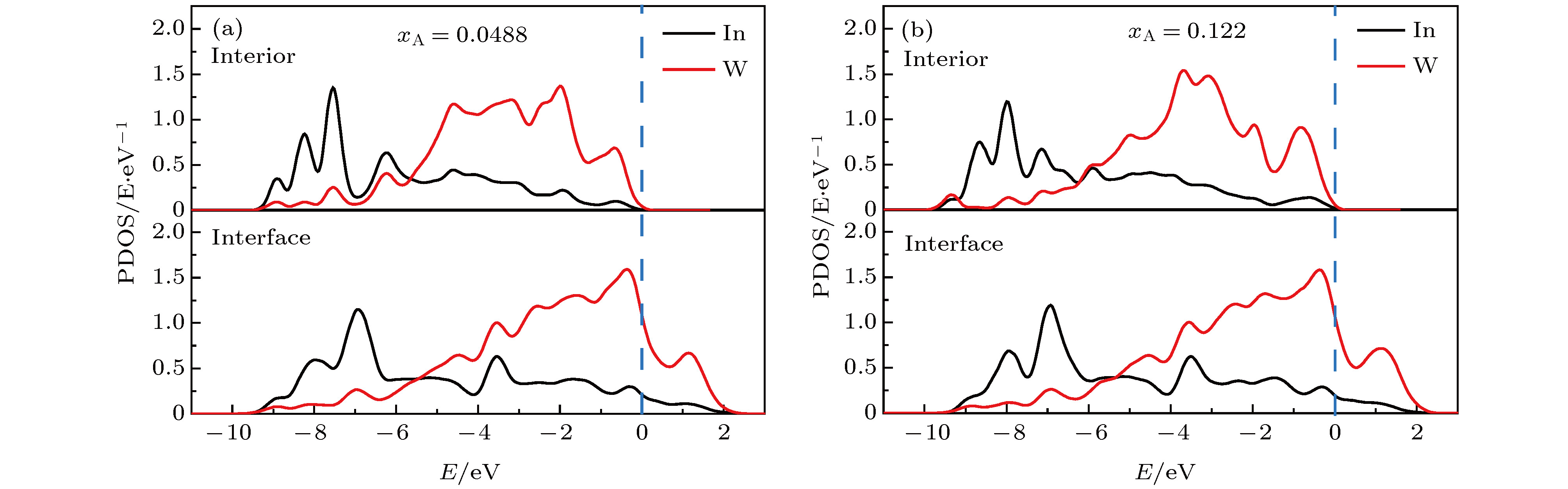
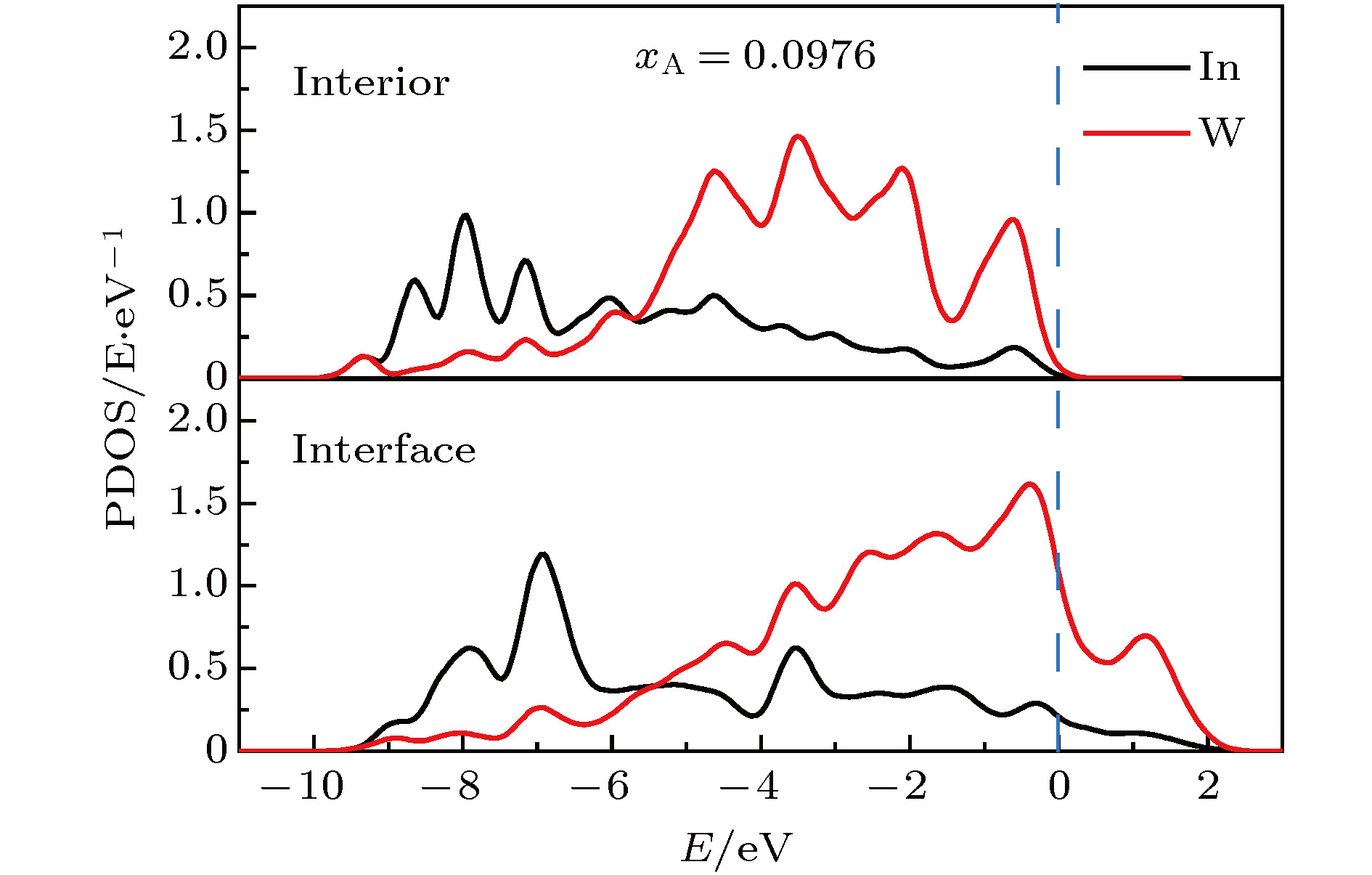
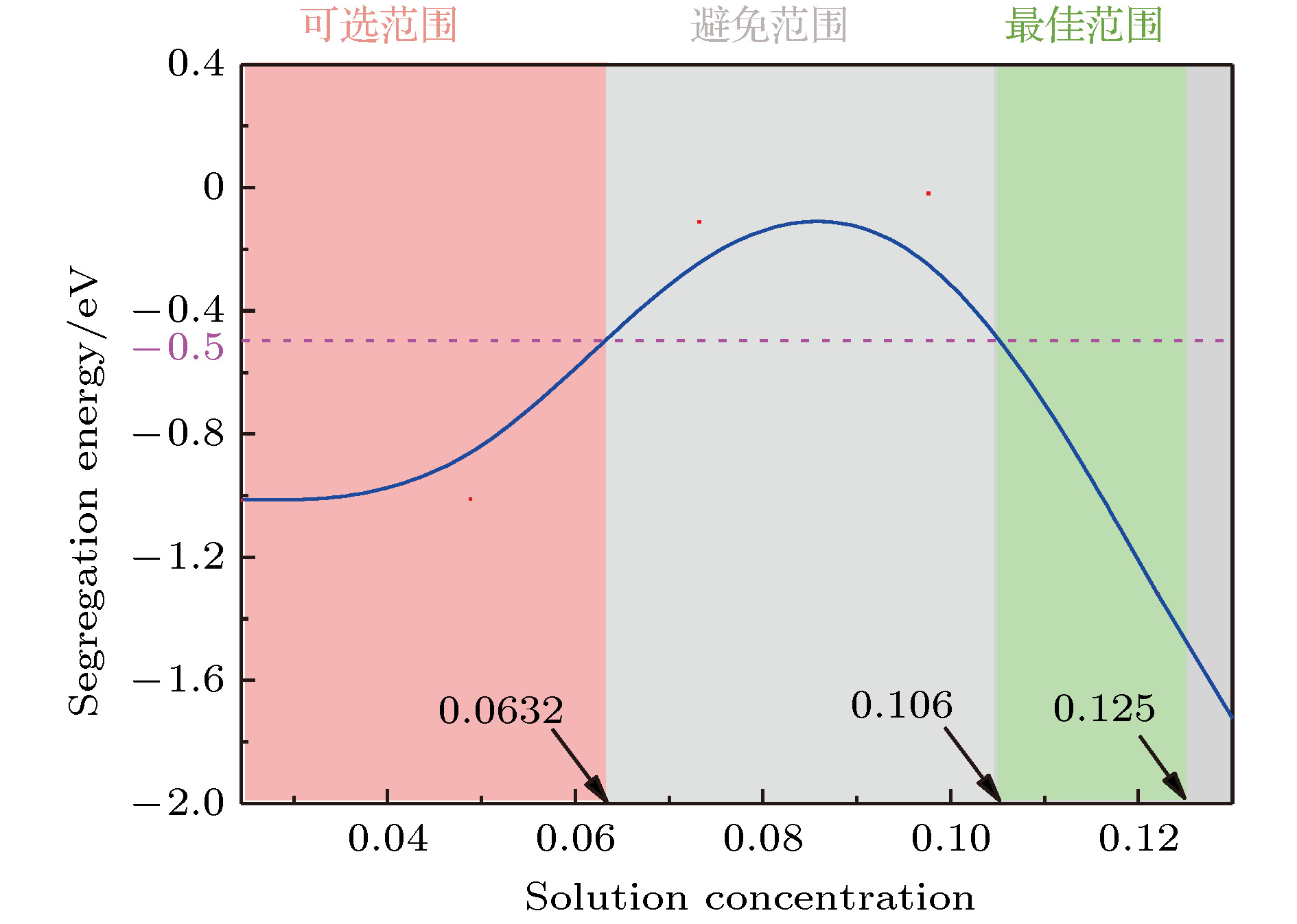
-
基于第一性原理构建了钨基合金体系的溶质偏聚模型, 以W-In体系为例研究了不同浓度下溶质的晶界偏聚行为和成键特征, 从电子结构层面揭示了W-In体系的键合作用, 预测了W-In体系界面稳定性随溶质浓度的变化规律. 结合键布居、电荷密度、差分电荷密度和态密度等电子结构分析, 发现了W-In体系中溶质原子在偏聚过程中的键性转变特征, 阐明了W-In键由晶粒内部的离子键过渡为晶界区域强共价键的微观机理. 模型计算首次得到了W-In体系中溶质本征偏聚能随In浓度的非单调变化规律, 结合键合作用和能量分析揭示了溶质浓度对本征偏聚能的影响机制. 计算预测了W-In体系达到高热稳定性所需的最佳溶质浓度范围和应避开的溶质浓度范围. 本研究为具有高温稳定性的钨基合金材料的设计与制备提供了理论基础和定量化指导.In a tungsten-based alloy system, the appropriate solute elements are selected to produce strong segregation effect to reduce the interfacial formation energy, which can effectively improve the mechanical property and thermal stability of the system. Based on the first principles calculation, the solute segregation model of tungsten-based alloys is constructed. The W-In alloy is taken for example to study the grain boundary segregation behavior and bonding characteristics of solute at different concentrations. The bonding of the W-In system is revealed from the electronic structure, and the variation of the interface stability of the W-In system with the solute concentration is predicted. Based on the electronic structure analysis of bond population, differential charge density and density of states, the bond transition characteristics of solute atoms in the W-In system in the segregation process are found, and the microscopic mechanism of the W-In bond transitioning from the ionic bond inside the grain to the strong covalent bond in the grain boundary region is elucidated: the difference between the grain boundary and the intragranular structure leads to a decrease in the valence state of the W atom in the grain boundary and the oxidizability is weakened, eventually leading to the W-In bond transition. The non-monotonic variation of the intrinsic segregation energy of the solute with the concentration of In in the W-In system is obtained. The mechanism of the influence of solute concentration on the intrinsic segregation energy is revealed by analyzing the bond interaction and energy: the solute concentration remarkably affects the bond strength before and after the W-In bond segregation, resulting in a significant decrease in the segregation ability when the solute concentration is close to 0.0976, and finally the variation of the segregation energy with solute concentration is obtained. Based on the analysis of the phase mechanical stability and the solute segregation in the grain boundary, without considering the vacancy concentration, the optimal solute concentration range and the range that needs to be circumvented in the W-In alloy system with high thermal stability are predicted by the calculations of the model, which are 0.106−0.125 and 0.0632−0.106, respectively. This study provides theoretical basis and quantitative guidance for designing and preparing the tungsten-based alloy materials with high thermal stability.
[1] Zhou X Q, Li S K, Liu J X, Wang Y C, Wang X 2010 Mater. Sci. Eng. A 527 4881
Google Scholar
[2] Scapin M 2015 Int. J. Refract. Met. Hard Mater. 50 258
Google Scholar
[3] Nguyen Manh D, Muzyk M, Kurzydlowski K J, Baluc N L, Rieth M, Dudarev S L 2011 Key Eng. Mater. 465 15
Google Scholar
[4] Tschopp M A, Murdoch H A, Kecskes L J, Darling K A 2014 JOM 66 1000
[5] Posthill J B, Hogwood M C, Edmonds D V 1986 Powder Metall. 29 45
[6] Gul H, Uysal M, Çetinkaya T, Guler M O, Alp A, Akbulut H 2014 Int. J. Hydrogen Energ. 39 21414
Google Scholar
[7] Millett P C, Selvam R P, Saxena A 2007 Acta Mater. 55 2329
Google Scholar
[8] Hirouchi T, Takaki T, Tomita Y 2010 Int. J. Mech. Sci. 52 309
Google Scholar
[9] Song X, Zhang J, Li L, Yang K, Liu G 2006 Acta Mater. 54 5541
Google Scholar
[10] Liu F, Kirchheim R 2004 Scr. Mater. 51 521
Google Scholar
[11] Liu F, Kirchheim R 2004 J. Cryst. Growth 264 385
Google Scholar
[12] Liu F, Yang G, Kirchheim R 2004 J. Cryst. Growth 264 392
Google Scholar
[13] Liu F, Kirchheim R 2004 Thin Solid Films 466 108
Google Scholar
[14] Darling K A, Vanleeuwen B K, Koch C C, Scattergood R O 2010 Mater. Sci. Eng. A 527 3572
Google Scholar
[15] Chookajorn T, Murdoch H A, Schuh C A 2012 Science 337 951
Google Scholar
[16] Kawazoe Y 2001 Mater. Design 22 61
Google Scholar
[17] Bond A D, Solanko K A, Jacco V D S, Neumann M A 2011 CrystEngComm 13 1768
Google Scholar
[18] Braithwaite J S, Rez P 2005 Acta Mater. 53 2715
Google Scholar
[19] Yamaguchi M, Kaburaki H, Shiga M 2004 J. Phys.:Condens. Matter 16 3933
Google Scholar
[20] Reza M, Laws K J, Nikki S, Michael F 2018 Acta Mater. 158 257
Google Scholar
[21] Wu X, You Y W, Kong X S, Chen J L, Luo G N, Lu G H, Liu C S, Wang Z 2016 Acta Mater. 120 315
Google Scholar
[22] 孟凡顺, 李久会, 赵星 2014 23 237102
Google Scholar
Meng F, Li J H, Zhao X 2014 Acta Phys. Sin. 23 237102
Google Scholar
[23] Tang F, Liu X, Wang H, Hou C, Lu H, Nie Z, Song X 2019 Nanoscale 11 1813
Google Scholar
[24] Scheiber D, Pippan R, Puschnig P, Ruban A, Romaner L 2016 Int. J. Refract. Met. Hard Mater. 60 75
Google Scholar
[25] Segall M D, Lindan P J D, Probert M J 2002 J. Phys.:Condens. Matter 14 2717
Google Scholar
[26] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[27] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[28] Ceperley D M, Alder B J 1980 Phys. Rev. Lett. 45 566
Google Scholar
[29] Pfrommer B G, Cote M, Louie S G, Cohen M L 1997 J. Comput. Phys. 131 233
Google Scholar
[30] Scheiber D, Razumovskiy V I, Puschnig P, Pippan R, Romaner L 2015 Acta Mater. 88 180
Google Scholar
[31] Zdanuk E J, Krock R H 1969 US Patent 3 423 203
[32] Chelikowsky J R, Cohen M L 1976 Phys. Rev. B 14 556
Google Scholar
[33] Trelewicz J R, Schuh C A 2009 Phys. Rev. B 79 094112
Google Scholar
[34] Asta M, Wolverton C, Ozoliņš V 2004 Phys. Rev. B 69 144109
Google Scholar
-
图 1
$ {\varSigma 3} $ {111}$\left\langle {\; 1\; \bar1 \; 0\; } \right\rangle $ 晶界模型和溶质偏聚位点示意图Fig. 1. Diagram of
$ {\varSigma 3} $ {111}$\left\langle {\; 1\; \bar1 \; 0\; } \right\rangle $ grain boundary model and solute segregation sites.
图 2 不同溶质浓度下晶内和晶界区域的W—In键Mulliken布居分析 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
Fig. 2. Mulliken population analysis of W—In bond at grain interior and grain boundary at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122.
图 3 不同溶质浓度下W-In界面特性的电荷密度和差分电荷密度 (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
Fig. 3. Charge density and charge density difference of W-In interface characteristics at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.0732; (c) xA = 0.122
图 4 不同溶质浓度晶内和晶界区域W和In原子的PDOS (a) xA = 0.0488; (b) xA = 0.122
Fig. 4. PDOS of W and In atoms at grain interior and grain boundary at different solute concentrations: (a) xA = 0.0488; (b) xA = 0.122
图 5 不同位点下偏聚能随溶质浓度的变化关系
Fig. 5. Segregation energy as a function of solute concentration corresponding to different sites.
图 6 溶质浓度为0.0976时溶质偏聚前后体系晶内和晶界区域W和In原子PDOS
Fig. 6. PDOS of W and In atoms at grain interior and grain boundary before and after segregation at solute concentration of 0.0976.
图 7 W-In体系溶质浓度选取范围示意图
Fig. 7. Diagram of solute concentration selection range in W-In system.
表 1 不同溶质浓度下的W-In体系弹性常数计算结果
Table 1. Calculation results of elastic constants of W-In system at different solute concentrations. GPa
溶质浓度 C11 C12 C44 C11 – C12 C11 + 2C12 0 501.5 203.4 127.2 298.1 908.3 0.0625 488.0 201.7 140.0 246.3 2128.5 0.125 364.5 222.3 143.9 220.6 809.1 0.25 208.0 245.9 138.6 –37.9 699.8 
下载: 导出CSV
-
[1] Zhou X Q, Li S K, Liu J X, Wang Y C, Wang X 2010 Mater. Sci. Eng. A 527 4881
Google Scholar
[2] Scapin M 2015 Int. J. Refract. Met. Hard Mater. 50 258
Google Scholar
[3] Nguyen Manh D, Muzyk M, Kurzydlowski K J, Baluc N L, Rieth M, Dudarev S L 2011 Key Eng. Mater. 465 15
Google Scholar
[4] Tschopp M A, Murdoch H A, Kecskes L J, Darling K A 2014 JOM 66 1000
[5] Posthill J B, Hogwood M C, Edmonds D V 1986 Powder Metall. 29 45
[6] Gul H, Uysal M, Çetinkaya T, Guler M O, Alp A, Akbulut H 2014 Int. J. Hydrogen Energ. 39 21414
Google Scholar
[7] Millett P C, Selvam R P, Saxena A 2007 Acta Mater. 55 2329
Google Scholar
[8] Hirouchi T, Takaki T, Tomita Y 2010 Int. J. Mech. Sci. 52 309
Google Scholar
[9] Song X, Zhang J, Li L, Yang K, Liu G 2006 Acta Mater. 54 5541
Google Scholar
[10] Liu F, Kirchheim R 2004 Scr. Mater. 51 521
Google Scholar
[11] Liu F, Kirchheim R 2004 J. Cryst. Growth 264 385
Google Scholar
[12] Liu F, Yang G, Kirchheim R 2004 J. Cryst. Growth 264 392
Google Scholar
[13] Liu F, Kirchheim R 2004 Thin Solid Films 466 108
Google Scholar
[14] Darling K A, Vanleeuwen B K, Koch C C, Scattergood R O 2010 Mater. Sci. Eng. A 527 3572
Google Scholar
[15] Chookajorn T, Murdoch H A, Schuh C A 2012 Science 337 951
Google Scholar
[16] Kawazoe Y 2001 Mater. Design 22 61
Google Scholar
[17] Bond A D, Solanko K A, Jacco V D S, Neumann M A 2011 CrystEngComm 13 1768
Google Scholar
[18] Braithwaite J S, Rez P 2005 Acta Mater. 53 2715
Google Scholar
[19] Yamaguchi M, Kaburaki H, Shiga M 2004 J. Phys.:Condens. Matter 16 3933
Google Scholar
[20] Reza M, Laws K J, Nikki S, Michael F 2018 Acta Mater. 158 257
Google Scholar
[21] Wu X, You Y W, Kong X S, Chen J L, Luo G N, Lu G H, Liu C S, Wang Z 2016 Acta Mater. 120 315
Google Scholar
[22] 孟凡顺, 李久会, 赵星 2014 23 237102
Google Scholar
Meng F, Li J H, Zhao X 2014 Acta Phys. Sin. 23 237102
Google Scholar
[23] Tang F, Liu X, Wang H, Hou C, Lu H, Nie Z, Song X 2019 Nanoscale 11 1813
Google Scholar
[24] Scheiber D, Pippan R, Puschnig P, Ruban A, Romaner L 2016 Int. J. Refract. Met. Hard Mater. 60 75
Google Scholar
[25] Segall M D, Lindan P J D, Probert M J 2002 J. Phys.:Condens. Matter 14 2717
Google Scholar
[26] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[27] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[28] Ceperley D M, Alder B J 1980 Phys. Rev. Lett. 45 566
Google Scholar
[29] Pfrommer B G, Cote M, Louie S G, Cohen M L 1997 J. Comput. Phys. 131 233
Google Scholar
[30] Scheiber D, Razumovskiy V I, Puschnig P, Pippan R, Romaner L 2015 Acta Mater. 88 180
Google Scholar
[31] Zdanuk E J, Krock R H 1969 US Patent 3 423 203
[32] Chelikowsky J R, Cohen M L 1976 Phys. Rev. B 14 556
Google Scholar
[33] Trelewicz J R, Schuh C A 2009 Phys. Rev. B 79 094112
Google Scholar
[34] Asta M, Wolverton C, Ozoliņš V 2004 Phys. Rev. B 69 144109
Google Scholar
下载:
计量
- 文章访问数: 10917
- PDF下载量: 122
- 被引次数: 0
