-
Antiferromagnets (AFM) are promising for future spintronic applications due to their advantageous properties. Antiferromagnets produce no stray fields and are insensitive to external magnetic field perturbations. Furthermore, antiferromagnets show intrinsic high terahertz (THz) frequency dynamics. The THz pulses are a direct and general probe of ultrafast spin dynamics in insulating antiferromagnets. In this review article, we discuss the excitation and control of the antiferromagnetic spin resonances in rare-earth orthoferrites (RFeO3, R indicates Y and rare-earth element) with the THz electromagnetic pulsetime-domain spectroscopy. We believe that this approach is general and can be applied to a broad range of materials with different AFM spin alignments, giving a novel non-contact approach to probing AFM order with ps temporal resolution. We summarize different quasi-ferromagnetic modes (qFM) and quasi-antiferromagnetic modes (qAFM), as well as the spin reorientation transition temperatures of RFeO3. Coherent control of spin waves at THz frequency promises fruitful applications in ultrafast magnetization control and has received increasing attention. It is demonstrated that not only the delay time between the excitation and control THz pulses arriving DyFeO3, but also the intrinsic dielectric anisotropy of YFeO3 in the THz range allow the coherent control of both the amplitude and the phase of the excited spin waves. Moreover, we outline the current observation of Dicke cooperativity in magnetic interaction of ErxY1－xFeO3, which presents a route to understanding, controlling, and predicting novel phases of condensed matter by using the concepts and tools available in quantum optics. Finally, magnon-polaritonsare demonstrated to play a key role in preparing the THz waves through TmFeO3.
[1] Jungwirth T, Marti X, Wadley P, Wunderlich J 2016 Nat. Nanotechnol. 11 231
Google Scholar
[2] Baltz V, Manchon A, Tsoi M, Moriyama T, Ono T, Tserkovnyak Y 2018 Rev. Mod. Phys. 90 015005
Google Scholar
[3] Kimel A V, Kirilyuk A, Tsvetkov A, Pisarev R V, Rasing T 2004 Nature 429 850
Google Scholar
[4] de Jong J A, Razdolski I, Kalashnikova A M, Pisarev R V, Balbashov A M, Kirilyuk A, Kimel A V 2012 Phys. Rev. Lett. 108 157601
Google Scholar
[5] Kirilyuk A, Kimel A V, Rasing T 2010 Rev. Mod. Phys. 82 2731
Google Scholar
[6] Satoh T, Cho S J, Iida R, Shimura T, Kuroda K, Ueda H, Ueda Y, Ivanov B A, Nori F, Fiebig M 2010 Phys. Rev. Lett. 105 077402
Google Scholar
[7] Milano J, Steren L B, Grimsditch M 2004 Phys. Rev. Lett. 93 077601
Google Scholar
[8] Nishitani J, Nagashima T, Hangyo M 2012 Phys. Rev. B 85 174439
Google Scholar
[9] Mikhaylovskiy R V, Hendry E, Secchi A, Mentink J H, Eckstein M, Wu A, Pisarev R V, Kruglyak V V, Katsnelson M I, Rasing T, Kimel A V 2015 Nat. Commun. 6 8190
Google Scholar
[10] Jin Z, Tkach A, Casper F, Spetter V, Grimm H, Thomas A, Kampfrath T, Bonn M, Kläui M, Turchinovich D 2015 Nat. Phys. 11 761
Google Scholar
[11] Kampfrath T, Tanaka K, Nelson K A 2013 Nat. Photon. 7 680
Google Scholar
[12] Kampfrath T, Sell A, Klatt G, Pashkin A, Mährlein S, Dekorsy T, Wolf M, Fiebig M, Leitenstorfer A, Huber R 2011 Nat. Photon. 5 31
Google Scholar
[13] Yamaguchi K, Nakajima M, Suemoto T 2010 Phys. Rev. Lett. 105 237201
Google Scholar
[14] Yamaguchi K, Kurihara T, Minami Y, Nakajima M, Suemoto T 2013 Phys. Rev. Lett. 110 137204
Google Scholar
[15] Kimel A V, Kirilyuk A, Usachev P A, Pisarev R V, Balbashov A M, Rasing T 2005 Nature 435 655
Google Scholar
[16] Jiang J, Jin Z, Song G, Lin X, Ma G, Cao S 2013 Appl. Phys. Lett. 103 062403
Google Scholar
[17] Jin Z, Mics Z, Ma G, Cheng Z, Bonn M, Turchinovich D 2013 Phys. Rev. B 87 094422
Google Scholar
[18] Nova T F, Cartella A, Cantaluppi A, Först M, Bossini D, Mikhaylovskiy R V, Kimel A V, Merlin R, Cavalleri A 2017 Nat. Phys. 13 132
Google Scholar
[19] Baierl S, Hohenleutner M, Kampfrath T, Zvezdin A K, Kimel A V, Huber R, Mikhaylovskiy R V 2016 Nat. Photon. 10 715
Google Scholar
[20] Mikhaylovskiy R V, Huisman T J, Pisarev R V, Rasing T, Kimel A V 2017 Phys. Rev. Lett. 118 017205
Google Scholar
[21] Kurihara T, Watanabe H, Nakajima M, Karube S, Oto K, Otani Y, Suemoto T 2018 Phys. Rev. Lett. 120 107202
Google Scholar
[22] Li X, Bamba M, Yuan N, Zhang Q, Zhao Y, Xiang M, Xu K, Jin Z, Ren W, Ma G, Cao S, Turchinovich D, Kono J 2018 Science 361 794
Google Scholar
[23] Wang Z Q, Lan Y S, Zeng Z Y, Chen X R, Chen Q F 2019 Solid State Commun. 288 10
Google Scholar
[24] Mukhin A A, Biberacher M, Pimenov A, Loidl A 2004 J. Magn. Reson. 170 8
Google Scholar
[25] Sihvola A 2007 Metamaterials 1 2
Google Scholar
[26] Gollub J N, Chin J Y, Cui T J, Smith D R 2009 Opt. Express 17 2122
Google Scholar
[27] Iida R, Satoh T, Shimura T, Kuroda K, Ivanov B, Tokunaga Y, Tokura Y 2011 Phys. Rev. B 84 064402
Google Scholar
[28] Song G, Jin Z, Lin X, Jiang J, Wang X, Wu H, Ma G, Cao S 2014 J. Appl. Phys. 115 163108
Google Scholar
[29] Zhou R, Jin Z, Li G, Ma G, Cheng Z, Wang X 2012 Appl. Phys. Lett. 100 061102
Google Scholar
[30] Song G, Jiang J, Wang X, Jin Z, Lin X, Ma G, Cao S 2013 J. Appl. Phys. 114 243104
Google Scholar
[31] Fu X, Xi X, Bi K, Zhou J 2013 Appl. Phys. Lett. 103 211108
Google Scholar
[32] Kozlov G V, Lebedev S P, Mukhin A A, Prokhorov A S, Fedorov I V, Balbashov A M, Parsegov I Y 1993 IEEE Trans. Magn. 29 3443
Google Scholar
[33] Zeng X, Fu X, Wang D, Xi X, Zhou J, Li B 2015 Opt. Express 23 31956
Google Scholar
[34] Fu X, Zeng X, Wang D, Zhang H C, Han J, Cui T J 2015 Sci. Rep. 5 14777
Google Scholar
[35] Liu X, Jin Z, Zhang S, Zhang K, Zhao W, Xu K, Lin X, Cheng Z, Cao S, Ma G 2017 J. Phys. D: Appl. Phys. 51 024001
[36] Liu X, Xie T, Guo J, Yang S, Song Y, Lin X, Cao S, Cheng Z, Jin Z, Wu A, Ma G, Yao J 2018 Appl. Phys. Lett. 113 022401
Google Scholar
[37] Dan'shin N K, Kramarchuk G G, Sdvizhkov M A 1986 JETP Lett. 44 85
[38] Nikolov O, Hall I, Barilo S N, Guretskii S A 1994 J. Phys. Condens. Matter 6 3793
[39] Zhang K, Xu K, Liu X, Zhang Z, Jin Z, Lin X, Li B, Cao S, Ma G 2016 Sci. Rep. 6 23648
Google Scholar
[40] White R 1969 J. Appl. Phys. 40 1061
[41] Fu X, Liu X, Zhou J 2014 Mater. Lett. 132 190
Google Scholar
[42] Lin X, Jiang J, Jin Z, Wang D, Tian Z, Han J, Cheng Z, Ma G 2015 Appl. Phys. Lett. 106 092403
Google Scholar
[43] Jiang J, Song G, Wang D, Jin Z, Tian Z, Lin X, Han J, Ma G, Cao S, Cheng Z 2016 J. Phys. Condens. Matter 28 116002
Google Scholar
[44] Todorov Y, Andrews A M, Colombelli R, Liberato S D, Ciuti C, Klang P, Strasser G, Sirtori C 2010 Phys. Rev. Lett. 105 196402
Google Scholar
[45] Forn-Díaz P, Lamata L, Rico E, Kono J, Solano E 2019 Rev. Mod. Phys. 91 025005
[46] Herrmann G F 1963 J. Phys. Chem. Solids 24 597
Google Scholar
[47] Grishunin K, Huisman T, Li G, Mishina E, Rasing T, Kimel A V, Zhang K, Jin Z, Cao S, Ren W, Ma G, Mikhaylovskiy R V 2018 ACS Photon. 5 1375
Google Scholar
-
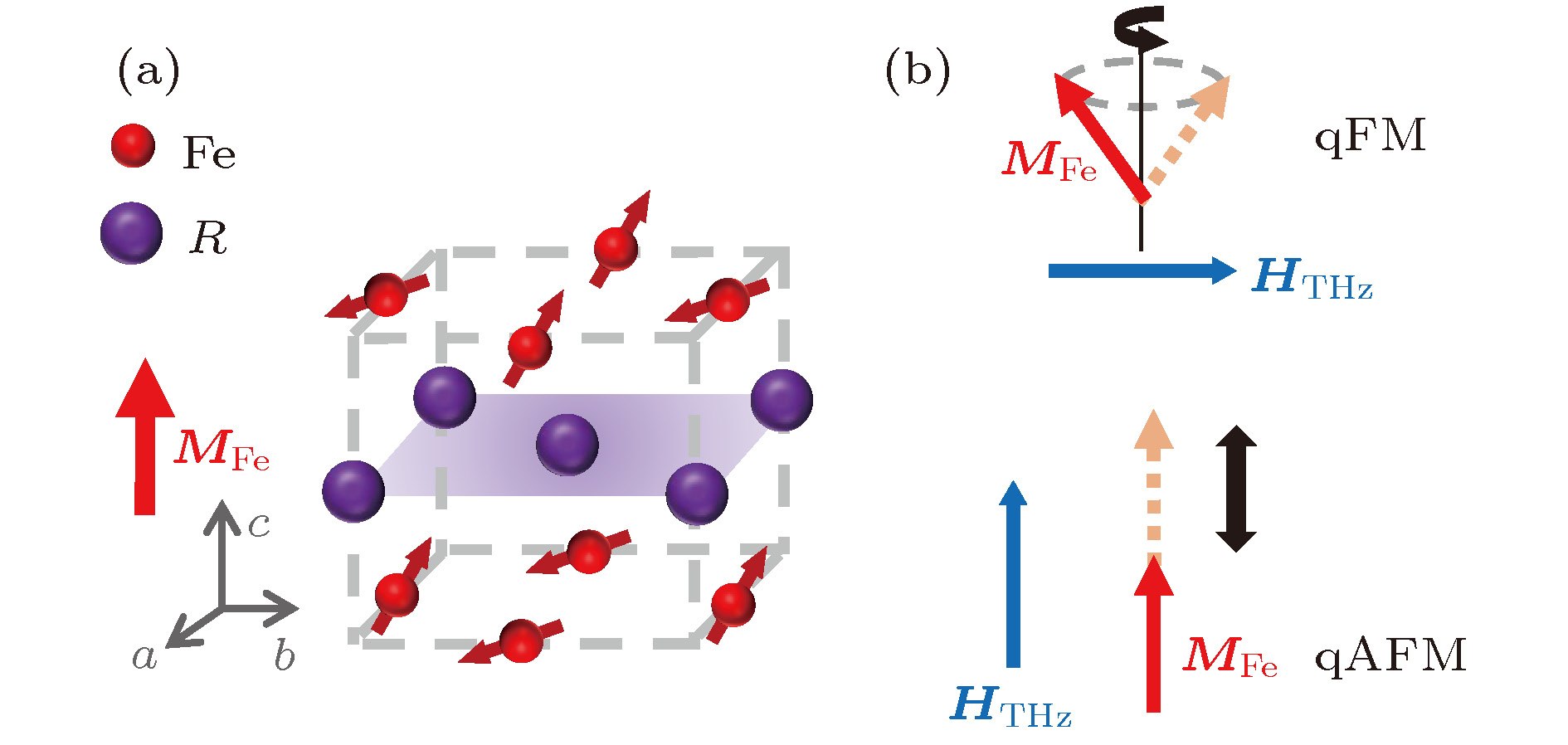
图 1 (a) RFeO3反铁磁晶体晶体结构与自旋结构, 邻近的
${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ 离子沿着a轴反平行有序排列; (b) THz激发的准铁磁模式(qFM)和准反铁磁(qAFM)模式Figure 1. (a) Lattice and spin structure of RFeO3, adjacent
${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ ions are antiparallel and ordered along the a axis; (b) THz excitation of qFM mode and qAFM mode.
图 2 (a), (b)分别为激发qFM模式(红色)与qAFM模式(蓝色)时的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅里叶变换光谱
Figure 2. (a), (b) THz time-domain transmission spectrum of qFM mode (red curve) and qAFM mode (blue curve), the insets are enlarged versions of the oscillating sections; (c), (d) Fourier transform spectra of the oscillating parts.
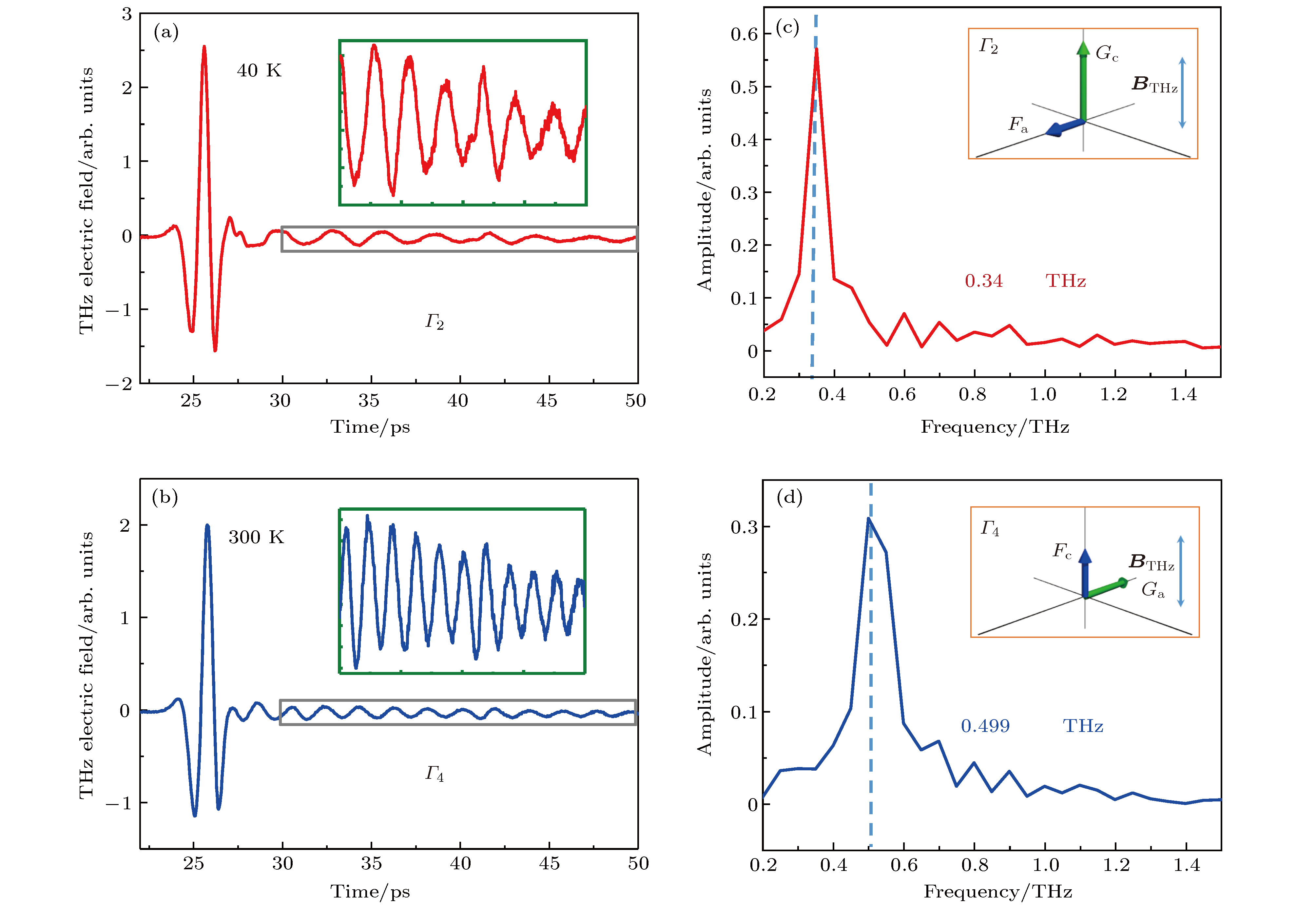
图 3 (a), (b) 40 K和300 K时
${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ 的THz时域透射谱, 插图为振荡部分的放大图; (c), (d)分别为振荡部分的傅立叶变换光谱, 插图为${\varGamma _2}$ 与${\varGamma _{\rm{4}}}$ 的示意图Figure 3. (a), (b) THz time-domain transmission spectra of
${\rm{ErFe}}{{\rm{O}}_{\rm{3}}}$ at 40 K and 300 K; (c), (d) Fourier transform spectra of the oscillating signals. Insets: schematic diagram of${\varGamma _2}$ and${\varGamma _{\rm{4}}}$ .
图 4 (a) THz脉冲激发qFM模式; (b) THz脉冲激发qAFM模式; (c) THz脉冲同时激发qFM和qAFM模式, 当Δt为qFM(qAFM)振荡周期的1.5倍时, 该自旋进动被有效地抑制; (d)图(c)中振荡部分的傅里叶变换光谱
Figure 4. (a) THz pulses excite qFM mode; (b) THz pulse excited the qAFM mode; (c) THz pulse excites both qFM mode and qAFM mode, as the interval time is 1.5 times of the qFM (qAFM) oscillation period, the spin precession is suppressed; (d) Fourier transform spectra of the oscillating parts in (c).
图 5 当
$\theta $ = 0°, 45°, 90°时, 透过样品后THz波的电场强度,$\theta $ 的定义如插图所示; (b)振荡部分的放大, 其时域区间为10−25 ps范围内的THz电场, 实线是单指数衰减拟合; (c), (d) qFM模式自旋振荡部分的傅立叶变换得到振幅和相位随方位角$\theta $ 的变化[17]Figure 5. (a) THz electric fields transmitted through the YFeO3, as
$\theta $ = 0°, 45° and 90°; (b) the oscillating parts of the (a) from 10 ps to 25 ps, the solid line is a single exponential decay fitting; (c) amplitude and (d) phase varies with the angle$\theta $ , by using the Fourier transform of the spin oscillating of qFM mode [17]. Reproduced with permission from Ref.[17]
图 6 (a) ErFeO3中的Er3+离子由于多重效应的能级分裂示意图; (b)从0 T到10 T不同磁场下的吸收系数谱, 白色虚线为Fe3+的qFM磁振模式; (c)计算得到不同磁场下晶体场的双重态
$\left| {i = 1} \right\rangle $ 和$\left| {i = 2} \right\rangle $ [22]Figure 6. (a) Energy level splitting scheme of
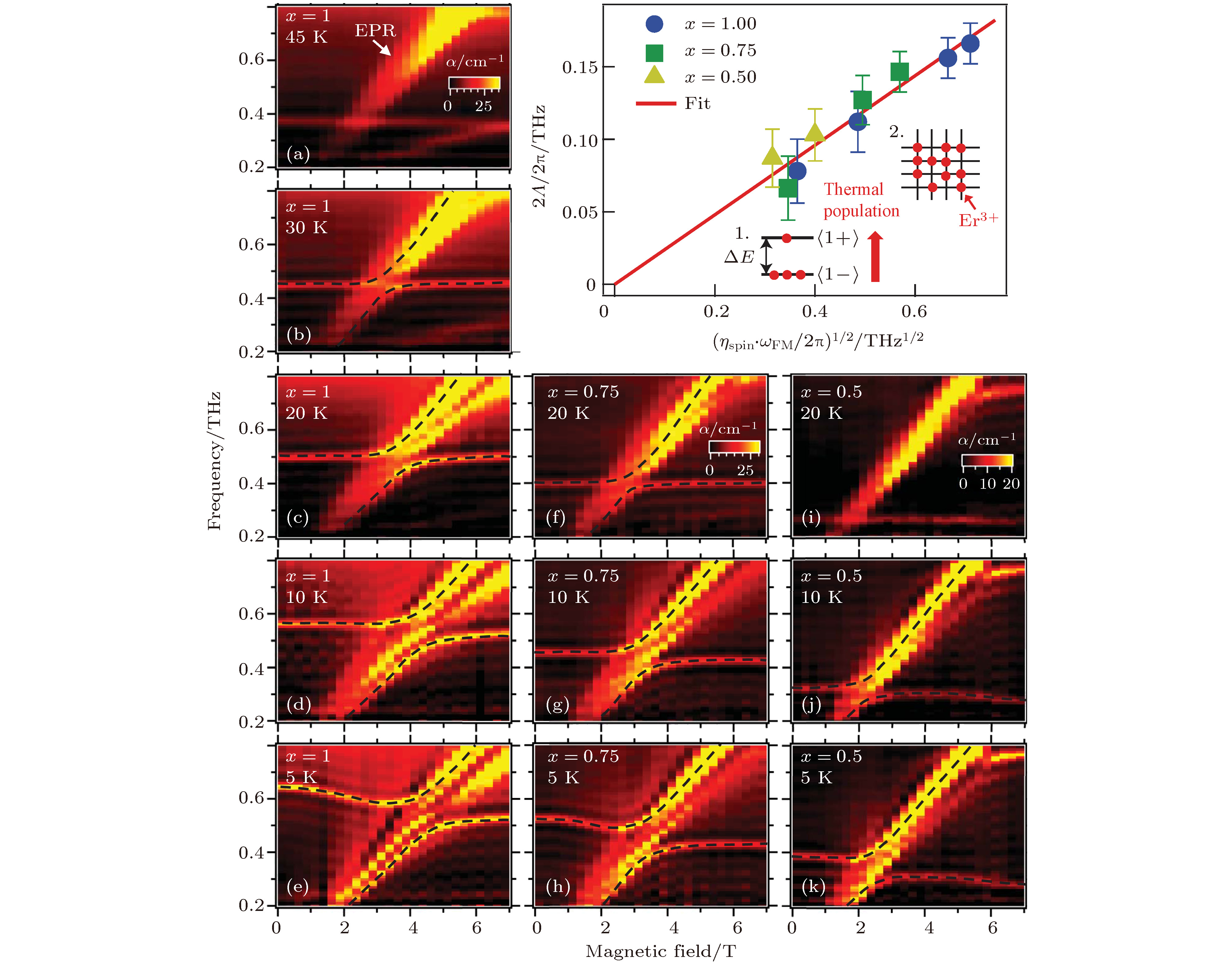
${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ ions due to multiple effects; (b) absorption coefficient spectra at various magnetic fields from 0 T to 10 T, the white dashed line is the${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ qFM magnon mode; (c) calculated energy levels for the$\left| {i = 1} \right\rangle $ and$\left| {i = {\rm{2}}} \right\rangle $ crystal-field doublets as a function of magnetic field[22].
图 7 Er3+的自旋和Fe3+的qFM真空磁子间关联耦合的实验验证 (a)−(k)不同温度和Y3+掺杂时的吸收光谱, 图中的虚线用来帮助识别杂化模式; (l)耦合系数Λ正比于
$\sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ , 图为两种机制来决定实验中的${\eta _{{\rm{spin}}}}$ [22]Figure 7. Experimental evidence for cooperative coupling between paramagnetic
${\rm{E}}{{\rm{r}}^{{\rm{3 + }}}}$ spins and${\rm{F}}{{\rm{e}}^{{\rm{3 + }}}}$ vacuum magnons: (a)−(k) Absorption spectra measured at various temperatures and${{\rm{Y}}^{{\rm{3 + }}}}$ doping levels, dashed black lines are guides to the eye for identifying the hybridized modes; (l) the coupling rate Λ is proportionality with$\sqrt {{\eta _{{\rm{spin}}}}{\omega _{{\rm{FM}}}}} $ , the inset shows two types of mechanisms that determine${\eta _{{\rm{spin}}}}$ in the measurements[22]. Reproduced with permission from Ref.[22].
图 8 (a) 透过TmFeO3晶体的THz时域波形及其(b)傅里叶变换谱; (c) TmFeO3薄片的THz产生波形及其相应的(d)傅里叶变换谱; (e)自旋共振附近的磁子-极化子色散关系[47]
Figure 8. (a) THz waveforms transmitted through the TmFeO3 sample and (b) its Fourier transforms of the time traces; (c) THz generation in a TmFeO3 slab by a laser pulse and (d) its Fourier spectra shown in (c); (e) the magnon-polariton dispersion in the vicinity of the spin resonance[47] . Reproduced with permission from Ref.[47]
表 1 RFeO3的qFM和qAFM模式的自旋共振频率
Table 1. The qFM and qAFM mode resonance frequencies of rare earth orthoferrite
RFeO3 υqFM/THz υqAFM/THz Reference YFeO3 0.299(300K) 0.527(300K) [13 29] PrFeO3 0.34(300K) 0.41(300K) [30] NdFeO3 0.28(300K) 0.485(290K) [16] GdFeO3 0.305(300K) 0.606(300K) [31] TbFeO3 0.322(300K) 0.537(300K) [32] HoFeO3 0.37(270K) 0.57(270K) [33] ErFeO3 0.377(300K) 0.673(300K) [14] TmFeO3 0.402(300K) 0.698(300K) [32] DyFeO3 0.379(300K) 0.51(300K) [32] SmFeO3 0.34(200K) 0.62(200K) [34] 
DownLoad: CSV
表 2 SmxDy1–xFeO3单晶在40K的qFM模式的自旋共振频率与Sm浓度的关系[35]
Table 2. Resonance frequencies of qFM mode for the single crystals versus Sm concentration at 40 K[34]
RFeO3 υqFM/THz DyFeO3 0.2(40K) Sm0.5Dy0.5FeO3 0.35(40K) Sm0.6Dy0.4FeO3 0.39(40K) Sm0.7Dy0.3FeO3 0.45(40K) SmFeO3 0.55(40K)
DownLoad: CSV
表 3 稀土正铁氧体的自旋重取向温区总结
Table 3. The spin reorientation temperature region of rare earth ferrite
DownLoad: CSV
表 4 SmxDy1–xFeO3的自旋重取向温度与Sm浓度的关系
Table 4. SRT temperatures for the SDFO single crystal family versus Sm concentration
RFeO3 the spin reorientation temperature region Sm0.3Dy0.7FeO3 75–105K Sm0.5Dy0.5FeO3 175–220K Sm0.6Dy0.4FeO3 235–275K
DownLoad: CSV
-
[1] Jungwirth T, Marti X, Wadley P, Wunderlich J 2016 Nat. Nanotechnol. 11 231
Google Scholar
[2] Baltz V, Manchon A, Tsoi M, Moriyama T, Ono T, Tserkovnyak Y 2018 Rev. Mod. Phys. 90 015005
Google Scholar
[3] Kimel A V, Kirilyuk A, Tsvetkov A, Pisarev R V, Rasing T 2004 Nature 429 850
Google Scholar
[4] de Jong J A, Razdolski I, Kalashnikova A M, Pisarev R V, Balbashov A M, Kirilyuk A, Kimel A V 2012 Phys. Rev. Lett. 108 157601
Google Scholar
[5] Kirilyuk A, Kimel A V, Rasing T 2010 Rev. Mod. Phys. 82 2731
Google Scholar
[6] Satoh T, Cho S J, Iida R, Shimura T, Kuroda K, Ueda H, Ueda Y, Ivanov B A, Nori F, Fiebig M 2010 Phys. Rev. Lett. 105 077402
Google Scholar
[7] Milano J, Steren L B, Grimsditch M 2004 Phys. Rev. Lett. 93 077601
Google Scholar
[8] Nishitani J, Nagashima T, Hangyo M 2012 Phys. Rev. B 85 174439
Google Scholar
[9] Mikhaylovskiy R V, Hendry E, Secchi A, Mentink J H, Eckstein M, Wu A, Pisarev R V, Kruglyak V V, Katsnelson M I, Rasing T, Kimel A V 2015 Nat. Commun. 6 8190
Google Scholar
[10] Jin Z, Tkach A, Casper F, Spetter V, Grimm H, Thomas A, Kampfrath T, Bonn M, Kläui M, Turchinovich D 2015 Nat. Phys. 11 761
Google Scholar
[11] Kampfrath T, Tanaka K, Nelson K A 2013 Nat. Photon. 7 680
Google Scholar
[12] Kampfrath T, Sell A, Klatt G, Pashkin A, Mährlein S, Dekorsy T, Wolf M, Fiebig M, Leitenstorfer A, Huber R 2011 Nat. Photon. 5 31
Google Scholar
[13] Yamaguchi K, Nakajima M, Suemoto T 2010 Phys. Rev. Lett. 105 237201
Google Scholar
[14] Yamaguchi K, Kurihara T, Minami Y, Nakajima M, Suemoto T 2013 Phys. Rev. Lett. 110 137204
Google Scholar
[15] Kimel A V, Kirilyuk A, Usachev P A, Pisarev R V, Balbashov A M, Rasing T 2005 Nature 435 655
Google Scholar
[16] Jiang J, Jin Z, Song G, Lin X, Ma G, Cao S 2013 Appl. Phys. Lett. 103 062403
Google Scholar
[17] Jin Z, Mics Z, Ma G, Cheng Z, Bonn M, Turchinovich D 2013 Phys. Rev. B 87 094422
Google Scholar
[18] Nova T F, Cartella A, Cantaluppi A, Först M, Bossini D, Mikhaylovskiy R V, Kimel A V, Merlin R, Cavalleri A 2017 Nat. Phys. 13 132
Google Scholar
[19] Baierl S, Hohenleutner M, Kampfrath T, Zvezdin A K, Kimel A V, Huber R, Mikhaylovskiy R V 2016 Nat. Photon. 10 715
Google Scholar
[20] Mikhaylovskiy R V, Huisman T J, Pisarev R V, Rasing T, Kimel A V 2017 Phys. Rev. Lett. 118 017205
Google Scholar
[21] Kurihara T, Watanabe H, Nakajima M, Karube S, Oto K, Otani Y, Suemoto T 2018 Phys. Rev. Lett. 120 107202
Google Scholar
[22] Li X, Bamba M, Yuan N, Zhang Q, Zhao Y, Xiang M, Xu K, Jin Z, Ren W, Ma G, Cao S, Turchinovich D, Kono J 2018 Science 361 794
Google Scholar
[23] Wang Z Q, Lan Y S, Zeng Z Y, Chen X R, Chen Q F 2019 Solid State Commun. 288 10
Google Scholar
[24] Mukhin A A, Biberacher M, Pimenov A, Loidl A 2004 J. Magn. Reson. 170 8
Google Scholar
[25] Sihvola A 2007 Metamaterials 1 2
Google Scholar
[26] Gollub J N, Chin J Y, Cui T J, Smith D R 2009 Opt. Express 17 2122
Google Scholar
[27] Iida R, Satoh T, Shimura T, Kuroda K, Ivanov B, Tokunaga Y, Tokura Y 2011 Phys. Rev. B 84 064402
Google Scholar
[28] Song G, Jin Z, Lin X, Jiang J, Wang X, Wu H, Ma G, Cao S 2014 J. Appl. Phys. 115 163108
Google Scholar
[29] Zhou R, Jin Z, Li G, Ma G, Cheng Z, Wang X 2012 Appl. Phys. Lett. 100 061102
Google Scholar
[30] Song G, Jiang J, Wang X, Jin Z, Lin X, Ma G, Cao S 2013 J. Appl. Phys. 114 243104
Google Scholar
[31] Fu X, Xi X, Bi K, Zhou J 2013 Appl. Phys. Lett. 103 211108
Google Scholar
[32] Kozlov G V, Lebedev S P, Mukhin A A, Prokhorov A S, Fedorov I V, Balbashov A M, Parsegov I Y 1993 IEEE Trans. Magn. 29 3443
Google Scholar
[33] Zeng X, Fu X, Wang D, Xi X, Zhou J, Li B 2015 Opt. Express 23 31956
Google Scholar
[34] Fu X, Zeng X, Wang D, Zhang H C, Han J, Cui T J 2015 Sci. Rep. 5 14777
Google Scholar
[35] Liu X, Jin Z, Zhang S, Zhang K, Zhao W, Xu K, Lin X, Cheng Z, Cao S, Ma G 2017 J. Phys. D: Appl. Phys. 51 024001
[36] Liu X, Xie T, Guo J, Yang S, Song Y, Lin X, Cao S, Cheng Z, Jin Z, Wu A, Ma G, Yao J 2018 Appl. Phys. Lett. 113 022401
Google Scholar
[37] Dan'shin N K, Kramarchuk G G, Sdvizhkov M A 1986 JETP Lett. 44 85
[38] Nikolov O, Hall I, Barilo S N, Guretskii S A 1994 J. Phys. Condens. Matter 6 3793
[39] Zhang K, Xu K, Liu X, Zhang Z, Jin Z, Lin X, Li B, Cao S, Ma G 2016 Sci. Rep. 6 23648
Google Scholar
[40] White R 1969 J. Appl. Phys. 40 1061
[41] Fu X, Liu X, Zhou J 2014 Mater. Lett. 132 190
Google Scholar
[42] Lin X, Jiang J, Jin Z, Wang D, Tian Z, Han J, Cheng Z, Ma G 2015 Appl. Phys. Lett. 106 092403
Google Scholar
[43] Jiang J, Song G, Wang D, Jin Z, Tian Z, Lin X, Han J, Ma G, Cao S, Cheng Z 2016 J. Phys. Condens. Matter 28 116002
Google Scholar
[44] Todorov Y, Andrews A M, Colombelli R, Liberato S D, Ciuti C, Klang P, Strasser G, Sirtori C 2010 Phys. Rev. Lett. 105 196402
Google Scholar
[45] Forn-Díaz P, Lamata L, Rico E, Kono J, Solano E 2019 Rev. Mod. Phys. 91 025005
[46] Herrmann G F 1963 J. Phys. Chem. Solids 24 597
Google Scholar
[47] Grishunin K, Huisman T, Li G, Mishina E, Rasing T, Kimel A V, Zhang K, Jin Z, Cao S, Ren W, Ma G, Mikhaylovskiy R V 2018 ACS Photon. 5 1375
Google Scholar
-
[1] Chen Zhao-Liang, Lu Da-Biao, Ye Xu-Bin, Zhao Hao-Ting, Zhang Jie, Pan Zhao, Chi Zhen-Hua, Cui Tian, Shen Yao, Long You-Wen. High-pressure synthesized perovskite-type CeTaN2O and its magnetic and electrical properties. Acta Physica Sinica, 2024, 73(8): 080702. doi: 10.7498/aps.73.20240025 [2] Deng Shan-Shan, Song Ping, Liu Xiao-He, Yao Sen, Zhao Qian-Yi. Enhancement of magnetic susceptibility of Mn3Sn single crystal under GPa-level uniaxial stress. Acta Physica Sinica, 2024, 73(12): 127501. doi: 10.7498/aps.73.20240287 [3] Qing Yu-Lin, Peng Xiao-Li, Wen Lin, Hu Ai-Yuan. Ground state phase transition of spin-1/2 frustration model on stacked square lattice. Acta Physica Sinica, 2022, 71(3): 037501. doi: 10.7498/aps.71.20211584 [4] Qing Yu-Lin, Peng Xiao-Li, Hu Ai-Yuan. Phase transition of spin-1 frustrated model on square-lattice bilayer. Acta Physica Sinica, 2022, 71(4): 047501. doi: 10.7498/aps.71.20211685 [5] Yi En-Kui, Wang Bin, Shen Han, Shen Bing. Properties of axion insulator candidate layered Eu1–xCaxIn2As2. Acta Physica Sinica, 2021, 70(12): 127502. doi: 10.7498/aps.70.20210042 [6] . The ground state phase transition of the spin-1/2 frustration model on a stacked square lattice. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211584 [7] Wen Lin, Hu Ai-Yuan. Effect of biquadratic exchange and anisotropy on the critical temperature of antiferromagnet. Acta Physica Sinica, 2020, 69(10): 107501. doi: 10.7498/aps.69.20200077 [8] Ren Zhuang, Cheng Long, Sergei Guretskii, Nadzeya Liubochko, Li Jiang-Tao, Shang Jia-Min, Sergei Barilo, Wu An-Hua, Alexandra Kalashnikova, Ma Zong-Wei, Zhou Chun, Sheng Zhi-Gao. Terahertz spectroscopy study of doping and magnetic field induced effects on spin reorientation in Ho1–xYxFeO3 single crystals. Acta Physica Sinica, 2020, 69(20): 207802. doi: 10.7498/aps.69.20201518 [9] Fang Yu-Qing, Jin Zuan-Ming, Chen Hai-Yang, Ruan Shun-Yi, Li Ju-Geng, Cao Shi-Xun, Peng Yan, Ma Guo-Hong, Zhu Yi-Ming. Terahertz spectroscopic characterization of spin mode and crystal-field transition in high-throughput grown $ {\bf Sm}_{ x}{\bf Pr}_{ 1– x}{\bf FeO_3} $ crystals. Acta Physica Sinica, 2020, 69(20): 209501. doi: 10.7498/aps.69.20200732[10] Zhang Shun-Nong, Zhu Wei-Hua, Li Ju-Geng, Jin Zuan-Ming, Dai Ye, Zhang Zong-Zhi, Ma Guo-Hong, Yao Jian-Quan. Coherent terahertz radiation via ultrafast manipulation of spin currents in ferromagnetic heterostructures. Acta Physica Sinica, 2018, 67(19): 197202. doi: 10.7498/aps.67.20181178 [11] Fan Zheng-Fu, Tan Zhi-Yong, Wan Wen-Jian, Xing Xiao, Lin Xian, Jin Zuan-Ming, Cao Jun-Cheng, Ma Guo-Hong. Study on ultrafast dynamics of low-temperature grown GaAs by optical pump and terahertz probe spectroscopy. Acta Physica Sinica, 2017, 66(8): 087801. doi: 10.7498/aps.66.087801 [12] Liu Kui-Li, Zhou Si-Hua, Chen Song-Ling. Exchange bias tuning of metal ions doped in CuO nanocomposites. Acta Physica Sinica, 2015, 64(13): 137501. doi: 10.7498/aps.64.137501 [13] Guo Jing, Sun Li-Ling. Phenomena and findings in pressurized alkaline iron selenide superconductors. Acta Physica Sinica, 2015, 64(21): 217406. doi: 10.7498/aps.64.217406 [14] Hu Ni, Liu Yong, Tang Wu-Feng, Pei Ling, Fang Peng-Fei, Xiong Rui, Shi Jing. Fe/Cr doping effects on the magnetism in charge-ordered manganite La0.4Ca0.6MnO3. Acta Physica Sinica, 2014, 63(23): 237502. doi: 10.7498/aps.63.237502 [15] Wang Mei-Na, Li Ying, Wang Tian-Xing, Liu Guo-Dong. Magnetic properties of multiferroic material DyMnO3 in orthorhombic structure. Acta Physica Sinica, 2013, 62(22): 227101. doi: 10.7498/aps.62.227101 [16] Hu Ni, Liu Yong, Cheng Li, Shi Jing, Xiong Rui. Mn-site Fe/Cr doping effects in charge-ordered antiferromagnetic manganite La0.4Ca0.6MnO3. Acta Physica Sinica, 2011, 60(1): 017503. doi: 10.7498/aps.60.017503 [17] Han Jiu-Rong, Jiang Xue-Fan, Liu Xian-Feng. First-principles studies of helical-spin order in frustrated triangular antiferromagnet AgCrO2. Acta Physica Sinica, 2010, 59(9): 6487-6493. doi: 10.7498/aps.59.6487 [18] Li Hong, Wang Wei-Lu, Gong Pi-Feng. Spin current of a single quantum well. Acta Physica Sinica, 2007, 56(4): 2405-2408. doi: 10.7498/aps.56.2405 [19] Teng Jiao, Cai Jian-Wang, Xiong Xiao-Tao, Lai Wu-Yan, Zhu Feng-Wu. The establishment and thermal stability of exchange bias in NiFe/FeMn bilayers. Acta Physica Sinica, 2004, 53(1): 272-275. doi: 10.7498/aps.53.272 [20] ZHONG JIAN. SPIN WAVE SPECTRUM IN HEISENBERG ANTIFERRO-MAGNETIC SUPERLATTICES. Acta Physica Sinica, 1990, 39(3): 486-490. doi: 10.7498/aps.39.486
DownLoad:
Catalog
Metrics
- Abstract views: 10311
- PDF Downloads: 174
- Cited By: 0
