-
In this paper, we investigate the phase transition of the spin-1 frustrated model on a square-lattice bilayer by the double-time Green’s function method. The effects of the interlayer coupling parameter
$ {J_c} $ and single-ion anisotropy D on phase transformation between the Nèel state (AF1) and collinear state (AF2) are explored. Our results show that if only the parameters$ {J_c} $ and D are not equal to zero at the same time, the two states can exist and have the same critical temperature at$ {J_2} = {J_1}/2 $ , which represents the nearest neighbor exchange. Under such parameters, a first-order phase transformation between these two states below the critical point can occur. For$ {J_2} \ne {J_1}/2 $ , although both states may exist, their Neel temperatures differ from each other. If the Nèel point of the AF1 (AF2) state is larger, then at very low temperature, the AF1 (AF2) state is more stable. Thus, in an intermediate temperature, a first-order phase transition between these two states may also occur.-
Keywords:
- antiferromagnetic /
- magnetic anisotropy /
- general theory and models of magnetic ordering /
- exchange and superexchange interactions
[1] Manojlović M, Pavkov M, Škrinjar M, PantićM, Kapor D, Stojanović S 2003 Phys. Rev. B 68 014435
Google Scholar
[2] Manojlović M, Pavkov M, Škrinjar M, Pantić M, Kapor D, Stojanović S 2005 Phys. Rev. B 73 132510
[3] Rutonjski M S, Radošević S M, Škrinjar M G, Pavkov-Hrvojević M V, Kapor D V, Pantić M R 2007 Phys. Rev. B 76 172506
[4] Liu G B, Liu B G 2009 J. Phys. :Condens. Matter 21 195701
Google Scholar
[5] Holt M, Sushkov O P, Stanek D, Uhrig G S 2011 Phys. Rev. B 83 144528
Google Scholar
[6] Johnston D C, McQueeney R J, Lake B, Honecker A, Zhitomirsky M E, Nath R, Furukawa Y, Antropov V P, Yogesh Singh 2011 Phys. Rev. B 84 094445
Google Scholar
[7] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[8] Schmalfuß D, Darradi R, Richter J, Schulenburg J, Ihle D 2006 Phys. Rev. Lett. 97 157201
Google Scholar
[9] Nunes W A, J Ricardo de Sousa, J Roberto Viana, Richter J 2010 J. Phys. :Condens. Matter 22 146004
Google Scholar
[10] Nunes W A, Roberto Viana, Ricardo de Sousa J 2011 J. Stat. Mech. ???? 05016
[11] Onofre R, Hamer C J, Oitmaa J 2011 J. Phys. :Condens. Matter 23 416001
Google Scholar
[12] Zhuo F, Jie Q L 2014 Phys. Rev. B 89 054418
Google Scholar
[13] Bishop R F, Li P H Y, Götze O, Richter J 2019 Phys. Rev. B 100 024401
Google Scholar
[14] 王怀玉 2012 凝聚态物理的格林函数理论 (北京: ) 第348页
Wang H Y 2012 Green’s Function in Condensed Matter Physics (Beijing: Alpha Science International Ltd and Science Press) p348 (in Chinese)
[15] Callen H B 1963 Phys. Rev. 130 890
Google Scholar
[16] Anderson F B, Callen H B 1964 Phys. Rev. 136 A1068
Google Scholar
[17] Fröbrich P, Jensen P J, Kuntz P J 2000 Eur. Phys. J. B 13 477
[18] Fröbrich P, Jensen P J, Kuntz P J, Ecker A 2000 Eur. Phys. J. B 18 579
Google Scholar
[19] Fröbrich P, Kuntz P J 2006 Phys. Rep. 432 223
Google Scholar
[20] Wang H Y, Zhai L J, Qian M 2014 J. Magn. Magn. Matter 354 309
Google Scholar
-
图 1 奈尔态和共线态的磁构型. (a), (b)和(c), (d)分别对应层间耦合为反铁磁和铁磁相互作用. 实心和空心圆圈分别描述的是自旋取向相上和向下
Figure 1. Spin configurations of the Néel and collinear states. (a), (b) and (c), (d) correspond to the interlayer coupling as antiferromagnetic and ferromagnetic interactions, respectively. The solid and empty circles represent the up-spins and down-spins, respectively.
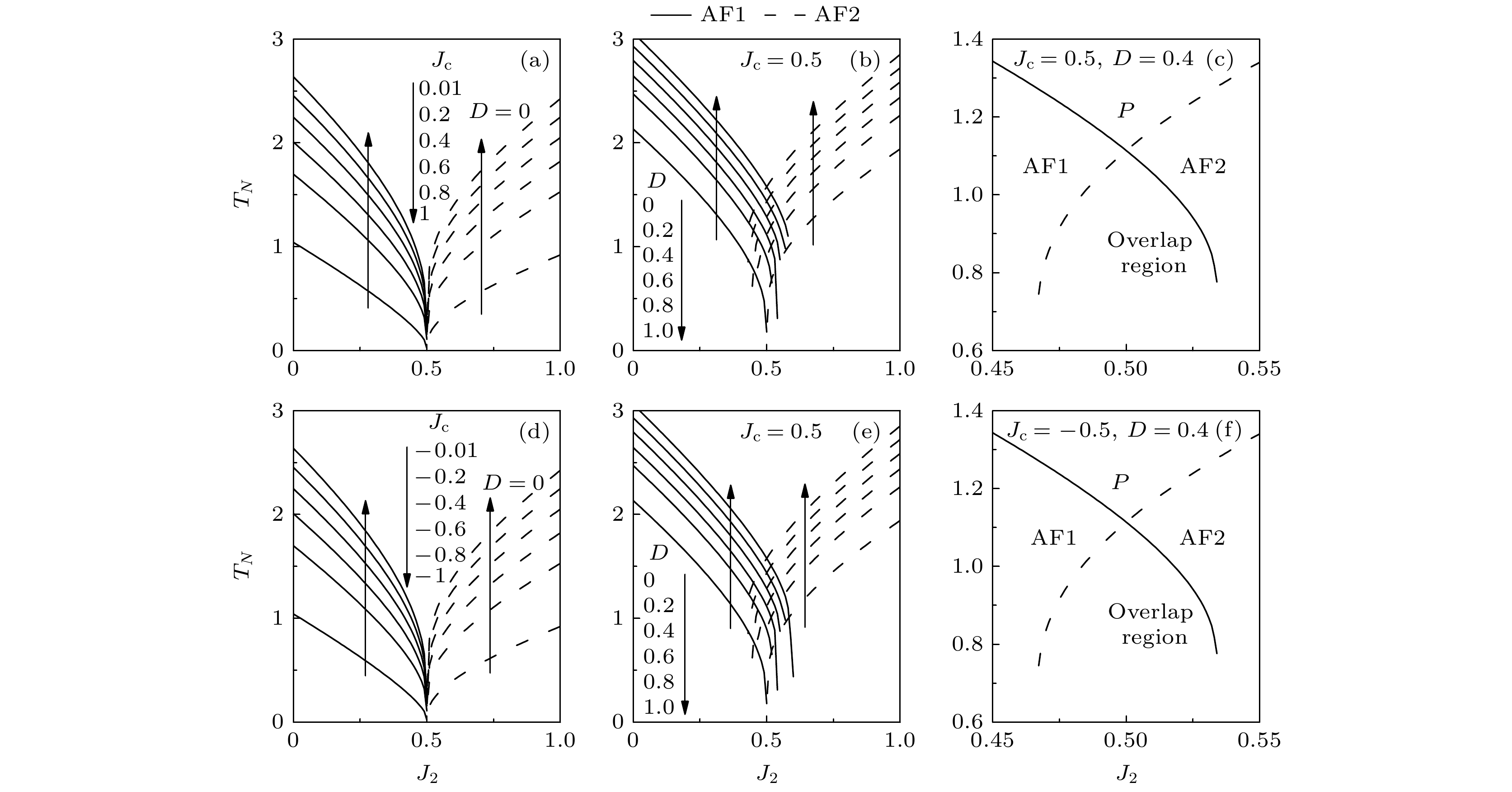
图 2 不同参数时的相变温度
$ {T_N} $ 与$ {J_2} $ 之间的变化关系 (a)$ D = 0, {J_{\text{c}}} = 0.01, 0.2, 0.4, 0.6, 0.8, 1 $ ; (b)${J_{\text{c}}} = 0.5, D = 0, 0.2, $ $ 0.4, 0.6, 0.8, 1$ ; (c)$ {J_{\text{c}}} = 0.5, D = 0.4 $ ; (d)$ D = 0, {J_{\text{c}}} = - 0.01, - 0.2, $ $ - 0.4, - 0.6, - 0.8, - 1 $ ; (e)$ {J_{\text{c}}} = - 0.5, D = 0, 0.2, 0.4, 0.6, 0.8, 1 $ ; (f)$ {J_{\text{c}}} = - 0.5, D = 0.4 $ Figure 2. Transition temperature
$ {T_N} $ as a function of$ {J_2} $ for different parameters: (a)$ D = 0, $ $ {J_{\text{c}}} = 0.01, 0.2, 0.4, 0.6, 0.8, 1 $ ; (b)${J_{\text{c}}} = $ $ 0.5, D = 0, 0.2, 0.4, 0.6, 0.8, 1$ ; (c)$ {J_{\text{c}}} = 0.5, D = 0.4 $ ; (d)$ D = 0, {J_{\text{c}}} = - 0.01, - 0.2, - 0.4, - 0.6, - 0.8, - 1 $ ; (e)${J_{\text{c}}} = - 0.5, D = 0, $ $ 0.2, 0.4, 0.6, 0.8, 1$ ; (f)$ {J_{\text{c}}} = - 0.5, D = 0.4 $ .
图 3 当
$ D = 0.01 $ 时,$ {J_{\text{c}}} \geqslant 0 $ 的自由能F与温度T之间的变化关系Figure 3. Free energy F as a function of temperature T for
$ {J_{\text{c}}} \geqslant 0 $ when$ D = 0.01 $ .
图 4 当
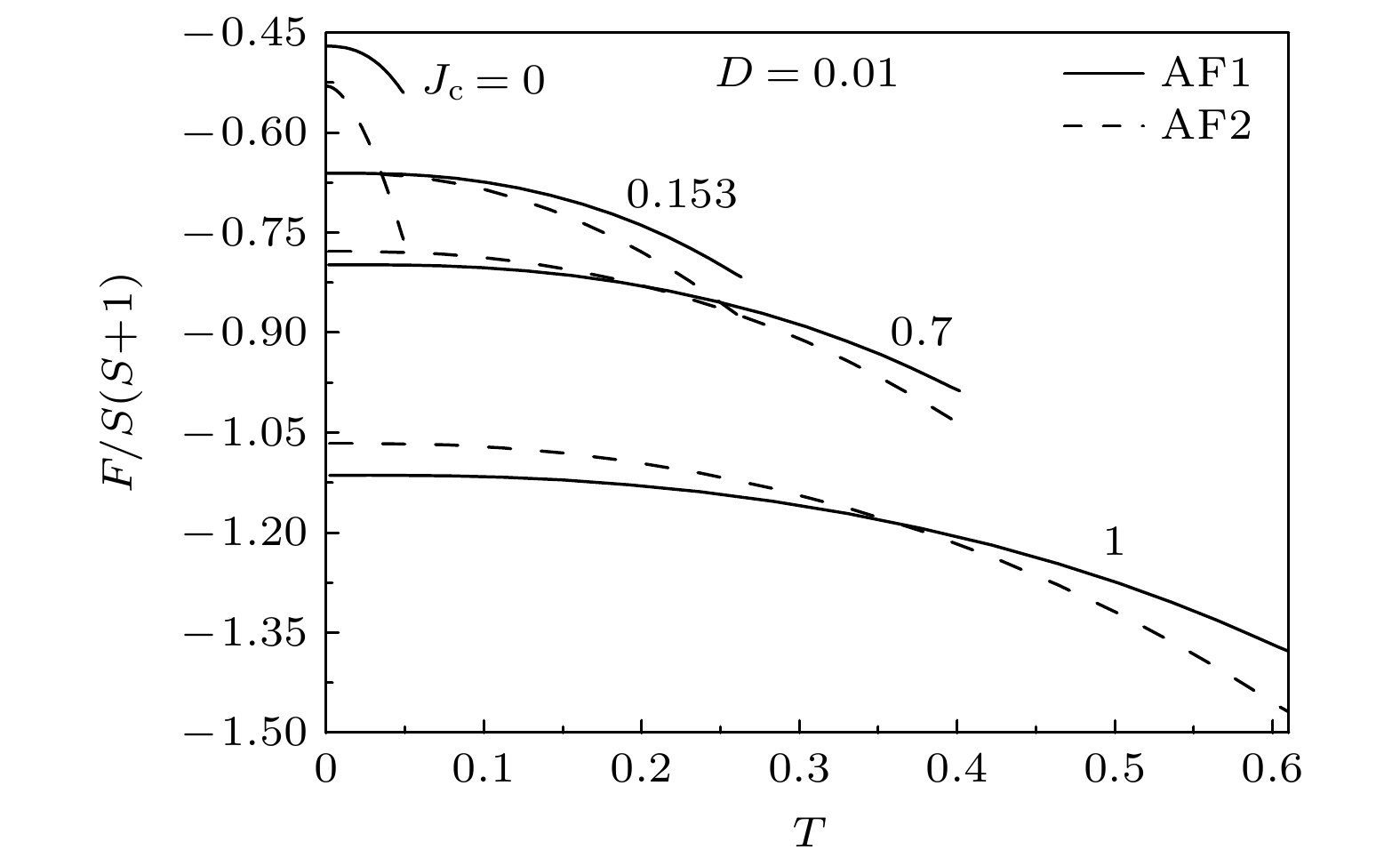
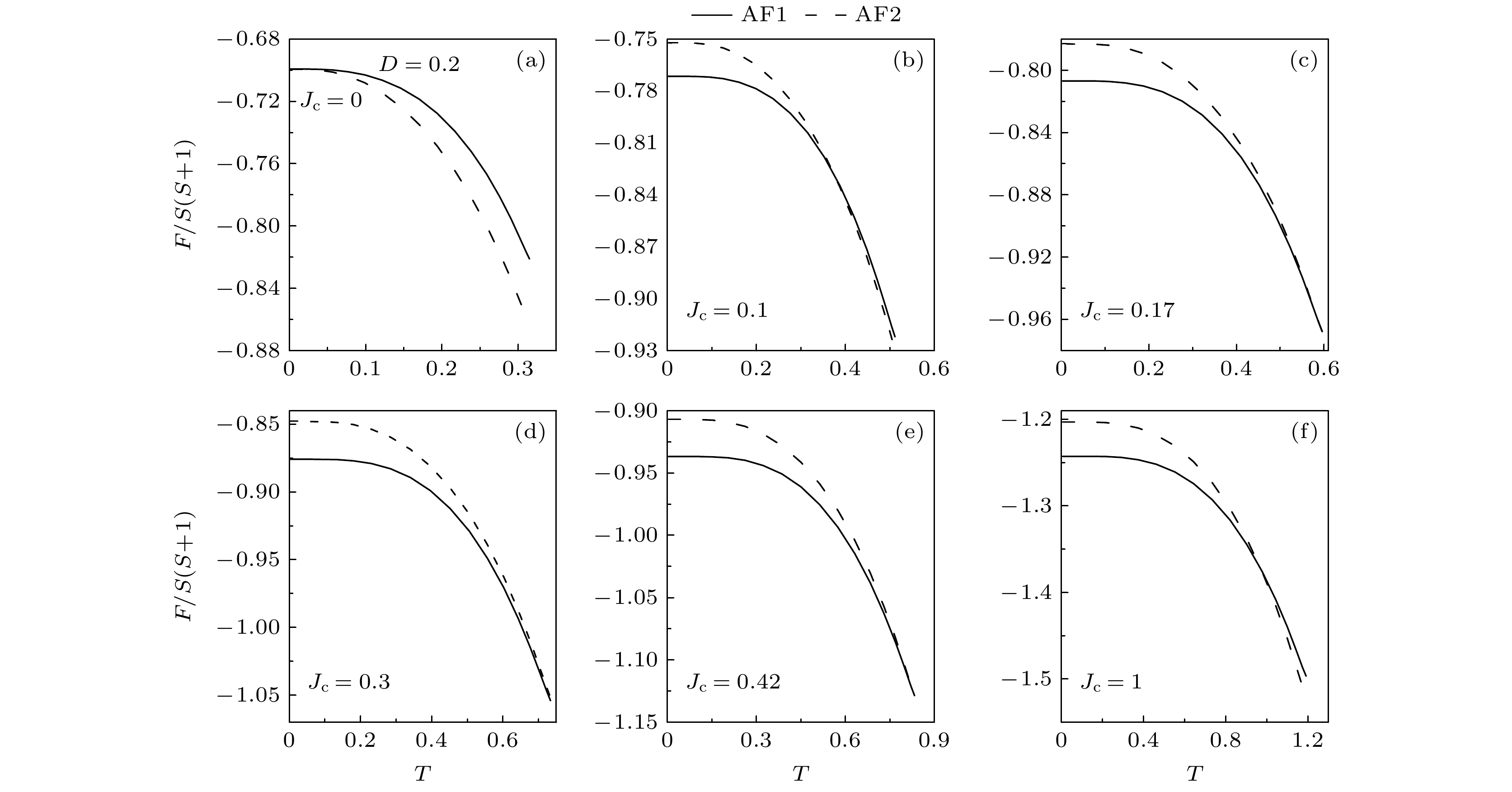
$ D = 0.2 $ 时, 不同$ {J_{\text{c}}} $ 值时的自由能F与温度T之间的变化关系 (a)$ {J_{\text{c}}} = 0 $ ; (b)$ {J_{\text{c}}} = 0.1 $ ; (c)$ {J_{\text{c}}} = 0.17 $ ; (d)$ {J_{\text{c}}} = 0.3 $ ; (e)$ {J_{\text{c}}} = 0.42 $ ; (f)$ {J_{\text{c}}} = 1 $ Figure 4. Free energy F as a function of temperature T for different
$ {J_{\text{c}}} $ values when$ D = 0.2 $ : (a)$ {J_{\text{c}}} = 0 $ ; (b)$ {J_{\text{c}}} = 0.1 $ ; (c)$ {J_{\text{c}}} = 0.17 $ ; (d)$ {J_{\text{c}}} = 0.3 $ ; (e)$ {J_{\text{c}}} = 0.42 $ ; (f)$ {J_{\text{c}}} = 1 $ .
图 5 当
$ {J_2} = 0.5 $ 时, 两个态的自由能在参数${J_{\text{c}}} \text- D$ 空间中大小比较Figure 5. Comparison of the free energies of the two states in the
$ {J_{\text{c}}} $ and D parameter space when$ {J_2} = 0.5 $ .
图 6 当
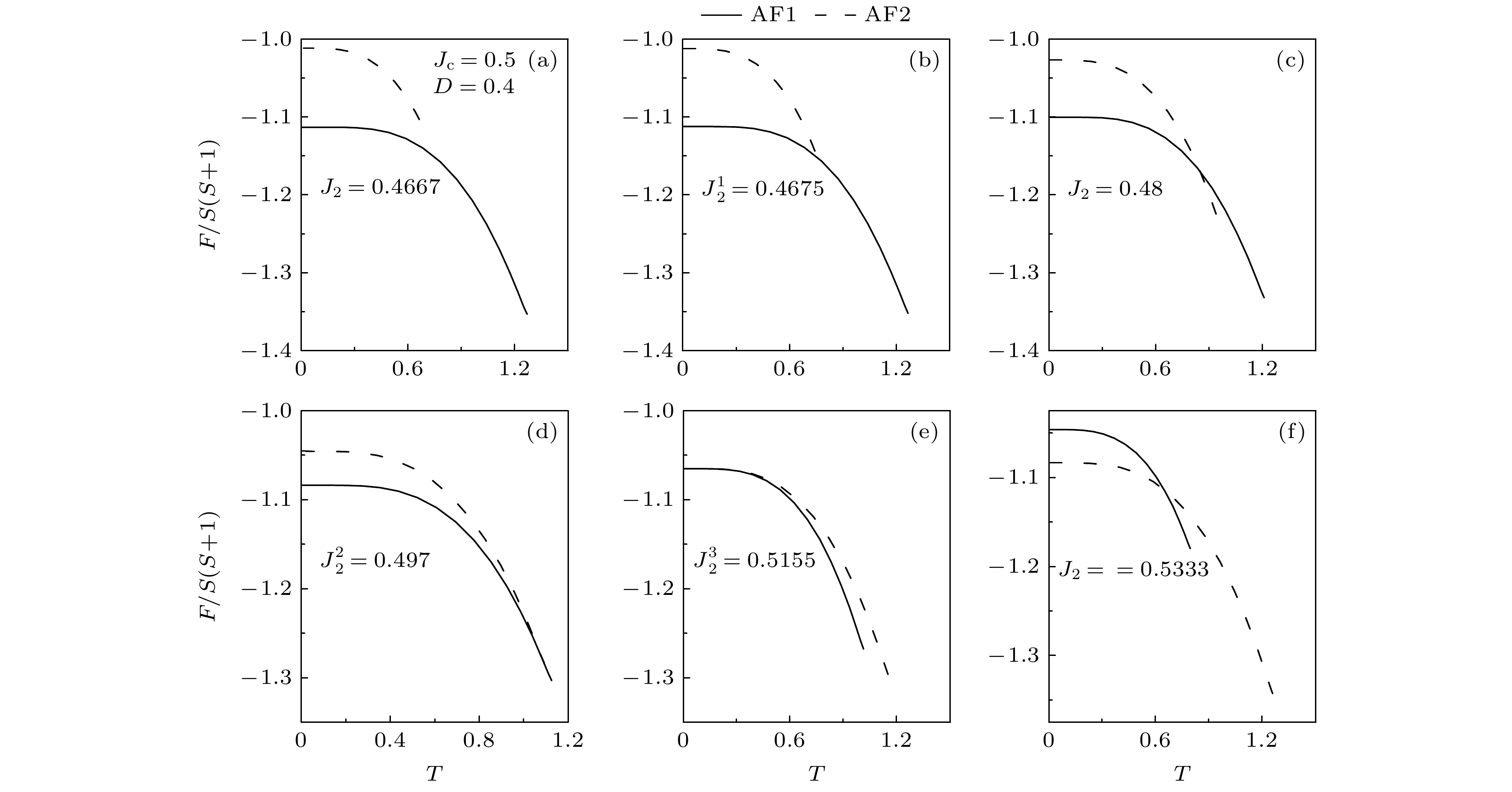
$ {J_{\text{c}}} = 0.5, D = 0.4 $ , 不同$ {J_2} $ 值时的自由能与温度之间的变化关系 (a)$ {J_2} = 0.4667 $ ; (b)$ {J_2} = 0.4675 $ ; (c)$ {J_2} = 0.48 $ ; (d)${J_2} = $ $ 0.4970.497$ ; (e)$ {J_2} = 0.5155 $ ; (f)$ {J_2} = 0.5333 $ Figure 6. Free energy as a function of temperature for different
$ {J_2} $ values when$ {J_{\text{c}}} = 0.5 $ and$ D = 0.4 $ : (a)$ {J_2} = 0.4667 $ ; (b)${J_2} = $ $ 0.4675$ ; (c)$ {J_2} = 0.48 $ ; (d)$ {J_2} = 0.497 $ ; (e)$ {J_2} = 0.5155 $ ; (f)$ {J_2} = 0.5333 $ .
图 7 当
$ {J_{\text{c}}} = - 0.5, D = 0.4 $ 时, 不同$ {J_2} $ 值时的自由能与温度之间的变化关系 (a)$ {J_2} = 0.4667 $ ; (b)$ {J_2} = 0.467 $ ; (c)$ {J_2} = 0.48 $ ; (d)$ {J_2} = 0.4975 $ ; (e)$ {J_2} = 0.5156 $ ; (f)$ {J_2} = 0.5333 $ Figure 7. Free energy as a function of temperature for different
$ {J_2} $ values when$ {J_{\text{c}}} = - 0.5 $ and$ D = 0.4 $ : (a)$ {J_2} = 0.4667 $ ; (b)${J_2} = $ $ 0.467$ ; (c)$ {J_2} = 0.48 $ ; (d)$ {J_2} = 0.4975 $ ; (e)$ {J_2} = 0.5156 $ ; (f)$ {J_2} = 0.5333 $ . -
[1] Manojlović M, Pavkov M, Škrinjar M, PantićM, Kapor D, Stojanović S 2003 Phys. Rev. B 68 014435
Google Scholar
[2] Manojlović M, Pavkov M, Škrinjar M, Pantić M, Kapor D, Stojanović S 2005 Phys. Rev. B 73 132510
[3] Rutonjski M S, Radošević S M, Škrinjar M G, Pavkov-Hrvojević M V, Kapor D V, Pantić M R 2007 Phys. Rev. B 76 172506
[4] Liu G B, Liu B G 2009 J. Phys. :Condens. Matter 21 195701
Google Scholar
[5] Holt M, Sushkov O P, Stanek D, Uhrig G S 2011 Phys. Rev. B 83 144528
Google Scholar
[6] Johnston D C, McQueeney R J, Lake B, Honecker A, Zhitomirsky M E, Nath R, Furukawa Y, Antropov V P, Yogesh Singh 2011 Phys. Rev. B 84 094445
Google Scholar
[7] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[8] Schmalfuß D, Darradi R, Richter J, Schulenburg J, Ihle D 2006 Phys. Rev. Lett. 97 157201
Google Scholar
[9] Nunes W A, J Ricardo de Sousa, J Roberto Viana, Richter J 2010 J. Phys. :Condens. Matter 22 146004
Google Scholar
[10] Nunes W A, Roberto Viana, Ricardo de Sousa J 2011 J. Stat. Mech. ???? 05016
[11] Onofre R, Hamer C J, Oitmaa J 2011 J. Phys. :Condens. Matter 23 416001
Google Scholar
[12] Zhuo F, Jie Q L 2014 Phys. Rev. B 89 054418
Google Scholar
[13] Bishop R F, Li P H Y, Götze O, Richter J 2019 Phys. Rev. B 100 024401
Google Scholar
[14] 王怀玉 2012 凝聚态物理的格林函数理论 (北京: ) 第348页
Wang H Y 2012 Green’s Function in Condensed Matter Physics (Beijing: Alpha Science International Ltd and Science Press) p348 (in Chinese)
[15] Callen H B 1963 Phys. Rev. 130 890
Google Scholar
[16] Anderson F B, Callen H B 1964 Phys. Rev. 136 A1068
Google Scholar
[17] Fröbrich P, Jensen P J, Kuntz P J 2000 Eur. Phys. J. B 13 477
[18] Fröbrich P, Jensen P J, Kuntz P J, Ecker A 2000 Eur. Phys. J. B 18 579
Google Scholar
[19] Fröbrich P, Kuntz P J 2006 Phys. Rep. 432 223
Google Scholar
[20] Wang H Y, Zhai L J, Qian M 2014 J. Magn. Magn. Matter 354 309
Google Scholar
-
[1] Chen Zhao-Liang, Lu Da-Biao, Ye Xu-Bin, Zhao Hao-Ting, Zhang Jie, Pan Zhao, Chi Zhen-Hua, Cui Tian, Shen Yao, Long You-Wen. High-pressure synthesized perovskite-type CeTaN2O and its magnetic and electrical properties. Acta Physica Sinica, 2024, 73(8): 080702. doi: 10.7498/aps.73.20240025 [2] Ren Yan-Ying, Li Ya-Ning, Liu Hong-Sheng, Xu Nan, Guo Kun, Xu Zhao-Hui, Chen Xin, Gao Jun-Feng. Regulation of magnetic moment and magnetic anisotropy of magnetite by doping transition metal elements. Acta Physica Sinica, 2024, 73(6): 066104. doi: 10.7498/aps.73.20231744 [3] Meng Jing, Feng Xin-Wei, Shao Qing-Rong, Zhao Jia-Peng, Xie Ya-Li, He Wei, Zhan Qing-Feng. Magnetic anisotropy and reversal in epitaxial FeGa/IrMn bilayers with different orientations of exchange bias. Acta Physica Sinica, 2022, 71(12): 127501. doi: 10.7498/aps.71.20220166 [4] Qing Yu-Lin, Peng Xiao-Li, Wen Lin, Hu Ai-Yuan. Ground state phase transition of spin-1/2 frustration model on stacked square lattice. Acta Physica Sinica, 2022, 71(3): 037501. doi: 10.7498/aps.71.20211584 [5] Yang Xue, Yang Qing-Hui, Zhang Huai-Wu, Wen Qi-Ye, Bai Fei-Ming, Zhong Zhi-Yong, Zhang Ding, Huang Jian-Tao. Preparation and orientation mechanism analysis of (BiTm)3(GaFe)5O12 magneto-optical single crystal film with out-of-plane orientation. Acta Physica Sinica, 2021, 70(10): 107801. doi: 10.7498/aps.70.20202209 [6] Huang Yu-Hao, Zhang Gui-Tao, Wang Ru-Qian, Chen Qian, Wang Jin-Lan. Electronic structure and stability of two-dimensional bimetallic ferromagnetic semiconductor CrMoI6. Acta Physica Sinica, 2021, 70(20): 207301. doi: 10.7498/aps.70.20210949 [7] . The ground state phase transition of the spin-1/2 frustration model on a stacked square lattice. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211584 [8] Liu Xiang, Mi Wen-Bo. Structure, magnetic and transport properties of Fe3O4 near verwey transition. Acta Physica Sinica, 2020, 69(4): 040505. doi: 10.7498/aps.69.20191763 [9] Fang Yu-Qing, Jin Zuan-Ming, Chen Hai-Yang, Ruan Shun-Yi, Li Ju-Geng, Cao Shi-Xun, Peng Yan, Ma Guo-Hong, Zhu Yi-Ming. Terahertz spectroscopic characterization of spin mode and crystal-field transition in high-throughput grown $ {\bf Sm}_{ x}{\bf Pr}_{ 1– x}{\bf FeO_3} $ crystals. Acta Physica Sinica, 2020, 69(20): 209501. doi: 10.7498/aps.69.20200732[10] Wen Lin, Hu Ai-Yuan. Effect of biquadratic exchange and anisotropy on the critical temperature of antiferromagnet. Acta Physica Sinica, 2020, 69(10): 107501. doi: 10.7498/aps.69.20200077 [11] Jiang Xing-Dong, Guan Xing-Yin, Huang Juan-Juan, Fan Xiao-Long, Xue De-Sheng. Recovering in-plane six-fold magnetic symmetry of epitaxial Fe films by N+ implantation. Acta Physica Sinica, 2019, 68(12): 126102. doi: 10.7498/aps.68.20190131 [12] Xiao Jia-Xing, Lu Jun, Zhu Li-Jun, Zhao Jian-Hua. Perpendicular magnetic properties of ultrathin L10-Mn1.67Ga films grown by molecular-beam epitaxy. Acta Physica Sinica, 2016, 65(11): 118105. doi: 10.7498/aps.65.118105 [13] Hu Ni, Liu Yong, Tang Wu-Feng, Pei Ling, Fang Peng-Fei, Xiong Rui, Shi Jing. Fe/Cr doping effects on the magnetism in charge-ordered manganite La0.4Ca0.6MnO3. Acta Physica Sinica, 2014, 63(23): 237502. doi: 10.7498/aps.63.237502 [14] Chen Jia-Luo, Di Guo-Qing. Influence of magnetic anisotropy thermoelectric effect on spin-dependent devices. Acta Physica Sinica, 2012, 61(20): 207201. doi: 10.7498/aps.61.207201 [15] Hu Ni, Liu Yong, Cheng Li, Shi Jing, Xiong Rui. Mn-site Fe/Cr doping effects in charge-ordered antiferromagnetic manganite La0.4Ca0.6MnO3. Acta Physica Sinica, 2011, 60(1): 017503. doi: 10.7498/aps.60.017503 [16] Zhang Hui, Zeng De-Chang. The inverse magnetostrictive effect in Tb0.3Dy0.7Fe2. Acta Physica Sinica, 2010, 59(4): 2808-2814. doi: 10.7498/aps.59.2808 [17] Han Jiu-Rong, Jiang Xue-Fan, Liu Xian-Feng. First-principles studies of helical-spin order in frustrated triangular antiferromagnet AgCrO2. Acta Physica Sinica, 2010, 59(9): 6487-6493. doi: 10.7498/aps.59.6487 [18] Ao Qi, Zhang Wa-Li, Zhang Yi, Wu Jian-Sheng. Nanostructure and hard magnetic properties of exchange coupled Nd-Fe-B/FeCo multilayer films. Acta Physica Sinica, 2007, 56(2): 1135-1140. doi: 10.7498/aps.56.1135 [19] Guo Yu-Xian, Wang Jie, Xu Peng-Shou, Li Hong-Hong, Cai Jian-Wang. Element-specific in-plane magnetic anisotropy in Co0.9Fe0.1 films. Acta Physica Sinica, 2007, 56(2): 1121-1126. doi: 10.7498/aps.56.1121 [20] Li Rui-Peng, Wang Jie, Li Hong-Hong, Guo Yu-Xian, Wang Feng, Hu Zhi-Wei. In-plane anisotropy of iron single-crystal thin film using x-ray magnetic circular dichroism. Acta Physica Sinica, 2005, 54(8): 3851-3855. doi: 10.7498/aps.54.3851
DownLoad:
Catalog
Metrics
- Abstract views: 4171
- PDF Downloads: 49
- Cited By: 0
