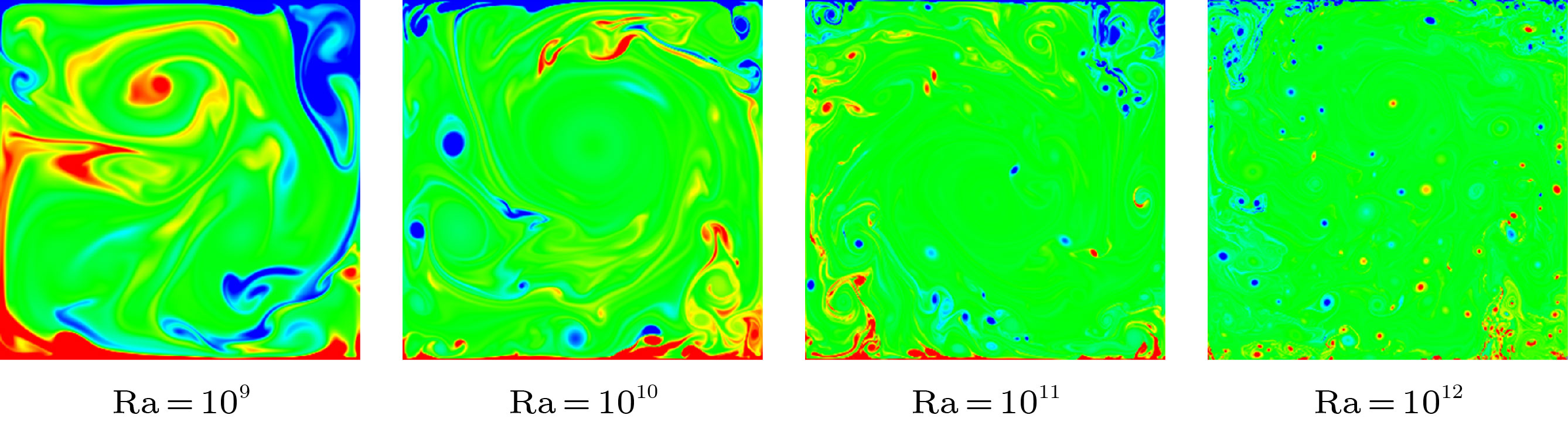
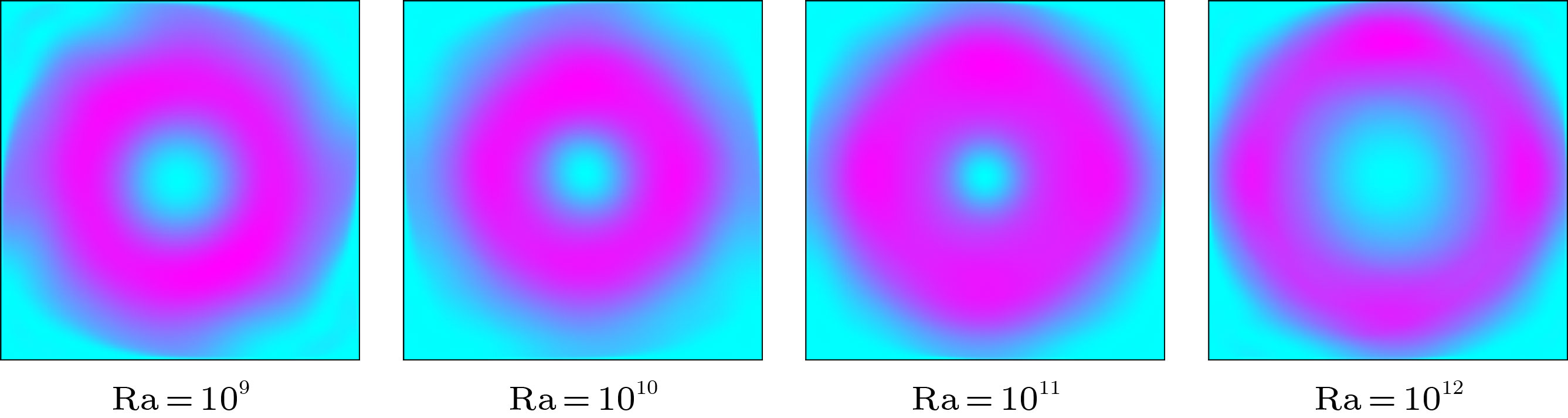
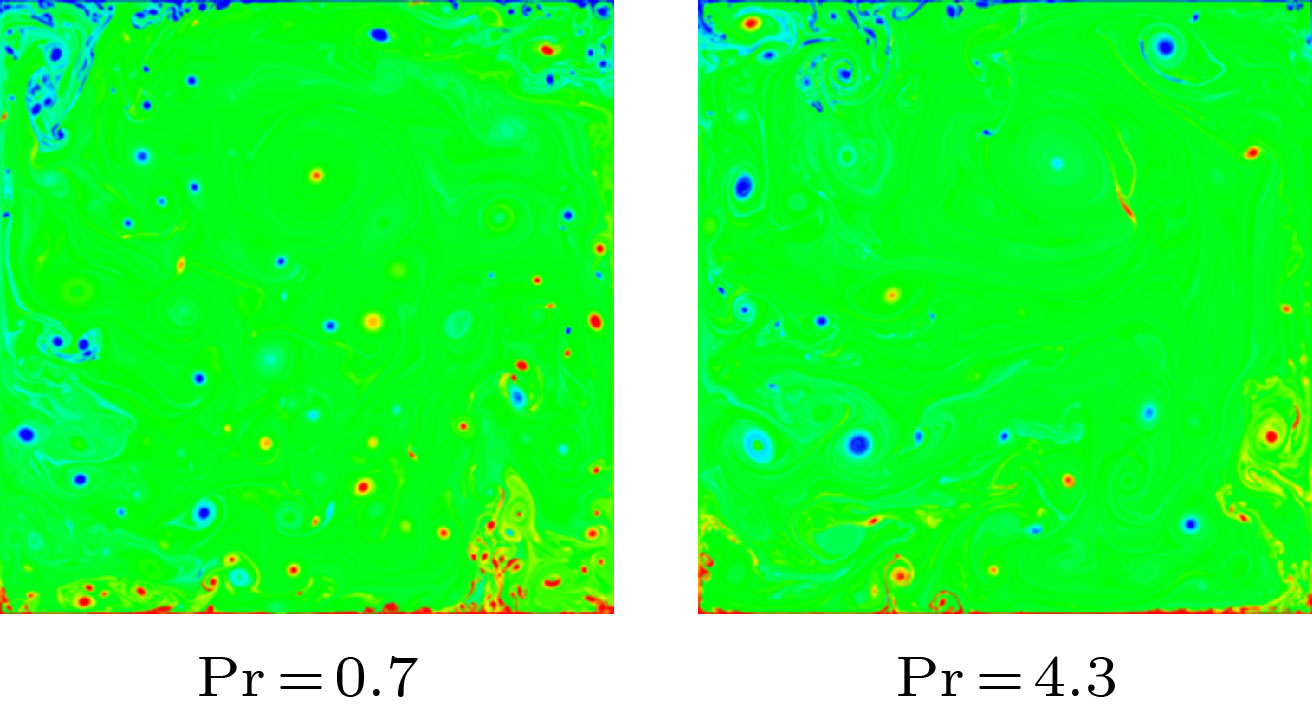
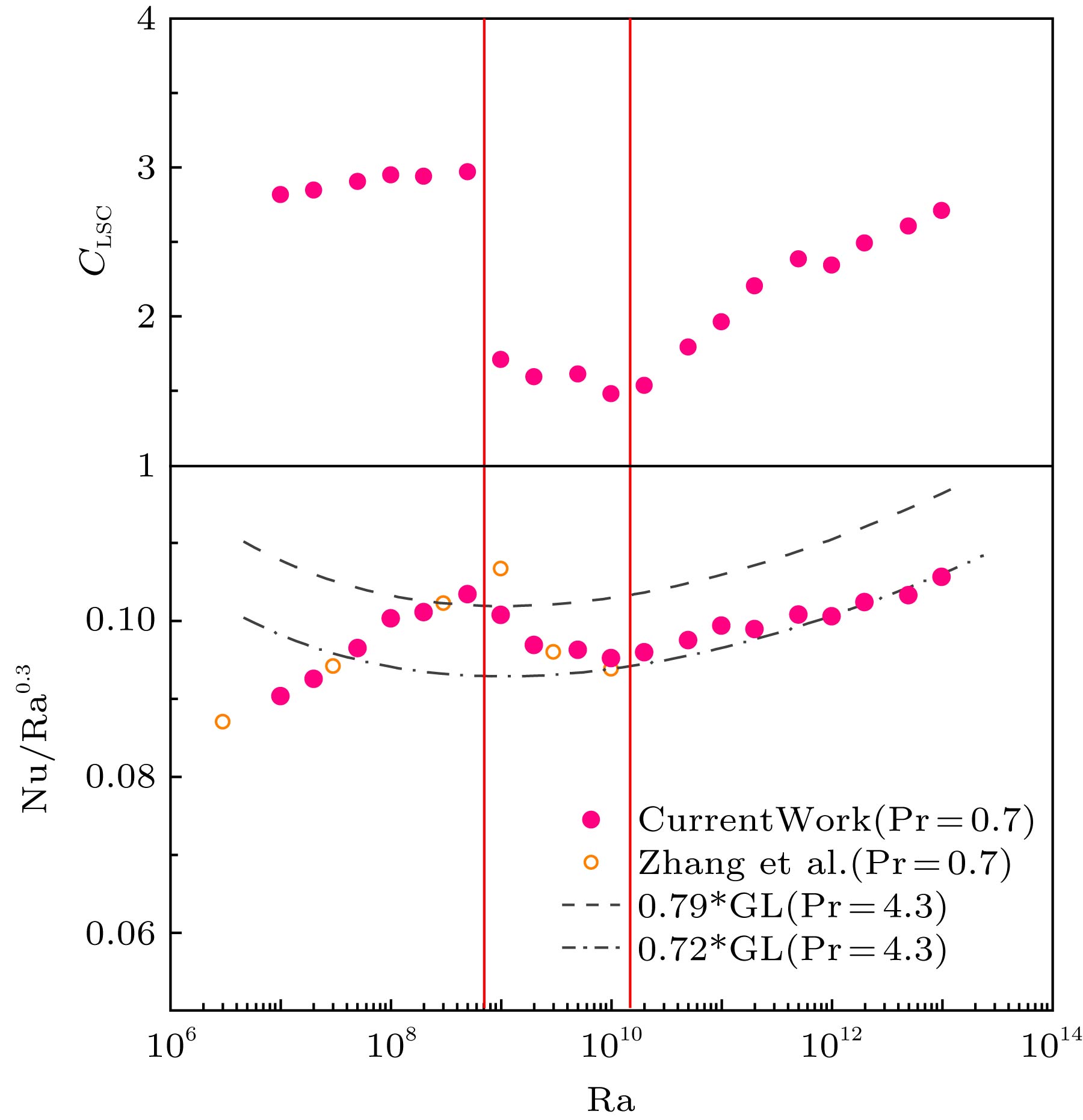
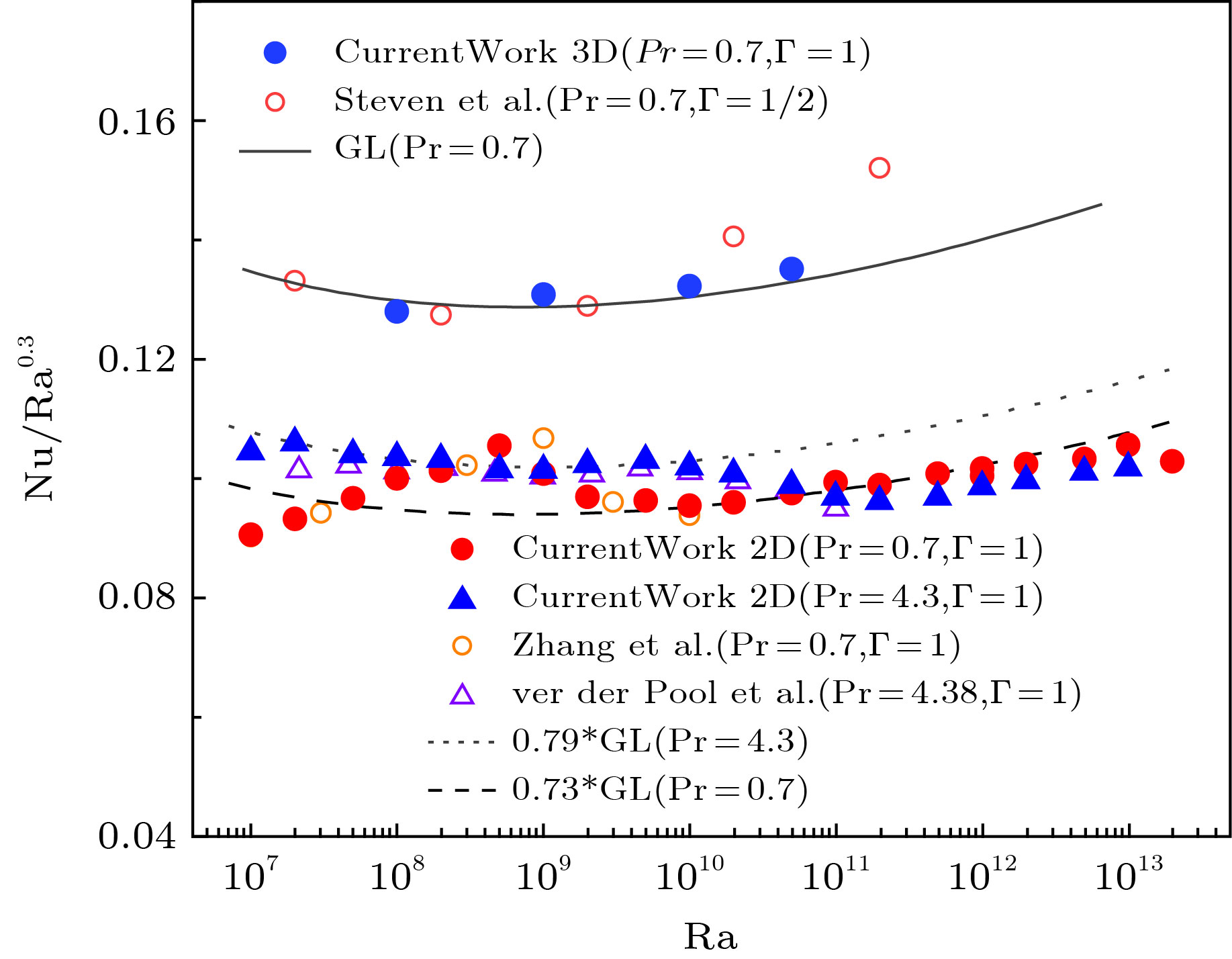
-
The Grossman and Lohse (GL) theory is an important theory for studying the heat transfer characteristics of the turbulent convection. Previous computational studies have found that when the Ra number is higher than a certain value, the change of the heat transfer Nu number with Ra number in two-dimensional turbulent thermal convection is different from that in the three-dimensional thermal convection, deviating from the multiples line of the GL theory prediction. Therefore, the value of studying the two-dimensional numerical calculation of turbulent thermal convection with high Ra number is questioned. The numerical calculations of a series of two-dimensional turbulent thermal convection events with high and very high Ra number(specifically, maximum Ra = 1013 with Pr = 0.7 and 4.3) are carried out in this paper. The results show that there exists a good correlation between the heat transfer Nu number and the variation of large scale circulation path length(that reflects the plume motion) with Ra number in the two-dimensional turbulent convection, and they have two Ra number transition points. The first transition point appears in the large scale circulation from the ellipse to the circle, when its circumference CLSC of the large scale circulation suddenly decreases with Ra number increasing. The second transition point appears at the minimum circumference CLSC, and then the plume rheology becomes vortex group and the circumference CLSC increases with Ra number increasing. The Ra number at transition point for a smaller Pr number is lower. The variation of the heat transfer Nu number after Ra0.3 compensation shows that the local scale law of Nu number decreases as the circumference CLSC of the large scale circulation becomes small, and a phenomenon of deviating from the multiples line of GL theory prediction appears. When Ra number is higher than the second transition point, the local scale law of the Nu number varying with Ra number is in good agreement with the multiples line of GL theory prediction again in 2D turbulent thermal convection. It means that the numerical results of two-dimensional turbulent thermal convection can correctly reflect the heat transfer characteristics of turbulent thermal convection under the condition of very high Ra number.
-
Keywords:
- 2D turbulent convection /
- heat transfer characteristics /
- large scale circulation path circumference /
- very high Ra number /
- Grossman and Lohse theory
[1] Ahlers G, Grossmann S, Lohse D 2009 Rev. Mod. Phys. 81 503
Google Scholar
[2] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[3] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[4] He X, van Gils D P M, Bodenschatz E, Ahlers G 2015 New J. Phys. 17 63028
Google Scholar
[5] Zhou Q, Xia K Q 2010 Phys. Rev. Lett. 104 104301
Google Scholar
[6] Stevens R J A M, Lohse D, Verzicoo R 2011 J. Fluid Mech. 688 31
Google Scholar
[7] Zhu X, Mathai V, Stevens R J A M, et al. 2018 Phys. Rev. Lett. 120 144502
Google Scholar
[8] Stevens R J A M, Blass A, Zhu X J 2018 Phys. Rev. Fluids 3 04150
[9] 黄茂静, 包芸 2016 65 204702
Google Scholar
Huang M J, Bao Y 2016 Acta Phys. Sin. 65 204702
Google Scholar
[10] 包芸, 高振源, 叶孟翔 2018 67 104701
Bao Y, Gao Z Y, Ye M X 2018 Acta Phys. Sin. 67 104701
[11] Bao Y, Chen J, Liu B F, et al. 2015 J. Fluid Mech. 784 R5
Google Scholar
[12] Chen J, Bao Y, Yin Z X, et al. 2017 Int. J. Heat Mass Transfer 115 556
Google Scholar
[13] 林泽鹏, 包芸 2018 中国科学: 物理学力学天文学 48 054702
Lin Z P, Bao Y 2018 Sci. Sin.Phys. Mech. Astron. 48 054702
[14] 林泽鹏, 包芸 2018 中国科学: 物理学力学天文学 48 104702
Lin Z P, Bao Y 2018 Sci. Sin.Phys. Mech. Astron. 48 104702
[15] Shishkina O, Horn S, Wagner S, et al. 2015 Phys. Rev. Lett 114 114302
Google Scholar
[16] 何鹏, 黄茂静, 包芸 2018 中国科学: 物理学力学天文学 48 124702
He P, Huang M J, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 124702
[17] Gao Z Y, Luo J H, Bao Y 2018 Chin. Phys. B 27 104702
Google Scholar
[18] van der Poel E P, Stevens R J A M, Lohse D 2013 J. Fluid Mech. 736 177
Google Scholar
[19] Bao Y, Luo J H, Ye M X 2018 J. Mech. 34 159
Google Scholar
[20] Stevens RJAM, van der Poel E P, Grossmann S, et al. 2013 J. Fluid Mech. 730 295
Google Scholar
[21] Zhang Y, Huang Y X, Jiang N, et al. 2017 Phys. Rev. E 96 023105
Google Scholar
[22] Sun C, Xia K Q 2005 Phys. Rev. E 72 067302
Google Scholar
-
图 1 热对流传热Nu数随Ra数的变化情况
Figure 1. The variation of the Nu number with Ra number for the turbulent convection.
图 2 Pr = 0.7典型Ra数的二维热对流瞬时温度场
Figure 2. The instantaneous temperature fields with typical Ra number at Pr = 0.7.
图 3 Pr = 0.7典型Ra数的二维热对流平均温度场和流线图
Figure 3. The average temperature fields and stream lines with typical Ra number at Pr = 0.7.
图 4 Pr = 0.7典型Ra数的平均速度场分布
Figure 4. The average velocity field distributions with typical Ra number at Pr = 0.7.
图 5 Ra = 1012时不同Pr数的瞬时温度场及羽流结构
Figure 5. The instantaneous temperature field and plume structure with different Pr number at Ra = 1012.
图 6 Pr = 0.7时大尺度环流路径图
Figure 6. The large scale circulation path at Pr = 0.7.
图 7 大尺度环流路径周长与传热Nu数随Ra变化及其相关性, Pr = 0.7
Figure 7. The variation of large scale circulation path length and Nu number with Ra and its correlation at Pr = 0.7.
图 8 大尺度环流路径周长与传热Nu数随Ra变化及其相关性, Pr = 4.3
Figure 8. The variation of large scale circulation path and Nu number with Ra and its correlation at Pr = 4.3.
表 1 计算Ra数
Table 1. The Ra numbers.
Ra 107, 2×107, 5×107, 108, 2×108, 5×108, 109, 2×109, 5×109, 1010, 2×1010, 5×1010, 1011, 5×1011, 1012, 2×1012, 1013 
DownLoad: CSV
-
[1] Ahlers G, Grossmann S, Lohse D 2009 Rev. Mod. Phys. 81 503
Google Scholar
[2] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[3] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[4] He X, van Gils D P M, Bodenschatz E, Ahlers G 2015 New J. Phys. 17 63028
Google Scholar
[5] Zhou Q, Xia K Q 2010 Phys. Rev. Lett. 104 104301
Google Scholar
[6] Stevens R J A M, Lohse D, Verzicoo R 2011 J. Fluid Mech. 688 31
Google Scholar
[7] Zhu X, Mathai V, Stevens R J A M, et al. 2018 Phys. Rev. Lett. 120 144502
Google Scholar
[8] Stevens R J A M, Blass A, Zhu X J 2018 Phys. Rev. Fluids 3 04150
[9] 黄茂静, 包芸 2016 65 204702
Google Scholar
Huang M J, Bao Y 2016 Acta Phys. Sin. 65 204702
Google Scholar
[10] 包芸, 高振源, 叶孟翔 2018 67 104701
Bao Y, Gao Z Y, Ye M X 2018 Acta Phys. Sin. 67 104701
[11] Bao Y, Chen J, Liu B F, et al. 2015 J. Fluid Mech. 784 R5
Google Scholar
[12] Chen J, Bao Y, Yin Z X, et al. 2017 Int. J. Heat Mass Transfer 115 556
Google Scholar
[13] 林泽鹏, 包芸 2018 中国科学: 物理学力学天文学 48 054702
Lin Z P, Bao Y 2018 Sci. Sin.Phys. Mech. Astron. 48 054702
[14] 林泽鹏, 包芸 2018 中国科学: 物理学力学天文学 48 104702
Lin Z P, Bao Y 2018 Sci. Sin.Phys. Mech. Astron. 48 104702
[15] Shishkina O, Horn S, Wagner S, et al. 2015 Phys. Rev. Lett 114 114302
Google Scholar
[16] 何鹏, 黄茂静, 包芸 2018 中国科学: 物理学力学天文学 48 124702
He P, Huang M J, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 124702
[17] Gao Z Y, Luo J H, Bao Y 2018 Chin. Phys. B 27 104702
Google Scholar
[18] van der Poel E P, Stevens R J A M, Lohse D 2013 J. Fluid Mech. 736 177
Google Scholar
[19] Bao Y, Luo J H, Ye M X 2018 J. Mech. 34 159
Google Scholar
[20] Stevens RJAM, van der Poel E P, Grossmann S, et al. 2013 J. Fluid Mech. 730 295
Google Scholar
[21] Zhang Y, Huang Y X, Jiang N, et al. 2017 Phys. Rev. E 96 023105
Google Scholar
[22] Sun C, Xia K Q 2005 Phys. Rev. E 72 067302
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7718
- PDF Downloads: 64
- Cited By: 0
