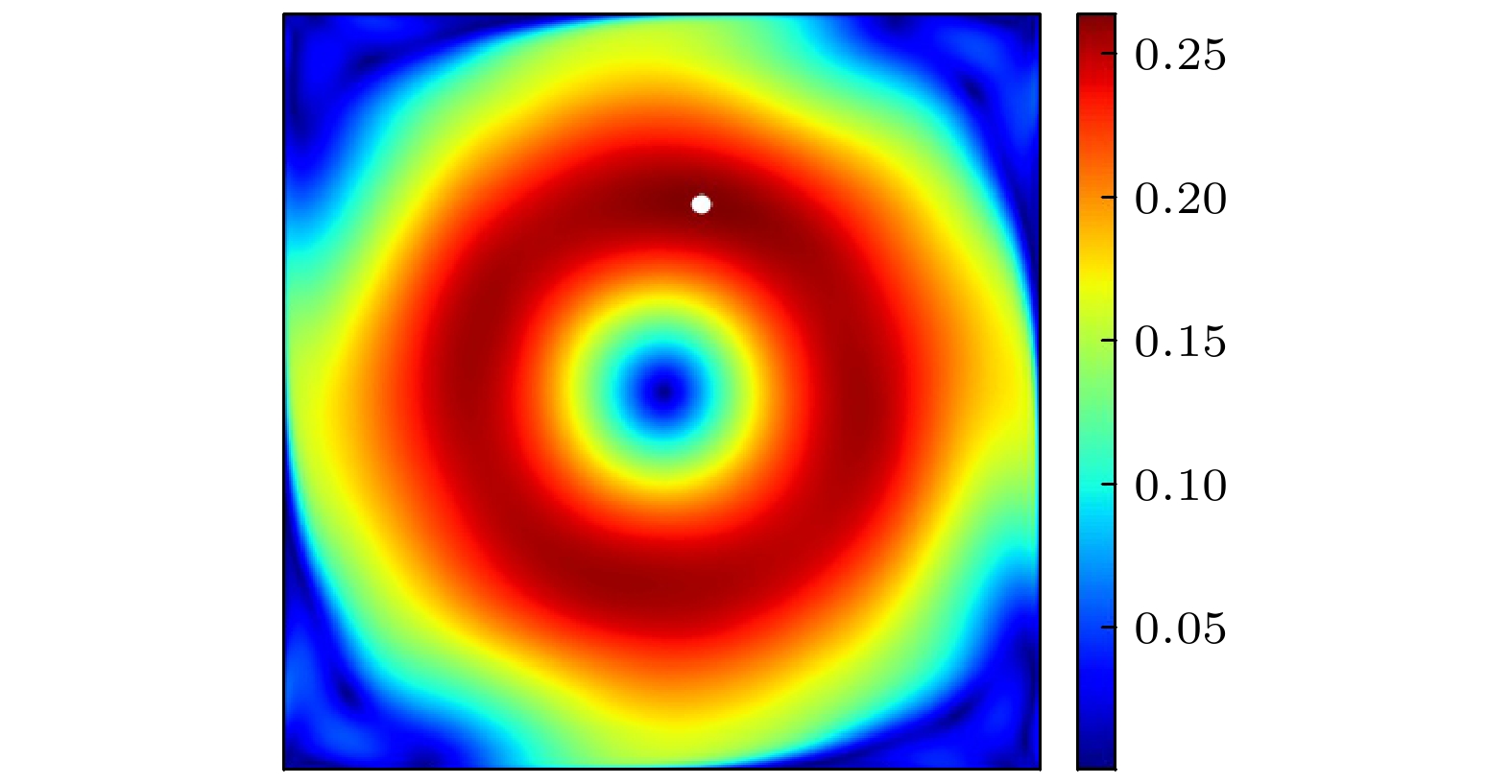
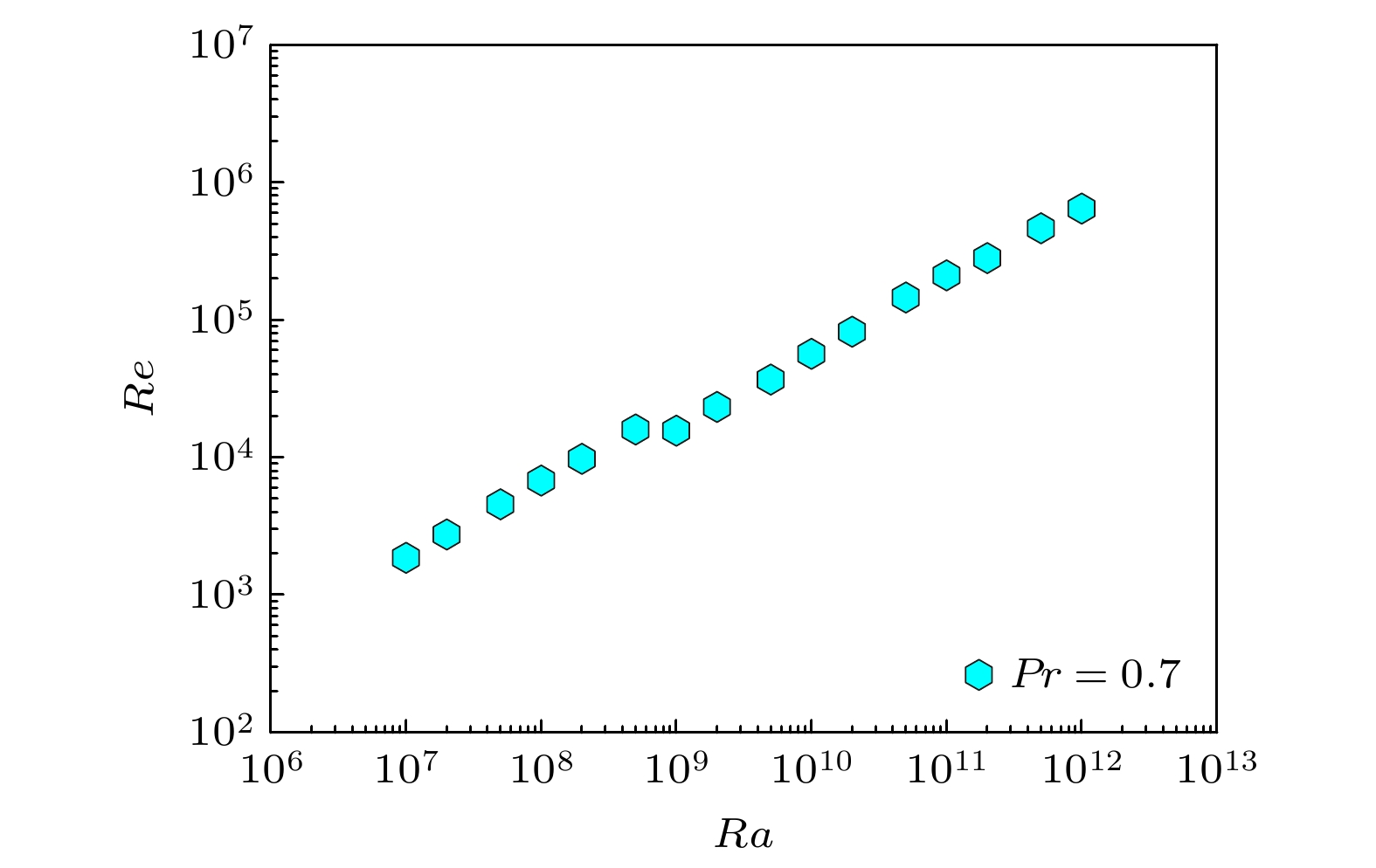
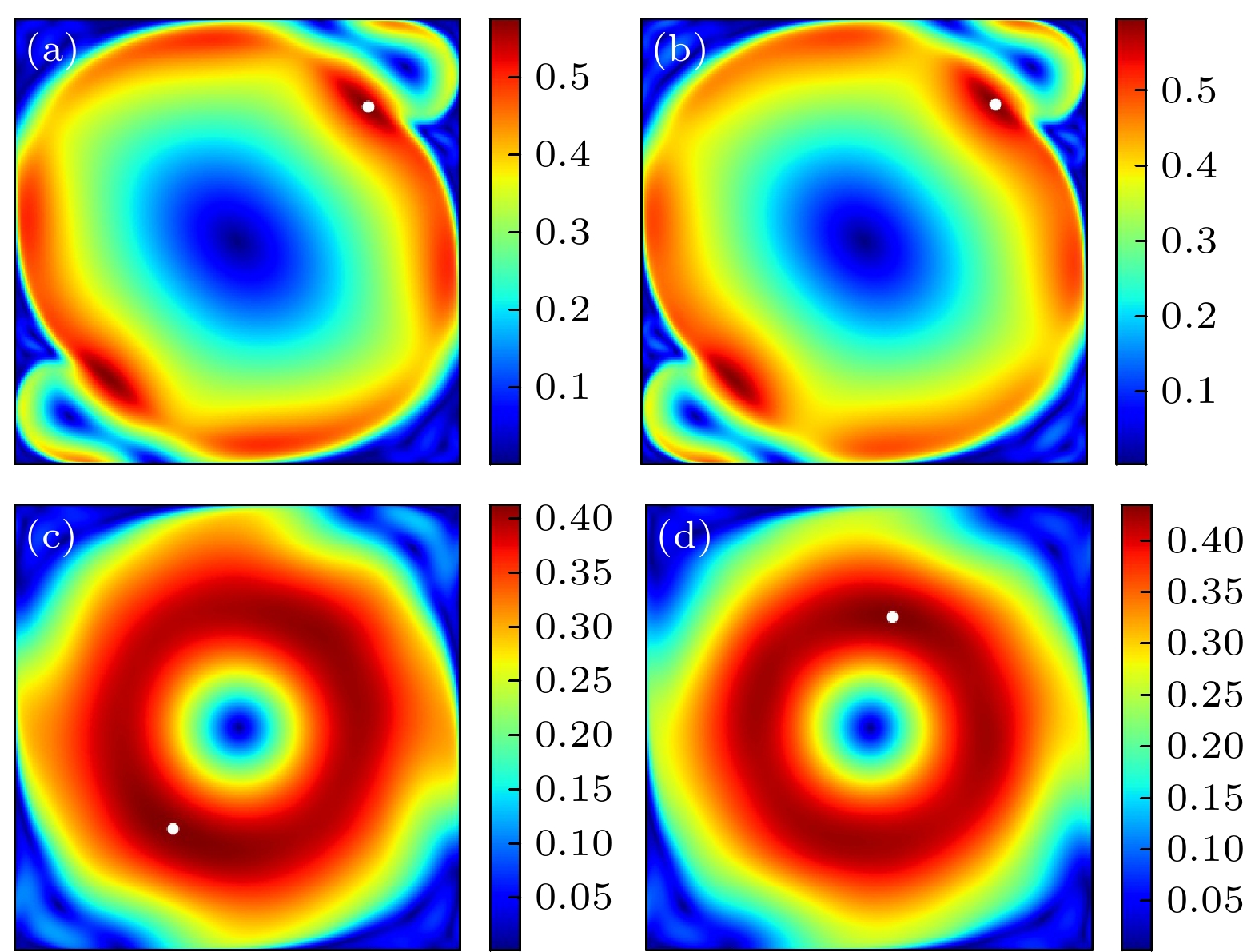
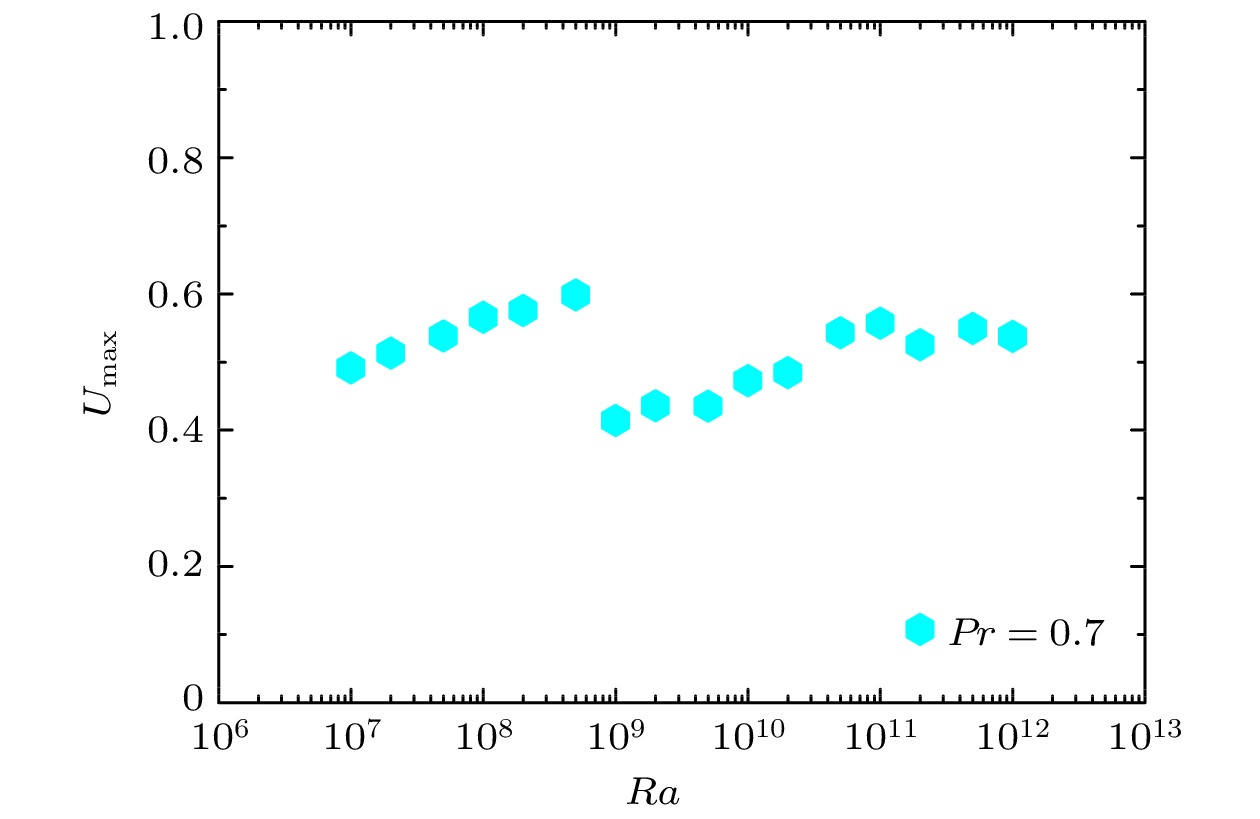
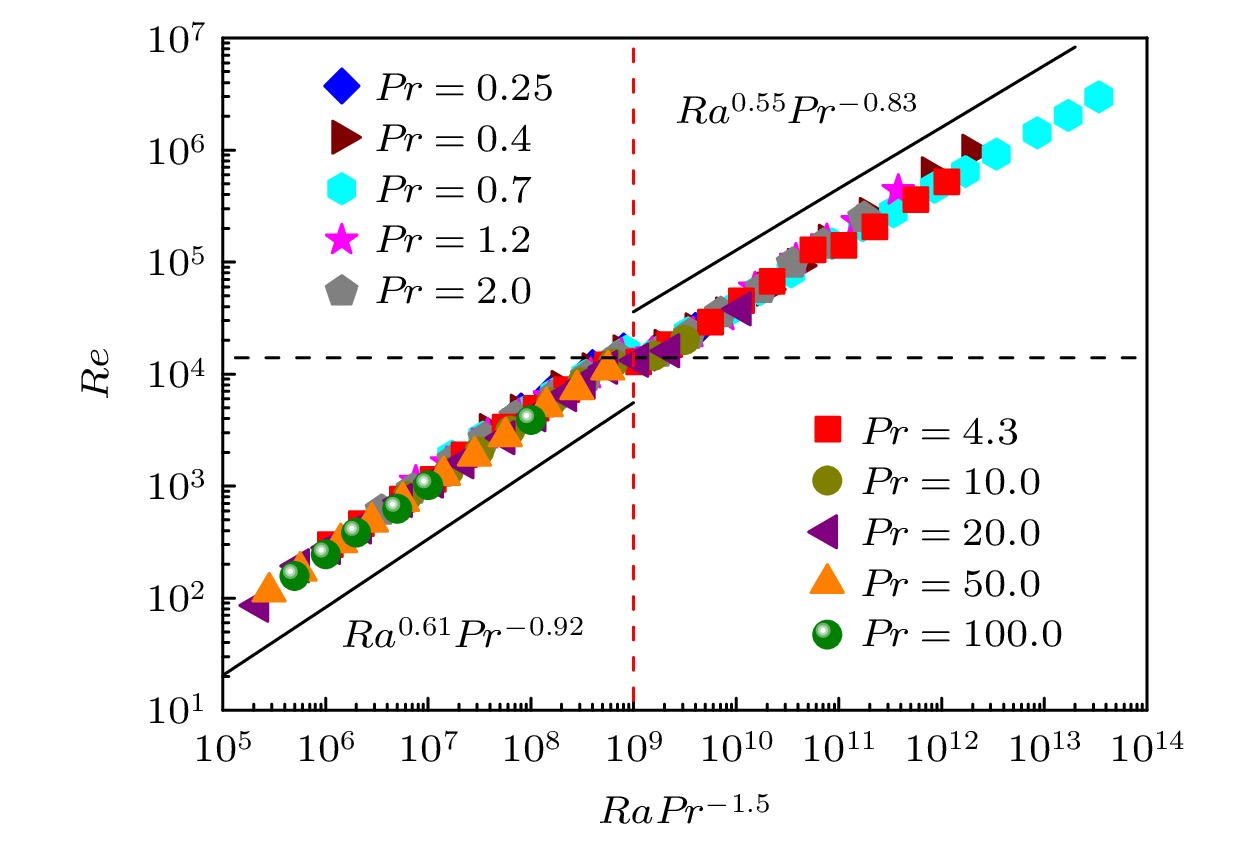
-
Rayleigh number (Ra) dependence in Rayleigh-Bénard (RB) convection has been studied by many investigators, but the reported power-law scaling expressions are different in these researches. Previous studies have found that when Ra reaches a critical value, the flow patterns change and a transition appears in the scaling of Nu(Ra) (where Nu represents Nusselt number) and Re(Ra) (where Re denotes Reynold number). The Grossmann-Lohse(GL) model divides the Ra-Pr(where Pr refers to Prandtl number) phase into several regions to predict the scaling expressions of Nu(Ra,Pr) and Re(Ra,Pr), indicating that the thermal dissipation behavior and kinetic dissipation behaviors are diverse in the different regions. Moreover, some physical quantities also show a transition and some structures in the flow fields, such as large scale circulation and boundary layer, change when Ra increases. In this work, we conduct a series of numerical simulations in two-dimensional RB convection with Ra ranging from 107 to 1012 and Pr ranging from 0.25 to 100, which is unprecedentedly wide. The relationship between the maximum velocity and Ra is investigated, and an unexpected drop happens when Ra reaches a critical value Rac, and Rac increases with Pr increasing. The Re number, which is defined as a maximum velocity, also shows a plateau at Rac. Before and after Rac, the Ra scaling exponent of Re remains 0.55, which gets smaller at very high Ra. Specially, under different Pr values, the plateau appears at Rec ≈ 1.4 × 104. In addition, a scaling Rac~Pr1.5 is found and the Ra is compensated for by Pr–1.5 to disscuss the relationship between Re and RaPr–1.5. It is interesting that the Re(RaPr–1.5) expressons at different Pr values well coincide, indicating a self-similarity of Re(RaPr–1.5). The plateau appears at RaPr–1.5 = 1 × 109, meaning that Rec would reach 1.4 × 104 at any Pr value when RaPr–1.5 = 1 × 109. To further investigate the plateau of Re, the flow patterns are compared with time-averaged velocity fields and we find that the large scale circulation (LSC) changes from ellipse to circle at Rac. In other words, the flow pattern will change into circular LSC at Rec at different Pr values, and Rec is a constant as mentioned above. This finding can help us to distinguish the two flow patterns with given Ra and Pr, and to predict the Re scaling in an appropriate range of Ra with different Pr values.
-
Keywords:
- thermal convection /
- Reynolds number /
- flow pattern /
- Prandtl number
[1] Malkus W V R 1954 Proc. R. Soc. Lond. A 225 196
Google Scholar
[2] Globe S, Dropkin D 1959 J. Heat Transfer 81 24
Google Scholar
[3] Shraiman B I, Siggia E D 1990 Phys. Rev. A 42 3650
Google Scholar
[4] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[5] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[6] Grossmann S, Lohse D 2002 Phys. Rev. E 66 016305
Google Scholar
[7] Grossmann S, Lohse D 2004 Phys. Fluids 16 4462
Google Scholar
[8] Stevens R J A M, Van Der Poel E P, Grossmann S, Lohse D 2013 J. Fluid Mech. 730 295
Google Scholar
[9] Xia K Q, Lam S, Zhou S Q 2002 Phys. Rev. Lett. 88 064501
Google Scholar
[10] van der Poel E P, Stevens R J A M, Lohse D 2013 J. Fluid Mech. 736 177
Google Scholar
[11] Khurana A 1988 Phys. Today 41 17
Google Scholar
[12] Willis G E, Deardorff J W 1970 J. Fluid Mech. 44 661
Google Scholar
[13] Krishnamurti R 1970 J. Fluid Mech. 42 309
Google Scholar
[14] Ahlers G 1974 Phys. Rev. Lett. 33 1185
Google Scholar
[15] McLaughlin J B, Martin P C 1974 Phys. Rev. Lett. 33 1189
Google Scholar
[16] Heslot F, Castaing B, Libchaber A 1987 Phys. Rev. A 36 5870
Google Scholar
[17] Castaing B, Gunaratne G, Heslot F, Kadanoff L, Libchaber A, Thomae S, Wu X Z, Zaleski S, Zanetti G 1989 J. Fluid Mech. 204 1
Google Scholar
[18] Sano M, Wu X Z, Libchaber A 1989 Phys. Rev. A 40 6421
Google Scholar
[19] 包芸, 何建超, 高振源 2019 68 164701
Google Scholar
Bao Y, He J C, Gao Z Y 2019 Acta Phys. Sin. 68 164701
Google Scholar
[20] Gao Z Y, Luo J H, Bao Y 2018 Chin. Phys. B 27 104702
Google Scholar
[21] Verzicco R, Camuss I R 1999 J. Fluid Mech. 383 55
Google Scholar
[22] Kerr R M 1996 J. Fluid Mech. 310 139
Google Scholar
[23] Li X M, He J D, Tian Y, Hao P, Huang S D 2021 J. Fluid Mech. 915 A60
Google Scholar
[24] Chen X, Huang S D, Xia K Q, Xi H D 2019 J. Fluid Mech. 877 R1
Google Scholar
[25] Xu A, Chen X, Xi H D 2021 Phys. Fluids 910 A33
Google Scholar
[26] Werne J, Deluca EE, Rosner R, Cattaneo F 1991 Phys. Rev. Lett. 67 3919
Google Scholar
[27] Bao Y, Luo J H, Ye M X 2017 J. Mech. 34 159
Google Scholar
[28] Sun X H 1995 Parallel Comput. 21 1241
Google Scholar
[29] Shishkina O, Stevens R J A M, Grossmann S, Lohse D 2010 New J. Phys. 12 075022
Google Scholar
[30] He J C, Fang M W, Gao Z Y, Huang S D, Bao Y 2021 Chin. Phys. B 30 094701
Google Scholar
[31] Gao Z Y, Bao Y, Huang S D 2019 72nd Annual Meeting of the APS Division of Fluid Dynamics Seattle, Washington, November 23–26, G14.00003
-
图 1 二维热对流计算算例Ra-Pr相图
Figure 1. The Ra-Pr Phase diagram explored in the present study.
图 2 平均速度分布及最大速度点
Figure 2. The time-averaged velocity filed and the maximum velocity point.
图 3 Re数与Ra数关系
Figure 3. Re as a function of Ra
图 4 平均速度场变化及流态突变(Pr = 0.7) (a) Ra = 2 × 108; (b) Ra = 5 × 108; (c) Ra = 1 × 109; (d) Ra = 2 × 109
Figure 4. The time-averaged velocity fieldsc and the sudden change of flow pattern (Pr = 0.7): (a) Ra = 2 × 108; (b) Ra = 5 × 108; (c) Ra = 1 × 109; (d) Ra = 2 × 109.
图 5 最大速度随Ra数变化
Figure 5. The maximum velocity as a function of Ra
图 6 Re数与Ra的关系图
Figure 6. Re as a function of Ra
图 7 不同Pr数下Re数与Ra数的关系
Figure 7. Re as a function of Ra at different Pr
图 8 不同Pr数下Re数与RaPr–1.5的关系
Figure 8. Re as a function of RaPr–1.5 at different Pr
-
[1] Malkus W V R 1954 Proc. R. Soc. Lond. A 225 196
Google Scholar
[2] Globe S, Dropkin D 1959 J. Heat Transfer 81 24
Google Scholar
[3] Shraiman B I, Siggia E D 1990 Phys. Rev. A 42 3650
Google Scholar
[4] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[5] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[6] Grossmann S, Lohse D 2002 Phys. Rev. E 66 016305
Google Scholar
[7] Grossmann S, Lohse D 2004 Phys. Fluids 16 4462
Google Scholar
[8] Stevens R J A M, Van Der Poel E P, Grossmann S, Lohse D 2013 J. Fluid Mech. 730 295
Google Scholar
[9] Xia K Q, Lam S, Zhou S Q 2002 Phys. Rev. Lett. 88 064501
Google Scholar
[10] van der Poel E P, Stevens R J A M, Lohse D 2013 J. Fluid Mech. 736 177
Google Scholar
[11] Khurana A 1988 Phys. Today 41 17
Google Scholar
[12] Willis G E, Deardorff J W 1970 J. Fluid Mech. 44 661
Google Scholar
[13] Krishnamurti R 1970 J. Fluid Mech. 42 309
Google Scholar
[14] Ahlers G 1974 Phys. Rev. Lett. 33 1185
Google Scholar
[15] McLaughlin J B, Martin P C 1974 Phys. Rev. Lett. 33 1189
Google Scholar
[16] Heslot F, Castaing B, Libchaber A 1987 Phys. Rev. A 36 5870
Google Scholar
[17] Castaing B, Gunaratne G, Heslot F, Kadanoff L, Libchaber A, Thomae S, Wu X Z, Zaleski S, Zanetti G 1989 J. Fluid Mech. 204 1
Google Scholar
[18] Sano M, Wu X Z, Libchaber A 1989 Phys. Rev. A 40 6421
Google Scholar
[19] 包芸, 何建超, 高振源 2019 68 164701
Google Scholar
Bao Y, He J C, Gao Z Y 2019 Acta Phys. Sin. 68 164701
Google Scholar
[20] Gao Z Y, Luo J H, Bao Y 2018 Chin. Phys. B 27 104702
Google Scholar
[21] Verzicco R, Camuss I R 1999 J. Fluid Mech. 383 55
Google Scholar
[22] Kerr R M 1996 J. Fluid Mech. 310 139
Google Scholar
[23] Li X M, He J D, Tian Y, Hao P, Huang S D 2021 J. Fluid Mech. 915 A60
Google Scholar
[24] Chen X, Huang S D, Xia K Q, Xi H D 2019 J. Fluid Mech. 877 R1
Google Scholar
[25] Xu A, Chen X, Xi H D 2021 Phys. Fluids 910 A33
Google Scholar
[26] Werne J, Deluca EE, Rosner R, Cattaneo F 1991 Phys. Rev. Lett. 67 3919
Google Scholar
[27] Bao Y, Luo J H, Ye M X 2017 J. Mech. 34 159
Google Scholar
[28] Sun X H 1995 Parallel Comput. 21 1241
Google Scholar
[29] Shishkina O, Stevens R J A M, Grossmann S, Lohse D 2010 New J. Phys. 12 075022
Google Scholar
[30] He J C, Fang M W, Gao Z Y, Huang S D, Bao Y 2021 Chin. Phys. B 30 094701
Google Scholar
[31] Gao Z Y, Bao Y, Huang S D 2019 72nd Annual Meeting of the APS Division of Fluid Dynamics Seattle, Washington, November 23–26, G14.00003
DownLoad:
Catalog
Metrics
- Abstract views: 3458
- PDF Downloads: 41
- Cited By: 0
