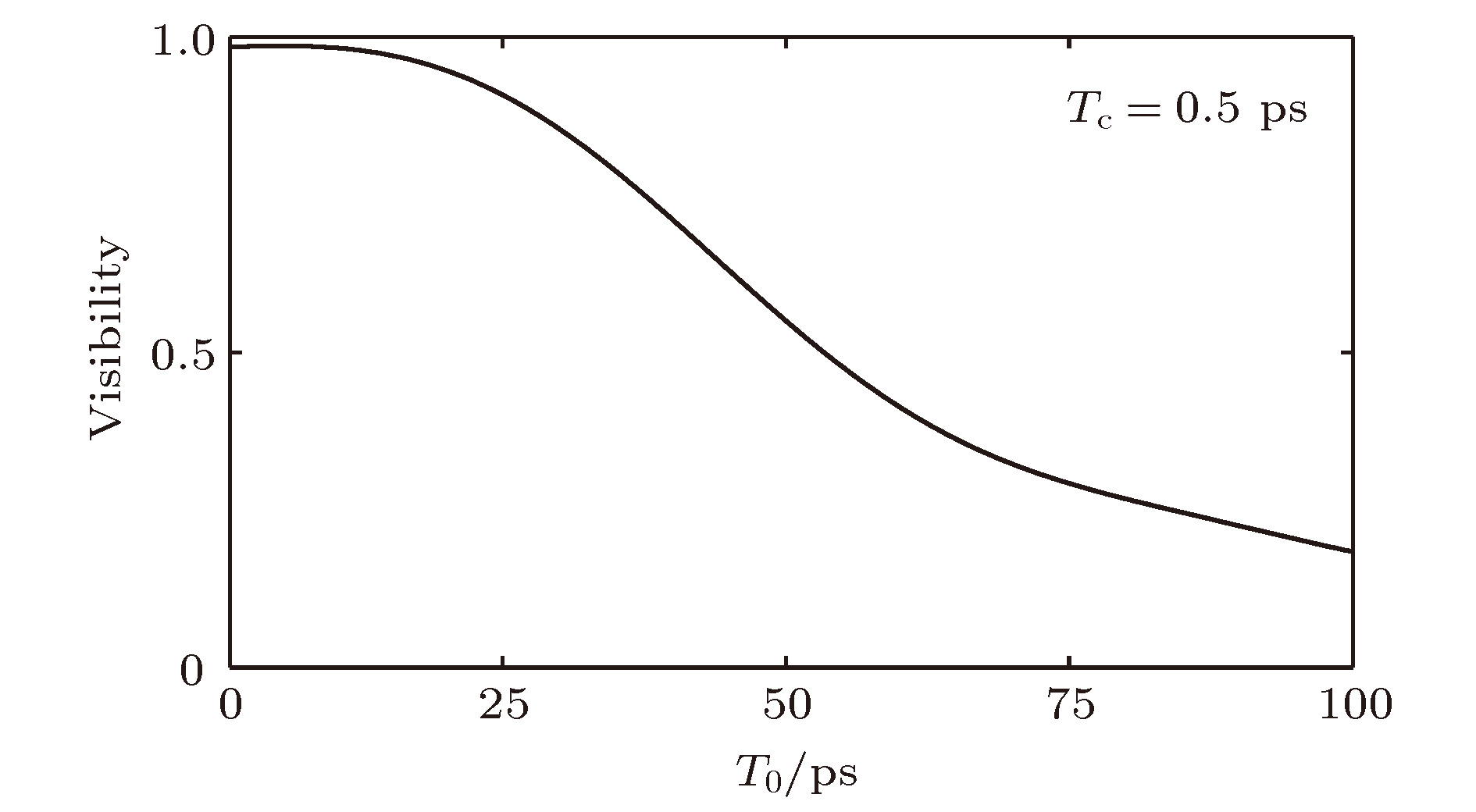
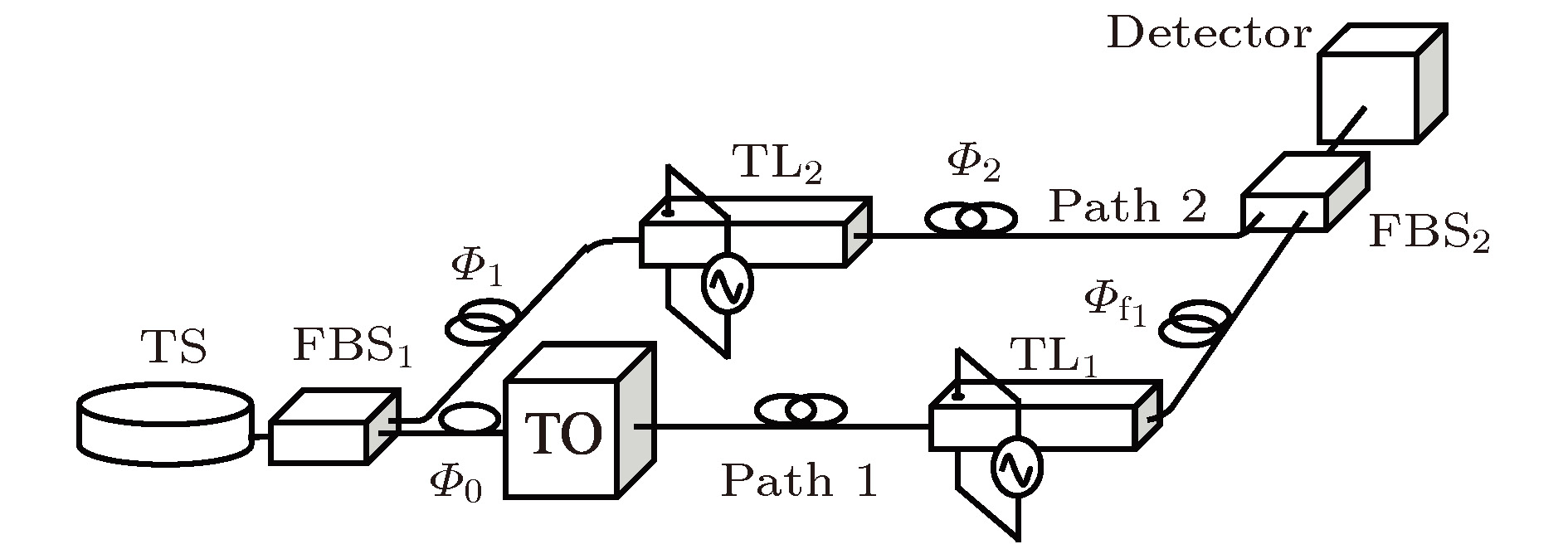
-
Different from second-order temporal ghost imaging usually realized by means of second-order correlation measurement, in this paper, we investigate theoretically temporal imaging with temporally thermal light via first-order field correlation based on a Mach-Zehnder interferometer. The paraxial wave equation describing the diffraction of light and the differential equation characterizing the dispersion of light pulse are given. Based on the similarity between these equations, the duality between the paraxial diffraction of the light in the spatial domain and the dispersion of the temporal narrow-band pulse in the dispersive medium (i.e. the space-time duality) is obtained, and the impulse response functions in the time domain for several optical systems are also presented. Then in terms of the space-time duality, we design the scheme for temporal imaging via first-order thermal field correlation based on a Mach-Zehnder interferometer and obtain the intensity expression for first-order temporal imaging according to the temporal impulse response functions, and discuss the influences of the source pulse width and coherence time on the image visibility and resolution. The result shows that the temporal signal can be reconstructed through temporal first-order temporal imaging. Furthermore, when the source’s coherence time is fixed, the image visibility decreases as the pulse width increases. However, the image resolution increases. When the source’s pulse width is fixed, the image visibility increases as the coherence time increases. And yet the image resolution decreases. Specially, when the source’s pulse width is 100 ps and the coherence time is 0.5 ps, the image quality (taking both the visibility and resolution into account) of a temporally rectangular object is satisfactory. In the simulation, the distance and width of the temporal rectangular object are 20 ps and 8 ps, respectively. It is shown that there is a dilemma between the visibility and resolution of first-order temporal imaging which is similar to the result of second-order ghost imaging. Our result discussed herein could be valuable in the reconstruction and detection of temporal signal via first-order temporal ghost imaging with temporally thermal light.
-
Keywords:
- intensity correlation /
- first-order field correlation /
- ghost imaging /
- dispersion
[1] Padgett M J, Boyd R W 2017 Phil. Trans. R. Soc. A 375 20160233
Google Scholar
[2] Pittman T B, Shih Y H, Strekalov D V, Sergienko A V 1995 Phys. Rev. A 52 R3429
Google Scholar
[3] Bennink R S, Bentley S J, Boyd R W 2002 Phys. Rev. Lett. 89 113601
Google Scholar
[4] Gatti A, Brambilla E, Bache M, Lugiato L A 2004 Phys. Rev. A 70 013802
Google Scholar
[5] Cheng J, Han S 2004 Phys. Rev. Lett. 92 093903
Google Scholar
[6] Cao D Z, Xiong J, Wang K G 2005 Phys. Rev. A 71 013801
Google Scholar
[7] Valencia A, Scarcelli G, D’ Angelo M, Shih Y H 2005 Phys. Rev. Lett. 94 063601
Google Scholar
[8] Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato L A 2005 Phys. Rev. Lett. 94 183602
Google Scholar
[9] Cai Y, Zhu S Y 2005 Phys. Rev. E 71 056607
Google Scholar
[10] Zhang D, Zhai Y H, Wu L A, Chen X H 2005 Opt. Lett. 30 2354
Google Scholar
[11] Cai Y, Wang F 2007 Opt. Lett. 32 205
Google Scholar
[12] Liu X F, Chen X H, Yao X R, Yu W K, Zhai G J, Wu L A 2014 Opt. Lett. 39 2314
Google Scholar
[13] Sun B, Edgar M P, Bowman R, Vittert L E, Welsh S, Bowman A, Padgett M J 2013 Science 340 844
Google Scholar
[14] Bromberg Y, Katz O, Silberberg Y 2009 Phys. Rev. A 79 053840
Google Scholar
[15] Shapiro J H 2008 Phys. Rev. A 78 061802
Google Scholar
[16] Zhao C Q, Gong W L, Chen M L, Li E R, Wang H, Xu W D, Han S S 2012 Appl. Phys. Lett. 101 141123
Google Scholar
[17] Hong Y, Li E R, Gong W L, Han S S 2015 Opt. Express 23 14541
Google Scholar
[18] Chen M, Li E, Gong W L, Bo Z, Xu X, Zhao C, Shen X, Xu W, Han S S 2013 Opt. Photonics J. 3 83
Google Scholar
[19] Li S, Cropp F, Kabra K, Lane T J, Wetzstein G, Musumeci P, Ratner D 2018 Phys. Rev. Lett. 121 114801
Google Scholar
[20] Cheng J 2009 Opt. Express 17 7916
Google Scholar
[21] Cheng J, Lin J 2013 Phys. Rev. A 87 043810
Google Scholar
[22] Cao D Z, Xiong J, Zhang S H, Lin L F, Gao L, Wang K G 2008 Appl. Phys. Lett. 92 201102
Google Scholar
[23] Chan K W C, O’ Sullivan M N, Boyd R W 2010 Opt. Express 18 5562
Google Scholar
[24] Zhang D J, Li H G, Zhao Q L, Wang S, Wang H B, Xiong J, Wang K G 2015 Phys. Rev. A 92 013823
Google Scholar
[25] Li H G, Zhang D J, Xu D J, Zhao Q L, Wang S, Wang H B, Xiong J, Wang K G 2015 Phys. Rev. A 92 043816
Google Scholar
[26] Katz O, Bromberg Y, Silberberg Y 2009 Appl. Phys. Lett. 95 131110
[27] 仲亚军, 刘娇, 梁文强, 赵生妹 2015 64 014202
Google Scholar
Zhong Y J, Liu J, Liang W Q, Zhao S M 2015 Acta Phys. Sin. 64 014202
Google Scholar
[28] Gao C, Wang X, Wang Z, Li Z, Du G, Chang F, Yao Z 2017 Phys. Rev. A 96 023838
Google Scholar
[29] Cao D H, Li Q H, Zhuang X C, Ren H, Zhang S H, Song X B 2018 Chin. Phys. B 27 123401
Google Scholar
[30] Yang H, Wu H, Wang H B, Cao D H, Zhang S H, Xiong J, Wang K 2018 Phys. Rev. A 98 053853
Google Scholar
[31] Salem R, Foster M A, Gaeta A L 2013 Adv. Opt. Photonics 5 274
Google Scholar
[32] Foster M A, Salem R, Geraghty D F, Turner-Foster A C, Lipson M, Gaeta A L 2008 Nature 456 81
Google Scholar
[33] Schröder J, Wang F, Clarke A, Ryckeboer E, Pelusi M , Roelens M A, Eggleton B J 2010 Opt. Commun. 283 2611
Google Scholar
[34] Fridman M, Farsi A, Okawachi Y, Gaeta A L 2012 Nature 481 62
Google Scholar
[35] Ryczkowski P, Barbier M, Friberg A T, Dudley J M, Genty G 2016 Nat. Photonics 10 167
Google Scholar
[36] Shirai T, Setälä T, Friberg A T 2010 J. Opt. Soc. Am. B 27 2549
Google Scholar
[37] Setälä T, Shirai T, Friberg A T 2010 Phys. Rev. A 82 043813
Google Scholar
[38] Chen Z, Li H, Li Y, Shi J, Zeng G 2013 Opt. Eng. 52 076103
Google Scholar
[39] Gao L, Zhang S H, Xiong J, Gan S, Feng L J, Cao D Z, Wang K G 2009 Phys. Rev. A 80 021806
Google Scholar
[40] Vabre L, Dubois A, Boccara A C 2002 Opt. Lett. 27 530
Google Scholar
[41] Kolner B H 1994 IEEE J. Quant. Electron. 30 1951
Google Scholar
[42] Cai Y, Zhu S 2004 Opt. Lett. 29 2716
Google Scholar
[43] Qu L, Bai Y, Nan S, Shen Q, Li H, Fu X 2018 Opt. Laser Technol. 104 197
Google Scholar
-
图 1 基于光场一阶关联的时域成像装置示意图
Figure 1. Schematic illustration for first-order temporal imaging.
图 2 光源相干时间为0.5 ps, 光源脉冲宽度宽度分别为5, 10, 50和100 ps条件下的关联像
Figure 2. The correlated images with different pulse widths of the source 5, 10, 50 and 100 ps, for the source’s coherence time 0.5 ps
图 3 光源相干时间Tc为0.5 ps时, 成像可见度随光源脉冲宽度的变化曲线
Figure 3. The imaging visibility as a function of the source’s pulse width for the source’s coherence time 0.5 ps
图 4 光源脉冲宽度为T0 = 100 ps, 光源相干时间Tc分别为0.5, 1.5, 5和10 ps条件下的关联像
Figure 4. The correlated images with different source’s coherence time 0.5, 1.5, 5 and 10 ps, for the source’s pulse width 100 ps
图 5 光源脉冲宽度为100 ps时, 成像可见度随光源相干时间的变化曲线
Figure 5. The imaging visibility as a function of the source coherence time for the source’s pulse width 100 ps.
-
[1] Padgett M J, Boyd R W 2017 Phil. Trans. R. Soc. A 375 20160233
Google Scholar
[2] Pittman T B, Shih Y H, Strekalov D V, Sergienko A V 1995 Phys. Rev. A 52 R3429
Google Scholar
[3] Bennink R S, Bentley S J, Boyd R W 2002 Phys. Rev. Lett. 89 113601
Google Scholar
[4] Gatti A, Brambilla E, Bache M, Lugiato L A 2004 Phys. Rev. A 70 013802
Google Scholar
[5] Cheng J, Han S 2004 Phys. Rev. Lett. 92 093903
Google Scholar
[6] Cao D Z, Xiong J, Wang K G 2005 Phys. Rev. A 71 013801
Google Scholar
[7] Valencia A, Scarcelli G, D’ Angelo M, Shih Y H 2005 Phys. Rev. Lett. 94 063601
Google Scholar
[8] Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato L A 2005 Phys. Rev. Lett. 94 183602
Google Scholar
[9] Cai Y, Zhu S Y 2005 Phys. Rev. E 71 056607
Google Scholar
[10] Zhang D, Zhai Y H, Wu L A, Chen X H 2005 Opt. Lett. 30 2354
Google Scholar
[11] Cai Y, Wang F 2007 Opt. Lett. 32 205
Google Scholar
[12] Liu X F, Chen X H, Yao X R, Yu W K, Zhai G J, Wu L A 2014 Opt. Lett. 39 2314
Google Scholar
[13] Sun B, Edgar M P, Bowman R, Vittert L E, Welsh S, Bowman A, Padgett M J 2013 Science 340 844
Google Scholar
[14] Bromberg Y, Katz O, Silberberg Y 2009 Phys. Rev. A 79 053840
Google Scholar
[15] Shapiro J H 2008 Phys. Rev. A 78 061802
Google Scholar
[16] Zhao C Q, Gong W L, Chen M L, Li E R, Wang H, Xu W D, Han S S 2012 Appl. Phys. Lett. 101 141123
Google Scholar
[17] Hong Y, Li E R, Gong W L, Han S S 2015 Opt. Express 23 14541
Google Scholar
[18] Chen M, Li E, Gong W L, Bo Z, Xu X, Zhao C, Shen X, Xu W, Han S S 2013 Opt. Photonics J. 3 83
Google Scholar
[19] Li S, Cropp F, Kabra K, Lane T J, Wetzstein G, Musumeci P, Ratner D 2018 Phys. Rev. Lett. 121 114801
Google Scholar
[20] Cheng J 2009 Opt. Express 17 7916
Google Scholar
[21] Cheng J, Lin J 2013 Phys. Rev. A 87 043810
Google Scholar
[22] Cao D Z, Xiong J, Zhang S H, Lin L F, Gao L, Wang K G 2008 Appl. Phys. Lett. 92 201102
Google Scholar
[23] Chan K W C, O’ Sullivan M N, Boyd R W 2010 Opt. Express 18 5562
Google Scholar
[24] Zhang D J, Li H G, Zhao Q L, Wang S, Wang H B, Xiong J, Wang K G 2015 Phys. Rev. A 92 013823
Google Scholar
[25] Li H G, Zhang D J, Xu D J, Zhao Q L, Wang S, Wang H B, Xiong J, Wang K G 2015 Phys. Rev. A 92 043816
Google Scholar
[26] Katz O, Bromberg Y, Silberberg Y 2009 Appl. Phys. Lett. 95 131110
[27] 仲亚军, 刘娇, 梁文强, 赵生妹 2015 64 014202
Google Scholar
Zhong Y J, Liu J, Liang W Q, Zhao S M 2015 Acta Phys. Sin. 64 014202
Google Scholar
[28] Gao C, Wang X, Wang Z, Li Z, Du G, Chang F, Yao Z 2017 Phys. Rev. A 96 023838
Google Scholar
[29] Cao D H, Li Q H, Zhuang X C, Ren H, Zhang S H, Song X B 2018 Chin. Phys. B 27 123401
Google Scholar
[30] Yang H, Wu H, Wang H B, Cao D H, Zhang S H, Xiong J, Wang K 2018 Phys. Rev. A 98 053853
Google Scholar
[31] Salem R, Foster M A, Gaeta A L 2013 Adv. Opt. Photonics 5 274
Google Scholar
[32] Foster M A, Salem R, Geraghty D F, Turner-Foster A C, Lipson M, Gaeta A L 2008 Nature 456 81
Google Scholar
[33] Schröder J, Wang F, Clarke A, Ryckeboer E, Pelusi M , Roelens M A, Eggleton B J 2010 Opt. Commun. 283 2611
Google Scholar
[34] Fridman M, Farsi A, Okawachi Y, Gaeta A L 2012 Nature 481 62
Google Scholar
[35] Ryczkowski P, Barbier M, Friberg A T, Dudley J M, Genty G 2016 Nat. Photonics 10 167
Google Scholar
[36] Shirai T, Setälä T, Friberg A T 2010 J. Opt. Soc. Am. B 27 2549
Google Scholar
[37] Setälä T, Shirai T, Friberg A T 2010 Phys. Rev. A 82 043813
Google Scholar
[38] Chen Z, Li H, Li Y, Shi J, Zeng G 2013 Opt. Eng. 52 076103
Google Scholar
[39] Gao L, Zhang S H, Xiong J, Gan S, Feng L J, Cao D Z, Wang K G 2009 Phys. Rev. A 80 021806
Google Scholar
[40] Vabre L, Dubois A, Boccara A C 2002 Opt. Lett. 27 530
Google Scholar
[41] Kolner B H 1994 IEEE J. Quant. Electron. 30 1951
Google Scholar
[42] Cai Y, Zhu S 2004 Opt. Lett. 29 2716
Google Scholar
[43] Qu L, Bai Y, Nan S, Shen Q, Li H, Fu X 2018 Opt. Laser Technol. 104 197
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6967
- PDF Downloads: 82
- Cited By: 0
