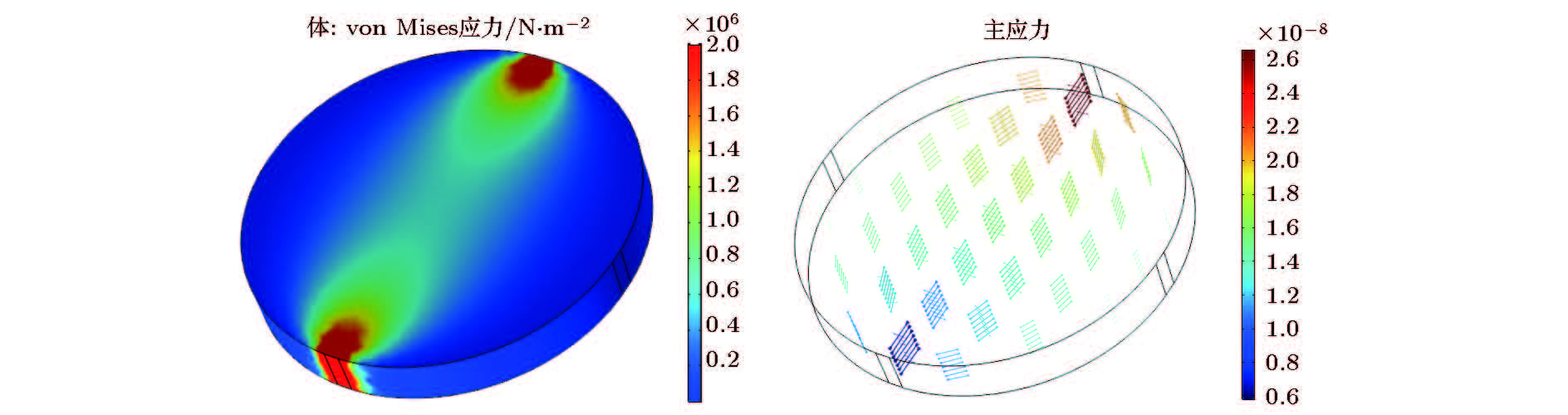
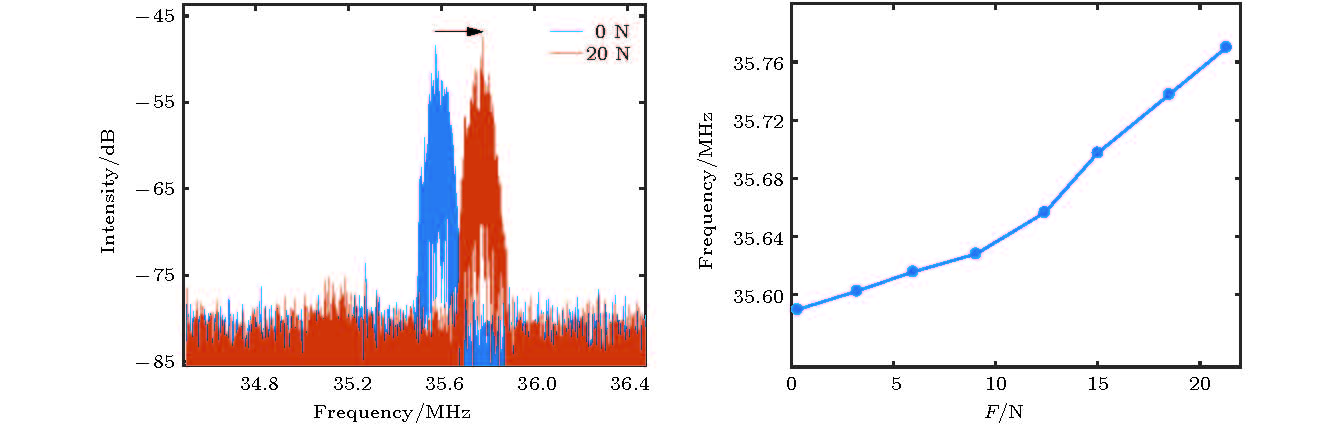
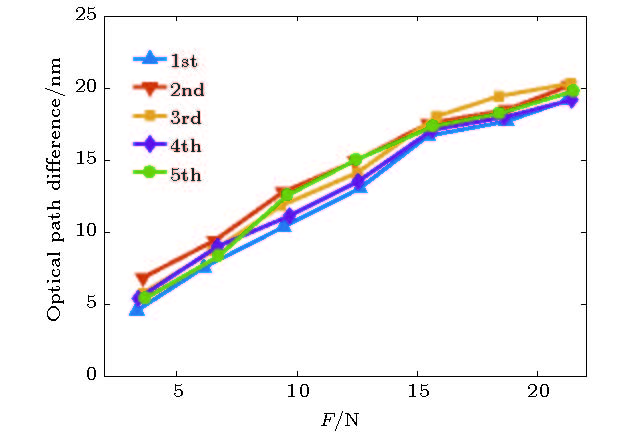
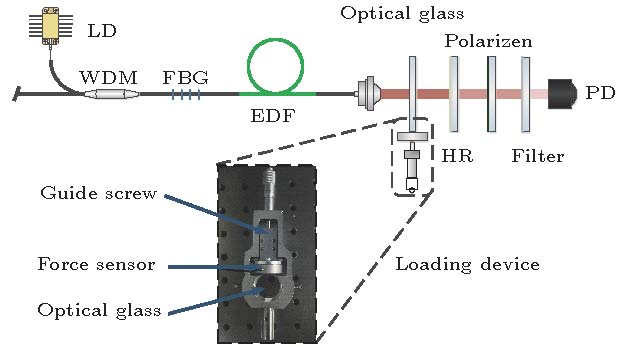
-
When the optical component works in a complicated working environment such as a large temperature difference or a multi-modal state, internal stress accumulation is likely to occur, which affects the overall performance of the optical system. The stress-optical constant of optical component in the infrared range is one of the concerns of many optical systems. In this paper, a method of measuring the internal stress-induced birefringence of optical glass based on the frequency splitting effect of 1556.16 nm erbium-doped fiber laser is proposed. The planar dielectric lenticular and fiber Bragg grating (FBG) are selected to form a linear semi-open resonator by using an erbium-doped fiber as a gain medium, and a 976 nm semiconductor laser (LD) with a single-mode pigtail output for pumping. At the pump power of 200 mW, a laser output with a spectral center wavelength of 1556.16 nm, a spectral 3-dB bandwidth of 0.018 nm, and a longitudinal mode spacing of 40.77 MHz is obtained. The birefringence and its fast axis introduced into the cavity by the fiber itself are analyzed. The force sensing structure of the optical glass to be tested is placed in the cavity, and the frequency splitting of the laser after the stress loading on the optical glass in the cavity is compared with the scenario in the empty cavity, and the bifurcation and cavity birefringence caused by the external load are obtained by combining the Jones matrix transfer equation. The load on the optical glass is gradually increased from 0 to 20 N. In the stress loading process, the direction of the stress birefringence in the optical glass is parallel to the direction of the applied force. The frequency splitting of the inner cavity increases from 35.59 MHz to 35.77 MHz, which corresponds to a 679.18 nm—682.62 nm optical path difference of the cavity. The correspondence between stress and frequency splitting is understood according to the birefringence superposition model and frequency splitting, and the result can be traced back to the basic physical quantity-wavelength. Continuous loading of the optical glass results in a system with measurement repeatability better than 0.0459 MHz. The experiment is designed to avoid the uncorrected systematic error of the system induced by the sub-cavity effect. The non-aligned error equation is obtained, and the error is calibrated. The experimental results show that the sensitivity of the instrument for K9 glass is 22060 Pa/nm and the linearity is 99.44%. The method has no damage to the surface of the optical structure, nor occlusion nor influence of its normal in-service work. It is of significance for optical lens, structural measurement and error correction, and can be widely used for accurately measuring the birefringence of optical components in the infrared band.
-
Keywords:
- fiber laser /
- frequency splitting /
- stress measurement
[1] Findlay S J, Harrison N D 2002 Mater. Today 5 18
[2] Tomozawa M, Lezzi P J, Hepburn R W J 2012 J. Non-Cryst. Solids 358 2650
[3] Guo P, Gao Q, Jia H U 2000 Opt. Pre. Eng. 1
[4] Zhu K Y, Guo B, Lu Y T, Zhang S, Tan Y D 2017 Optica 4 729
Google Scholar
[5] Jeong B H, Park J H 2018 U.S. Patent US10006982B2
[6] Norrby S J 2006 J. Cataract Refract Surg 32 545
[7] Montalto L, Paone N, Rinaldi D 2015 Opt. Eng. 54 081210−1/9
Google Scholar
[8] Vourna P, Hervoches C, Vrana M 2015 IEEE Trans. Magn. 51 1
[9] Okoro C, Levine L E, Xu R 2014 IEEE Trans. Electron. Dev. 61 2473
[10] Reul A, Lauhoff C, Krooß P 2018 Shape Memory & Superelasticity 1
[11] Yang X, Cheng Y, Zhu Z 2018 Electric Welding Machine 323
[12] Nagib N N, Bahrawi M S, Ismail L Z 2015 Opt. Laser Technol. 69 77
Google Scholar
[13] Mori A, Tomita R 2015 Instrum Sci. Technol. 43 379
Google Scholar
[14] Liu W, Liu M, Zhang S 2008 Appl. Opt. 47 5562
Google Scholar
[15] Xu Z, Luo Y, Sun Q 2019 IEEE Photonics Technol. Lett. PP 1
[16] 吕志国, 杨直, 李峰, 李强龙, 王屹山, 杨小君 2018 67 184205
Google Scholar
Lü Z G, Yang Z, Li F, Li Q L, Wang Y S, Yang X J 2018 Acta Phys. Sin. 67 184205
Google Scholar
[17] 王雪娇, 肖起榕, 闫平, 陈霄, 李丹, 杜成, 莫琦, 衣永青, 潘蓉, 巩马理 2015 64 164204
Google Scholar
Wang X J, Xiao Q R, Yan P, Chen X, Li D, Du C, Mo Q, Yi Y Q, Pan R, Gong M L 2015 Acta Phys. Sin. 64 164204
Google Scholar
[18] Wang J J, Zhang L, Zhou J, Si L, Chen J B, Feng Y C 2012 Opt. Lett. 10
[19] Hang Y S, Xiao Q R, Li D, Wang Z H, Wang X J, Yan P, Gong M L 2018 Chin. Phys. B 27 044201
-
图 1 半外腔频率分裂光纤激光器结构图
Figure 1. Structure diagram of the half external cavity frequency splitting fiber laser.
图 2 半外腔频率分裂光纤激光器光谱图
Figure 2. Optical spectrum of the half external cavity frequency splitting fiber laser.
图 3 空腔频率分裂频谱图
Figure 3. Spectrum of cavity frequency splitting.
图 4 谐振腔激光模式结构图
Figure 4. Mode structure diagram of resonant cavity.
图 5 镜片主应力大小与方向有限元仿真
Figure 5. Finite element simulation of the main stress of the lens.
图 6 (a)加载中PMB2拍频信号频谱变化; (b) PMB2拍频信号与加载力关系
Figure 6. (a)Frequency spectrum change of PMB2 in loading; (b) relationship of the PMB2 and the force.
图 7 双折射叠加图
Figure 7. Diagram of birefringence superposition.
图 8 合成相位延迟随快轴夹角变化
Figure 8. Variation of the phase delay with the fast axis angle.
图 9 玻璃应力双折射参数与加载力关系
Figure 9. Relationship of the birefringence parameters of glass stress and the force.
图 10 单次测量重复性
Figure 10. Repeatability of single measurement.
图 11 应力双折射重复性实验
Figure 11. Repeatability experiment of birefringence of glass stress.
图 12 玻璃应力-光程差拟合
Figure 12. Fitting of glass stress and optical path difference.
-
[1] Findlay S J, Harrison N D 2002 Mater. Today 5 18
[2] Tomozawa M, Lezzi P J, Hepburn R W J 2012 J. Non-Cryst. Solids 358 2650
[3] Guo P, Gao Q, Jia H U 2000 Opt. Pre. Eng. 1
[4] Zhu K Y, Guo B, Lu Y T, Zhang S, Tan Y D 2017 Optica 4 729
Google Scholar
[5] Jeong B H, Park J H 2018 U.S. Patent US10006982B2
[6] Norrby S J 2006 J. Cataract Refract Surg 32 545
[7] Montalto L, Paone N, Rinaldi D 2015 Opt. Eng. 54 081210−1/9
Google Scholar
[8] Vourna P, Hervoches C, Vrana M 2015 IEEE Trans. Magn. 51 1
[9] Okoro C, Levine L E, Xu R 2014 IEEE Trans. Electron. Dev. 61 2473
[10] Reul A, Lauhoff C, Krooß P 2018 Shape Memory & Superelasticity 1
[11] Yang X, Cheng Y, Zhu Z 2018 Electric Welding Machine 323
[12] Nagib N N, Bahrawi M S, Ismail L Z 2015 Opt. Laser Technol. 69 77
Google Scholar
[13] Mori A, Tomita R 2015 Instrum Sci. Technol. 43 379
Google Scholar
[14] Liu W, Liu M, Zhang S 2008 Appl. Opt. 47 5562
Google Scholar
[15] Xu Z, Luo Y, Sun Q 2019 IEEE Photonics Technol. Lett. PP 1
[16] 吕志国, 杨直, 李峰, 李强龙, 王屹山, 杨小君 2018 67 184205
Google Scholar
Lü Z G, Yang Z, Li F, Li Q L, Wang Y S, Yang X J 2018 Acta Phys. Sin. 67 184205
Google Scholar
[17] 王雪娇, 肖起榕, 闫平, 陈霄, 李丹, 杜成, 莫琦, 衣永青, 潘蓉, 巩马理 2015 64 164204
Google Scholar
Wang X J, Xiao Q R, Yan P, Chen X, Li D, Du C, Mo Q, Yi Y Q, Pan R, Gong M L 2015 Acta Phys. Sin. 64 164204
Google Scholar
[18] Wang J J, Zhang L, Zhou J, Si L, Chen J B, Feng Y C 2012 Opt. Lett. 10
[19] Hang Y S, Xiao Q R, Li D, Wang Z H, Wang X J, Yan P, Gong M L 2018 Chin. Phys. B 27 044201
DownLoad:
Catalog
Metrics
- Abstract views: 7411
- PDF Downloads: 71
- Cited By: 0
