-
In this paper, we present a scheme to realize an unconventional photon blockade effect in a Fabry-Perot cavity and optical parametric amplifier (OPA) composite system. The system includes a tunable phase of complex driving strength, the second-order correlation function is used to describe the photon statistical properties. The numerical simulation of the photon blockade effect is conducted with different parameters. Our calculations show that the unconventional photon blockade effect can be controlled by the tunable phase of complex driving strength. Under the weak driving condition, the exact optimal conditions for strong photon anti-bunching are analytically derived (i.e. the optimal nonlinear gain of optical parametric amplifier and the phase of the field driving for the strong photon anti-bunching are obtained), and obtain the analytic calculations of the second-order correlation function. Under the optimal conditions, we perform a numerical simulation with different parameters. The optimal conditions for strong photon anti-bunching are found by analytic calculations, which are in good agreement with the numerical results. The results provide a platform for coherently operating the photon blockade and have potential applications in quantum information processing and quantum optical devices.
[1] Imamoglu A, Schmidt H, Woods G, Deutsch M 1997 Phys. Rev. Lett. 79 1467
Google Scholar
[2] Liew T C H, Savona V 2010 Phys. Rev. Lett. 104 183601
Google Scholar
[3] Cao C, Mi S C, Wang T, Zhang R, Wang C 2016 IEEE J. Quantum Electron. 52 7000205
Google Scholar
[4] Cao C, Mi S C, Gao Y P, He L Y, Yang D, Wang T J, Zhang R, Wang C 2016 Sci. Rep. 6 22920
Google Scholar
[5] Cao Cong, Chen Xi, Duan Y W, Fan L, Zhang R, Wang T J, Wang C 2017 Optik 130 659
Google Scholar
[6] 张秀龙, 鲍倩倩, 杨明珠, 田雪松 2018 67 104203
Google Scholar
Zhang X L, Bao Q Q, Yang M Z, Tian X S 2018 Acta Phys. Sin. 67 104203
Google Scholar
[7] 廖庆洪, 叶杨, 李红珍, 周南润 2018 67 40302
Google Scholar
Liao Q H, Ye Y, Li H Z, Zhou N R 2018 Acta Phys. Sin. 67 40302
Google Scholar
[8] Birnbaum K M, Boca A, Miller R, Boozer A D, Northup T E, Kimble H J 2005 Nature 436 87
Google Scholar
[9] Greentree A D, Tahan C, Cole J H, Hollenberg L C L 2006 Nat. Phys. 2 856
Google Scholar
[10] Angelakis D G, Santos M F, Bose S 2007 Phys. Rev. A 76 031805
Google Scholar
[11] Shen H Z, Zhou Y H, Yi X X 2015 Phys. Rev. A 91 063808
Google Scholar
[12] Shen H Z, Zhou Y H, Yi X X 2014 Phys. Rev. A 90 023849
Google Scholar
[13] Irvine W T M, Hennessy K, Bouwmeester D 2006 Phys. Rev. Lett. 96 057405
Google Scholar
[14] Zhou Y H, Shen H Z, Yi X X 2015 Phys. Rev. A 92 023838
Google Scholar
[15] Shen H Z, Zhou Y H, Liu H D, Wang G C, Yi X X 2015 Opt. Express 23 32835
Google Scholar
[16] Zhou Y H, Zhang S S, Shen H Z, Yi X X 2017 Opt. Lett. 42 1289
Google Scholar
[17] Shen H Z, Shang C, Zhou Y H, Yi X X 2018 Phys. Rev. A 98 023856
Google Scholar
[18] Shen H Z, Xu S, Zhou Y H, Wang G C, Yi X X 2018 J. Phys. B 51 035503
Google Scholar
[19] Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819
Google Scholar
[20] Su S L, Tian Y Z, Shen H Z, Zang H P, Liang E J, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[21] Su S L, Gao Y, Liang E J, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[22] Su S L, Liang E J, Zhang S, Wen J J, Sun L L, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[23] Zhou Y H, Shen H Z, Shao X Q, Yi X X 2016 Opt. Express 24 17332
Google Scholar
[24] Tang J, Geng W, Xu X 2015 Sci. Rep. 5 9252
Google Scholar
[25] Majumdar A, Bajcsy M, Rundquist A, Vuckovic J 2012 Phys. Rev. Lett. 108 183601
Google Scholar
[26] Zhang W, Yu Z, Liu Y, Peng Y 2014 Phys. Rev. A 8 043832
[27] Flayac H, Savona V 2016 Phys. Rev. A 94 013815
Google Scholar
[28] Gerace D, Savona V 2014 Phys. Rev. A 89 031803
Google Scholar
[29] Lemonde M A, Didier N, Clerk A A 2014 Phys. Rev. A 90 063824
Google Scholar
[30] Xu X W, Li Y J 2013 J. Phys. B 46 035502
Google Scholar
[31] Wicz A, Li H R, Miranoao J Q, Nori F, Jing H 2018 Phys. Rev. Lett. 121 153601
Google Scholar
[32] 石海泉, 谢智强, 徐勋卫, 刘念华 2018 67 044203
Google Scholar
Shi H Q, Xie Z Q, Xu X W, Liu N H 2018 Acta Phys. Sin. 67 044203
Google Scholar
[33] Sarma B, Sarma A K 2017 Phys. Rev. A 96 053827
Google Scholar
-
图 1 (a) 用激光抽运OPA, 在腔内产生参量放大的腔结构示意图; (b) 量子干涉系统的跃迁路径
Figure 1. (a) Schematic diagram of the cavity setup with an OPA which is pumped by a laser to produce parametric amplification in the cavity; (b) transition paths of the system for quantum interference.
图 3 等时二阶关联函数
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ 数值结果随OPA非线性增益G和相位$\theta $ 的等高线图${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$\phi = 0.5\;{\rm{rad}}$ Figure 3. Contour plot of the second-order correlation functions
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ vs. the nonlinear gain G of the OPA and phase$\theta $ . Other parameters are${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$\phi = 0.5\;{\rm{rad}}$ .
图 2 等时二阶关联函数
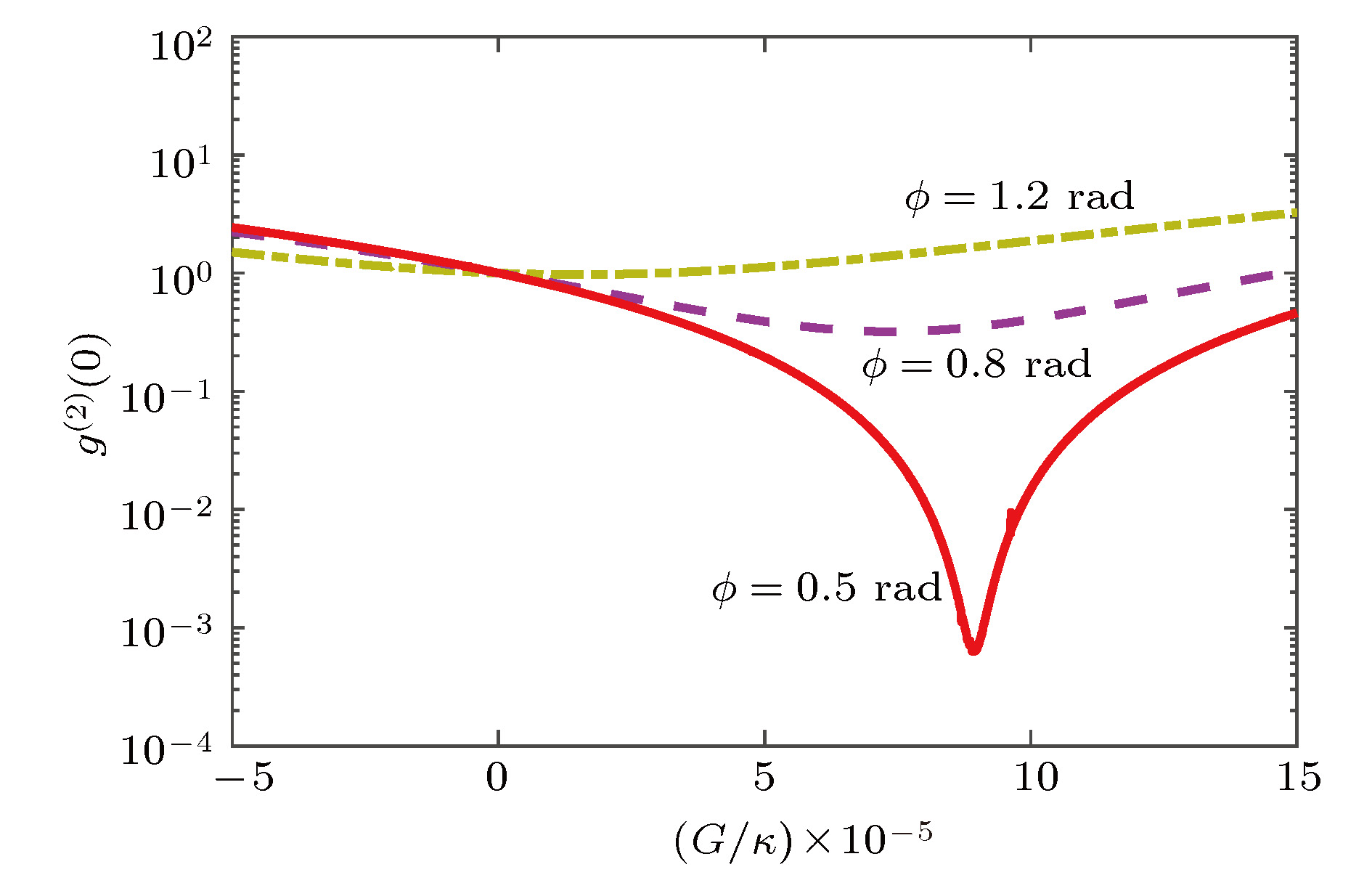
${g^{\left(2\right)}}(0)$ 随OPA非线性增益G的变化${\varOmega / {\kappa = 0.01}}$ ,$\theta = - 0.0341{\text{π}}$ ,${\varDelta _a} = 1$ Figure 2. Variation curves of the zero-time-delay second-order correlation function
${g^{\left(2\right)}}(0)$ with the nonlinear gain G of the OPA. Other parameters are${\varOmega / {\kappa = 0.01}}$ ,$\theta = - 0.0341{\text{π}}$ ,${\varDelta _a} = 1$ .
图 4 等时二阶关联函数
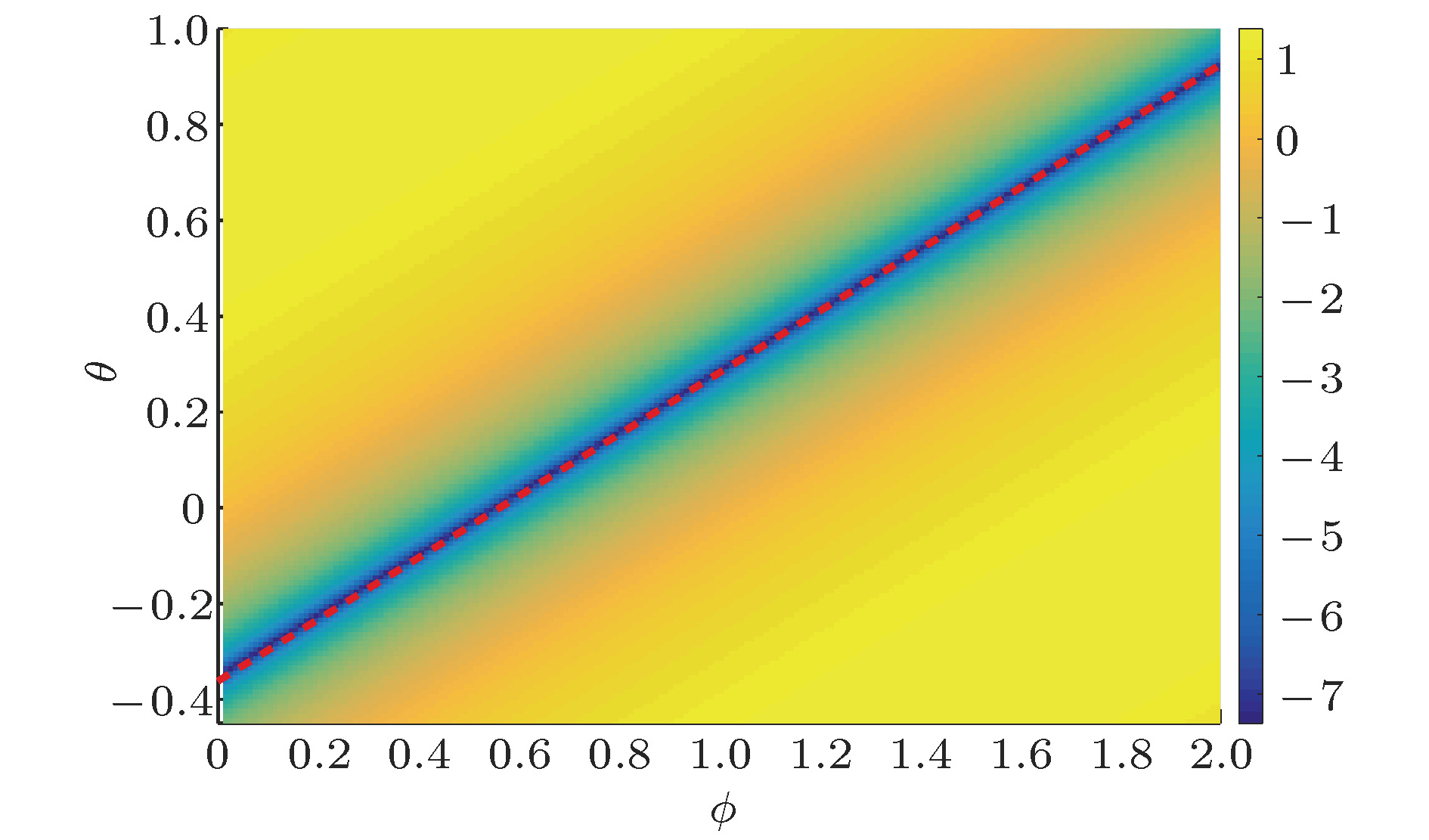
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ 数值结果随相位$\theta $ 和$\phi $ 的等高线图${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$G = {G_{\rm opt}}$ Figure 4. Contour plot of the second-order correlation functions
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ vs. the phase$\theta $ and$\phi $ . Other parameters are${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$G = {G_{\rm opt}}$ .
图 5 等时二阶关联函数
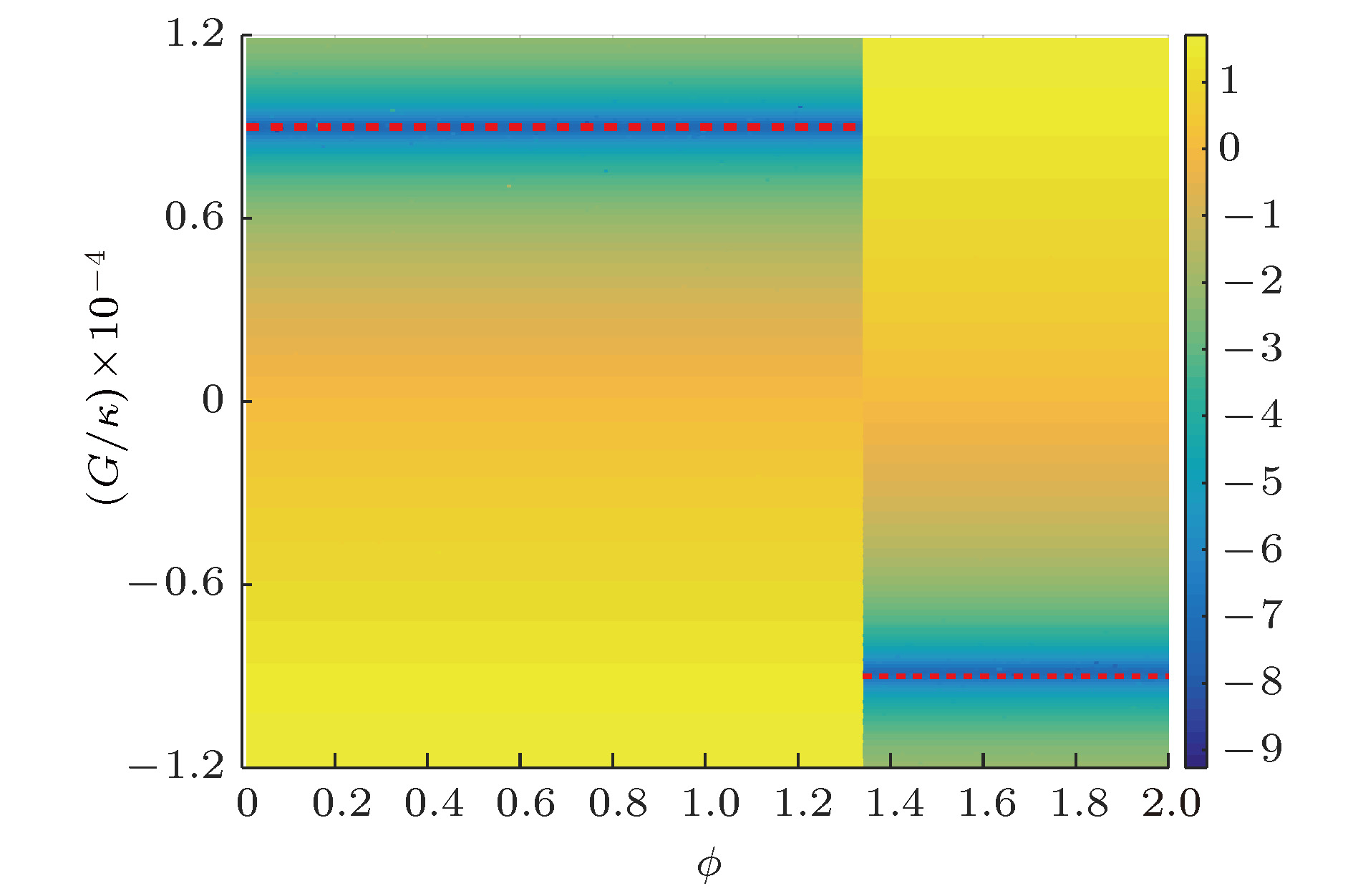
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ 数值结果随OPA非线性增益$G$ 和相位$\phi $ 变化的等高线图${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$G = {G_{\rm opt}}$ Figure 5. Contour plot of the second-order correlation functions
$\lg \left[ {{g^{\left(2\right)}}\left(0\right)} \right]$ vs. the nonlinear gain of the optical parametric amplifier$G$ and phase$\phi $ . Other parameters are${\varOmega / {\kappa = 0.01}}$ ,${\varDelta _a} = 1$ ,$G = {G_{\rm opt}}$ .
图 6 (a) 二阶关联函数
${g^{\left(2\right)}}(0)$ 随OPA非线性增益$G$ 的变化, 其中蓝色实线由数值求解方程(3)得出, 红色菱形由(13)和(15)式解析得出; 其他参数为${\varDelta _a} = 1, \; \varOmega /\kappa = 0.01,$ $\phi = 0.5\;{\rm{rad}}, \; \theta = {\theta _{\rm opt}}$ ; (b) 二阶关联函数${g^{\left(2\right)}}(0)$ 随相位$\theta $ 的变化, 蓝色实线由数值求解方程(3)得出, 红色圆形由(13)和(15)式解析得出; 其他参数为${\varDelta _a} = 1, \;\varOmega /\kappa = 0.01,$ $\phi = 0.5\;{\rm{rad}}, \;G = {G_{\rm opt}}$ Figure 6. (a) The second-order correlation functions
${g^{\left(2\right)}}(0)$ vs. the nonlinear gain of the optical parametric amplifier$G$ ; the blue solid line indicates the numerical results by numerically solving Eq. (3) and the red diamond corresponds to the analytical results of Eq. (13) and Eq. (15); other parameters are${\varDelta _a} = 1, \; \varOmega /\kappa = 0.01, \; \phi = 0.5\;{\rm{rad}}, \; \theta = {\theta _{\rm opt}}$ ; (b) the second-order correlation functions${g^{\left(2\right)}}(0)$ vs. the phase$\theta $ ; the blue solid line indicates the numerical results by numerically solving Eq. (3) and the red diamond corresponds to the analytical results of Eq. (13) and Eq. (15). Other parameters are${\varDelta _a} = 1, \;\varOmega /\kappa = 0.01, \;\phi = 0.5\;{\rm{rad}},$ G = Gopt. -
[1] Imamoglu A, Schmidt H, Woods G, Deutsch M 1997 Phys. Rev. Lett. 79 1467
Google Scholar
[2] Liew T C H, Savona V 2010 Phys. Rev. Lett. 104 183601
Google Scholar
[3] Cao C, Mi S C, Wang T, Zhang R, Wang C 2016 IEEE J. Quantum Electron. 52 7000205
Google Scholar
[4] Cao C, Mi S C, Gao Y P, He L Y, Yang D, Wang T J, Zhang R, Wang C 2016 Sci. Rep. 6 22920
Google Scholar
[5] Cao Cong, Chen Xi, Duan Y W, Fan L, Zhang R, Wang T J, Wang C 2017 Optik 130 659
Google Scholar
[6] 张秀龙, 鲍倩倩, 杨明珠, 田雪松 2018 67 104203
Google Scholar
Zhang X L, Bao Q Q, Yang M Z, Tian X S 2018 Acta Phys. Sin. 67 104203
Google Scholar
[7] 廖庆洪, 叶杨, 李红珍, 周南润 2018 67 40302
Google Scholar
Liao Q H, Ye Y, Li H Z, Zhou N R 2018 Acta Phys. Sin. 67 40302
Google Scholar
[8] Birnbaum K M, Boca A, Miller R, Boozer A D, Northup T E, Kimble H J 2005 Nature 436 87
Google Scholar
[9] Greentree A D, Tahan C, Cole J H, Hollenberg L C L 2006 Nat. Phys. 2 856
Google Scholar
[10] Angelakis D G, Santos M F, Bose S 2007 Phys. Rev. A 76 031805
Google Scholar
[11] Shen H Z, Zhou Y H, Yi X X 2015 Phys. Rev. A 91 063808
Google Scholar
[12] Shen H Z, Zhou Y H, Yi X X 2014 Phys. Rev. A 90 023849
Google Scholar
[13] Irvine W T M, Hennessy K, Bouwmeester D 2006 Phys. Rev. Lett. 96 057405
Google Scholar
[14] Zhou Y H, Shen H Z, Yi X X 2015 Phys. Rev. A 92 023838
Google Scholar
[15] Shen H Z, Zhou Y H, Liu H D, Wang G C, Yi X X 2015 Opt. Express 23 32835
Google Scholar
[16] Zhou Y H, Zhang S S, Shen H Z, Yi X X 2017 Opt. Lett. 42 1289
Google Scholar
[17] Shen H Z, Shang C, Zhou Y H, Yi X X 2018 Phys. Rev. A 98 023856
Google Scholar
[18] Shen H Z, Xu S, Zhou Y H, Wang G C, Yi X X 2018 J. Phys. B 51 035503
Google Scholar
[19] Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819
Google Scholar
[20] Su S L, Tian Y Z, Shen H Z, Zang H P, Liang E J, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[21] Su S L, Gao Y, Liang E J, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[22] Su S L, Liang E J, Zhang S, Wen J J, Sun L L, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[23] Zhou Y H, Shen H Z, Shao X Q, Yi X X 2016 Opt. Express 24 17332
Google Scholar
[24] Tang J, Geng W, Xu X 2015 Sci. Rep. 5 9252
Google Scholar
[25] Majumdar A, Bajcsy M, Rundquist A, Vuckovic J 2012 Phys. Rev. Lett. 108 183601
Google Scholar
[26] Zhang W, Yu Z, Liu Y, Peng Y 2014 Phys. Rev. A 8 043832
[27] Flayac H, Savona V 2016 Phys. Rev. A 94 013815
Google Scholar
[28] Gerace D, Savona V 2014 Phys. Rev. A 89 031803
Google Scholar
[29] Lemonde M A, Didier N, Clerk A A 2014 Phys. Rev. A 90 063824
Google Scholar
[30] Xu X W, Li Y J 2013 J. Phys. B 46 035502
Google Scholar
[31] Wicz A, Li H R, Miranoao J Q, Nori F, Jing H 2018 Phys. Rev. Lett. 121 153601
Google Scholar
[32] 石海泉, 谢智强, 徐勋卫, 刘念华 2018 67 044203
Google Scholar
Shi H Q, Xie Z Q, Xu X W, Liu N H 2018 Acta Phys. Sin. 67 044203
Google Scholar
[33] Sarma B, Sarma A K 2017 Phys. Rev. A 96 053827
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7259
- PDF Downloads: 84
- Cited By: 0
