-
The Buck-Sukumar (BS) model, with a nonlinear coupling between the atom and the light field, is well defined only when its coupling strength is lower than a critical coupling. Its energy collapses at a critical coupling and is unbounded beyond that value. In other words, the BS model is incomplete. We introduce a simple and complete BS model by adding a nonlinear photon term into the initial BS model. Considering the rotating wave approximation, this complete BS model conserves the excited number and the parity. By expanding it in the subspace of the product state between the atom and the field, we solve the time-independent Schrödinger equation to obtain the eigenenergy and eigenstate. Furthermore, we explore the influence of the nonlinear photon term on the energy spectrum and the photon blockade effect for the complete BS model by calculating the excited number and second-order correlation function. Our study shows that, the nonlinear photon term not only eliminates the energy spectral collapse but also makes it well-defined and complete in all the coupling regime. When at the resonance between the atomic and the field frequency, the nonlinear photon term breaks the harmonicity of the energy spectrum and produces a ladder of the excited number in the ground state. Because the larger nonlinear photon term inhibits the photon transition from an energy level to the higher one, it produces the single-photon projection state in the larger coupling region. Accordingly, we find that the nonlinear photon term promotes photon blockade by calculating the second-order correlation function. When at the non-resonant region, the nonlinear photon term enlarges the originally anharmonic energy ladder. For a complete BS model with the fixed nonlinear photon coupling strength and the fixed detuning, the energy level for the positive detuning is lower than that with the negative detuning, and more energy is required to overcome the absorption of a photon. Therefore, the positive detuning promotes the photon blockade. For the negative detuning, the system is more likely to absorb a photon and jump to a higher energy level, and therefore, suppresses the photon blockade. [1] Jaynes E T, Cummings F W 1963 Proc. IEEE 51 89
Google Scholar
[2] Thompson R J, Rempe G, Kimble H J 1992 Phys. Rev. Lett. 68 1132
Google Scholar
[3] Brune M, Schmidt-Kaler F, Maali A, Dreyer J, Hagley E, Raimond J M, Haroche S 1996 Phys. Rev. Lett. 76 1800
Google Scholar
[4] Leibfried D, Blatt R, Monroe C, Wineland D 2003 Rev. Mod. Phys. 75 281
Google Scholar
[5] Englund D, Faraon A, Fushman I, Stoltz N, Petroff P, Vučković J 2007 Nat. Lett. 450 857
Google Scholar
[6] Frisk-Kokum A, Miranowicz A, De Liberato S, Savasta S, Nori F 2019 Nat. Rev. Phys. 1 19
Google Scholar
[7] Rossatto D Z, Villas-Bǒas C J, Sanz M, Solano E 2017 Phys. Rev. A 96 013849
Google Scholar
[8] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[9] Chen Q, Wang C, He S, Wang K 2012 Phys. Rev. A 86 023822
Google Scholar
[10] Buck B, Sukumar C V 1981 Phys. Lett. A 81 132
[11] Ng K M, Lo C F, Liu K L 2000 Phys. A: Stat. Mech. Appl. 275 463
Google Scholar
[12] Rodríguez-Lara B M, Soto-Eguibar F, Cárdenas A Z, Moya-Cessa H M 2013 Opt. Express 21 12888
Google Scholar
[13] Rodríguez-Lara B M 2014 J. Opt. Soc. Am. B 31 1719
Google Scholar
[14] Penna V, Raffa F A 2014 Int. J. Quantum Inf. 12 1560010
Google Scholar
[15] Cordeiro F, Providência C, da Providência J, Nishiyama S 2007 J. Phys. A: Math. Theor. 40 12153
Google Scholar
[16] Liu X Y, Ren X Z, Wang C, Gao X L, Wang K L 2020 Commun. Theor. Phys. 72 065502
Google Scholar
[17] Felicetti S, Rossatto D Z, Rico E, Solano E, Forn-Díaz P 2018 Phys. Rev. A. 97 013851
Google Scholar
[18] Duan L, Xie Y F, Braak D, Chen Q H 2016 J. Phys. A: Math. Theor. 49 464002
Google Scholar
[19] Lo C F 2020 Sci. Rep. 10 18761
Google Scholar
[20] Cui S, Grémaud B, Guo W, Batrouni G G 2020 Phys. Rev. A 102 033334
Google Scholar
[21] Moya-Cessa H, Soto-Eguibar F, Vargas-Martínez J M, Juárez- Amaro R, Zúñiga-Segundo A 2012 Phys. Rep. 513 229
Google Scholar
[22] Valverde C, Gonçalves V G, Baseia B 2016 Phys. A: Stat. Mech. Appl. 446 171
Google Scholar
[23] Pritchard J D 2012 Ph. D. Dissertation (Durham: Durham University)
[24] Grünwald P 2019 New J. Phys. 21 093003
Google Scholar
[25] Li M C, Chen A X 2019 Atom. Appl. Sci. 9 980
Google Scholar
[26] Birnbaum K M, Boca A, Miller R, Boozer A D, Northup T E, Kimble H J 2005 Nature 436 87
Google Scholar
[27] Michler P, Kiraz A, Becher C, Schoenfeld W V, Petroff P M, Zhang L, Hu E, Imamoǧlu A 2005 Science 290 2282
Google Scholar
[28] Greentree A D, Tahan C, Cole J H, Hollenberg L C 2006 Nat. Phys. 2 856
Google Scholar
[29] Koch J, Hur K L 2009 Phys. Rev. A. 80 023811
Google Scholar
-
图 1 共振时
$\varDelta=0$ , 非线性光子耦合项对旋波近似下的 BS 模型能谱的影响, 其中 (a)$ U=0 $ , (b)$ U=0.1 $ , 红色代表偶宇称态, 蓝色代表奇宇称态, 实线代表$ E_{n}^{\left(+\right)} $ 支, 虚线代表$ E_{n}^{\left(-\right)} $ 支Figure 1. Influence of the nonlinear photon term on the BS model with the rotating wave approximation at resonance
$\varDelta=0$ , where (a)$ U=0 $ , (b)$ U=0.1 $ , the red (blue) line represents the energy level with even (odd) parity while the solid (dashed) line represents the energy level of$ E_{n}^{\left(+\right)} $ ($ E_{n}^{\left(-\right)} $ ).
图 2 共振时
$ \varDelta=0 $ , 非线性光子项对旋波近似下BS模型激发数$ \langle\hat{N}_{{\rm{e}}}\rangle $ 的影响Figure 2. For the BS model with the rotating wave approximation at resonance
$ \varDelta=0 $ , the influence of the nonlinear photon term on the excited number$ \langle\hat{N}_{{\rm{e}}}\rangle $ 
图 3 共振时
$ \varDelta=0 $ , 非线性光子项对旋波近似下的BS模型能级差$ \text{δ} E_{m}, \; m=d, \; 0, \; 1, \; \cdots $ 的影响 (a)$ U=0 $ ; (b)$ U \ne 0 $ , 图中红色线表示$ U=1 $ , 黑色线表示$ U=0.5 $ Figure 3. For the BS model with the rotating wave approximation at resonance
$ \varDelta=0 $ , the influence of the nonlinear photon term on the nearest neighbor energy level difference$\text{δ} E_{m}, \; m=d, \; 0,\; 1, \; \cdots $ , where (a)$ U=0 $ , (b)$ U \ne 0 $ and the red (black) line represents$ U=1(0.5) $ in panel (b)
图 4 共振时
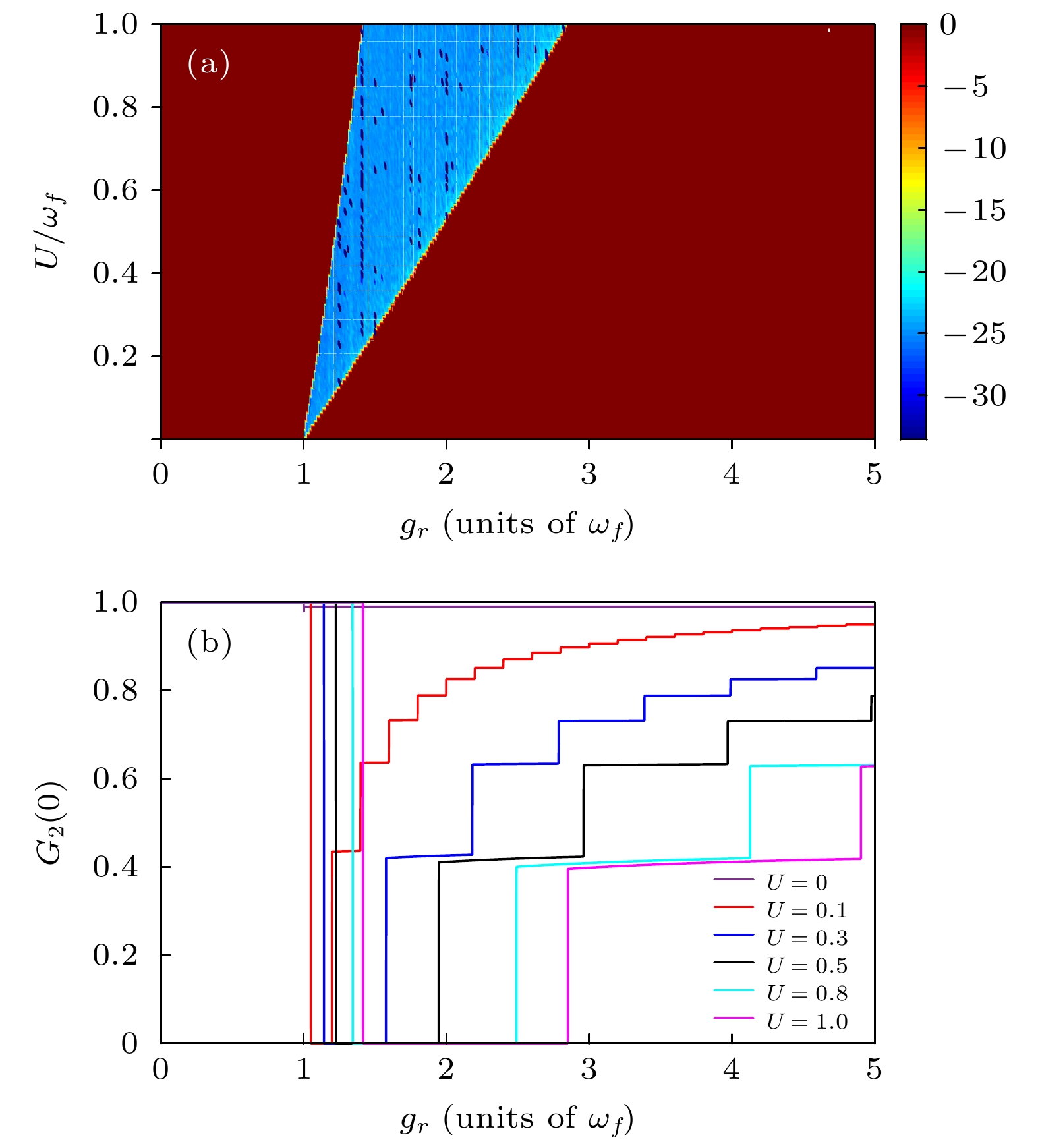
$ \varDelta=0 $ , 非线性光子项对旋波近似下 BS 模型的基态二阶关联函数$ G_{2}\left(0\right) $ 的影响 (a)$ G_{2}\left(0\right) $ 随非线性光子 U和耦合强度$ g_{{\rm{r}}} $ 的变化, 颜色代表对$ G_{2}\left(0\right) $ 取对数后$ \log\left(G_{2}\left(0\right)\right) $ 的值; (b) 不同非线性光子耦合强度U下$ G_{2}\left(0\right) $ 随耦合强度$ g_{{\rm{r}}} $ 的变化Figure 4. For the BS model with the rotating wave approximation at resonance
$ \varDelta=0 $ , the influence of the nonlinear photon term on the second-order correlation function$ G_{2}\left(0\right) $ : (a) Variation of$ G_{2}\left(0\right) $ as a function of the nonlinear photon term U and the coupling strength$ g_{{\rm{r}}} $ , where the color represents the value of$ \log\left(G_{2}\left(0\right)\right) $ ; (b) variation of$ G_{2}\left(0\right) $ as a function of the coupling strength$ g_{{\rm{r}}} $ for different nonlinear photon terms U
图 5 非线性光子项为
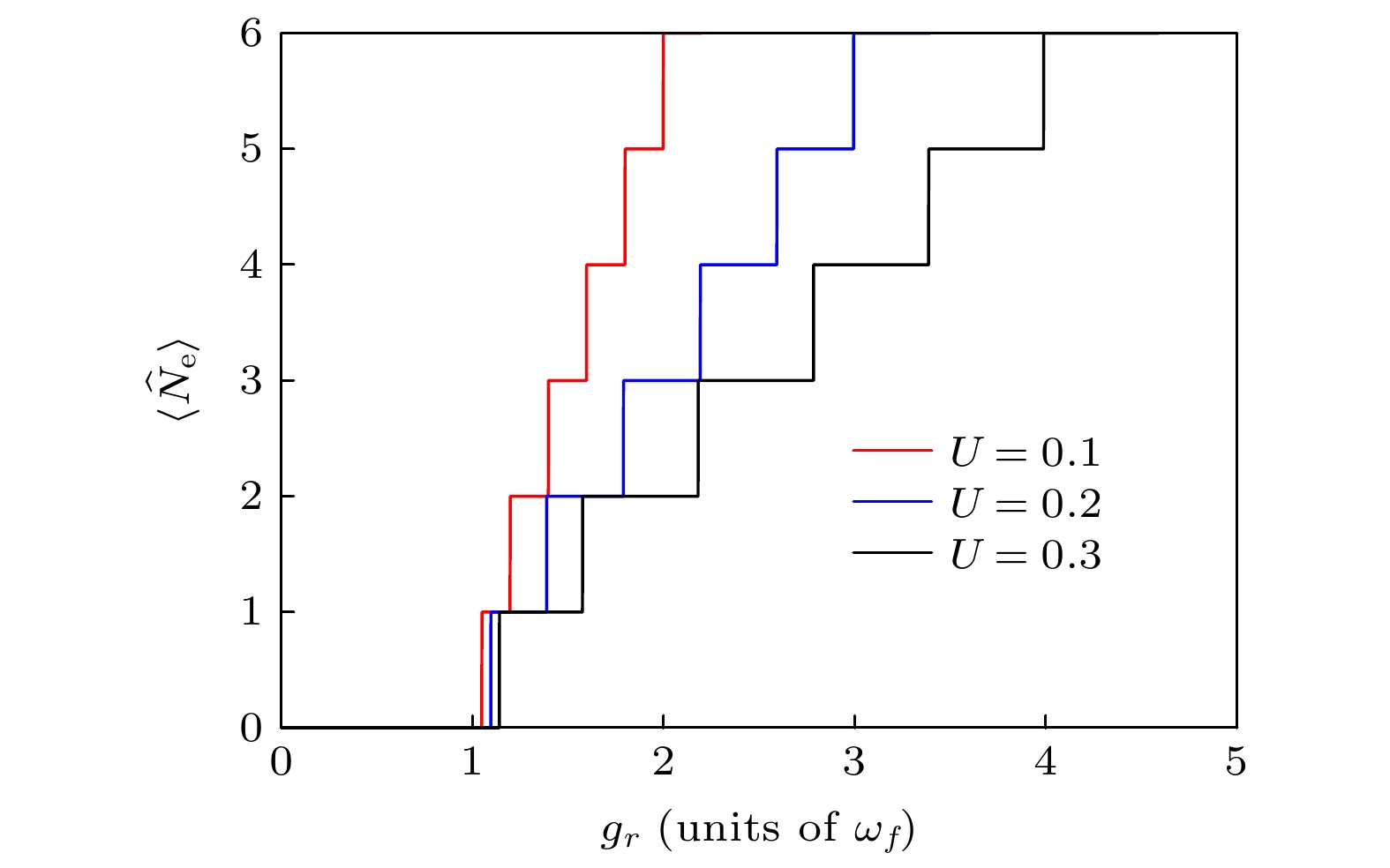
$ U=0.1 $ 时, 失谐量$ \varDelta \ne 0 $ 对旋波近似下BS模型的(a) 基态激发数$ \hat{N}_{{\rm{e}}} $ , (b) 能级差$\text{δ} E_{m}, $ $ \; m=d, \;0,\; 1$ , (c) 基态二阶关联函数$ G_{2}\left(0\right) $ 的影响. 图(b)中红色线代表$ \varDelta=-2 $ , 黑色线代表$ \varDelta=0 $ , 蓝色线代表$ \varDelta=2 $ Figure 5. For the BS model with the rotating wave approximation with the nonlinear photon term
$ U=0.1 $ , influence of the detuning$ \varDelta\ne0 $ on the (a) excited number$ \hat{N}_{{\rm{e}}} $ in the ground state, (b) nearest neighbor energy level difference$ \text{δ} E_{m},\; m=d, \;0, \;1 $ , and (c) second-order correlation function$ G_{2}\left(0\right) $ in the ground state. The red, black and blue line represent$ \varDelta=-2 $ ,$ \varDelta=0 $ and$ \varDelta=2 $ respectively in panel (b) -
[1] Jaynes E T, Cummings F W 1963 Proc. IEEE 51 89
Google Scholar
[2] Thompson R J, Rempe G, Kimble H J 1992 Phys. Rev. Lett. 68 1132
Google Scholar
[3] Brune M, Schmidt-Kaler F, Maali A, Dreyer J, Hagley E, Raimond J M, Haroche S 1996 Phys. Rev. Lett. 76 1800
Google Scholar
[4] Leibfried D, Blatt R, Monroe C, Wineland D 2003 Rev. Mod. Phys. 75 281
Google Scholar
[5] Englund D, Faraon A, Fushman I, Stoltz N, Petroff P, Vučković J 2007 Nat. Lett. 450 857
Google Scholar
[6] Frisk-Kokum A, Miranowicz A, De Liberato S, Savasta S, Nori F 2019 Nat. Rev. Phys. 1 19
Google Scholar
[7] Rossatto D Z, Villas-Bǒas C J, Sanz M, Solano E 2017 Phys. Rev. A 96 013849
Google Scholar
[8] Braak D 2011 Phys. Rev. Lett. 107 100401
Google Scholar
[9] Chen Q, Wang C, He S, Wang K 2012 Phys. Rev. A 86 023822
Google Scholar
[10] Buck B, Sukumar C V 1981 Phys. Lett. A 81 132
[11] Ng K M, Lo C F, Liu K L 2000 Phys. A: Stat. Mech. Appl. 275 463
Google Scholar
[12] Rodríguez-Lara B M, Soto-Eguibar F, Cárdenas A Z, Moya-Cessa H M 2013 Opt. Express 21 12888
Google Scholar
[13] Rodríguez-Lara B M 2014 J. Opt. Soc. Am. B 31 1719
Google Scholar
[14] Penna V, Raffa F A 2014 Int. J. Quantum Inf. 12 1560010
Google Scholar
[15] Cordeiro F, Providência C, da Providência J, Nishiyama S 2007 J. Phys. A: Math. Theor. 40 12153
Google Scholar
[16] Liu X Y, Ren X Z, Wang C, Gao X L, Wang K L 2020 Commun. Theor. Phys. 72 065502
Google Scholar
[17] Felicetti S, Rossatto D Z, Rico E, Solano E, Forn-Díaz P 2018 Phys. Rev. A. 97 013851
Google Scholar
[18] Duan L, Xie Y F, Braak D, Chen Q H 2016 J. Phys. A: Math. Theor. 49 464002
Google Scholar
[19] Lo C F 2020 Sci. Rep. 10 18761
Google Scholar
[20] Cui S, Grémaud B, Guo W, Batrouni G G 2020 Phys. Rev. A 102 033334
Google Scholar
[21] Moya-Cessa H, Soto-Eguibar F, Vargas-Martínez J M, Juárez- Amaro R, Zúñiga-Segundo A 2012 Phys. Rep. 513 229
Google Scholar
[22] Valverde C, Gonçalves V G, Baseia B 2016 Phys. A: Stat. Mech. Appl. 446 171
Google Scholar
[23] Pritchard J D 2012 Ph. D. Dissertation (Durham: Durham University)
[24] Grünwald P 2019 New J. Phys. 21 093003
Google Scholar
[25] Li M C, Chen A X 2019 Atom. Appl. Sci. 9 980
Google Scholar
[26] Birnbaum K M, Boca A, Miller R, Boozer A D, Northup T E, Kimble H J 2005 Nature 436 87
Google Scholar
[27] Michler P, Kiraz A, Becher C, Schoenfeld W V, Petroff P M, Zhang L, Hu E, Imamoǧlu A 2005 Science 290 2282
Google Scholar
[28] Greentree A D, Tahan C, Cole J H, Hollenberg L C 2006 Nat. Phys. 2 856
Google Scholar
[29] Koch J, Hur K L 2009 Phys. Rev. A. 80 023811
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3819
- PDF Downloads: 77
- Cited By: 0
