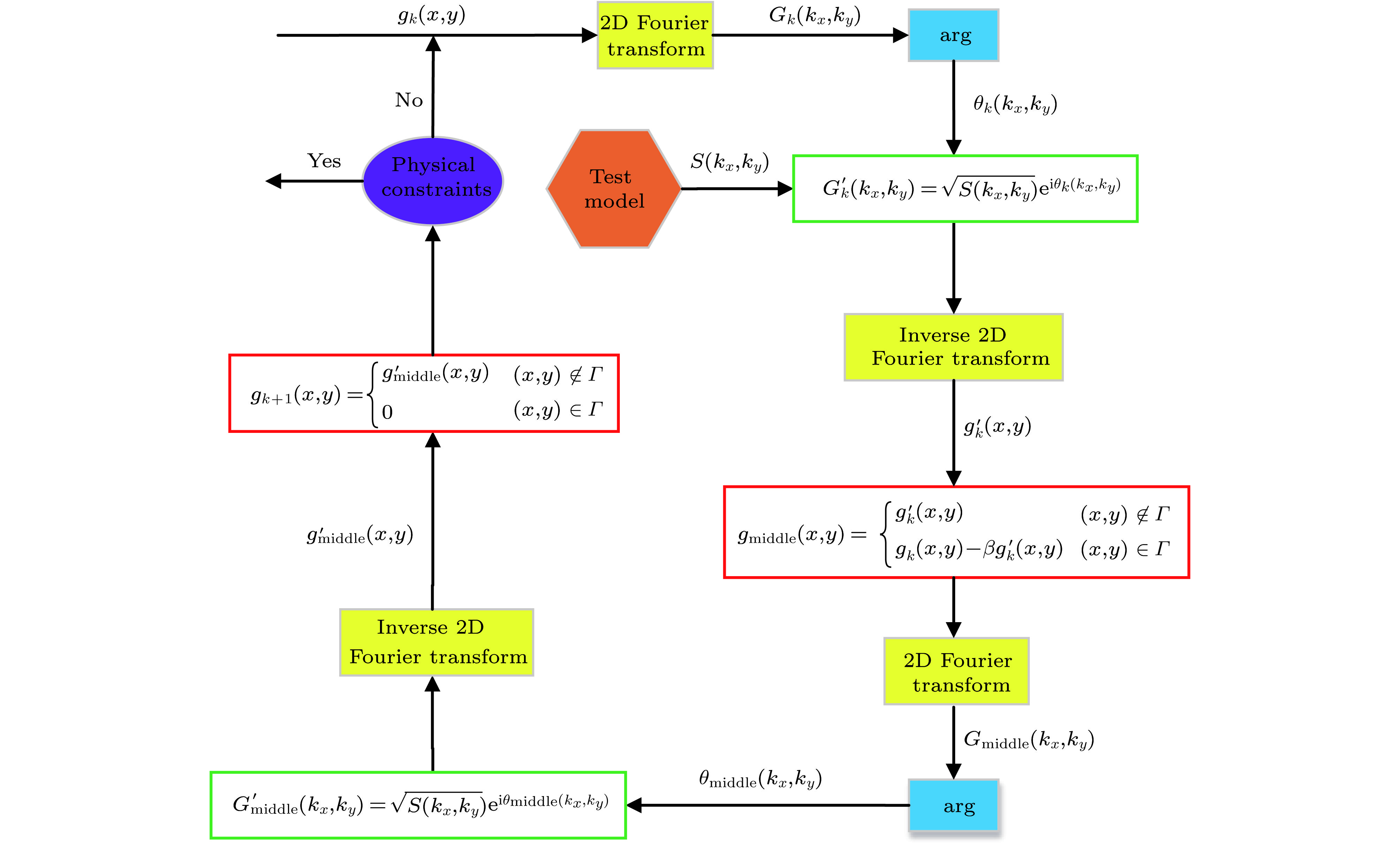
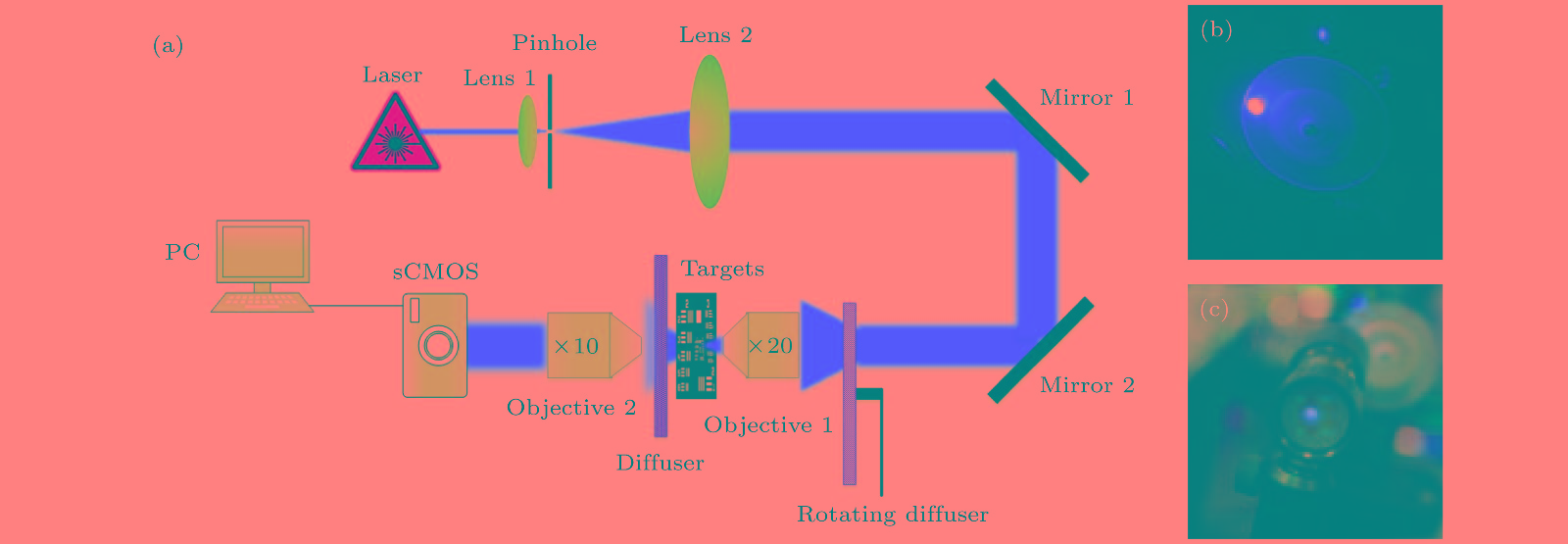
-
Scattering in medium is a serious problem that limits the imaging depth or imaging distance. According to the absorption and scattering of light in biological tissues, it is difficult for both excited light and signal light to penetrate biological tissues, and the scattering effect in biological tissues will destroy the phase information of signal light, so it is difficult to directly carry out high resolution imaging in deep biological tissues. In the recent studies it is surprisingly found that two-dimensional image information of an object can be directly recovered from the disordered speckle pattern with pseudothermal light sources based on the optical memory effect (ME) and autocorrelation (AC) method. In this paper, we study a speckle imaging method based on pseudothermal illumination, where the Gerchberg-Saxton algorithm is used to perform the phase recovery of the object. Here, the advantages and disadvantages of HIO&ER algorithm and ping-pang (PP) algorithm based on the ME and AC method for imaging through random scattering medium are compared by using numerical simulation. By comparing the recovery effects and the numbers of iterations between HIO&ER algorithm and PP algorithm, it is found that PP algorithm has a fast running speed when a higher recovery quality is maintained. In addition, a continuous He-Ne laser and rotating ground glass are used to produce a pseudothermal light source. And a single frame imaging of different shape objects, which are a few millimeters away from random scattering medium, is carried out by objective lens. Then PP algorithm is adopted to recover the actual image of micron object. Furthermore, we experimentally find that the magnification, resolution and image intensity, which are qualitatively studied, are seriously affected by the distance between the focal plane of the object lens and scattering medium. We find that with the increase of the distance, the obtained autocorrelation graph and retrieval graph have corresponding amplification and the object sampling point information collected on sCOMS increases, which improves its resolution. However, the scattered light intensity collected by objective lens decreases after passing through the scattering medium, making the intensity of recovered image weaken. The results of this study will further promote the application of ME and AC method in the study of deep tissue medical imaging.
[1] Ntziachristos V 2010 Nat. Meth. 7 603
Google Scholar
[2] Hoffman R M 2008 Methods Cell Biol. 85 485
Google Scholar
[3] Yang X, Pu Y, Psaltis D 2014 Opt. Express 22 3405
Google Scholar
[4] Kang S, Jeong S, Choi W, Ko H, Yang T D, Joo J H, Lee J S, Lim Y S, Park Q H, Choi W 2015 Nat. Photon. 9 253
Google Scholar
[5] Bertolotti J, van Putten E G, Blum C, Lagendijk A, Vos W L, Mosk A P 2012 Nature 491 232
Google Scholar
[6] Wu T, Dong J, Shao X, Gigan S 2017 Opt. Express 25 27182
Google Scholar
[7] Sudarsanam S, Mathew J, Panigrahi S, Fade J, Alouini M, Ramachandran H 2016 Sci. Rep. 6 25033
Google Scholar
[8] Zhuang X W 2009 Nat. Photon. 3 436
Google Scholar
[9] Kolenderska S M, Katz O, Fink M, Gigan S 2015 Opt. Lett. 40 534
Google Scholar
[10] Vellekoop I M, Mosk A P 2007 Opt. Lett. 32 2309
Google Scholar
[11] Katz O, Small E, Guan Y, Silberberg Y 2014 Optica 1 170
Google Scholar
[12] He G S 2002 Prog. Quantum Electron. 26 131
Google Scholar
[13] Lai P, Xu X, Liu H, Suzuki Y, Wang L V 2011 J. Biomed. Opt. 16 080505
Google Scholar
[14] Xu X, Liu H, Wang L V 2011 Nat. Photon. 5 154
Google Scholar
[15] Li X H, Deng C J, Chen M L, Gong W L, Han S S 2011 Opt. Lett. 36 394
Google Scholar
[16] Devaux F, Huy K P, Denis S, Lantz E, Moreau P A 2017 J. Opt. 19 024001
Google Scholar
[17] Moreau P A, Toninelli E, Gregory T, Padgett M J 2018 Laser Photon. Rev. 12 1863
Google Scholar
[18] Takasaki K T, Fleischer J W 2014 Opt. Express 22 31426
Google Scholar
[19] Schott S, Bertolotti J, Leger J F, Bourdieu L, Gigan S 2015 Opt. Express 23 13505
Google Scholar
[20] Edrei E, Scarcelli G 2016 Sci. Rep. 6 33558
Google Scholar
[21] Berto P, Rigneault H, Guillon M 2017 Opt. Lett. 42 5117
Google Scholar
[22] Osnabrugge G, Horstmeyer R, Papadopoulos I N, Judkewitz B, Vellekoop I M 2017 Optica 4 886
Google Scholar
[23] Katz O, Heidmann P, Fink M, Gigan S 2014 Nat. Photon. 8 784
Google Scholar
[24] Judkewitz B, Horstmeyer R, Vellekoop I M, Papadopoulos I N, Yang C 2015 Nat. Phys. 11 684
Google Scholar
[25] Amir P, Ravn A E, Hervé R, Dan O, Sylvain G, Ori K 2016 Opt. Express 24 16835
Google Scholar
[26] Wang W, Hu X, Liu J, Zhang S, Suo J, Situ G 2015 Opt. Express 23 28416
Google Scholar
[27] Thrane L, Yura H T, Andersen P E 2000 J. Opt. Soc. Am. A 17 484
Google Scholar
[28] Antipov S P, Bogdashov A A, Chirkov A V, Denisov G G 2003 Int. J. Infrared Millimeter waves 24 1677
Google Scholar
[29] 范爽, 张亚萍, 王帆, 高云龙, 钱晓凡, 张永安, 许蔚, 曹良才 2018 67 094203
Google Scholar
Fan S, Zhang Y P, Wang F, Gao Y L, Qian X F, Zhang Y A, Xu W, Cao L C 2018 Acta Phys. Sin. 67 094203
Google Scholar
[30] Fienup J R 1982 Appl. Opt. 21 2758
Google Scholar
[31] Michelle C, Haojiang Z E, Changhuei Y 2017 Opt. Express 25 3935
Google Scholar
[32] Shi Y, Liu Y, Wang J, Wu T 2017 Appl. Phys. Lett. 110 231101
Google Scholar
[33] Hofer M, Soeller C, Brasselet S, Bertolotti J 2018 Opt. Express 26 9866
Google Scholar
-
图 1 散斑产生示意图
Figure 1. Schematic of speckle generation.
图 2 相位恢复算法框图
Figure 2. Schematic of phase retrieval algorithm.
图 3 成像过程的数值模拟 (a) 物体; (b) 点扩散函数; (c) 散斑图; (d) 点扩散函数AC; (e) 物体AC; (f) 散斑AC; (g) 能量谱开根; (h) 重建结果
Figure 3. Simulations of imaging process: (a) Object; (b) point diffusion function; (c) speckle pattern; (d) AC of point diffusion function; (e) AC of object; (f) AC of speckle pattern; (g) square root of power spectrum; (h) result of reconstruction.
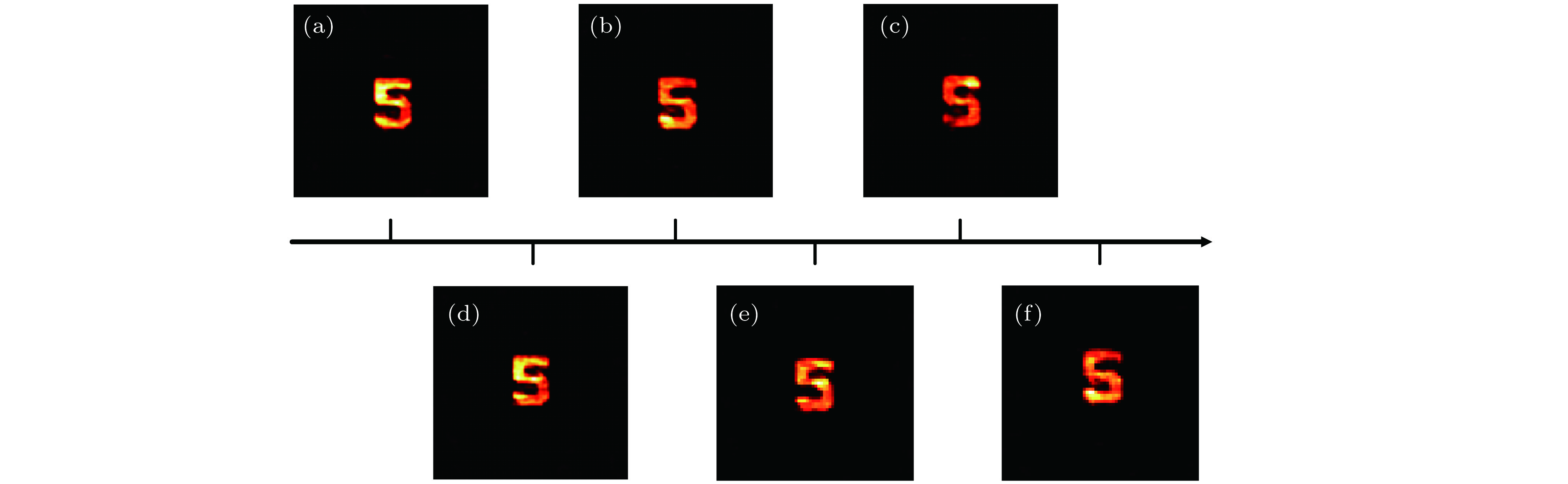
图 4 不同迭代次数下的恢复效果 (a)—(c) HIO&ER算法的恢复结果, 其中, (a)
$\beta = 1: - 0.02:0$ , (b)$\beta = 1: - 0.04:0$ , (c)$\beta = 1: - 0.05:0$ ; (d)—(f) PP算法的恢复结果, 其中, (d)$\beta = 3: - 0.02:1$ , (e)$\beta = 3: - 0.05:1$ , (f)$\beta = 3: - 0.1:1$ Figure 4. Retrieval results in different interation times: (a)−(c) Retrieval results of HIO&ER algorithm when (a)
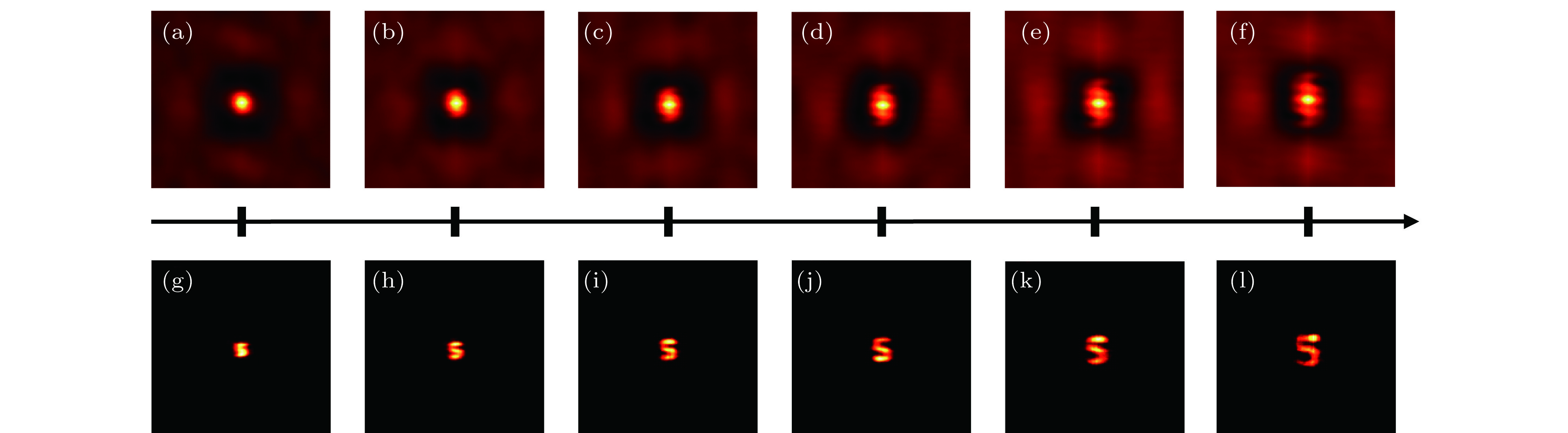
$\beta = 1: - 0.02:0$ , (b)$\beta = 1: - 0.04:0$ , (c)$\beta = 1: - 0.05:0$ ; (d)−(f) Retrieval results of PP algorithm when (d)$\beta = 3: - 0.02:1$ , (e)$\beta = 3: - 0.05:1$ , (f)$\beta = 3: - 0.1:1$ .
图 5 通过散射介质成像的光学装置 (a)实验光路图; (b)赝热光的产生; (c)散斑的产生
Figure 5. Optical setups used for imaging through the scattering media: (a) Optical path in experiment; (b) generation of pseudothermal light source; (c) generation of speckle pattern.
图 6 不同数字的实验结果 (a)—(e)数字“1”的恢复过程, 其中, (a)物体, (b) sCOMS成像, (c)散斑AC, (d)能量谱开根, (e)重建结果; (f)—(t)数字“3”, “5”, “6”的恢复过程
Figure 6. Experimental results for different numbers: (a)−(e) Retrieval process of number “1”, namely, (a) object, (b) sCOMS image, (c) autocorrelaction of speckle pattern, (d) square root of power spectrum, (e) result of reconstruction; (f)−(t) retrieval processes of number “3”, “5” and “6”.
图 7 不同物镜和散射介质间距对成像效果的影响 (a)—(f)不同间距下的散斑AC结果; (g)—(l)不同间距下的恢复结果
Figure 7. Effects of different distance between objective and diffuser: (a)−(f) AC results of speckle pattern in different distance; (g)−(l) retrieval results in different distance.
表 1 不同情形下算法迭代次数
Table 1. Interation times of algorithm in different conditions.
Algorithm Physical
contraint NPhysical
contraint $\beta$Interation
timesHIO&ER 30 $1: - 0.02:0$ 1560 30 $1: - 0.04:0$ 810 30 $1: - 0.05:0$ 660 PP 30 $3: - 0.02:1$ 202 30 $3: - 0.05:1$ 82 30 $3: - 0.1:1$ 42 
DownLoad: CSV
-
[1] Ntziachristos V 2010 Nat. Meth. 7 603
Google Scholar
[2] Hoffman R M 2008 Methods Cell Biol. 85 485
Google Scholar
[3] Yang X, Pu Y, Psaltis D 2014 Opt. Express 22 3405
Google Scholar
[4] Kang S, Jeong S, Choi W, Ko H, Yang T D, Joo J H, Lee J S, Lim Y S, Park Q H, Choi W 2015 Nat. Photon. 9 253
Google Scholar
[5] Bertolotti J, van Putten E G, Blum C, Lagendijk A, Vos W L, Mosk A P 2012 Nature 491 232
Google Scholar
[6] Wu T, Dong J, Shao X, Gigan S 2017 Opt. Express 25 27182
Google Scholar
[7] Sudarsanam S, Mathew J, Panigrahi S, Fade J, Alouini M, Ramachandran H 2016 Sci. Rep. 6 25033
Google Scholar
[8] Zhuang X W 2009 Nat. Photon. 3 436
Google Scholar
[9] Kolenderska S M, Katz O, Fink M, Gigan S 2015 Opt. Lett. 40 534
Google Scholar
[10] Vellekoop I M, Mosk A P 2007 Opt. Lett. 32 2309
Google Scholar
[11] Katz O, Small E, Guan Y, Silberberg Y 2014 Optica 1 170
Google Scholar
[12] He G S 2002 Prog. Quantum Electron. 26 131
Google Scholar
[13] Lai P, Xu X, Liu H, Suzuki Y, Wang L V 2011 J. Biomed. Opt. 16 080505
Google Scholar
[14] Xu X, Liu H, Wang L V 2011 Nat. Photon. 5 154
Google Scholar
[15] Li X H, Deng C J, Chen M L, Gong W L, Han S S 2011 Opt. Lett. 36 394
Google Scholar
[16] Devaux F, Huy K P, Denis S, Lantz E, Moreau P A 2017 J. Opt. 19 024001
Google Scholar
[17] Moreau P A, Toninelli E, Gregory T, Padgett M J 2018 Laser Photon. Rev. 12 1863
Google Scholar
[18] Takasaki K T, Fleischer J W 2014 Opt. Express 22 31426
Google Scholar
[19] Schott S, Bertolotti J, Leger J F, Bourdieu L, Gigan S 2015 Opt. Express 23 13505
Google Scholar
[20] Edrei E, Scarcelli G 2016 Sci. Rep. 6 33558
Google Scholar
[21] Berto P, Rigneault H, Guillon M 2017 Opt. Lett. 42 5117
Google Scholar
[22] Osnabrugge G, Horstmeyer R, Papadopoulos I N, Judkewitz B, Vellekoop I M 2017 Optica 4 886
Google Scholar
[23] Katz O, Heidmann P, Fink M, Gigan S 2014 Nat. Photon. 8 784
Google Scholar
[24] Judkewitz B, Horstmeyer R, Vellekoop I M, Papadopoulos I N, Yang C 2015 Nat. Phys. 11 684
Google Scholar
[25] Amir P, Ravn A E, Hervé R, Dan O, Sylvain G, Ori K 2016 Opt. Express 24 16835
Google Scholar
[26] Wang W, Hu X, Liu J, Zhang S, Suo J, Situ G 2015 Opt. Express 23 28416
Google Scholar
[27] Thrane L, Yura H T, Andersen P E 2000 J. Opt. Soc. Am. A 17 484
Google Scholar
[28] Antipov S P, Bogdashov A A, Chirkov A V, Denisov G G 2003 Int. J. Infrared Millimeter waves 24 1677
Google Scholar
[29] 范爽, 张亚萍, 王帆, 高云龙, 钱晓凡, 张永安, 许蔚, 曹良才 2018 67 094203
Google Scholar
Fan S, Zhang Y P, Wang F, Gao Y L, Qian X F, Zhang Y A, Xu W, Cao L C 2018 Acta Phys. Sin. 67 094203
Google Scholar
[30] Fienup J R 1982 Appl. Opt. 21 2758
Google Scholar
[31] Michelle C, Haojiang Z E, Changhuei Y 2017 Opt. Express 25 3935
Google Scholar
[32] Shi Y, Liu Y, Wang J, Wu T 2017 Appl. Phys. Lett. 110 231101
Google Scholar
[33] Hofer M, Soeller C, Brasselet S, Bertolotti J 2018 Opt. Express 26 9866
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9114
- PDF Downloads: 126
- Cited By: 0
