-
非晶态合金在非晶态形成过程中呈现出复杂的动力学行为, 理解非晶态合金及其过冷熔体的动力学规律是非晶态研究领域的重要内容. 从拓扑序的角度去重新审视非晶态系统的动力学行为为深入理解非晶态及非晶态转变的物理本质提供了一个全新的视角. 本文采用分子动力学模拟方法研究了CuZr合金熔体在非晶态转变中的微观动力学特征. 模拟发现, 在原子的位移矢量场中出现大量的涡旋结构, 涡旋形成率在非晶态转变温度附近出现不连续降低. 涡旋伴随着高应变事件的发生, 两者的形成率之间存在特征比值, 而在涡旋态转变前后该比值加倍. 分析认为, 观察到的涡旋态转变具有拓扑相变的特征, 即在非晶合金熔体的位移矢量场中存在拓扑相变. 涡旋及相伴产生的高应变事件与非晶合金熔体中的各种次级弛豫有着密切的关系. 本文为理解和揭示非晶态转变过程中复杂动力学行为的物理本质提供了一个新的切入点.Metallic glass-forming systems exhibit complex dynamic behaviors during the glass transition. Understanding the dynamic nature of metallic glasses and supercooled liquids is a crucial issue in the study of glassy physics. Topological order provides a novel perspective for re-examining the dynamics of glassy systems and elucidating the physical essence of the glassy state and glass transition. In this study, the microscopic dynamics of CuZr melts in the glass transition are investigated using molecular dynamics simulations. The single-particle dynamic characteristics in the supercooled CuZr melt are the random jump motions of atoms after a long-term caging period. To capture these dynamics, the displacement vector field is constructed based on the spatiotemporal distribution of these jump events. The simulation results reveal that there exist the numerous vortex structures in the displacement vector field. Notably, the vortex formation rate, which is defined as the number of vortices generated per unit time, exhibits a sharp drop near the glass transition temperature. The probability distribution of vortex formation rate displays a bimodal pattern on the drops, indicating the coexistence of two different dynamical states related to vortex formation. Multiple high-strain events are observed surrounding these vortices. It is found that the two vortex states during the transition exhibit markedly different characteristic ratios of vortices to high-strain events (1∶4 vs 1∶8), indicating a change in the coupling strength between vortex formation and high-strain activity. The high-strain events predominantly form in the regions between positive and negative vortices, and the specific quantitative relationship between vortices and high-strain events indirectly reflects the presence of strongly interacting vortex-antivortex pairs in the melt. During the vortex state transition, the vortex-to-high-strain-event ratio suddenly doubles, which means that this transition is not only a sudden change in the rate of vortex formation, but also an enhancement of the interactions between vortex-antivortex pairs, representing a change in global topological properties. These findings demonstrate that the vortex transition exhibits the characteristics of a topological phase transition, thereby predicting the existence of a topological phase transition in the displacement vector field of metallic glass-forming systems. Further speculation suggests that vortices and high-strain events are related to multiple secondary relaxation processes. This study provides a new perspective for understanding the dynamics of glass-forming systems and the glass transition.
-
Keywords:
- topological phase transition /
- metallic glass /
- vortex /
- displacement vector field
[1] Klement W, Willens R, Duwez P 1960 Nature 187 869
 Google Scholar
Google Scholar
[2] Bernal J D 1959 Nature 183 141
 Google Scholar
Google Scholar
[3] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
 Google Scholar
Google Scholar
[4] Finney J L 1970 Proc. Roy. Soc. Lond. A 319 479
 Google Scholar
Google Scholar
[5] Miracle D B 2004 Nat. Mater. 3 697
 Google Scholar
Google Scholar
[6] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
 Google Scholar
Google Scholar
[7] Frank F C 1952 Proc. R. Soc. Lond. A 215 43
 Google Scholar
Google Scholar
[8] Hirata A, Kang L J, Fujita T, Klumov B, Matsue K, Kotani M, Yavari A R, Chen M W 2013 Science 341 376
 Google Scholar
Google Scholar
[9] 李茂枝 2017 66 176107
 Google Scholar
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
 Google Scholar
Google Scholar
[10] 蒋元祺, 彭平 2018 67 132101
 Google Scholar
Google Scholar
Jiang Y Q, Peng P 2018 Acta Phys. Sin. 67 132101
 Google Scholar
Google Scholar
[11] Wu C, Huang Y J, Shen J 2013 Chin. Phys. Lett. 30 106102
 Google Scholar
Google Scholar
[12] Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501
 Google Scholar
Google Scholar
[13] Lü Y J, Entel P 2011 Phys. Rev. B 84 104203
 Google Scholar
Google Scholar
[14] Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6053
 Google Scholar
Google Scholar
[15] Neophytou A, Chakrabarti D, Sciortino F 2022 Nat. Phys. 18 1248
 Google Scholar
Google Scholar
[16] Berezinskii V L 1971 Sov. Phys. JETP 32 493
[17] Kosterlitz J M, Thouless D J 1973 J. Phys. C: Solid State Phys. 6 1181
 Google Scholar
Google Scholar
[18] Kosterlitz J M 2016 Rep. Prog. Phys. 79 026001
 Google Scholar
Google Scholar
[19] DiDonna B A, Lubensky T C 2005 Phys. Rev. E 72 066619
 Google Scholar
Google Scholar
[20] Del Gado E, Ilg P, Kroeger M, Oettinger H C 2008 Phys. Rev. Lett. 101 095501
 Google Scholar
Google Scholar
[21] Dasgupta R, Hentschel H G E, Procaccia I 2012 Phys. Rev. Lett. 109 255502
 Google Scholar
Google Scholar
[22] Wu Z W, Chen Y, Wang W H, Kob W, Xu L 2023 Nature Commun. 14 2955
 Google Scholar
Google Scholar
[23] Lü Y J, Guo C C, Huang H S, Gao J A, Qin H R, Wang W H 2021 Acta Mater. 211 116873
 Google Scholar
Google Scholar
[24] Lü Y J, Qin H R, Guo C C 2021 Phys. Rev. B 104 224103
 Google Scholar
Google Scholar
[25] Tang M B, Zhao D Q, Pan M X, Wang W H 2004 Chin. Phys. Lett. 21 901
 Google Scholar
Google Scholar
[26] Mendelev M I, Kramer M J, Ott R T, Sordelet D J, Yagodin D, Popel P 2009 Philos. Mag. 89 967
 Google Scholar
Google Scholar
[27] Nosé S 1984 J. Chem. Phys. 81 511
 Google Scholar
Google Scholar
[28] Hoover W G 1985 Phys. Rev. A 31 1695
 Google Scholar
Google Scholar
[29] Plimpton S 1995 J. Comp. Phys. 117 1
 Google Scholar
Google Scholar
[30] Chou C F, Jin A J, Hui S W, Huang C C, Ho J T 1998 Science 280 1424
 Google Scholar
Google Scholar
[31] Mirkovic J, Savel’ev S E, Sugahara E, Kadowaki K 2001 Phys. Rev. Lett. 86 886
 Google Scholar
Google Scholar
[32] Kim S, Hu C R, Andrews M J 2004 Phys. Rev. B 69 094521
 Google Scholar
Google Scholar
-
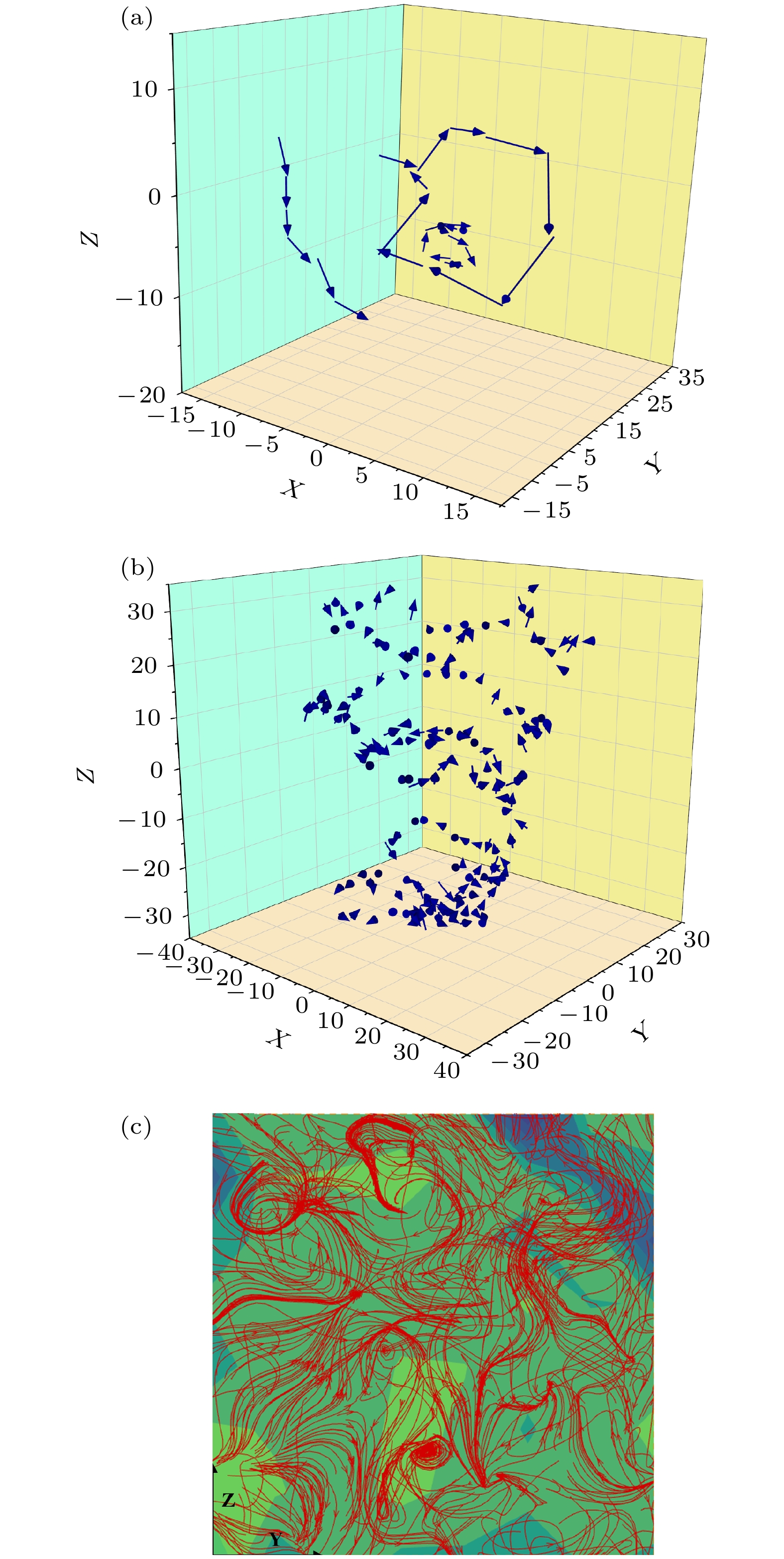
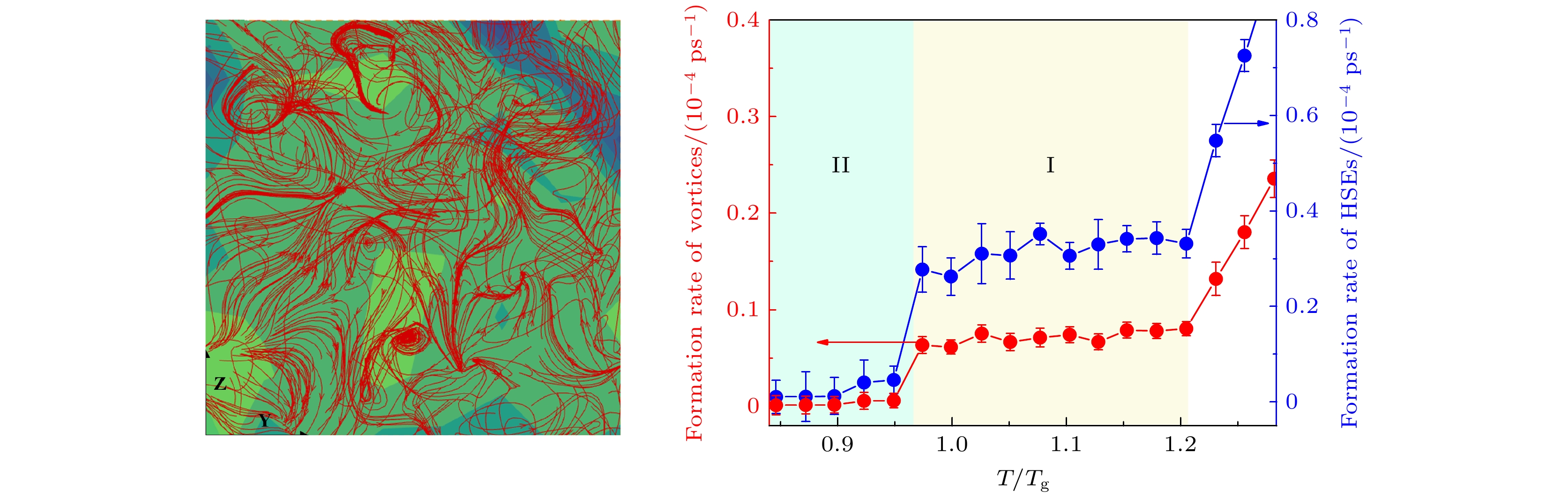
图 3 CuZr过冷合金熔体中原子“跳跃”运动的空间构型 (a)在较短的观察时间内观察到弦链状或环状结构; (b)在较长观察时间内观察到的涡旋结构; (c)位移矢量流场在X方向上的一个剖面, 可以观察到由大量涡旋构成的涡旋阵列
Fig. 3. Spatial configuration of jump motions of atoms in supercooled CuZr melt: (a) String- and loop-like configurations observed in a short time interval; (b) vortex that is observed in a relatively long time; (c) a cross section of the flow field of atomic displacements along the X direction, which shows a disordered vortex lattice composed of vortices.
-
[1] Klement W, Willens R, Duwez P 1960 Nature 187 869
 Google Scholar
Google Scholar
[2] Bernal J D 1959 Nature 183 141
 Google Scholar
Google Scholar
[3] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
 Google Scholar
Google Scholar
[4] Finney J L 1970 Proc. Roy. Soc. Lond. A 319 479
 Google Scholar
Google Scholar
[5] Miracle D B 2004 Nat. Mater. 3 697
 Google Scholar
Google Scholar
[6] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
 Google Scholar
Google Scholar
[7] Frank F C 1952 Proc. R. Soc. Lond. A 215 43
 Google Scholar
Google Scholar
[8] Hirata A, Kang L J, Fujita T, Klumov B, Matsue K, Kotani M, Yavari A R, Chen M W 2013 Science 341 376
 Google Scholar
Google Scholar
[9] 李茂枝 2017 66 176107
 Google Scholar
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
 Google Scholar
Google Scholar
[10] 蒋元祺, 彭平 2018 67 132101
 Google Scholar
Google Scholar
Jiang Y Q, Peng P 2018 Acta Phys. Sin. 67 132101
 Google Scholar
Google Scholar
[11] Wu C, Huang Y J, Shen J 2013 Chin. Phys. Lett. 30 106102
 Google Scholar
Google Scholar
[12] Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501
 Google Scholar
Google Scholar
[13] Lü Y J, Entel P 2011 Phys. Rev. B 84 104203
 Google Scholar
Google Scholar
[14] Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6053
 Google Scholar
Google Scholar
[15] Neophytou A, Chakrabarti D, Sciortino F 2022 Nat. Phys. 18 1248
 Google Scholar
Google Scholar
[16] Berezinskii V L 1971 Sov. Phys. JETP 32 493
[17] Kosterlitz J M, Thouless D J 1973 J. Phys. C: Solid State Phys. 6 1181
 Google Scholar
Google Scholar
[18] Kosterlitz J M 2016 Rep. Prog. Phys. 79 026001
 Google Scholar
Google Scholar
[19] DiDonna B A, Lubensky T C 2005 Phys. Rev. E 72 066619
 Google Scholar
Google Scholar
[20] Del Gado E, Ilg P, Kroeger M, Oettinger H C 2008 Phys. Rev. Lett. 101 095501
 Google Scholar
Google Scholar
[21] Dasgupta R, Hentschel H G E, Procaccia I 2012 Phys. Rev. Lett. 109 255502
 Google Scholar
Google Scholar
[22] Wu Z W, Chen Y, Wang W H, Kob W, Xu L 2023 Nature Commun. 14 2955
 Google Scholar
Google Scholar
[23] Lü Y J, Guo C C, Huang H S, Gao J A, Qin H R, Wang W H 2021 Acta Mater. 211 116873
 Google Scholar
Google Scholar
[24] Lü Y J, Qin H R, Guo C C 2021 Phys. Rev. B 104 224103
 Google Scholar
Google Scholar
[25] Tang M B, Zhao D Q, Pan M X, Wang W H 2004 Chin. Phys. Lett. 21 901
 Google Scholar
Google Scholar
[26] Mendelev M I, Kramer M J, Ott R T, Sordelet D J, Yagodin D, Popel P 2009 Philos. Mag. 89 967
 Google Scholar
Google Scholar
[27] Nosé S 1984 J. Chem. Phys. 81 511
 Google Scholar
Google Scholar
[28] Hoover W G 1985 Phys. Rev. A 31 1695
 Google Scholar
Google Scholar
[29] Plimpton S 1995 J. Comp. Phys. 117 1
 Google Scholar
Google Scholar
[30] Chou C F, Jin A J, Hui S W, Huang C C, Ho J T 1998 Science 280 1424
 Google Scholar
Google Scholar
[31] Mirkovic J, Savel’ev S E, Sugahara E, Kadowaki K 2001 Phys. Rev. Lett. 86 886
 Google Scholar
Google Scholar
[32] Kim S, Hu C R, Andrews M J 2004 Phys. Rev. B 69 094521
 Google Scholar
Google Scholar
计量
- 文章访问数: 400
- PDF下载量: 13
- 被引次数: 0













 下载:
下载: