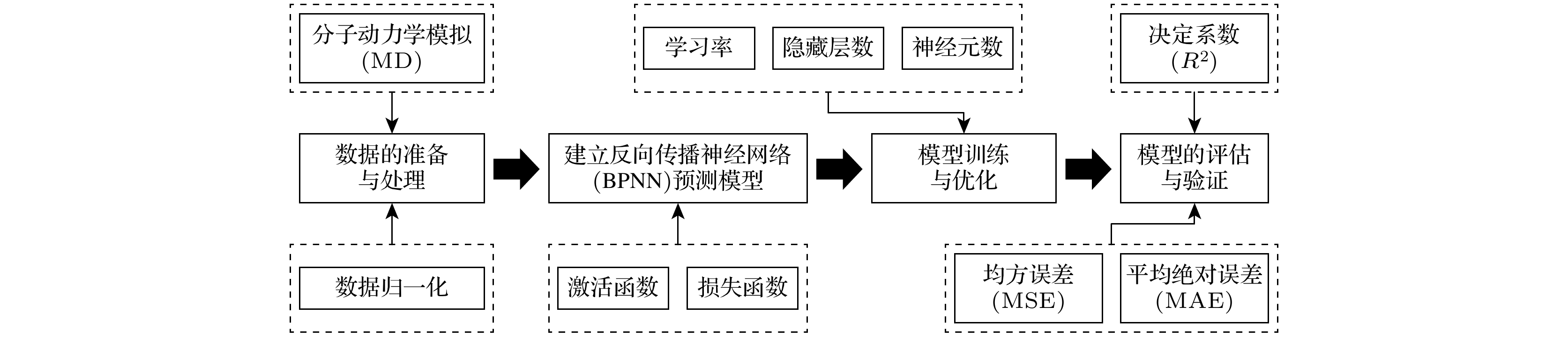
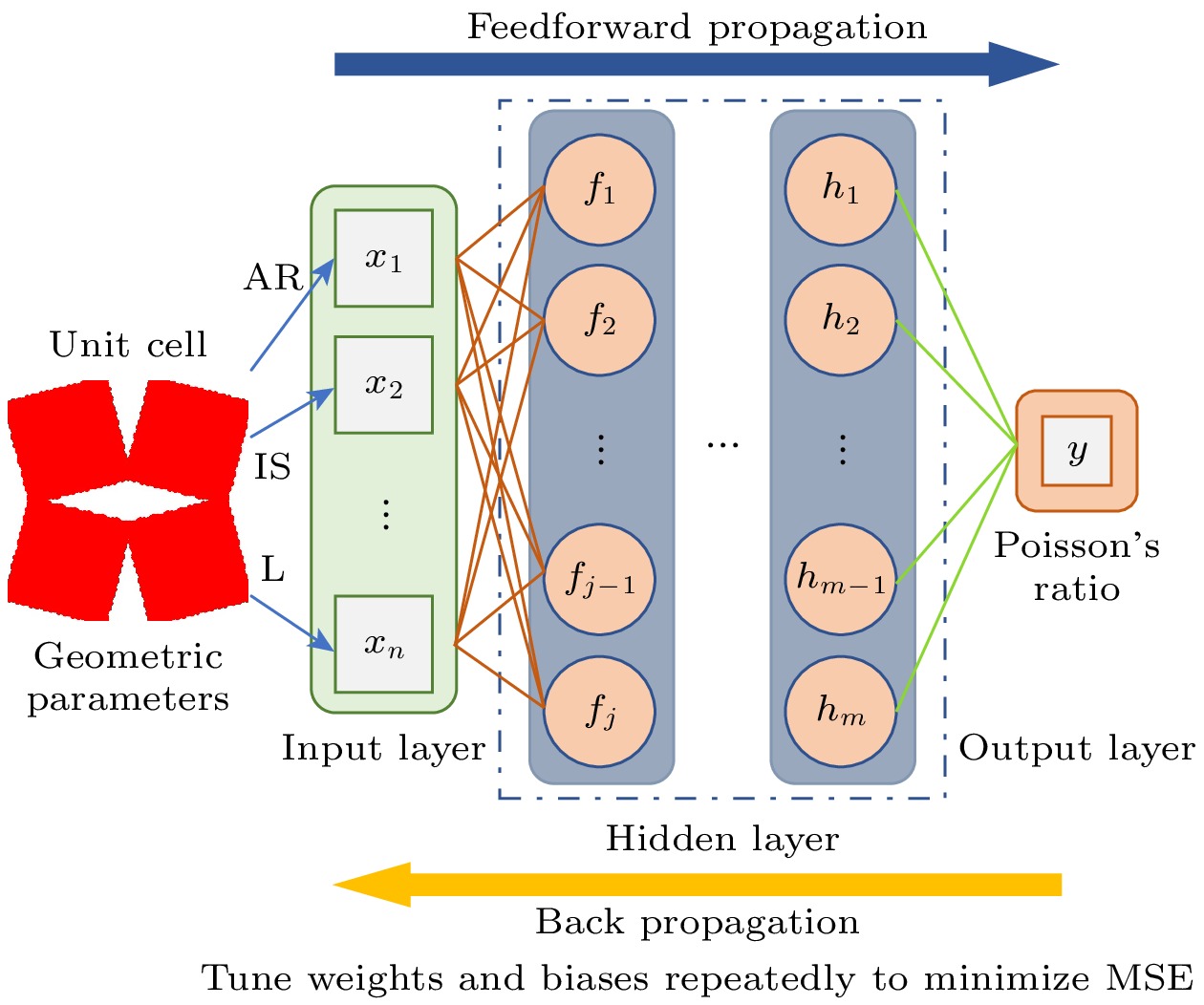
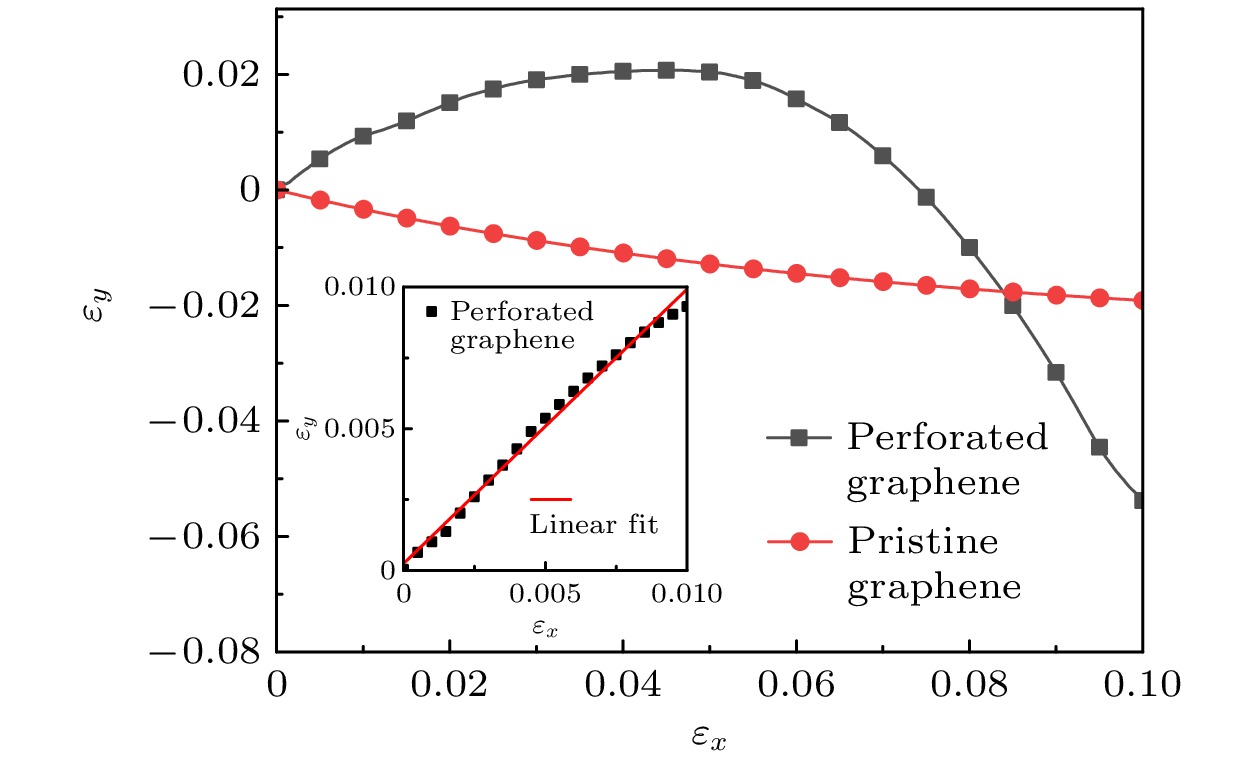
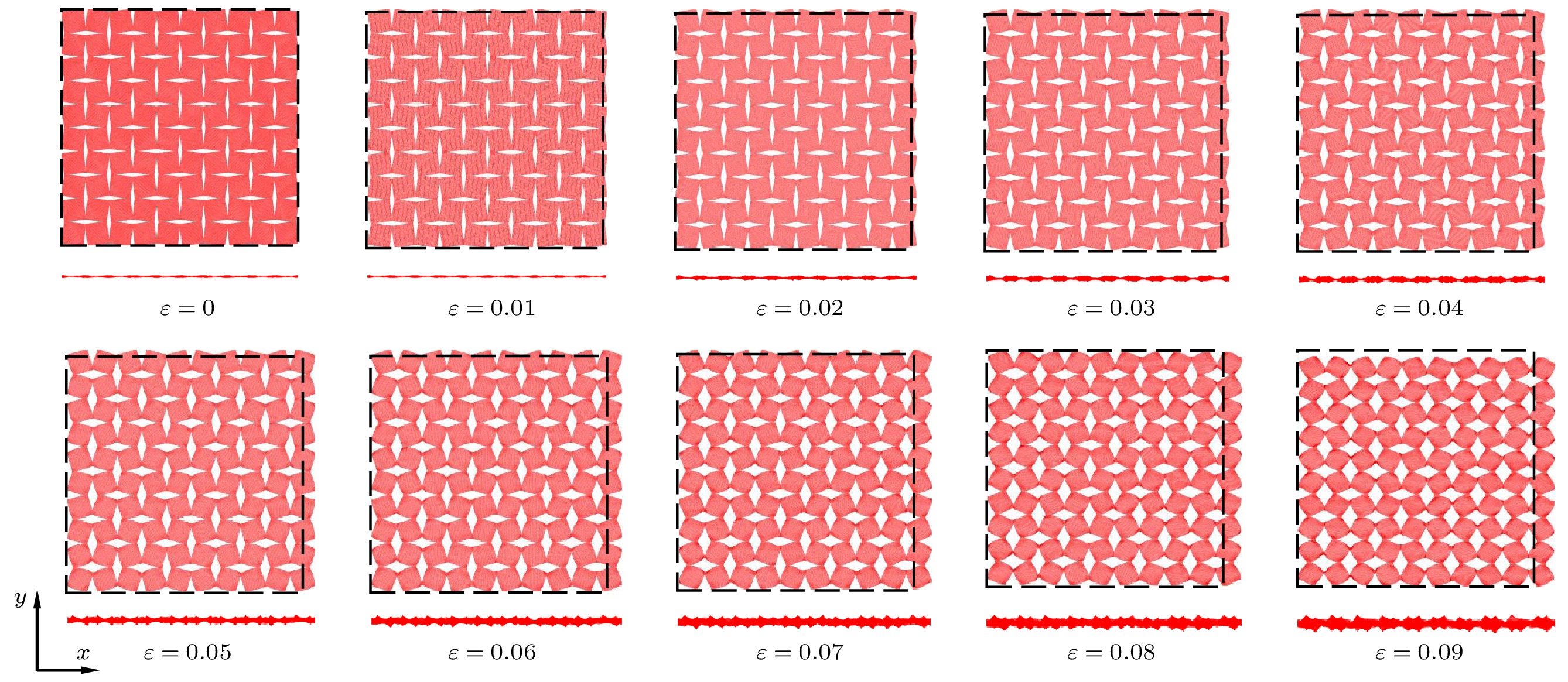
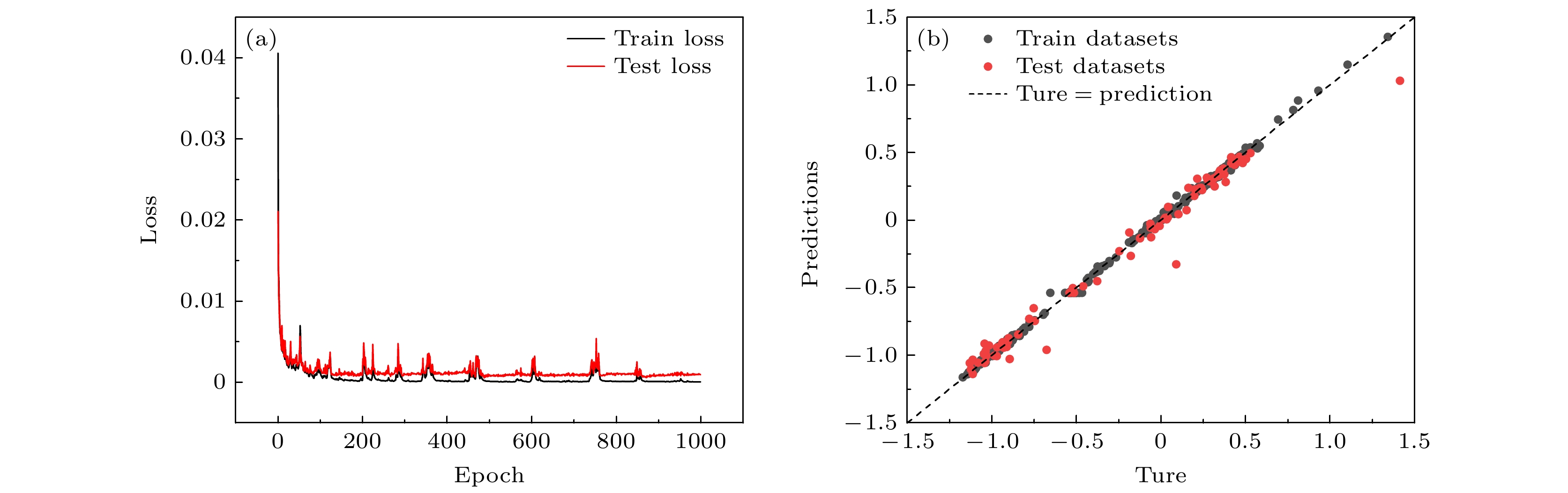
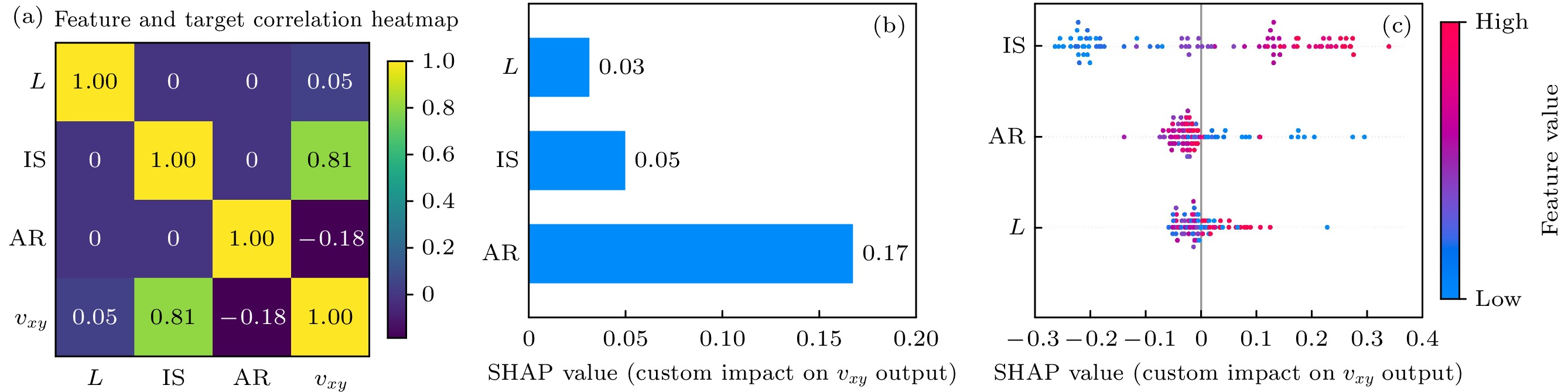
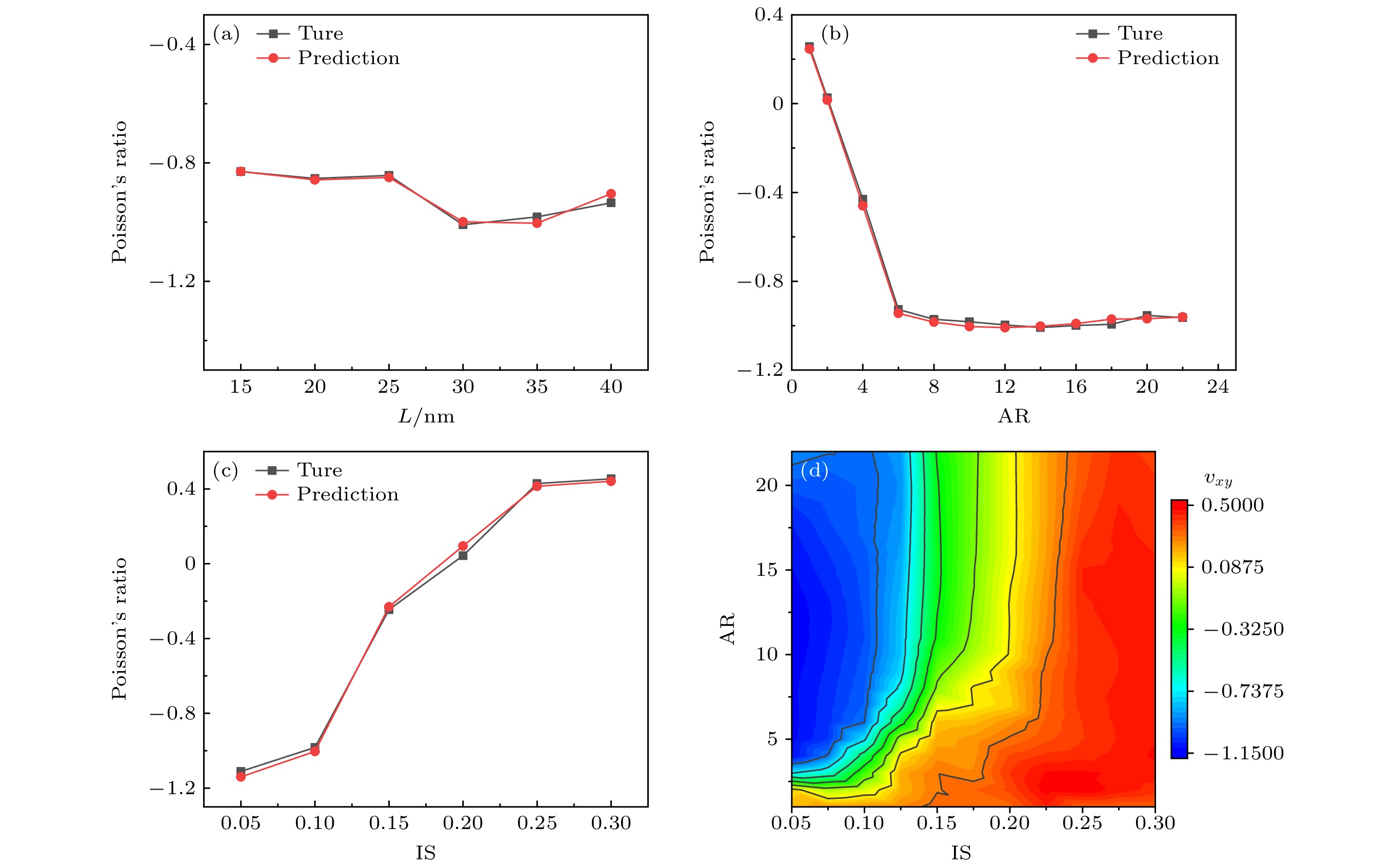
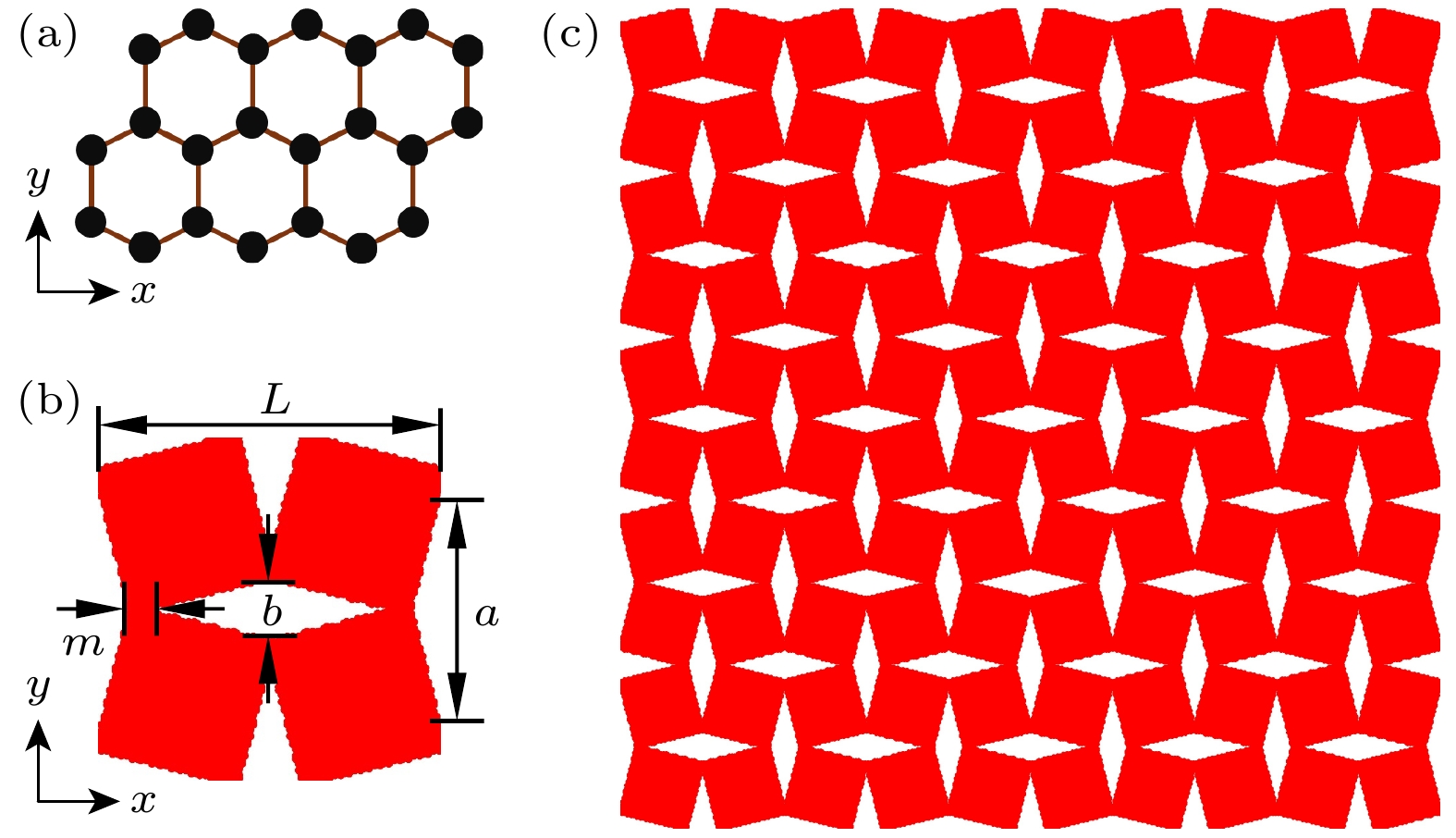
-
通过结构设计调控石墨烯的性能已引起广泛关注. 然而, 结构设计几何参数与性能之间存在复杂的非线性关系, 如何准确预测石墨烯性能参数加快结构设计仍需进一步深入探索. 本文通过引入周期性菱形穿孔缺陷有效地实现了负泊松比石墨烯的结构设计, 分析了负泊松比效应的产生机制, 并基于反向传播神经网络(BPNN)构建了一种数据驱动的机器学习模型, 可实现高效预测并设计具有负泊松比的穿孔石墨烯结构. 通过分子动力学模拟构建菱形穿孔石墨烯结构的泊松比数据集, 采用优化后的BPNN模型对泊松比进行预测分析, 研究发现, 穿孔间距比(IS)对菱形穿孔石墨烯结构泊松比的影响最显著, 而穿孔纵横比(AR)与晶胞尺寸(L)的影响则相对较弱. 本文还研究了不同穿孔几何参数对菱形穿孔石墨烯负泊松比效应的影响规律, 减小IS和增大AR能够增强石墨烯结构的负泊松比效应. 机器学习模型的预测结果与分子动力学模拟结果高度吻合, 验证了机器学习方法在石墨烯泊松比预测中的有效性和可靠性. 本研究通过引入菱形穿孔缺陷, 结合机器学习技术, 实现对石墨烯负泊松比效应的高效预测与优化, 为其在智能材料和柔性电子中的应用提供理论支持.Tuning graphene’s properties through structural design has received significant attention. However, the complex nonlinear relationship between geometric parameters of structural design and performance needs further exploring to accurately predict the performance of graphene and speed up the optimization of its structural design. This study introduces periodic rhombic perforations to effectively achieve the structural design of graphene with negative Poisson’s ratio (NPR). The mechanisms underlying the NPR effect are analyzed, and a data-driven machine learning model based on a backpropagation neural network (BPNN) is developed to efficiently predict and design perforated graphene structures exhibiting NPR. By constructing a Poisson’s ratio dataset for rhombic perforated graphene structures through molecular dynamics simulations and employing an optimized BPNN model for predictive analysis, it is found that the perforation spacing ratio (IS) has the most significant effect on the Poisson’s ratio of rhombic perforated graphene, while the perforation aspect ratio (AR) and unit cell size (L) have relatively weak influence. The study further investigates the influence of various perforation geometric parameters on the NPR behavior of graphene. It is found that reducing IS and increasing AR can enhance the negative Poisson’s ratio effect. The machine learning predictions closely align with molecular dynamics simulation results, demonstrating the effectiveness and reliability of this approach for Poisson’s ratio prediction. By integrating rhombic perforation design with machine learning technologies, this research provides an efficient framework for optimizing the NPR effect in graphene, and theoretical support for its application in smart materials and flexible electronics.
-
Keywords:
- graphene /
- negative Poisson’s ratio /
- machine learning /
- molecular dynamics
[1] Lee C, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[2] Zhang Y B, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Balandin A A, Ghosh S, Bao W Z, Calizo I, Teweldebrhan D, Miao F, Lau C N 2008 Nano Lett. 8 902
Google Scholar
[5] Jang H, Park Y J, Chen X, Das T, Kim M S, Ahn J H 2016 Adv. Mater. 28 4184
Google Scholar
[6] Huang C, Chen L 2016 Adv. Mater. 28 8079
Google Scholar
[7] Grima J N, Winczewski S, Mizzi L, Grech M C, Cauchi R, Gatt R, Attard D, Wojciechowski K W, Rybicki J 2015 Adv. Mater. 27 1455
Google Scholar
[8] Zhai Z R, Wu L L, Jiang H Q 2021 Appl. Phys. Rev. 8 041319
Google Scholar
[9] Yu Y, Yin Y Q, Bai R Y, Hu Y Z, Li B, Wang M Y, Chen G M 2023 Appl. Phys. Lett. 123 011702
Google Scholar
[10] Sun R J, Zhang B, Yang L, Zhang W J, Farrow I, Scarpa F, Rossiter J 2018 Appl. Phys. Lett. 112 251904
Google Scholar
[11] Han D X, Chen S H, Zhao L, Tong X, Chan K C 2022 AIP Adv. 12 035305
Google Scholar
[12] Lee J H, Singer J P, Thomas E L 2012 Adv. Mater. 24 4782
Google Scholar
[13] Grima J N, Manicaro E, Attard D 2011 Proc. R. Soc. A: Math. Phys. Eng. Sci. 467 439
Google Scholar
[14] Han T W, Scarpa F, Allan N L 2017 Thin Solid Films 632 35
Google Scholar
[15] Ho V H, Ho D T, Kwon S Y, Kim S Y 2016 Phys. Status Solidi B Basic Res. 253 1303
Google Scholar
[16] Cai K, Luo J, Ling Y R, Wan J, Qin Q H 2016 Sci. Rep. 6 35157
Google Scholar
[17] Shi P, Chen Y, Feng J, Sareh P 2024 Phys. Rev. E 109 035002
Google Scholar
[18] Shi P, Chen Y, Wei Y, Feng J, Guo T, Tu Y M, Sareh P 2023 Phys. Rev. B 108 134105
Google Scholar
[19] Wan J, Jiang J W, Park H S 2017 Nanoscale 9 4007
Google Scholar
[20] Jiang J W, Chang T C, Guo X M 2016 Nanoscale 8 15948
Google Scholar
[21] Hanakata P Z, Cubuk E D, Campbell D K, Park H S 2018 Physi. Rev. Lett. 121 255304
Google Scholar
[22] Wan J, Jiang J W, Park H S 2020 Carbon 157 262
Google Scholar
[23] Rumelhart D E, Hinton G E, Williams R J 1986 Nature 323 533
Google Scholar
[24] Slann A, White W, Scarpa F, Boba K, Farrow I 2015 Phys. Status Solidi B Basic Res. 252 1533
Google Scholar
[25] Grima J N, Mizzi L, Azzopardi K M, Gatt R 2016 Adv. Mater. 28 385
Google Scholar
[26] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, Veld P J I, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Comm. 271 10817
Google Scholar
[27] Dhaliwal G, Nair P B, Singh C V 2019 Carbon 142 300
Google Scholar
[28] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472
Google Scholar
[29] Qin H S, Sun Y, Liu J Z, Liu Y L 2016 Carbon 108 204
Google Scholar
[30] Qian C, McLean B, Hedman D, Ding F 2021 APL Mater. 9 061102
Google Scholar
[31] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[32] Hoover W G 1985 Phys. Rev. A Gen. Phys. 31 1695
Google Scholar
[33] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay É 2011 J. Mach. Learn. Res. 11 2825
Google Scholar
[34] Jones D R, Schonlau M, Welch W J 1998 J. Glob. Optim. 13 455
Google Scholar
[35] Lundberg S M, Lee S I 2017 Proceedings of the 31st Conference on Neural Information Processing Systems Long Beach, California, USA, December 4–9, 2017 pp4768–4777
-
图 1 (a) 石墨烯的原子结构; (b) 菱形穿孔代表单元; (c) 5×5菱形穿孔石墨烯剪纸模型
Fig. 1. (a) Graphene unit cell; (b) representative unit cell of graphene kirigami with labeled features; (c) perforated graphene kirigami composed of a 5 × 5 array of representative unit cells.
图 2 菱形穿孔石墨烯负泊松比预测的机器学习模型构建流程图
Fig. 2. Machine learning constructing workflow for predicting the negative Poisson’s ratio of rhombic perforated graphene.
图 4 完美无穿孔和菱形穿孔石墨烯加载过程中的纵向应变与横向应变关系曲线
Fig. 4. Longitudinal versus lateral strains during the loading of pristine and rhombic perforated graphene.
图 5 菱形穿孔石墨烯在不同应变下形貌的俯视图和侧视图, 其中虚线为未变形前模型尺寸
Fig. 5. Top and side views of rhombic perforated graphene kirigami at various tensile strains. The dashed box indicates the model dimensions prior to deformation.
图 6 BPNN训练过程和预测结果分析 (a) BPNN损失函数迭代图; (b) 预测值和真实值对比图
Fig. 6. Analysis of the BPNN training process and prediction results: (a) Iteration plot of the BPNN loss function; (b) comparison of predicted and actual values.
图 7 特征重要性分析 (a) 特征与目标变量的Pearson相关性热力图; (b) 特征重要性柱状图(基于SHAP值); (c) 特征SHAP值散点图
Fig. 7. Feature importance analysis: (a) Heatmap of Pearson correlation between features and the target variable; (b) bar chart of feature importance (based on SHAP values); (c) scatter plot of feature SHAP values.
图 8 菱形穿孔几何参数对穿孔石墨烯泊松比的影响 (a) L; (b) AR; (c) IS; (d) L固定时不同的AR和IS
Fig. 8. Influence of rhombic perforation geometric parameters on the Poisson’s ratio of perforated graphene: (a) L; (b) AR; (c) IS; (d) different AR and IS with fixed L.
表 1 调优后的BPNN参数
Table 1. Optimized BPNN parameters after adjustment.
类型 BPNN参数 输入 AR, IS, L 输出 vxy 隐藏层 91-92-27-60 激活函数 Relu 优化器 Adam 学习率 0.006701783312545704 迭代次数 1000 
下载: 导出CSV
表 2 BPNN的性能评估指标
Table 2. Performance evaluation metrics of the BPNN.
评估指标 R2 MSE MAE 训练集 0.9990 0.000326 0.01225 测试集 0.9813 0.006755 0.04633
下载: 导出CSV
-
[1] Lee C, Wei X D, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[2] Zhang Y B, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Balandin A A, Ghosh S, Bao W Z, Calizo I, Teweldebrhan D, Miao F, Lau C N 2008 Nano Lett. 8 902
Google Scholar
[5] Jang H, Park Y J, Chen X, Das T, Kim M S, Ahn J H 2016 Adv. Mater. 28 4184
Google Scholar
[6] Huang C, Chen L 2016 Adv. Mater. 28 8079
Google Scholar
[7] Grima J N, Winczewski S, Mizzi L, Grech M C, Cauchi R, Gatt R, Attard D, Wojciechowski K W, Rybicki J 2015 Adv. Mater. 27 1455
Google Scholar
[8] Zhai Z R, Wu L L, Jiang H Q 2021 Appl. Phys. Rev. 8 041319
Google Scholar
[9] Yu Y, Yin Y Q, Bai R Y, Hu Y Z, Li B, Wang M Y, Chen G M 2023 Appl. Phys. Lett. 123 011702
Google Scholar
[10] Sun R J, Zhang B, Yang L, Zhang W J, Farrow I, Scarpa F, Rossiter J 2018 Appl. Phys. Lett. 112 251904
Google Scholar
[11] Han D X, Chen S H, Zhao L, Tong X, Chan K C 2022 AIP Adv. 12 035305
Google Scholar
[12] Lee J H, Singer J P, Thomas E L 2012 Adv. Mater. 24 4782
Google Scholar
[13] Grima J N, Manicaro E, Attard D 2011 Proc. R. Soc. A: Math. Phys. Eng. Sci. 467 439
Google Scholar
[14] Han T W, Scarpa F, Allan N L 2017 Thin Solid Films 632 35
Google Scholar
[15] Ho V H, Ho D T, Kwon S Y, Kim S Y 2016 Phys. Status Solidi B Basic Res. 253 1303
Google Scholar
[16] Cai K, Luo J, Ling Y R, Wan J, Qin Q H 2016 Sci. Rep. 6 35157
Google Scholar
[17] Shi P, Chen Y, Feng J, Sareh P 2024 Phys. Rev. E 109 035002
Google Scholar
[18] Shi P, Chen Y, Wei Y, Feng J, Guo T, Tu Y M, Sareh P 2023 Phys. Rev. B 108 134105
Google Scholar
[19] Wan J, Jiang J W, Park H S 2017 Nanoscale 9 4007
Google Scholar
[20] Jiang J W, Chang T C, Guo X M 2016 Nanoscale 8 15948
Google Scholar
[21] Hanakata P Z, Cubuk E D, Campbell D K, Park H S 2018 Physi. Rev. Lett. 121 255304
Google Scholar
[22] Wan J, Jiang J W, Park H S 2020 Carbon 157 262
Google Scholar
[23] Rumelhart D E, Hinton G E, Williams R J 1986 Nature 323 533
Google Scholar
[24] Slann A, White W, Scarpa F, Boba K, Farrow I 2015 Phys. Status Solidi B Basic Res. 252 1533
Google Scholar
[25] Grima J N, Mizzi L, Azzopardi K M, Gatt R 2016 Adv. Mater. 28 385
Google Scholar
[26] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, Veld P J I, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Comm. 271 10817
Google Scholar
[27] Dhaliwal G, Nair P B, Singh C V 2019 Carbon 142 300
Google Scholar
[28] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472
Google Scholar
[29] Qin H S, Sun Y, Liu J Z, Liu Y L 2016 Carbon 108 204
Google Scholar
[30] Qian C, McLean B, Hedman D, Ding F 2021 APL Mater. 9 061102
Google Scholar
[31] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[32] Hoover W G 1985 Phys. Rev. A Gen. Phys. 31 1695
Google Scholar
[33] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay É 2011 J. Mach. Learn. Res. 11 2825
Google Scholar
[34] Jones D R, Schonlau M, Welch W J 1998 J. Glob. Optim. 13 455
Google Scholar
[35] Lundberg S M, Lee S I 2017 Proceedings of the 31st Conference on Neural Information Processing Systems Long Beach, California, USA, December 4–9, 2017 pp4768–4777
下载:
计量
- 文章访问数: 524
- PDF下载量: 26
- 被引次数: 0
