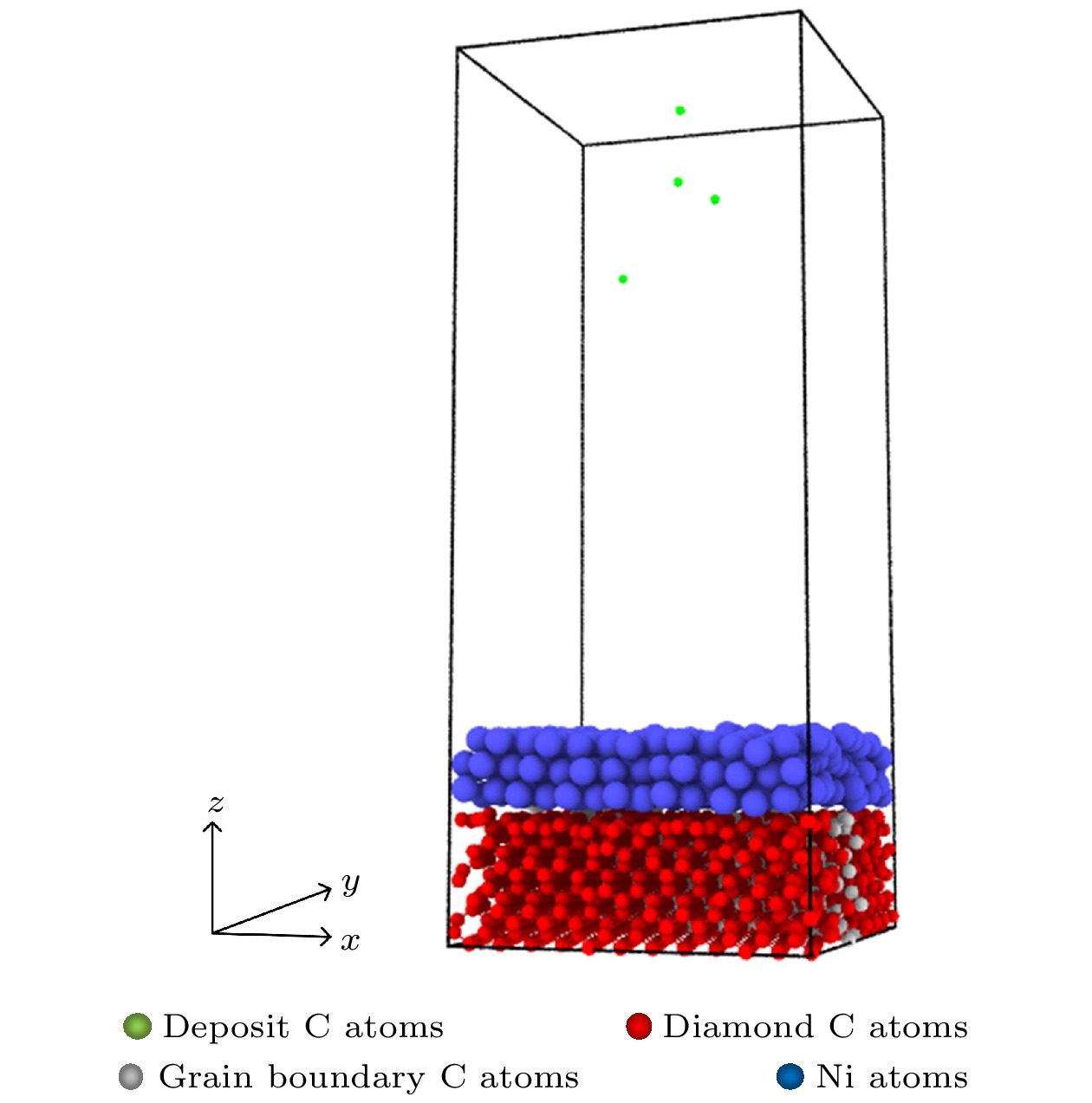
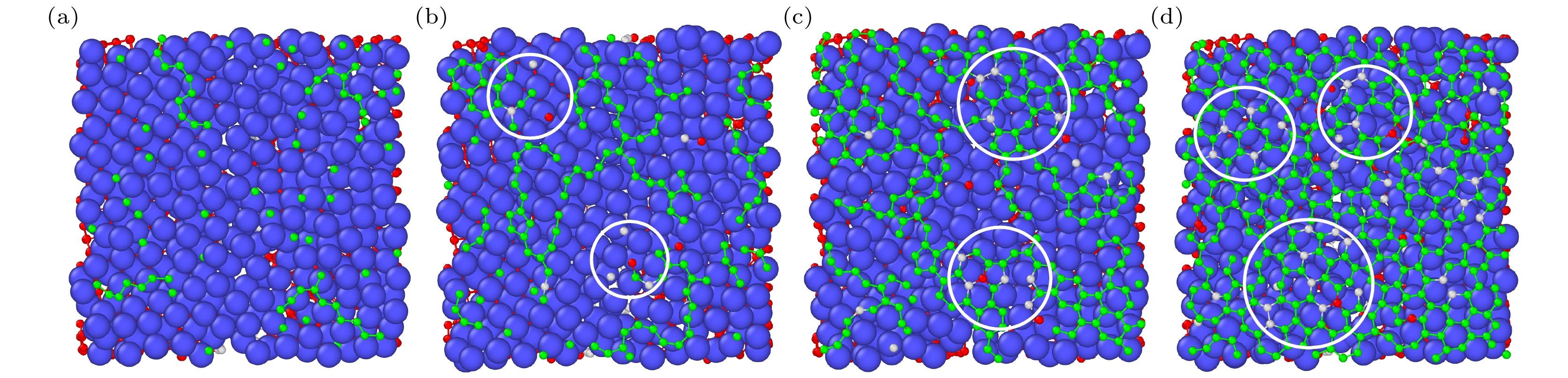
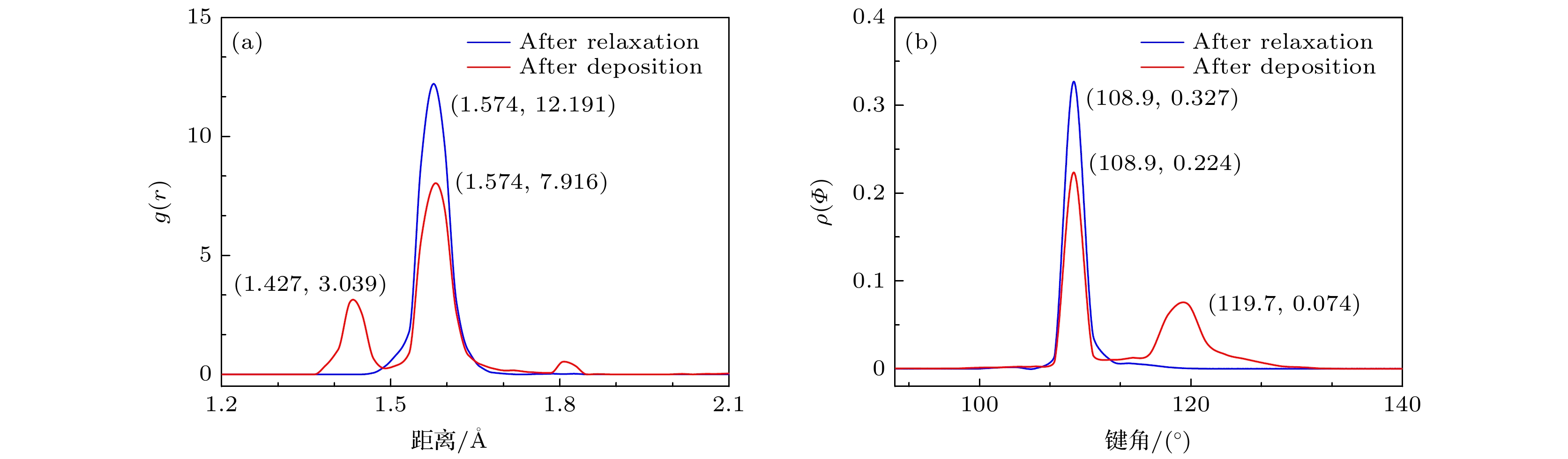
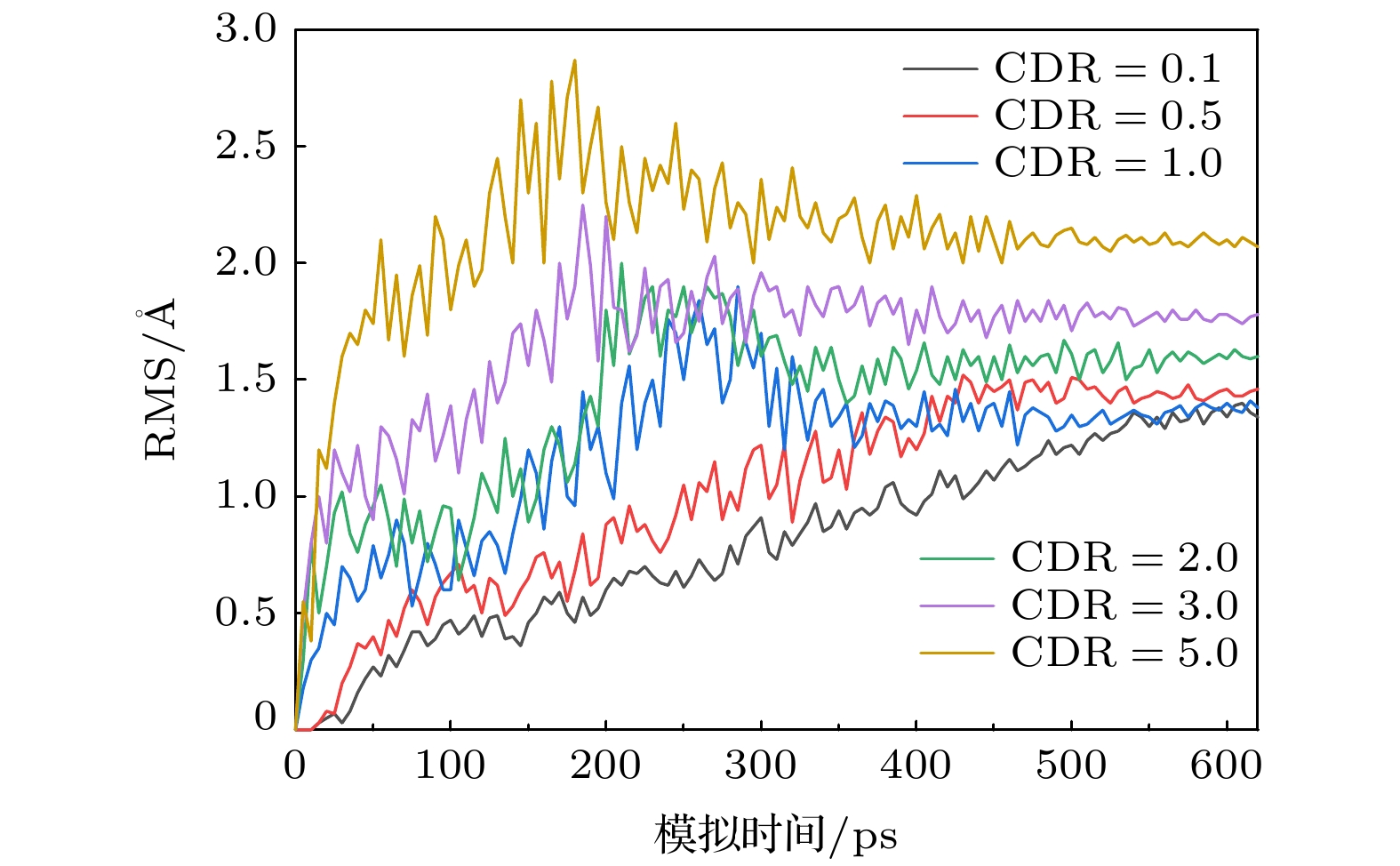
-
石墨烯在新基材上的生长一直是被关注的焦点, 而在以金刚石多晶体为基底沉积石墨烯的成核机理方面的研究对石墨烯大规模的制备具有重要的现实意义. 本文采用反应性分子动力学仿真技术, 模拟了镍催化双晶金刚石辅助石墨烯沉积生长的过程, 研究了金刚石晶界对石墨烯成核生长过程中动力学行为的影响. 研究结果表明晶界碳原子可作为补充碳源扩散至镍自由表面, 参与石墨烯的成核生长. 论文探究了温度对碳原子扩散行为的影响, 发现当沉积温度为1700 K时, 利于晶界碳原子在镍晶格中扩散, 有效提高石墨烯成核密度; 探究了沉积碳源流量对石墨烯表面质量影响, 发现1700 K下采用较低的碳沉积速率1 ps–1有利于获得最佳的石墨烯表面质量. 本文的研究结果不仅为金刚石晶界辅助石墨烯沉积生长提供了有效的理论模型和机理解析, 还揭示了沉积温度和沉积碳源流量对生长石墨烯表面质量的影响规律, 为石墨烯/金刚石多晶体异质结构在超精密制造和微电子领域的实际应用提供理论基础.The growth of high-quality graphene is always a focused issue in the field of two-dimensional materials, and the growth of graphene on brand new substrates has received considerable attention from scholars especially. The research on the nucleation mechanism of graphene deposited on a polycrystalline diamond substrate is of significance in the large-scale preparation of graphene in practice. Here in this work, the direct growth without transfer process of graphene on a diamond substrate is used to obtain the high-quality graphene. The reactive molecular dynamics simulation technology is adopted to imitate the process of graphene deposition and growth on bi-crystal diamond assisted by nickel catalyzed at an atomic level. The effect of the bi-crystal diamond grain boundary on the dynamic behavior of graphene nucleation and growth process is studied. The results demonstrate that the grain boundary carbon atoms can be used as a supplementary carbon source to diffuse into the nickel free surface and participate in the nucleation and growth of graphene. Furthermore, the effect of temperature on the diffusion behavior of carbon atoms is explored, finding that high temperature facilitates the dissociation of atoms in the grain boundary. When the deposition temperature equals 1700 K, it is most conducive to the diffusion of grain boundary carbon atoms in the nickel lattice, which effectively enhances the nucleation density of graphene. Besides, the effect of the deposition carbon source flow rate on the surface quality of graphene is explored, finding that the high-quality graphene surface can be obtained by adopting a lower carbon deposit rate of 1 ps–1 at 1700 K. In brief, the research results obtained not only provide an effective theoretical model and analysis of the mechanism for diamond grain boundary assisted graphene deposition and growth, but also reveal the regular pattern of influence of deposition temperature and deposition carbon source flow rate on the surface quality of synthesized graphene. The present study can lay a theoretical foundation for the fabrication and application of new functional graphene-polycrystalline diamond heterostructures in the fields of ultra-precision manufacturing and microelectronics.
-
Keywords:
- graphene /
- diamond grain boundary /
- deposition and growth /
- molecular dynamics
[1] He X, Bai Q, Shen R 2018 Carbon 130 672
Google Scholar
[2] Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[3] Zhu L, Wang J, Zhang T, Ma L, Lim C W, Ding F, Zeng X C 2010 Nano Lett. 10 494
Google Scholar
[4] Paolicelli G, Tripathi M, Corradini V, Candini A, Valeri S 2015 Nanotechnology 26 055703
Google Scholar
[5] Peng Y, Zeng X, Liu L, Cao X, Zou K, Chen R 2017 Carbon 124 541
Google Scholar
[6] Egberts P, Han G H, Liu X Z, Johnson A T C, Carpick R W 2014 ACS Nano 8 5010
Google Scholar
[7] Freitag M 2010 Phys. Status Solidi B 247 2895
Google Scholar
[8] He L, Wang J, Hou K, Yang S 2019 Appl. Surf. Sci. 475 389
Google Scholar
[9] Lui C H, Liu L, Mak K F, Flynn G W, Heinz T F 2009 Nature 462 339
Google Scholar
[10] Zapol P, Sternberg M, Curtiss L A, Frauenheim T, Gruen D M 2002 Phys. Rev. B 65 045403
Google Scholar
[11] Ueda K, Aichi S, Asano H 2016 Diam. Relat. Mater. 63 148
Google Scholar
[12] Berman D, Deshmukh S A, Narayanan B, Sankaranarayanan S K R S, Yan Z, Balandin A A, Zinovev A, Rosenmann D, Sumant A V 2016 Nat. Commun. 7 12099
Google Scholar
[13] Kanada S, Nagai M, Ito S, Matsumoto T, Ogura M, Takeuchi D, Yamasaki S, Inokuma T, Tokuda N 2017 Diam. Relat. Mater. 75 105
Google Scholar
[14] Barnard A S, Sternberg M 2008 J. Comput. Theor. Nanosci. 5 2089
Google Scholar
[15] Tokuda N, Makino T, Inokuma T, Yamsaki S, Inokuma T 2012 Jpn. J. Appl. Phys. 51 090107
Google Scholar
[16] Rasuli R, Mostafavi K, Davoodi J 2014 J. Appl. Phys. 115 185503
Google Scholar
[17] Syuhada I, Rosikhin A, Fikri A, Noor F A, Winata T 2016 API Conf. Proc. 1710 185503
Google Scholar
[18] Xu Z, Yan T, Liu G, Qiao G, Ding F 2015 Nanoscale 8 921
Google Scholar
[19] 王浪, 冯伟, 杨连乔, 张建华 2014 63 176801
Google Scholar
Wang L, Feng W, Yang L Q, Zhang J H 2014 Acta Phys. Sin. 63 176801
Google Scholar
[20] Mueller J E, Van Duin A C T, Dasgupta S, Lorant F, Goddard W A 2001 J. Phys. Chem. A 105 9396
Google Scholar
[21] L Meng, Q Sun, J Wang, F Ding 2012 J. Phys. Chem. C 116 6097
Google Scholar
[22] Neyts E C, Van Duin A C T, Bogaerts A 2013 Nanoscale 5 7250
Google Scholar
[23] Mueller J E, Van Duin A C T, Goddard W A 2010 J. Phys. Chem. C 114 4939
Google Scholar
[24] Neyts E C, Van Duin A C T, Bogaerts A 2011 J. Am. Chem. Soc. 133 17225
Google Scholar
[25] Neyts E C, Shibuta Y, van Duin A C T, Bogaerts A 2010 ACS Nano 4 6665
Google Scholar
[26] Van Duin A C T, Strachan A, Stewman S, Zhang Q S, Xu X, Goddard W A 2003 J. Phys. Chem. A 107 3803
Google Scholar
[27] Tao C G, Feng H J, Zhou J, Lue L H, Lu X H 2009 Acta Phys-Chim. Sin. 25 1373
Google Scholar
[28] Gao J, Yuan Q, Hu H, Zhao J, Ding F 2011 J. Phys. Chem. C 115 16795
Google Scholar
[29] Wang L, Zhang X, Chan H L W, Yan F, Ding F 2013 J. AM. Chem. Soc. 135 4476
Google Scholar
[30] Reina A, Jia X, Ho J, Neizich D, Son H, Bulovic V, Dresselhaus M S, Kong J 2008 Nano Lett. 9 30
Google Scholar
[31] Page A J, Ohta Y, Okamoto Y, Irle S, Morokuma K 2009 J. Phys. Chem. C 113 20198
Google Scholar
-
图 1 双晶金刚石基底仿真模型 (a)俯视图; (b)正视图
Fig. 1. Simulation model of bi-crystal diamond substrate: (a) Top view; (b) front view.
图 2 金刚石晶界辅助石墨烯沉积仿真模型
Fig. 2. Simulation model of graphene deposition assisted by grain boundary.
图 3 1700 K下镍催化双晶金刚石辅助石墨烯沉积生长过程的顶面原子分布 (a) 80 ps; (b) 170 ps; (c) 270 ps; (d) 380 ps
Fig. 3. Top atomic distribution of graphene deposition and growth on bi-crystal diamond assisted by nickel catalyzed at 1700 K: (a) 80 ps; (b) 170 ps; (c) 270 ps; (d) 380 ps.
图 4 1700 K下镍催化双晶金刚石辅助石墨烯沉积生长过程的侧面原子分布 (a) 80 ps; (b) 170 ps; (c) 270 ps; (d) 380 ps
Fig. 4. Lateral atomic distribution of graphene deposition and growth on bi-crystal diamond assisted by nickel catalyzed at 1700 K: (a) 80 ps; (b) 170 ps; (c) 270 ps; (d) 380 ps.
图 5 沉积前后模拟体系的 (a)径向分布函数, (b)价键角分布函数
Fig. 5. (a) RDF and (b) ADF of initial and final deposition simulation system.
图 6 不同温度下晶界及金刚石顶部晶面裂解的 (a) 碳原子数和(b)扩散系数
Fig. 6. (a) The number of carbon atom and (b) diffusion coefficient of grain boundary and top of diamond at various temperatures.
图 7 不同碳沉积速率下石墨烯的顶面生长情况 (a) 0.5 ps–1; (b) 1.0 ps–1; (c) 2.0 ps–1; (d) 3.0 ps–1; (e) 5.0 ps–1
Fig. 7. Top growth of graphene at various CDR: (a) 0.5 ps–1; (b) 1.0 ps–1; (c) 2.0 ps–1; (d) 3.0 ps–1; (e) 5.0 ps–1.
图 8 不同碳沉积速率下石墨烯的侧面生长情况 (a) 0.5 ps–1; (b) 1.0 ps–1; (c) 2.0 ps–1; (d) 3.0 ps–1; (e) 5.0 ps–1
Fig. 8. Lateral growth of graphene at various CDR: (a) 0.5 ps–1; (b) 1.0 ps–1; (c) 2.0 ps–1; (d) 3.0 ps–1; (e) 5.0 ps–1.
图 9 不同碳沉积速率生长石墨烯的RMS变化情况
Fig. 9. The change of graphene RMS with time at different CDR.
-
[1] He X, Bai Q, Shen R 2018 Carbon 130 672
Google Scholar
[2] Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385
Google Scholar
[3] Zhu L, Wang J, Zhang T, Ma L, Lim C W, Ding F, Zeng X C 2010 Nano Lett. 10 494
Google Scholar
[4] Paolicelli G, Tripathi M, Corradini V, Candini A, Valeri S 2015 Nanotechnology 26 055703
Google Scholar
[5] Peng Y, Zeng X, Liu L, Cao X, Zou K, Chen R 2017 Carbon 124 541
Google Scholar
[6] Egberts P, Han G H, Liu X Z, Johnson A T C, Carpick R W 2014 ACS Nano 8 5010
Google Scholar
[7] Freitag M 2010 Phys. Status Solidi B 247 2895
Google Scholar
[8] He L, Wang J, Hou K, Yang S 2019 Appl. Surf. Sci. 475 389
Google Scholar
[9] Lui C H, Liu L, Mak K F, Flynn G W, Heinz T F 2009 Nature 462 339
Google Scholar
[10] Zapol P, Sternberg M, Curtiss L A, Frauenheim T, Gruen D M 2002 Phys. Rev. B 65 045403
Google Scholar
[11] Ueda K, Aichi S, Asano H 2016 Diam. Relat. Mater. 63 148
Google Scholar
[12] Berman D, Deshmukh S A, Narayanan B, Sankaranarayanan S K R S, Yan Z, Balandin A A, Zinovev A, Rosenmann D, Sumant A V 2016 Nat. Commun. 7 12099
Google Scholar
[13] Kanada S, Nagai M, Ito S, Matsumoto T, Ogura M, Takeuchi D, Yamasaki S, Inokuma T, Tokuda N 2017 Diam. Relat. Mater. 75 105
Google Scholar
[14] Barnard A S, Sternberg M 2008 J. Comput. Theor. Nanosci. 5 2089
Google Scholar
[15] Tokuda N, Makino T, Inokuma T, Yamsaki S, Inokuma T 2012 Jpn. J. Appl. Phys. 51 090107
Google Scholar
[16] Rasuli R, Mostafavi K, Davoodi J 2014 J. Appl. Phys. 115 185503
Google Scholar
[17] Syuhada I, Rosikhin A, Fikri A, Noor F A, Winata T 2016 API Conf. Proc. 1710 185503
Google Scholar
[18] Xu Z, Yan T, Liu G, Qiao G, Ding F 2015 Nanoscale 8 921
Google Scholar
[19] 王浪, 冯伟, 杨连乔, 张建华 2014 63 176801
Google Scholar
Wang L, Feng W, Yang L Q, Zhang J H 2014 Acta Phys. Sin. 63 176801
Google Scholar
[20] Mueller J E, Van Duin A C T, Dasgupta S, Lorant F, Goddard W A 2001 J. Phys. Chem. A 105 9396
Google Scholar
[21] L Meng, Q Sun, J Wang, F Ding 2012 J. Phys. Chem. C 116 6097
Google Scholar
[22] Neyts E C, Van Duin A C T, Bogaerts A 2013 Nanoscale 5 7250
Google Scholar
[23] Mueller J E, Van Duin A C T, Goddard W A 2010 J. Phys. Chem. C 114 4939
Google Scholar
[24] Neyts E C, Van Duin A C T, Bogaerts A 2011 J. Am. Chem. Soc. 133 17225
Google Scholar
[25] Neyts E C, Shibuta Y, van Duin A C T, Bogaerts A 2010 ACS Nano 4 6665
Google Scholar
[26] Van Duin A C T, Strachan A, Stewman S, Zhang Q S, Xu X, Goddard W A 2003 J. Phys. Chem. A 107 3803
Google Scholar
[27] Tao C G, Feng H J, Zhou J, Lue L H, Lu X H 2009 Acta Phys-Chim. Sin. 25 1373
Google Scholar
[28] Gao J, Yuan Q, Hu H, Zhao J, Ding F 2011 J. Phys. Chem. C 115 16795
Google Scholar
[29] Wang L, Zhang X, Chan H L W, Yan F, Ding F 2013 J. AM. Chem. Soc. 135 4476
Google Scholar
[30] Reina A, Jia X, Ho J, Neizich D, Son H, Bulovic V, Dresselhaus M S, Kong J 2008 Nano Lett. 9 30
Google Scholar
[31] Page A J, Ohta Y, Okamoto Y, Irle S, Morokuma K 2009 J. Phys. Chem. C 113 20198
Google Scholar
下载:
计量
- 文章访问数: 4854
- PDF下载量: 95
- 被引次数: 0
