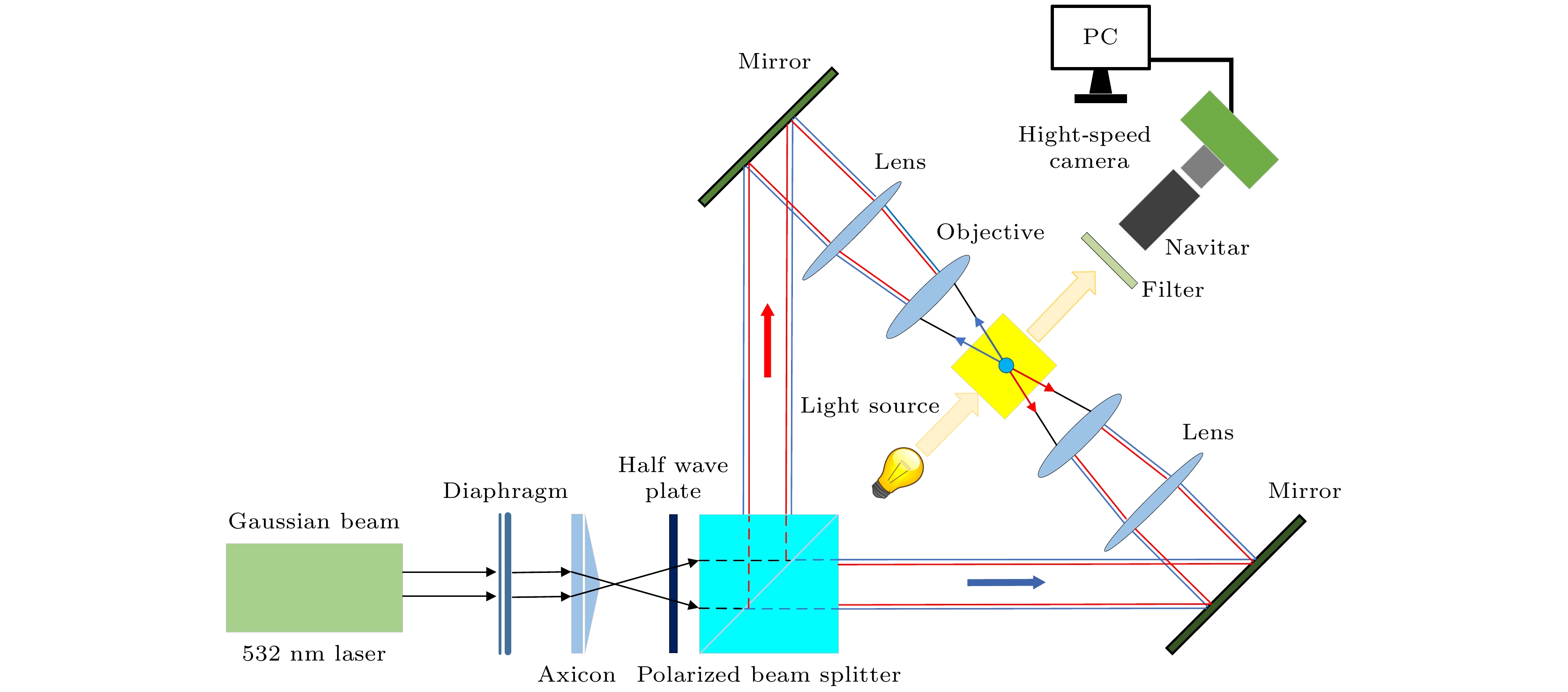
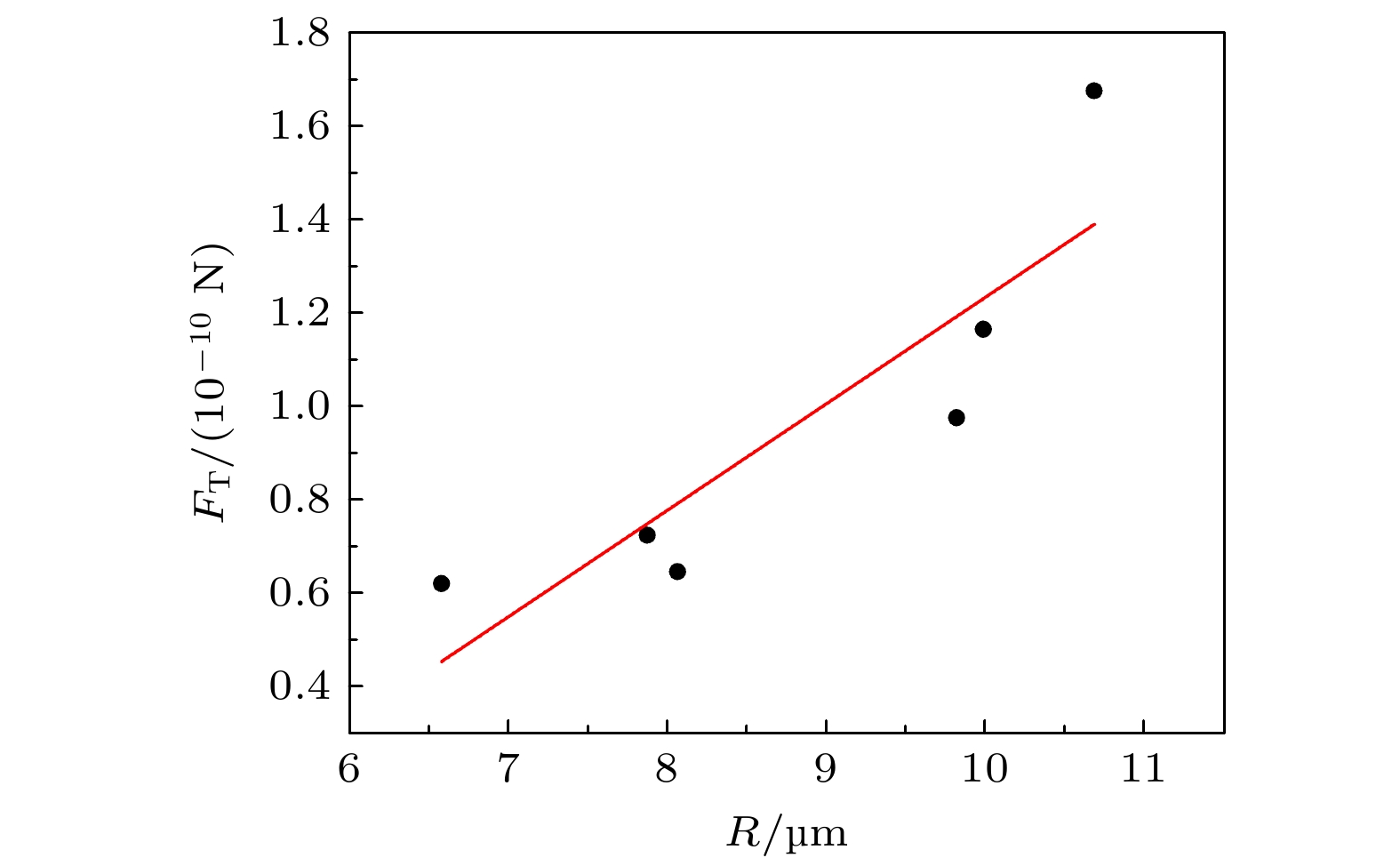
-
为了探索空气中强吸收纳米粒子团簇在激光作用下的悬浮以及迁移行为, 提出采用反向传输的双贝塞尔光束对纳米粒子团簇进行捕获及悬浮, 而后释放团簇, 观察和计算分析团簇的迁移行为. 两束贝塞尔光束由锥透镜和偏振分光方式产生, 进行反向水平布置, 形成三维光阱, 光阱刚度可通过调节两束贝塞尔光束的功率比进行控制. 悬浮室内的粒子通过微弱气流进行流化, 而后被光阱捕获和悬浮. 采用高速摄像仪对团簇的悬浮及迁移过程进行记录, 然后通过图像分析来获取粒子运动参数. 以强吸收性超细煤粉粒子团簇为对象, 首先对其进行悬浮和释放迁移的实验研究, 而后对团簇所受的光泳力、重力、浮力、曳力以及热泳力进行计算和分析. 实验和计算的结果表明: 强吸收性纳米粒子团簇在激光作用下产生的光泳力占主导作用; 团簇能够被稳定地悬浮在反向传输的双贝塞尔光束形成的三维势阱中, 通过调整悬浮的位置而达到与重力、浮力、曳力等的动态平衡; 利用悬浮的相对不稳定度分析评价强吸收性粒子团簇的稳定性, 超细煤粉粒子团簇的最小相对不稳定度可达0.075; 通过对团簇释放后的高速图像进行分析, 可获得团簇的迁移运动参数, 从而测量出团簇所受的热泳力; 对于等效粒径为13—21 μm的超细煤粉粒子团簇, 其热泳力量级为10–11—10–10 N, 随着团簇粒径的增大, 热泳力线性增大, 与理论计算结果趋势一致. 通过利用激光对粒子进行悬浮和释放的方式为热泳力的测量和研究提供了一种新的研究思路, 也为气体介质中粒子的控制和输运展现了一种新的操控手段.In order to explore the levitation and migration behavior of strongly absorbing nanoparticle clusters in air by using laser technique, in this study trapping and levitating nanoparticle clusters is proposed based on the counter-propagated bi-Bessel beams, and then the clusters are released to observe and analyze their migration behaviors. Two Bessel beams are generated by a conical lens and polarizing beam splitter, arranged horizontally in reverse to form a three-dimensional optical trap. The stiffness of the optical trap can be controlled by adjusting the power ratio of the two Bessel beams. The particles in the levitation chamber are fluidized through weak airflow, and then captured and levitated by a light trap. A high-speed camera is used to record the levitation and migration process of clusters. The particle motion parameters can be obtained through image analysis. The strong-absorbing ultrafine coal particle clusters are first selected to conduct the experiments on their levitation and release migration. Then, the photophorestic force, gravity, buoyancy, drag force, and thermophorestic force acting on the clusters are calculated and analyzed. The experimental and computational results indicate that the photophorestic force of air-borne strong-absorbing nanoparticle clusters generated by laser illumination dominates the levitation; nanoparticle clusters can be stably levitated in a three-dimensional potential well formed by counter-propagated bi-Bessel beams, achieving dynamic equilibrium with gravity, buoyancy, drag, etc. by adjusting the levitation position. The relative instability parameter of levitation is used to evaluate the stability of air-borne strong-absorbing nanoparticle clusters, and the minimum relative instability of ultrafine coal particle clusters reaches 0.075. By analyzing the images of nanoparticle cluster recorded by high-speed camera after being released, the migration motion parameters of the cluster can be obtained, therefore the thermophorestic force acting on the cluster is accurately measured. For the ultrafine coal particle clusters with equivalent particle sizes in a range of approximately 13–21 μm, the magnitudes of their thermophorestic forces are in a range of 10–11–10–10 N. As the cluster size increases, the thermophorestic force increases linearly, which is consistent with the theoretical calculation trend. The use of laser to levitate and release particles provides a novel approach for measuring and analyzing thermophorestic force, and also presents a novel manipulation tool for controlling and transporting particles in a gaseous medium.
-
Keywords:
- laser levitation /
- photophorestic force /
- thermophoretic force /
- strong-absorbing nanoparticle clusters
[1] Ashkin A, Dziedzic J 1975 Science 187 1073
Google Scholar
[2] 黄雪峰, 李盛姬, 周东辉, 赵冠军, 王关晴, 徐江荣 2014 63 178802
Google Scholar
Huang X F, Li S J, Zhou D H, Zhao G J, Wang G Q, Xu J R 2014 Acta Phys. Sin. 63 178802
Google Scholar
[3] Huisken J, Stelzer E H K 2002 Opt. Lett. 27 1223
Google Scholar
[4] Meresman H, Wills J B, Summers M, McGloin D, Reid J P 2009 Phys. Chem. Chem. Phys. 11 11333
Google Scholar
[5] Zhang Z, Cannan D, Liu J J, Zhang P, Christodoulides D N, Chen Z G 2012 Opt. Express 20 16212
Google Scholar
[6] Pan Y L, Hill S C, Coleman M 2012 Opt. Express 20 5325
Google Scholar
[7] Rings D, Schachoff R, Selmke M, Cichos F, Kroy K 2010 Phys. Rev. Lett. 105 090604
Google Scholar
[8] Gong Z Y, Pan Y L, Wang C J 2016 Rev. Sci. Instrum. 87 156
Google Scholar
[9] Keh H J, Tu H J 2001 Colloids Surfaces A 176 213
Google Scholar
[10] Malaia N V, Shchukin E R 2019 Tech. Phys. 64 458
Google Scholar
[11] Chang Y C, Keh H J 2012 Journal of Aerosol Science 50 1
Google Scholar
[12] Maxwell J C 1879 Phil. Trans. R. Soc. 170 231
Google Scholar
[13] Kennard E H 1938 Kinetic Theory of Gases (New York: McGraw-Hill) p291
[14] Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101 [崔杰, 苏俊杰, 王军, 夏国栋, 李志刚 2021 70 055101]
Google Scholar
Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101
Google Scholar
[15] Greene W M, Spjut R E, Bar-Ziv E, Sarofim A F, Longwell J P 1985 J. Opt. Soc. Am. B 2 998
Google Scholar
[16] Chernyah V, Beresnev S 1993 J. Aerosol Sci. 24 857
Google Scholar
[17] Mackowski D W 1989 Int. J. Heat Mass Transf. 32 843
Google Scholar
[18] Frueh J, Rutkowski S, Si T, Ren Y X, Gai M, Tverdokhlebov S I, Qiu G, Schmitt J, He Q, Wang J 2021 Appl. Surf. Sci. 549 149319
Google Scholar
[19] Burelbach J, Zupkauskas M, Lamboll R, Lan Y, Eiser E 2017 J. Chem. Phys. 147 094906
Google Scholar
[20] Li L, Loyalka S K, Tamadate T, Sapkota D, Ouyang H, Hogan Jr C J 2024 J. Aerosol Sci. 178 106337
Google Scholar
[21] Li W, Davis E J 1995 J. Aerosol Sci. 26 1063
Google Scholar
[22] Zheng F, Davis E J 2001 Aerosol Sci. 32 1421
Google Scholar
[23] Bosworth R W, Ventura A L, Ketsdever A D, Gimelshein S F 2016 J. Fluid Mech. 805 207
Google Scholar
[24] 黄雪峰, 陈矗, 李嘉欣, 张敏琦, 李盛姬 2023 72 174201
Google Scholar
Huang X F, Chen C, Li J X, Zhang M Q, Li S J 2023 Acta Phys. Sin. 72 174201
Google Scholar
[25] Dusel P W, Kerker M, Cooke D D 1979 J. Opt. Sot. Am. 69 55
Google Scholar
[26] Pluchino A B 1983 Appl. Opt. 22 103
Google Scholar
[27] Yalamov Y I, Kutukov V B, Shchukin E R 1976 J. Colioid Interface Sci. 57 564
Google Scholar
[28] McPeak K M, Jayanti S V, Kress S J, Meyer S, Iotti S, Rossinelli A, Norris D J 2015 ACS Photonics 2 326
Google Scholar
[29] Wang H Y, Wang J J, Dong W Q, Han Y P, Ambrosio L A, Liu L 2021 Opt. Express 29 26894
Google Scholar
[30] Epstein P S 1929 Z. Phys. 54 537
Google Scholar
-
图 1 (a) 超细煤粉颗粒的扫描电子显微镜图片; (b) 超细煤粉团簇的图片
Fig. 1. (a) Scanning electron microscope picture of a super fine pulverized coal particle; (b) picture of pulverized coal cluster.
图 4 (a) 被稳定悬浮的团簇照片; (b) 不同时刻的悬浮团簇图像; (c) 悬浮团簇的等效粒径及波动位移
Fig. 4. (a) Photo of a stably suspended coal cluster; (b) images of the suspended cluster at different moments; (c) equivalent particle size and fluctuating displacement of the suspended cluster.
图 5 (a) 团簇迁移运动过程图像; (b) 位移矢量图; (c) 热泳力矢量图; (d) 热泳力、曳力和有效重力的变化情况对比
Fig. 5. (a) Images during cluster migration movement; (b) displacement vector diagram; (c) thermophorestic force vector diagram; (d) comparison of the thermophorestic force, drag force, and effective gravity.
图 6 不同粒径团簇的位移矢量图与相应的热泳力、曳力和有效重力的变化情况 (a), (b)团簇1; (c), (d) 团簇2; (e), (f) 团簇3; (g), (h) 团簇4; (i), (j) 团簇5; (k), (l) 团簇6
Fig. 6. Comparison of displacement vector and the corresponding thermophorestic force, drag force, and effective gravity: (a), (b) Cluster 1; (c), (d) cluster 2; (e), (f) cluster 3; (g), (h) cluster 4; (i), (j) cluster 5; (k), (l) cluster 6.
图 7 热泳力随强吸收性团簇半径的变化
Fig. 7. Variation of thermophorestic force with the radius of strong-absorbing clusters.
图 8 不对称因子随粒径参数(a)和贝塞尔光束半锥角(b)的变化
Fig. 8. Variation of asymmetry factor J1 with particle size parameter (a) and half-cone angle (b).
图 9 微粒在不均匀温度场中的热泳力形成示意图 (a) 不均匀温度场; (b) 气体分子与微粒的碰撞
Fig. 9. Schematic of thermophorestic force formation of microparticle in non-uniform temperature field: (a) Non-uniform temperature field; (b) collision between gas molecules and microparticle.
图 10 以光阱中心为原点在竖直方向上气体温度变化及拟合曲线
Fig. 10. Gas temperature variation and fitting curve in the vertical direction with the center of the optical trap as the origin.
图 11 热泳力随团簇尺寸参数(a)和温度梯度(b)的变化
Fig. 11. Variation of thermophoretic force with cluster size parameter (a) and temperature gradient (b).
-
[1] Ashkin A, Dziedzic J 1975 Science 187 1073
Google Scholar
[2] 黄雪峰, 李盛姬, 周东辉, 赵冠军, 王关晴, 徐江荣 2014 63 178802
Google Scholar
Huang X F, Li S J, Zhou D H, Zhao G J, Wang G Q, Xu J R 2014 Acta Phys. Sin. 63 178802
Google Scholar
[3] Huisken J, Stelzer E H K 2002 Opt. Lett. 27 1223
Google Scholar
[4] Meresman H, Wills J B, Summers M, McGloin D, Reid J P 2009 Phys. Chem. Chem. Phys. 11 11333
Google Scholar
[5] Zhang Z, Cannan D, Liu J J, Zhang P, Christodoulides D N, Chen Z G 2012 Opt. Express 20 16212
Google Scholar
[6] Pan Y L, Hill S C, Coleman M 2012 Opt. Express 20 5325
Google Scholar
[7] Rings D, Schachoff R, Selmke M, Cichos F, Kroy K 2010 Phys. Rev. Lett. 105 090604
Google Scholar
[8] Gong Z Y, Pan Y L, Wang C J 2016 Rev. Sci. Instrum. 87 156
Google Scholar
[9] Keh H J, Tu H J 2001 Colloids Surfaces A 176 213
Google Scholar
[10] Malaia N V, Shchukin E R 2019 Tech. Phys. 64 458
Google Scholar
[11] Chang Y C, Keh H J 2012 Journal of Aerosol Science 50 1
Google Scholar
[12] Maxwell J C 1879 Phil. Trans. R. Soc. 170 231
Google Scholar
[13] Kennard E H 1938 Kinetic Theory of Gases (New York: McGraw-Hill) p291
[14] Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101 [崔杰, 苏俊杰, 王军, 夏国栋, 李志刚 2021 70 055101]
Google Scholar
Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101
Google Scholar
[15] Greene W M, Spjut R E, Bar-Ziv E, Sarofim A F, Longwell J P 1985 J. Opt. Soc. Am. B 2 998
Google Scholar
[16] Chernyah V, Beresnev S 1993 J. Aerosol Sci. 24 857
Google Scholar
[17] Mackowski D W 1989 Int. J. Heat Mass Transf. 32 843
Google Scholar
[18] Frueh J, Rutkowski S, Si T, Ren Y X, Gai M, Tverdokhlebov S I, Qiu G, Schmitt J, He Q, Wang J 2021 Appl. Surf. Sci. 549 149319
Google Scholar
[19] Burelbach J, Zupkauskas M, Lamboll R, Lan Y, Eiser E 2017 J. Chem. Phys. 147 094906
Google Scholar
[20] Li L, Loyalka S K, Tamadate T, Sapkota D, Ouyang H, Hogan Jr C J 2024 J. Aerosol Sci. 178 106337
Google Scholar
[21] Li W, Davis E J 1995 J. Aerosol Sci. 26 1063
Google Scholar
[22] Zheng F, Davis E J 2001 Aerosol Sci. 32 1421
Google Scholar
[23] Bosworth R W, Ventura A L, Ketsdever A D, Gimelshein S F 2016 J. Fluid Mech. 805 207
Google Scholar
[24] 黄雪峰, 陈矗, 李嘉欣, 张敏琦, 李盛姬 2023 72 174201
Google Scholar
Huang X F, Chen C, Li J X, Zhang M Q, Li S J 2023 Acta Phys. Sin. 72 174201
Google Scholar
[25] Dusel P W, Kerker M, Cooke D D 1979 J. Opt. Sot. Am. 69 55
Google Scholar
[26] Pluchino A B 1983 Appl. Opt. 22 103
Google Scholar
[27] Yalamov Y I, Kutukov V B, Shchukin E R 1976 J. Colioid Interface Sci. 57 564
Google Scholar
[28] McPeak K M, Jayanti S V, Kress S J, Meyer S, Iotti S, Rossinelli A, Norris D J 2015 ACS Photonics 2 326
Google Scholar
[29] Wang H Y, Wang J J, Dong W Q, Han Y P, Ambrosio L A, Liu L 2021 Opt. Express 29 26894
Google Scholar
[30] Epstein P S 1929 Z. Phys. 54 537
Google Scholar
下载:
计量
- 文章访问数: 1419
- PDF下载量: 68
- 被引次数: 0
