-
近年来, 实验技术和理论计算在实现超快时间尺度的分辨以及对于原子尺度微观细节的解析上都有了突破性进展, 对于水体系的超快微观动力学也带来了更多新的认识. 本文将视角集中于水分子、水团簇以及液态水在不同强度的光激发下产生的电离、解离甚至等离子体化的过程, 总结了人们在前沿工作中获得的有关水体系原子尺度超快动力学的知识. 特别地, 围绕光电离实验探讨了阿秒尺度的电离延迟以及水分子Feshbach共振理论分析; 围绕液态水的解离过程探讨了水合电子产生、空穴的定域化等重要过程, 补足了液态水解离完整过程的微观图像; 围绕水的等离子体化介绍了通过含时密度泛函等方法计算得到的水在强激光脉冲作用下转变为等离子体状态的过程与机制, 总结了在极高电子温度下水的特殊电子结构的相关知识. 这些讨论将给出当前人们看待水的激发态的相对全面的视角.
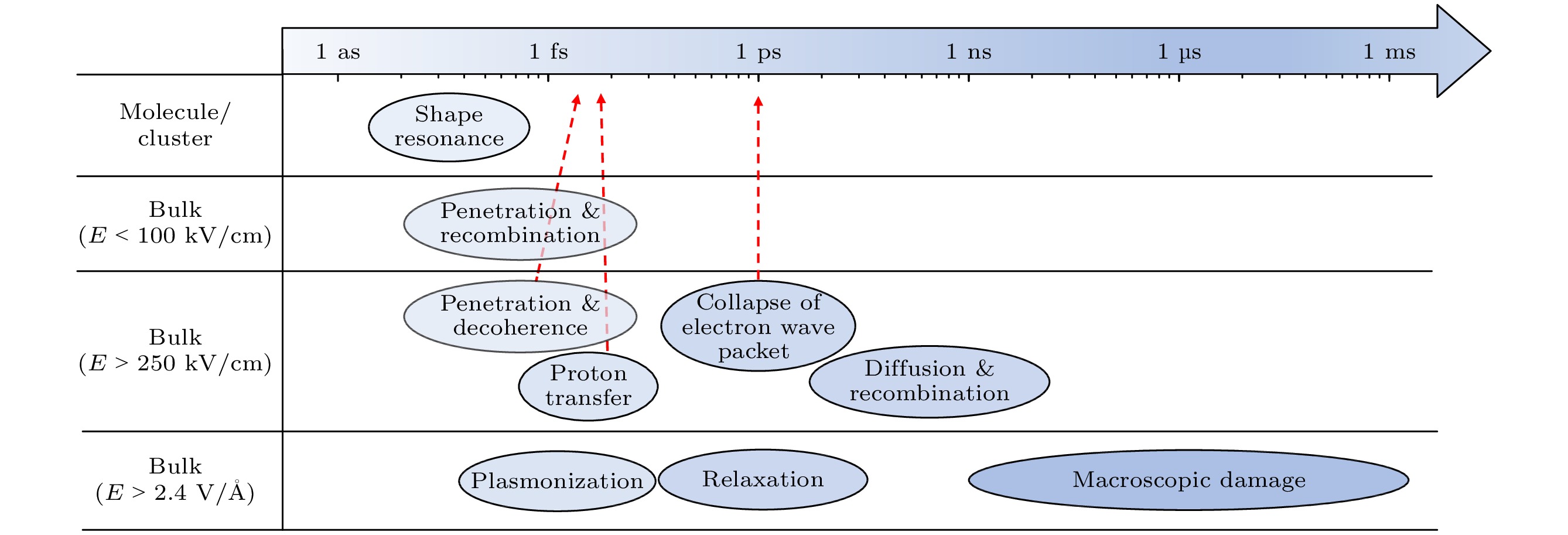
Experimental techniques and theoretical calculations have made significant breakthroughs recently in realizing the ultrafast time resolution and the understanding of microscopic details on an atomic scale, which has brought new insights into the ultrafast microscopic dynamics of water system and aqueous system. Here we focus on the dynamic processes of ionization, dissociation, as well as plasmonization of water molecules, water clusters, and liquid water under different intensities of light excitation. The pump-probe technique allows one to extract the information about the orbital-dependent phase shift during photoionization, corresponding to delays on a time scale from tens to hundreds of attoseconds. Delay time in photoionization is found to be proportional to the delocalization of molecular/cluster orbitals. In addition, the information related to the Feshbach resonance is also of interest. By solving the scattering equations, the detailed information about the scattering cross section, the β-parameter, and the involved Rydberg orbitals during valence electron ionization of water is obtained. For liquid water undergoing irradiation by an optical field, the tunneling electrons are unable to move away and recombine with the parent molecule on a time scale of 100 fs if the external field is not strong enough (e.g. ~100 kV/cm). For terahertz fields as high as 250 kV/cm, electrons will move away from the parent molecule after tunnelling and undergo decoherence on a 10-fs time scale. At the beginning of tunneling the electrons will be more delocalized and will collapse to a certain position on a time scale of ~1 ps, and then slowly diffuse or recombine with holes on a longer time scale. For the strong excitation case, hot electrons may also be formed. When a hot electron is located on a particular water molecule, the O—H bond will be broken. When an electron ionizes away, a hole will be created. The hole will be located on a water molecule within 10 fs, and will trigger off subsequent processes such as proton transfer and coherent oscillations. In particular, after the hole is localized and before the proton is transferred, there is a brief appearance of the metastable $ {{{\mathrm{H}}}_{2}{\mathrm{O}}}^{+} $ ion, whose lifetime is experimentally captured and is predicted to be (46±10) fs. The nuclear quantum effect in this process plays a key role.Using the methods such as real time-time dependent density functional theory (rt-TDDFT), it is found that the water undergoes plasmonization under intense laser pulses corresponding to a field strength amplitude larger than 2.4 V/Å. The effective electron temperature in this period reaches over 20000 K. Strongly excited water in this state exhibits the behaviors of a liquid metal, and extremely strong nonthermal effect and nonadiabatic effect. In the process of plasmonization, a large fraction of chemical bonds in water molecules are broken and reorganize themselves, and many chemical species such as hydrogen molecules may appear, which also implies that laser-induced plasmonization can be used to synthesize new substances. Although the previous researches have brought about a very rich understanding, we have also found some details that still need to be explored: i) the influence of nuclear quantum effects has not been taken into account in most of theoretical calculations, which may result in the inadequate description and inaccurate prediction; ii) some of the microscopic details observed in simulations do not yet have a direct counterpart in experimental measurements; iii) the current simulation of water plasmonization is for the local behavior under the spatially uniform external field, while in the real situation there are spatial inhomogeneity and energy flow, which urgently need larger-scale excited state dynamics simulations. With the development of laser technology, the integration of water science and ultrafast technologies will be increasingly strong, so we believe that such a systematic understanding will play a key role in the future. It is expected that new research efforts will continue to contribute to a better understanding and the generation of new technologies in this exciting research field. -
Keywords:
- photoexcitation /
- water /
- ultrafast dynamics /
- excited state
[1] van Dishoeck E F, Herbst E, Neufeld D A 2013 Chem. Rev. 113 9043
 Google Scholar
Google Scholar
[2] Zhong J, Kumar M, Anglada J M, Martins-Costa M T C, Ruiz-Lopez M F, Zeng X C, Francisco J S 2019 Annu. Rev. Phys. Chem. 70 45
 Google Scholar
Google Scholar
[3] Bhattacharyya K 2008 Chem. Commun. 25 2848
 Google Scholar
Google Scholar
[4] Laage D, Elsaesser T, Hynes J T 2017 Chem. Rev. 117 10694
 Google Scholar
Google Scholar
[5] Ma R, Cao D, Zhu C, Tian Y, Peng J, Guo J, Chen J, Li X Z, Francisco J S, Zeng X C, Xu L M, Wang E G, Jiang Y 2020 Nature 577 60
 Google Scholar
Google Scholar
[6] Huang X, Wang L, Liu K, Liao L, Sun H, Wang J, Tian X, Xu Z, Wang W, Liu L, Jiang Y, Chen J, Wang E, Bai X 2023 Nature 617 86
 Google Scholar
Google Scholar
[7] Debenedetti P G, Sciortino F, Zerze G H 2020 Science 369 289
 Google Scholar
Google Scholar
[8] Wagstaffe M, Dominguez-Castro A, Wenthaus L, Palutke S, Kutnyakhov D, Heber M, Pressacco F, Dziarzhytski S, Gleissner H, Gupta V K, Redlin H, Dominguez A, Frauenheim T, Rubio A, Stierle A, Noei H 2023 Phys. Rev. Lett. 130 108001
 Google Scholar
Google Scholar
[9] Sudera P, Cyran J D, Deiseroth M, Backus E H G, Bonn M 2020 J. Am. Chem. Soc. 142 12005
 Google Scholar
Google Scholar
[10] Flanagan J C, Valentine M L, Baiz C R 2020 Acc. Chem. Res. 53 1860
 Google Scholar
Google Scholar
[11] Hummer G, Rasaiah J C, Noworyta J P 2001 Nature 414 188
 Google Scholar
Google Scholar
[12] Gallagher K R, Sharp K A 2003 J. Am. Chem. Soc. 125 9853
 Google Scholar
Google Scholar
[13] Tielrooij K J, Garcia-Araez N, Bonn M, Bakker H J 2010 Science 328 1006
 Google Scholar
Google Scholar
[14] Hribar B, Southall N T, Vlachy V, Dill K A 2002 J. Am. Chem. Soc. 124 12302
 Google Scholar
Google Scholar
[15] Gong X, Heck S, Jelovina D, Perry C, Zinchenko K, Lucchese R, Worner H J 2022 Nature 609 507
 Google Scholar
Google Scholar
[16] Huppert M, Jordan I, Baykusheva D, von Conta A, Worner H J 2016 Phys. Rev. Lett. 117 093001
 Google Scholar
Google Scholar
[17] Herbert J M, Coons M P 2017 Annu. Rev. Phys. Chem. 68 447
 Google Scholar
Google Scholar
[18] Savolainen J, Uhlig F, Ahmed S, Hamm P, Jungwirth P 2014 Nat. Chem. 6 697
 Google Scholar
Google Scholar
[19] Ghalgaoui A, Koll L M, Schutte B, Fingerhut B P, Reimann K, Woerner M, Elsaesser T 2020 J. Phys. Chem. Lett. 11 7717
 Google Scholar
Google Scholar
[20] Zhang Z, Piatkowski L, Bakker H J, Bonn M 2011 J. Chem. Phys. 135 021101
 Google Scholar
Google Scholar
[21] Sudera P, Cyran J D, Bonn M, Backus E H G 2021 J. Phys. Chem. C 125 22937
 Google Scholar
Google Scholar
[22] Venkatraman R K, Baiz C R 2020 Langmuir 36 6502
 Google Scholar
Google Scholar
[23] Chen Z, Na X, Curry C B, Liang S, French M, Descamps A, DePonte D P, Koralek J D, Kim J B, Lebovitz S, Nakatsutsumi M, Ofori-Okai B K, Redmer R, Roedel C, Schörner M, Skruszewicz S, Sperling P, Toleikis S, Mo M Z, Glenzer S H 2021 Matter Radiat. Extremes 6 054401
 Google Scholar
Google Scholar
[24] Lu L, Wildman A, Jenkins A J, Young L, Clark A E, Li X 2020 J. Phys. Chem. Lett. 11 9946
 Google Scholar
Google Scholar
[25] Lan J, Kapil V, Gasparotto P, Ceriotti M, Iannuzzi M, Rybkin V V 2021 Nat. Commun. 12 766
 Google Scholar
Google Scholar
[26] Xu J, Chen D, Meng S 2021 J. Am. Chem. Soc. 143 10382
 Google Scholar
Google Scholar
[27] Seideman T 2002 Annu. Rev. Phys. Chem. 53 41
 Google Scholar
Google Scholar
[28] Pazourek R, Nagele S, Burgdörfer J 2015 Rev. Mod. Phys. 87 765
 Google Scholar
Google Scholar
[29] Committee P S 1986 Atomic, Molecular, and Optical Physics: Panel on Atomic, Molecular, and Optical Physics (Washington, D. C. : National academy press
[30] Schoun S B, Chirla R, Wheeler J, Roedig C, Agostini P, DiMauro L F, Schafer K J, Gaarde M B 2014 Phys. Rev. Lett. 112 153001
 Google Scholar
Google Scholar
[31] Borras V J, Gonzalez-Vazquez J, Argenti L, Martin F 2021 J. Chem. Theory Comput. 17 6330
 Google Scholar
Google Scholar
[32] Fernandez-Milan P, Borras V J, Gonzalez-Vazquez J, Martin F 2023 J. Chem. Phys. 158 134305
 Google Scholar
Google Scholar
[33] Alizadeh E, Orlando T M, Sanche L 2015 Annu. Rev. Phys. Chem. 66 379
 Google Scholar
Google Scholar
[34] Wilhelm J, VandeVondele J, Rybkin V V 2019 Angew. Chem. Int. Ed. 58 3890
 Google Scholar
Google Scholar
[35] Pizzochero M, Ambrosio F, Pasquarello A 2019 Chem. Sci. 10 7442
 Google Scholar
Google Scholar
[36] Loh Z H, Doumy G, Arnold C, Kjellsson L, Southworth S, Al Haddad A, Kumagai Y, Tu M F, Ho P, March A 2020 Science 367 179
 Google Scholar
Google Scholar
[37] Shepard C, Kanai Y 2022 Phys. Chem. Chem. Phys. 24 5598
 Google Scholar
Google Scholar
[38] Marsalek O, Elles C G, Pieniazek P A, Pluharova E, VandeVondele J, Bradforth S E, Jungwirth P 2011 J. Chem. Phys. 135 224510
 Google Scholar
Google Scholar
[39] Zhao R, You P, Meng S 2023 Phys. Rev. Lett. 130 166401
 Google Scholar
Google Scholar
[40] Jones L O, Schatz G C 2023 J. Phys. Chem. Lett. 14 3521
 Google Scholar
Google Scholar
[41] Schaffer C B, Nishimura N, Glezer E N, Kim A M-T, Mazur E 2002 Opt. Express 10 196
 Google Scholar
Google Scholar
[42] Klein A L, Bouwhuis W, Visser C W, Lhuissier H, Sun C, Snoeijer J H, Villermaux E, Lohse D, Gelderblom H 2015 Phys. Rev. Appl. 3 044018
 Google Scholar
Google Scholar
[43] Stan C A, Milathianaki D, Laksmono H, Sierra R G, McQueen Trevor A, Messerschmidt M, Williams G J, Koglin J E, Lane T J, Hayes Matt J, Guillet S A H, Liang M, Aquila A L, Willmott P R, Robinson Joseph S, Gumerlock K L, Botha S, Nass K, Schlichting I, Shoeman Robert L, Stone H A, Boutet S 2016 Nat. Phys. 12 966
 Google Scholar
Google Scholar
[44] Beyerlein K R, Jönsson H O, Alonso-Mori R, Aquila A, Bajt S, Barty A, Bean R, Koglin J E, Messerschmidt M, Ragazzon D 2018 Proc. Natl. Acad. Sci. U. S. A. 115 5652
 Google Scholar
Google Scholar
[45] Medvedev N, Voronkov R, Volkov A E 2023 J. Chem. Phys. 158 074501
 Google Scholar
Google Scholar
-
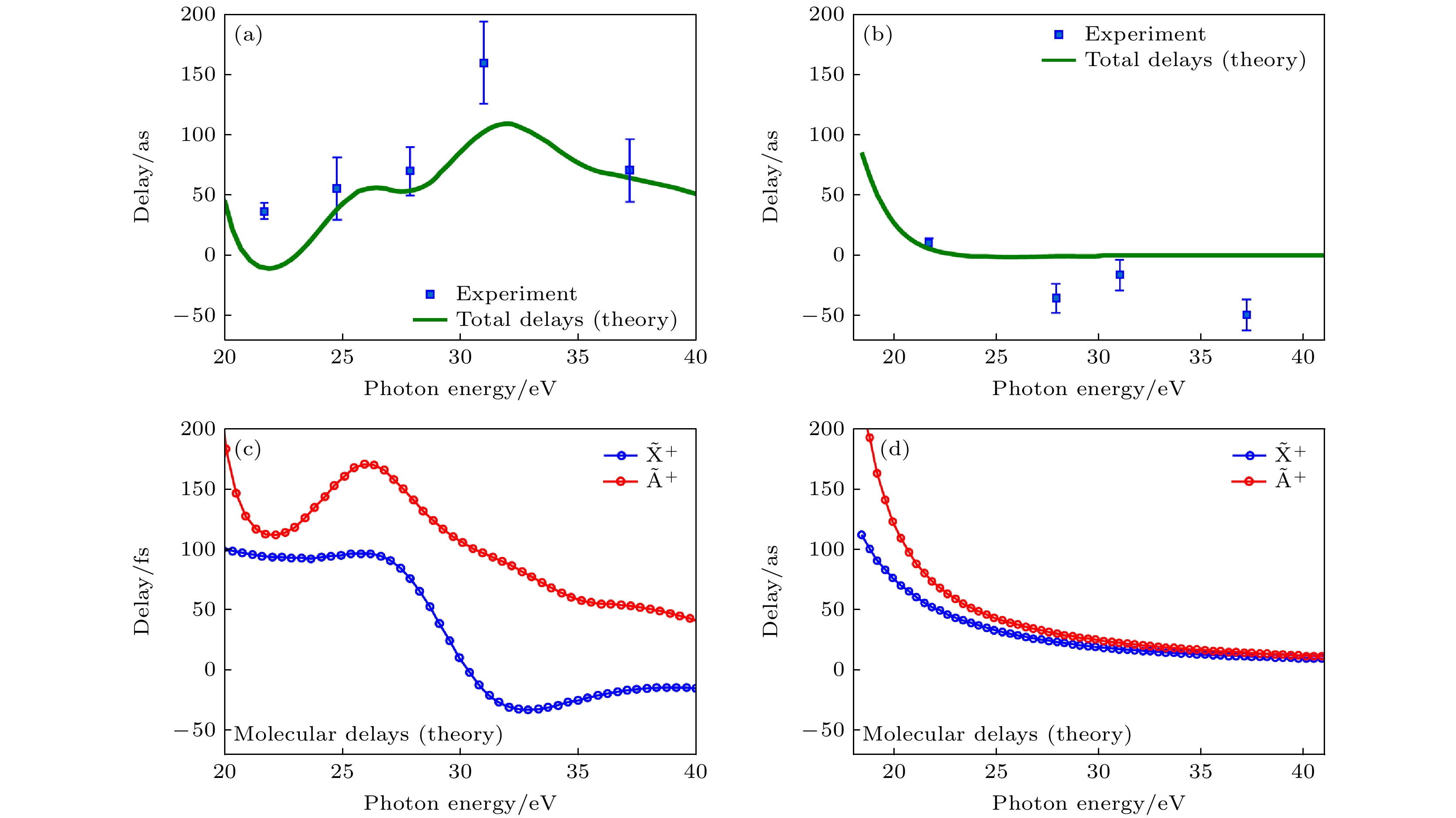
图 2 (a) 计算和测量得到的光电子从N2O+的$ {\widetilde{{\mathrm{A}}}}^{+} $和$ {\widetilde{{\mathrm{X}}}}^{+} $态离开的时间延迟[16]; (b) 与图(a)相同, 针对H2O分子[16]; (c), (d) 对于两个物种计算得到的分子延迟[16]
Fig. 2. (a) Measured and calculated delays between photo electrons leaving N2O+ in its $ {\widetilde{{\mathrm{A}}}}^{+} $ or $ {\widetilde{{\mathrm{X}}}}^{+} $ states[16], (b) same as Figure (a) for H2O[16]; (c), (d) calculated molecular delays for the two species[16].
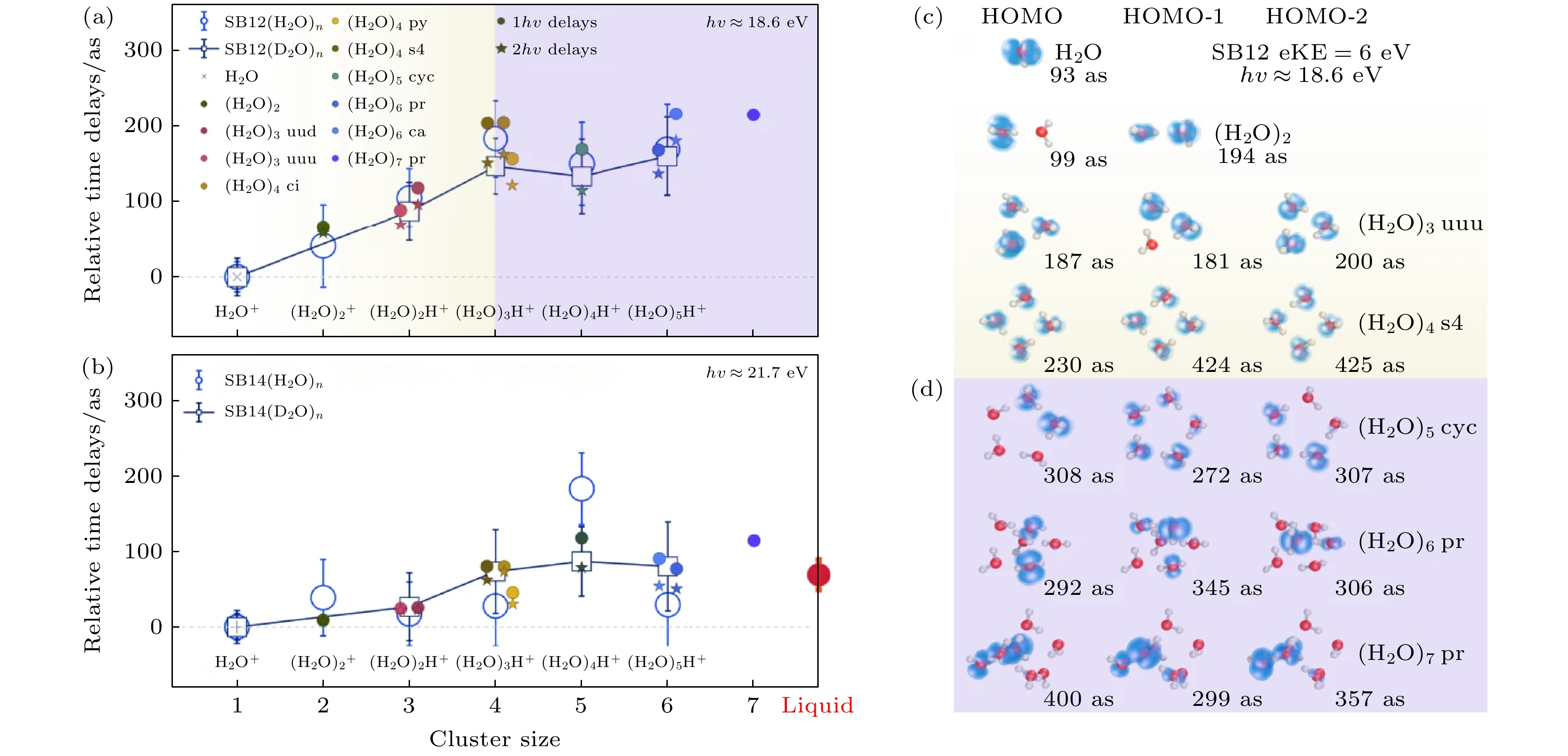
图 3 水团簇的尺寸分辨光电离时间延迟 (a) 相对于H2O (或 D2O), 在SB12中测得的水团簇1b1分波的光电离时间延迟(空心圆圈). 误差条代表95%的置信区间. 计算的延迟(实心符号)是在6.0 eV的动能下得到的[15]. (b) 与图(a)相同, 但对应于边带SB14, 其中计算值是在9.1 eV的动能下得到的. 单光子(1hν)和双光子(2hν)延迟计算结果分别以实心圆圈和星形表示[15]. (c), (d) 不同尺寸水团簇1b1轨道1—3 HOMO (记作HOMO-i)的电子密度图和计算的绝对光电离延迟. 在图(c)中以黄色背景表示了电子基本在整个团簇上离域, 而图(d)中紫色背景表示只定域在部分水分子上的情况[15]
Fig. 3. Size-resolved photoionization time delays of water clusters. (a) Time delays for photoionization out of the 1b1 band of water clusters, relative to H2O (or D2O), measured in SB12 (empty circles). The error bars represent 95% confidence intervals. The calculated delays (filled symbols) were obtained for a kinetic energy of 6.0 eV[15]. (b) Same as Figure (a), but measured for SB14, or calculated with kinetic energy (eKE) of 9.1 eV, the one-photon (1hν) and two-photon (2hν) delay calculations are presented as filled circles and stars, respectively[15]. (c), (d) Electron density map and calculated absolute photoionization delays of the 1–3 HOMO of the 1b1 band of water clusters (designated HOMO-i), highlighting the effect of delocalization (yellow shading), followed by partial localization (Figure (d), violet shading)[15].
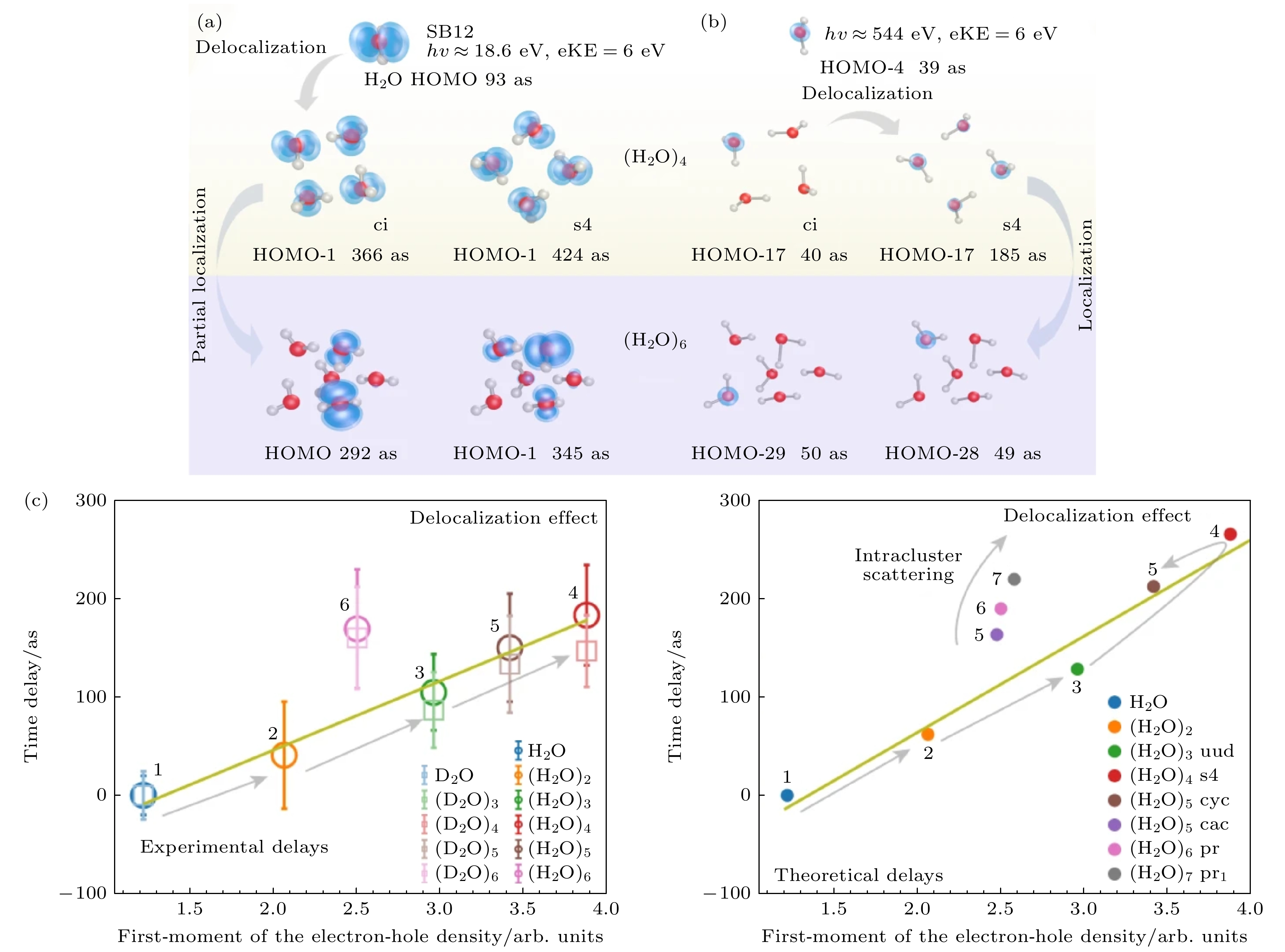
图 4 轨道离域性对水团簇光电离延迟的影响 (a) 动能(eKE)为6.0 eV时对应水团簇1b1轨道的光电离延迟, 与SB12中的实验测量结果一致[15]; (b) 与图(a)相同, 对水簇的O-1s波段使用相同的动能但是调整了光子能量[15]; (c) 光离子化时间延迟与对应水团簇1b1带的电子-空穴密度的一阶矩之间的相关性. 误差条代表 95% 的置信区间[15]
Fig. 4. Effect of orbital delocalization on photoionization delays of water clusters: (a) Photoionization delays for the 1b1 band of water clusters for a kinetic energy of eKE = 6.0 eV, corresponding to the experimental measurements in SB12[15]; (b) same as Figure (a), but for the O-1s band of water clusters using the same kinetic energy, and a correspondingly adjusted photon energy[15]; (c) correlation between the photoionization time delays and the first moment of the electron-hole density of the 1b1 band of water clusters (eKE = 6.0 eV). The error bars represent 95% confidence intervals[15].
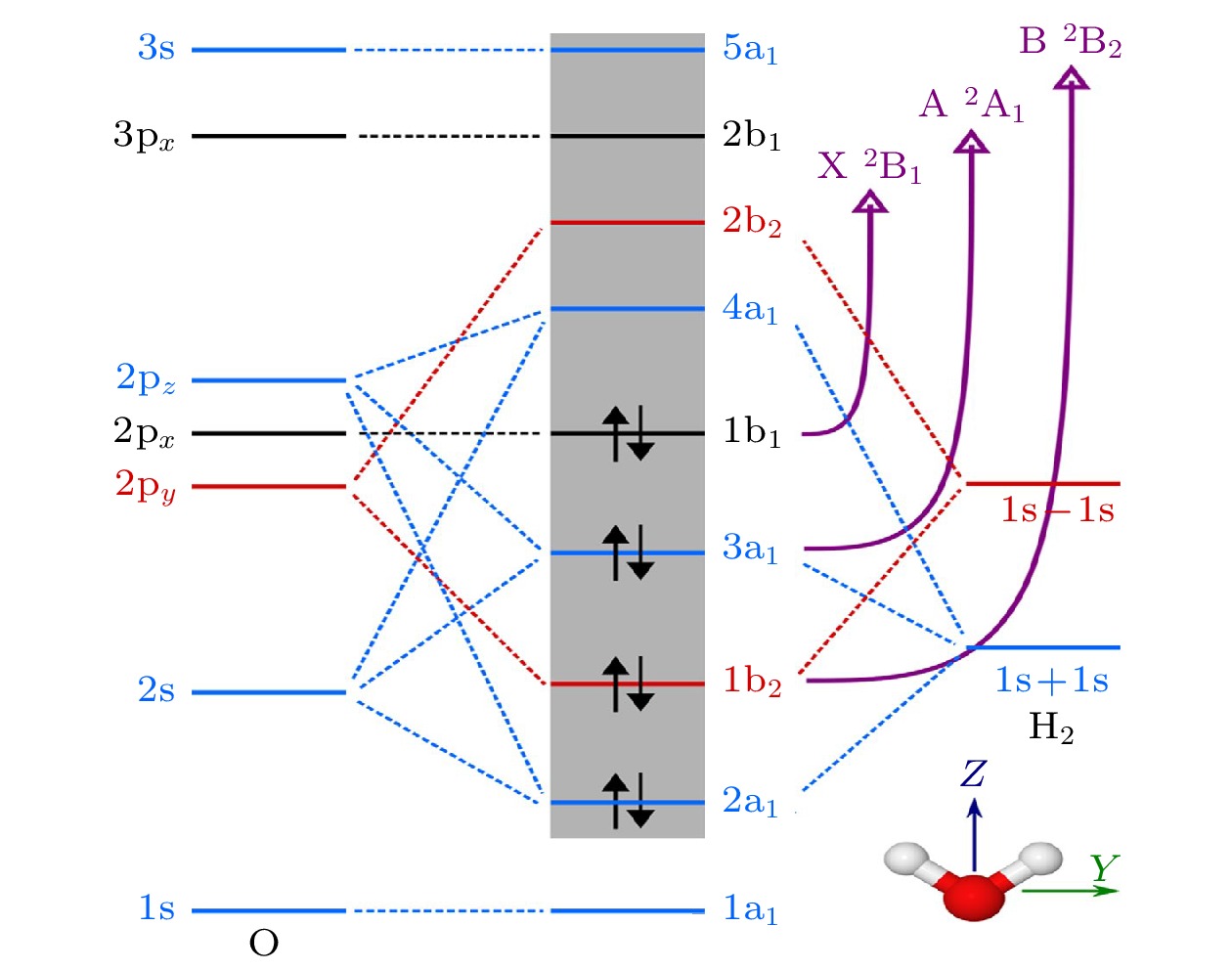
图 5 H2O的分子轨道示意图以及移除相应电子产生的阳离子态$ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1} $, $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $和$ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $. 不同的轨道对称性以不同的颜色显示: (蓝色) a1, (红色) b1 和(黑色) b2. 灰色背景包含活性空间中的轨道. 插图还显示了水分子的方向, 其中z轴与C2旋转轴重合[32]
Fig. 5. Schematic molecular orbital diagram of H2O and the corresponding electron removals that give rise to the cation states $ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1} $, $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $, and $ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $. Different orbital symmetries appear with different colors: (blue) a1, (red) b1, and (black) b2. The gray background contains the orbitals included in the active space. The orientation of the water molecule is also shown, with the z axis coinciding with the C2 rotation axis[32].
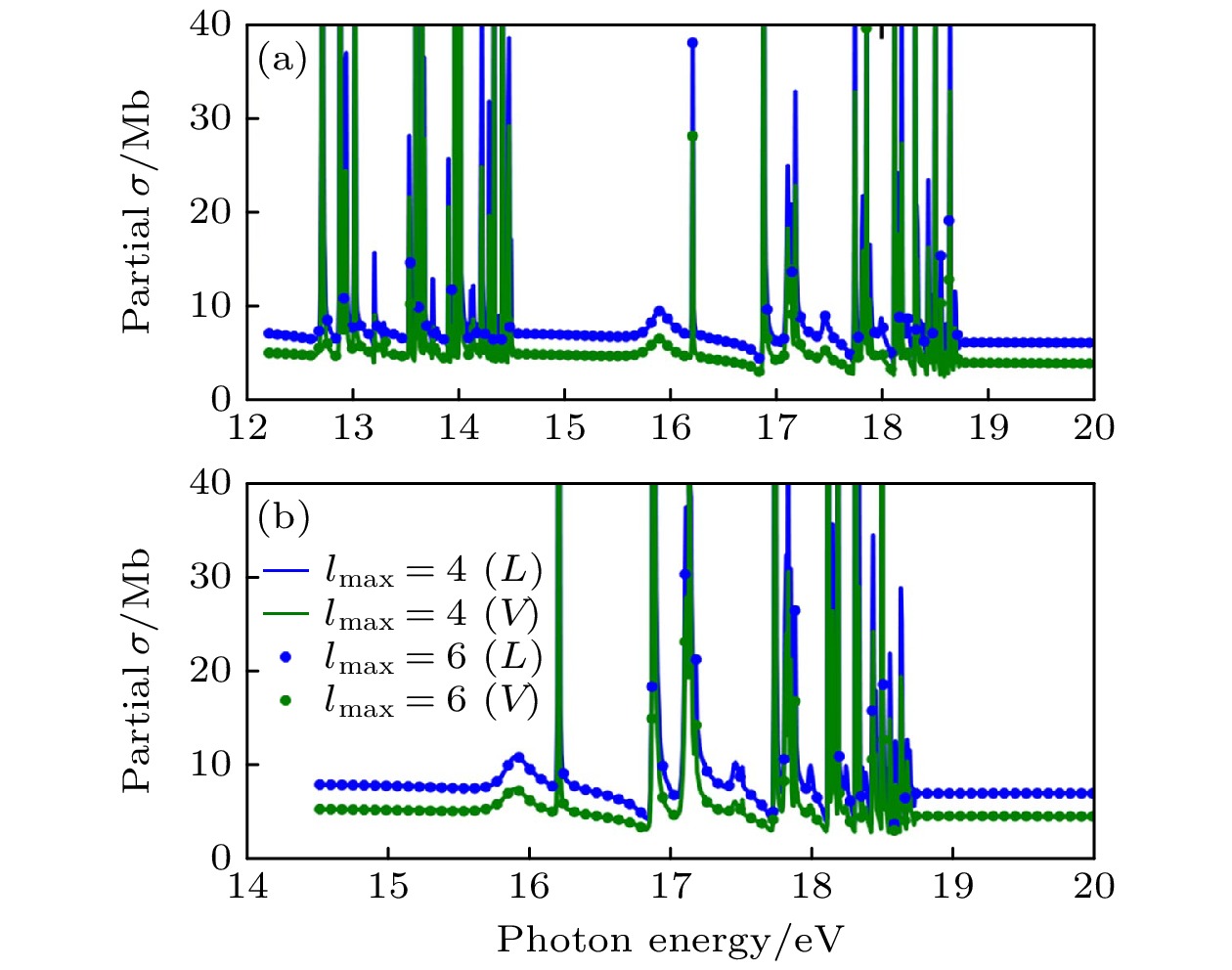
图 6 在两组不同角动量截断下用XCHEM计算获得的H2O单光子电离的方向平均部分截面. 计算考虑了12至19 eV之间的能量区域 (a) 离开$ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1} $态离子的部分电离截面[32]; (b) 离开$ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $态离子的部分电离截面. 蓝色和绿色分别对应长度规范(L)和速度规范(V). 实线和点线分别对应最大角量子数$ {l}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $为4和6 [32]
Fig. 6. Orientation-averaged partial cross sections for single-photon ionization of H2O obtained from two XCHEM calculations with different angular momentum bases in the energy region between 12 and 19 eV: (a) Partial ionization cross section for leaving the ion in the $ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1} $ state[32]; (b) same for the $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $ state. Blue: length gauge. Green: velocity gauge. Solid line: $ {l}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}= 4 $. Dots: $ {l}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}= 6 $[32].
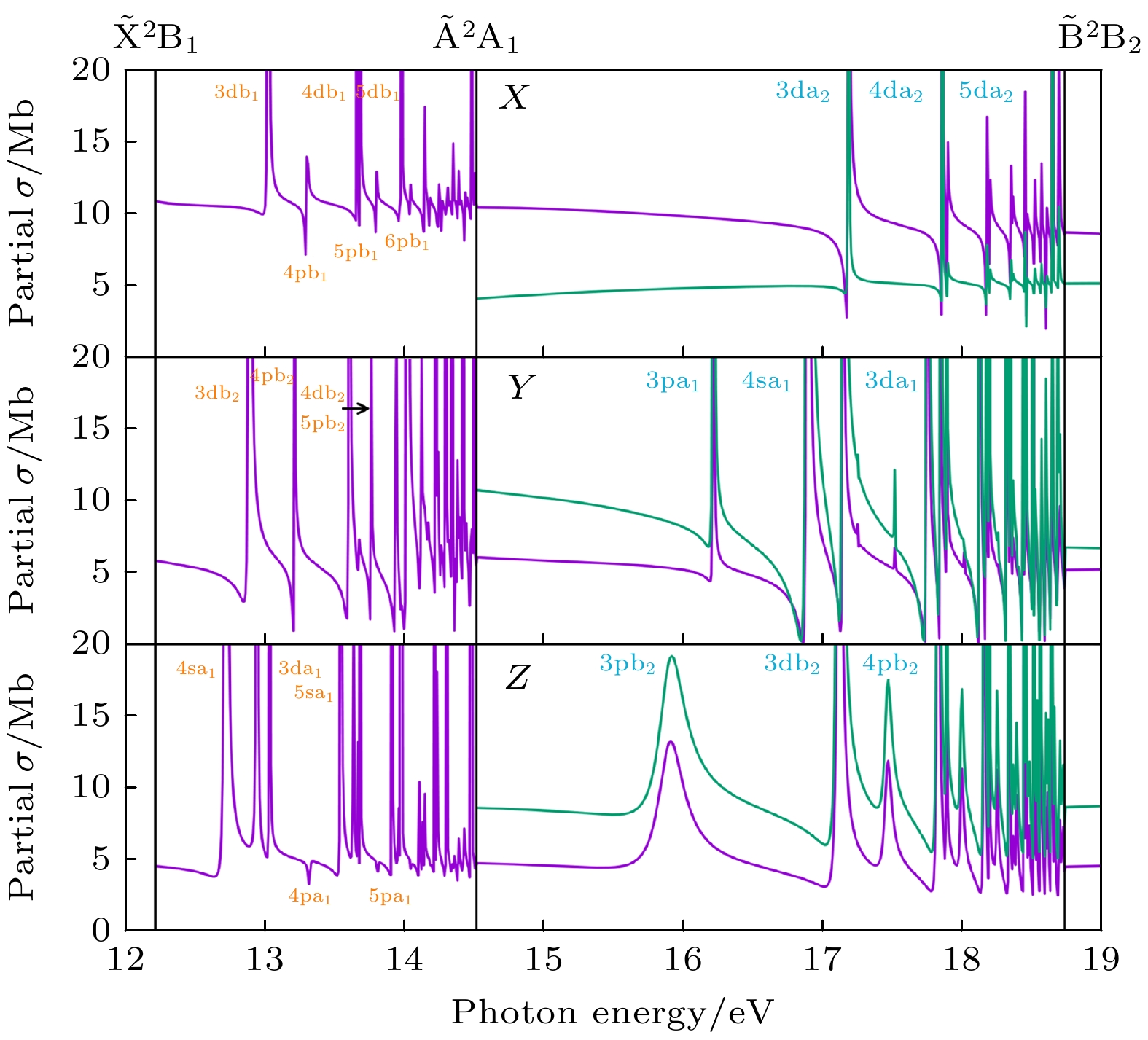
图 7 对应于$ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1}({\mathrm{紫}}{\mathrm{色}}{\mathrm{线}}) $和$ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1}({\mathrm{绿}}{\mathrm{线}}) $电离通道的部分截面. 结果考虑了12—19 eV的能量区间, 且利用XCHEM方法在长度规范下完成 (a) 沿着X方向极化的部分截面[32]; (b) 沿着Y方向极化的部分截面[32]; (c) 沿着Z方向极化的部分截面. 收敛到$ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $和$ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $阈值的自电离态分别用橙色和蓝色标注在图中[32]
Fig. 7. Partial cross sections for (purple line) $ \widetilde{{\mathrm{X}}}{}^{2}{{\mathrm{B}}}_{1} $ and (green line) $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $ ionization channels in the energy region 12–19 eV, calculated with XCHEM in the length gauge: (a) Partial cross sections for polarization along the X directions[32]; (b) partial cross sections for polarization along the Y directions[32]; (c) partial cross sections for polarization along the Z directions. Labels of autoionizing states converging to the $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $ threshold are indicated in orange and those converging to $ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $ in blue[32].
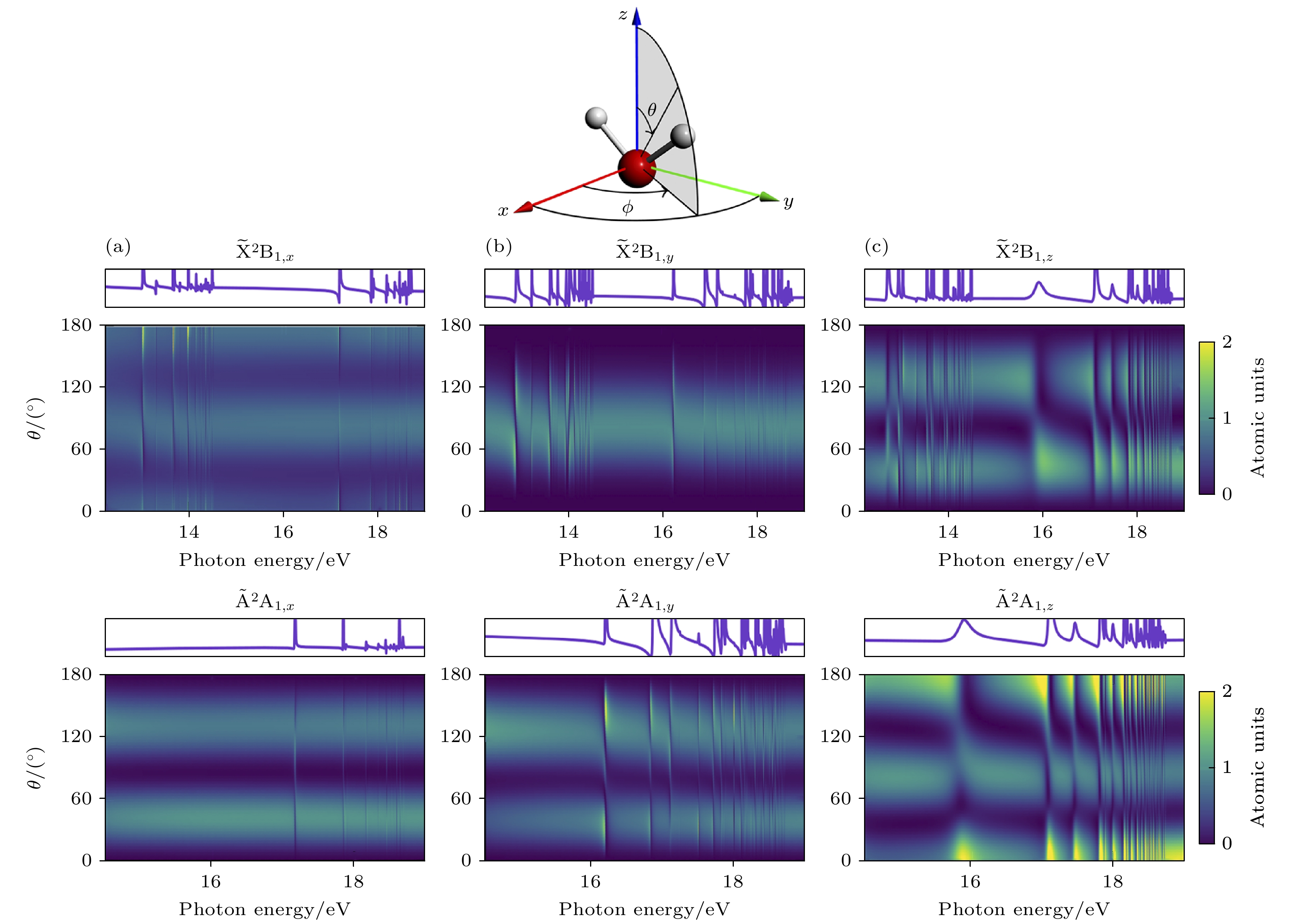
图 8 对应x (a), y (b)和z (c)方向极化的对于方位角ϕ积分后得到的不同光子能量和电子发射角θ的光电子谱[32]
Fig. 8. Photoelectron spectra as a function of photon energy and the electron emission angle θ obtained after integrating over the azimuthal angle ϕ panels: (a) x polarization[32]; (b) y polarization[32]; (c) z polarization. The corresponding θ and ϕ integrated partial cross sections are shown on top of each panel[32].
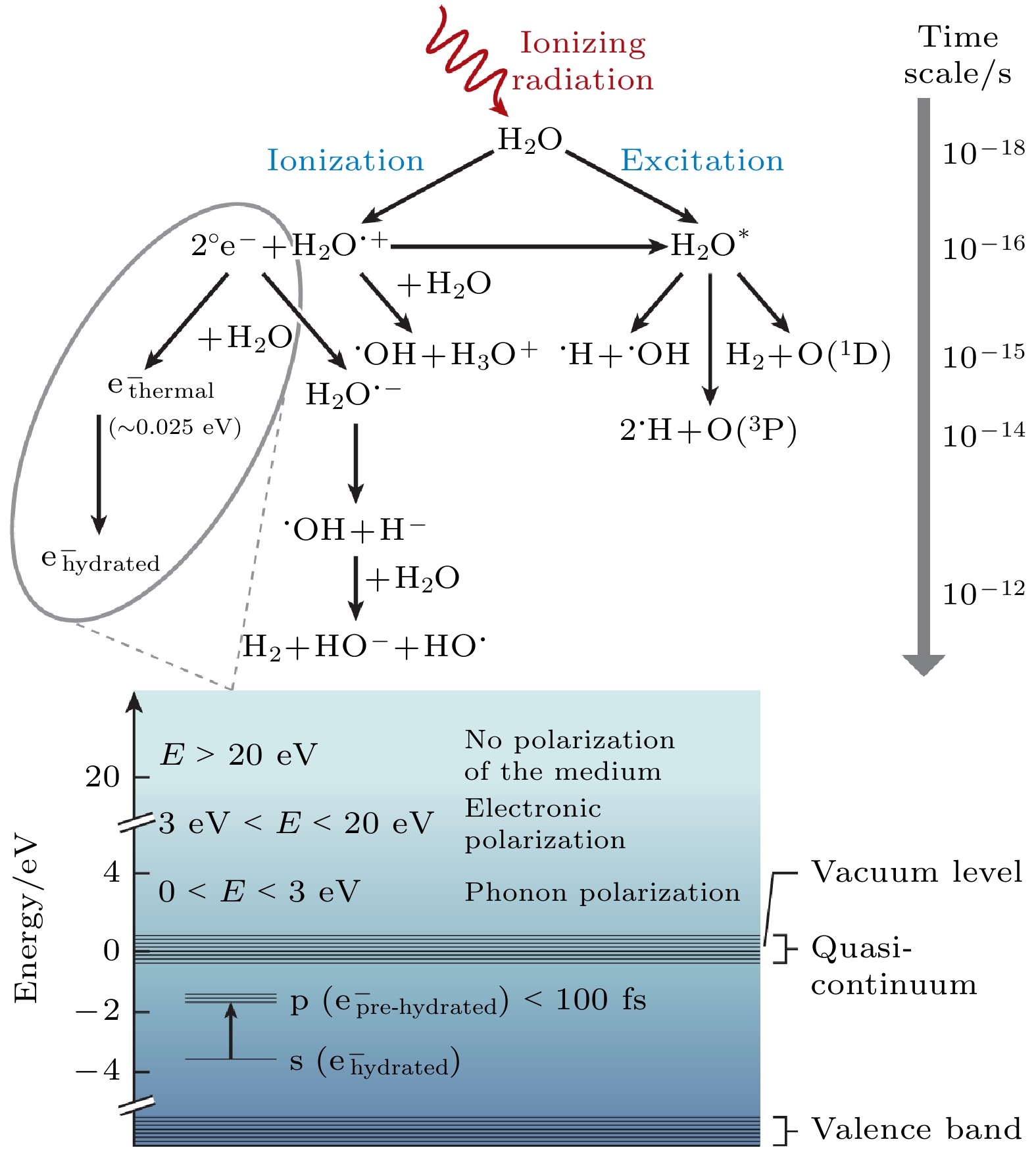
图 9 水的辐射分解示意图. 电离辐射会产生自由基中间体 $ {{\mathrm{e}}}^{-} $(aq), H· 和HO·. 图的下部显示了体相水中 $ {{\mathrm{e}}}^{-} $(aq)的能级图[17]
Fig. 9. Schematic overview of water radiolysis, wherein ionizing radiation generates radical intermediates $ {{\mathrm{e}}}^{-} $(aq), H·, and HO·. An energy-level diagram of $ {{\mathrm{e}}}^{-} $(aq) in bulk water is depicted in the lower part of the figure[17].
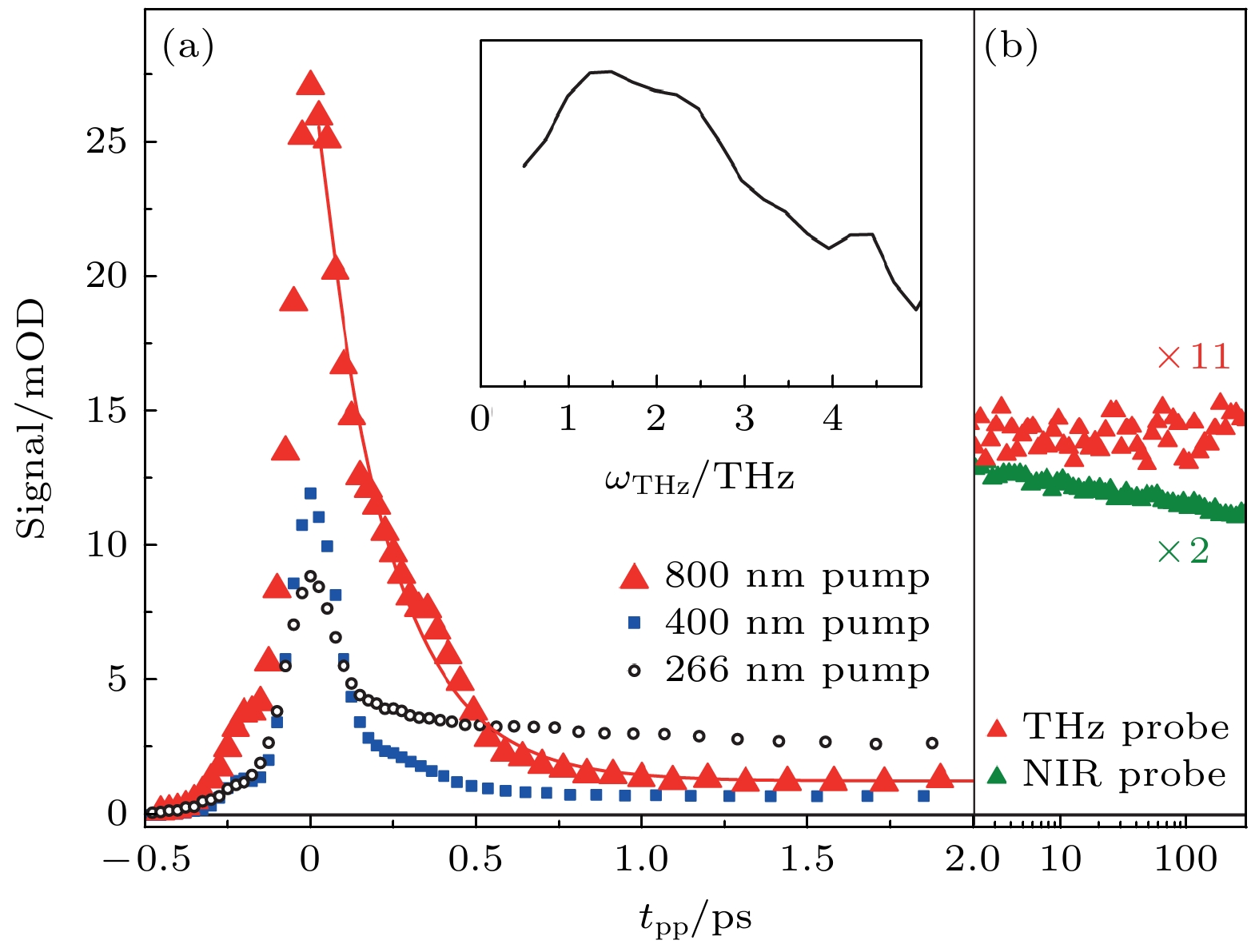
图 10 纯水光电离的太赫兹响应 (a) 800 nm泵浦(红色三角形)与单指数拟合结果(200 fs, 红线)、400 nm泵浦(蓝色填充方形)和266 nm泵浦(黑色开口圆圈)的结果. 400和266 nm波长的泵浦轨迹以800 nm波长泵浦的水合电子($ {{\mathrm{e}}}_{{\mathrm{a}}{\mathrm{q}}}^{-} $)浓度进行了缩放. 插图: 通过二维扫描推导出的 800 nm泵浦时过量电子的光谱特征. 该初始光谱在约1.5 THz处达到峰值[18]. (b) 使用 800 nm泵浦(红色, 按 11 倍缩放)的长时间太赫兹响应保持不变, 而在近红外条件下探测到的响应则清楚地显示了成对重组的动力学[18]
Fig. 10. Terahertz response to photoionization of neat water. (a) The 800 nm pump (red triangles) with a single exponential fit (200 fs, redline), 400 nm pump (blue filled squares) and 266 nm pump (open black circles). The 400 and 266 nm pump traces are scaled to the $ {{\mathrm{e}}}_{{\mathrm{a}}{\mathrm{q}}}^{-} $ concentration in the 800 nm pump measurement. Inset: spectral signature of the excess electron upon 800 nm pumping deduced from a two-dimensional scan. This initial spectrum peaks at ~1.5 THz[18]. (b) The long-time terahertz response with the 800 nm pump (red, scaled by factor of 11) remains constant, whereas the response probed at NIR shows clearly the geminate recombination kinetics (green) [18].
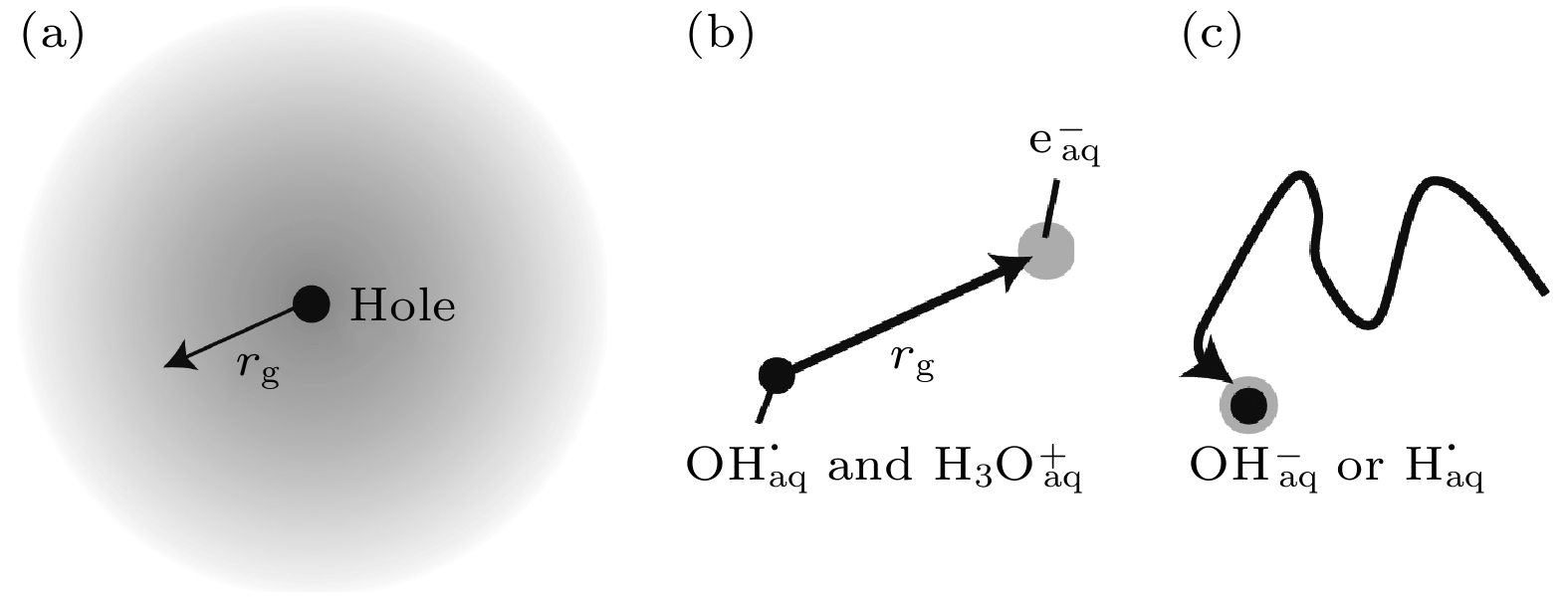
图 11 过剩电子在水中的形成和定域过程示意图 (a) 辐射出的局部过剩电子(灰色), 半径为rg[18]; (b) 电子波函数的坍缩, 这将导致平均迁移长度为rg[18]; (c) 扩散性成对重组[18]
Fig. 11. Schematic depiction of excess electron formation and localization process in water: (a) Ejected delocalized excess electron (in grey) with radius rg[18]; (b) collapse of the electron wavefunction, which will result in an average ejection length rg[18]; (c) diffusive geminate recombination[18].
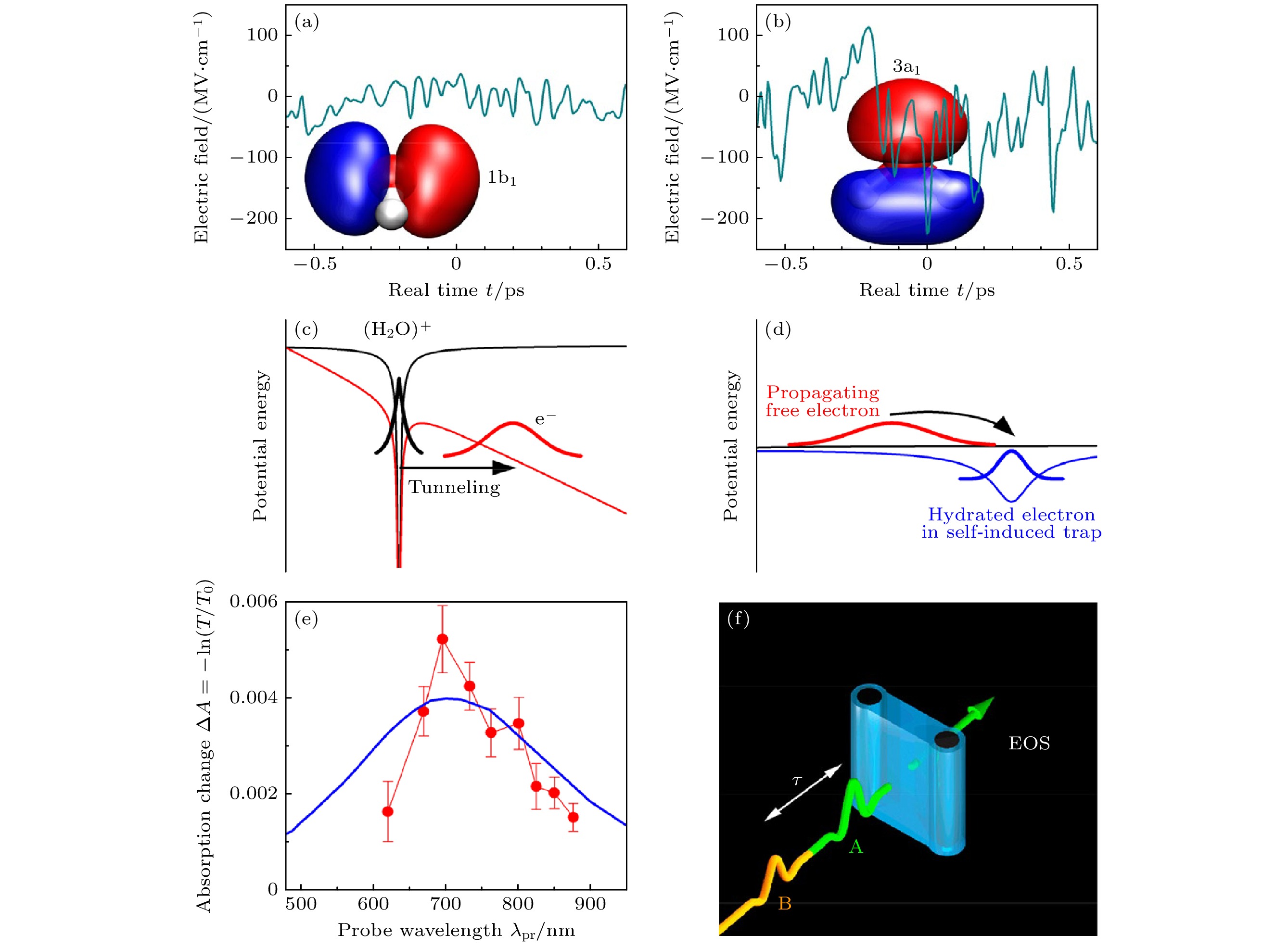
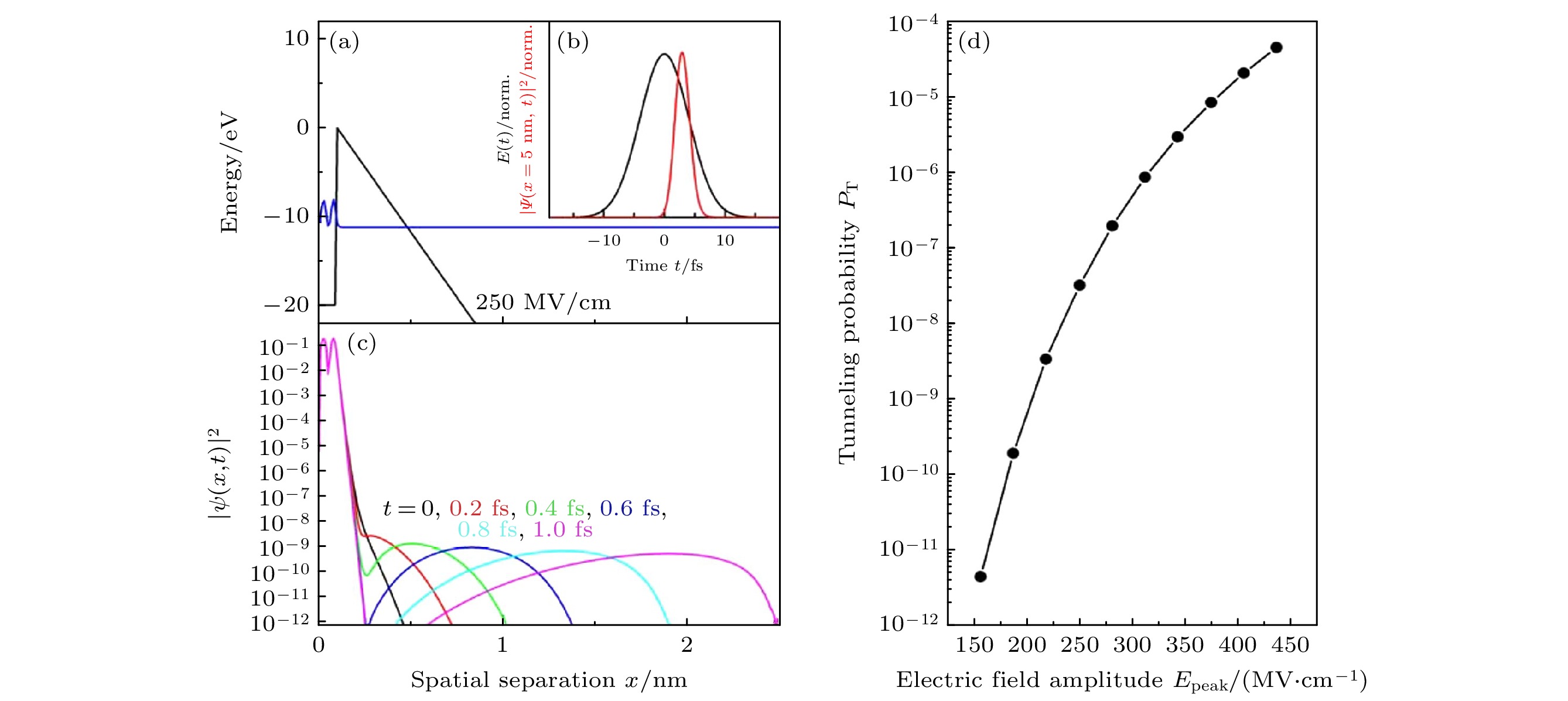
图 12 水的场致电子动力学和非线性二维太赫兹(2D-THz)光谱 (a), (b) 分子动力学模拟计算出的液态水中电子在两个最高占位轨道1b1 (HOMO)和3a1 (HOMO-1)位置的波动电场[19]; (c) 场致电子隧道示意图[19]; (d) 电子传播和定域化示意图[19]; (e) 水样品在与峰值场EA,P = 1.9 MV/cm太赫兹泵浦脉冲相互作用后, 在延迟时间τ = 300 ps 时的近红外吸收变化ΔA = –ln(T/T0), 蓝线: 溶解电子的缩放吸收光谱[19]; (f) 采用锁相太赫兹技术的二维太赫兹实验示意图. 水射流(蓝色)的形状, 以及通向电光采样(EOS)的路径[19]
Fig. 12. Two-dimensional terahertz (2D-THz) spectroscopy: (a), (b) Fluctuating electric fields in liquid water as calculated from a molecular dynamics simulation for electrons at the position of the two highest occupied orbitals 1b1 (HOMO) and 3a1 (HOMO-1) [19]; (c) schematic diagram of field-induced electron tunneling[19]; (d) schematic of electron propagation and localization[19]; (e) near-infrared absorption change ΔA = –ln(T/T0) of the water sample at a delay time of τ = 300 ps after interaction with a THz pump pulse of a peak field EA,P = 1.9 MV/cm transmitted through the sample (symbols, T, T0: sample transmission with and without excitation, blue line: Scaled absorption spectrum of solvated electrons)[19]; (f) schematic of the 2D-THz experiment with phase-locked THz pulses A and B of delay τ, the water jet (blue) in transmission geometry, and the path toward the electrooptic sampling (EOS) detector[19].
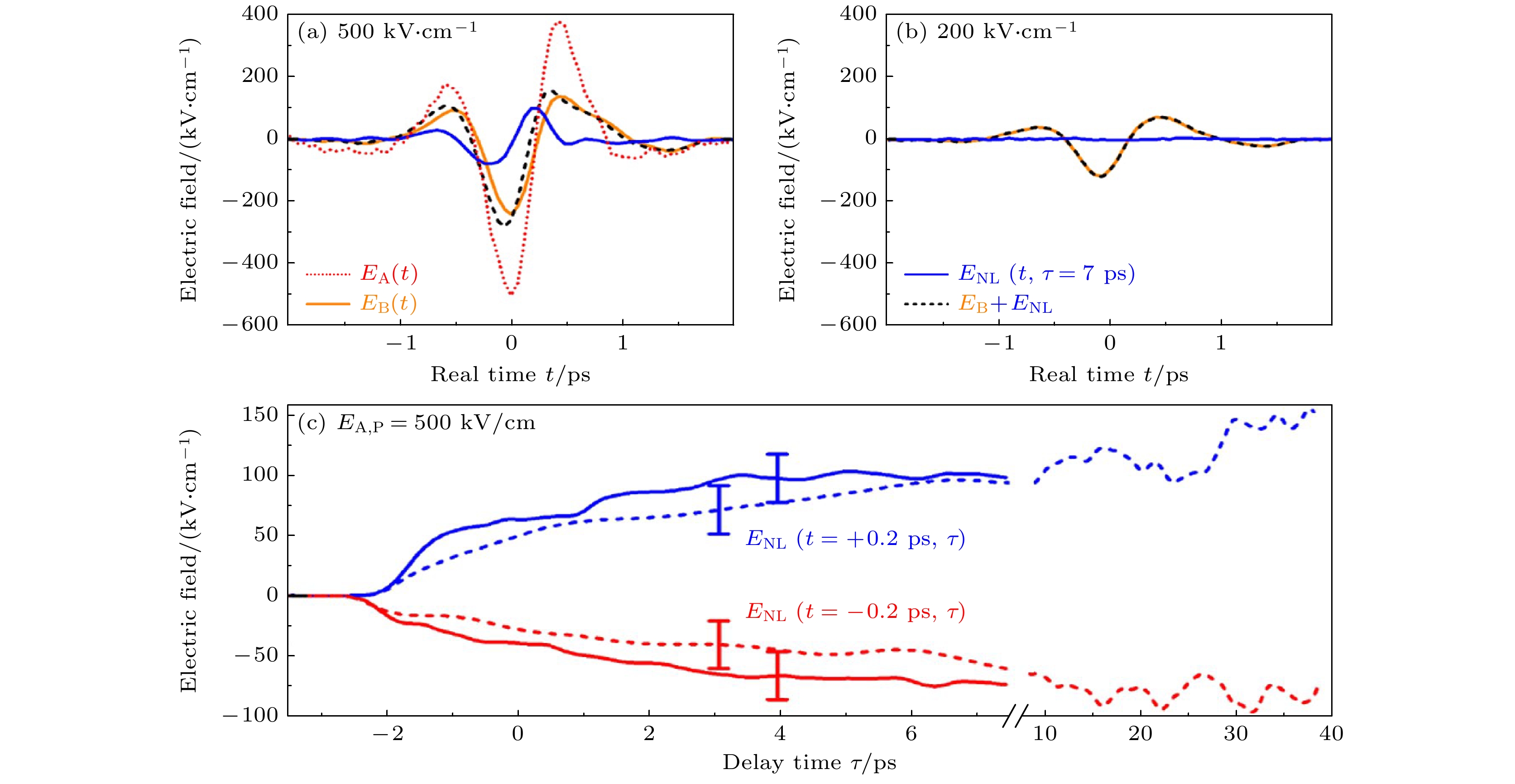
图 13 时间分辨非线性太赫兹响应 (a), (b) 延迟时间为 τ = 7 ps时的非线性信号场ENL(t, τ = 7 ps)(蓝线)、探测场 EB(t)(橙色线)以及二者的和EB,T(t, τ = 7 ps) = EB(t) + ENL(t, τ = 7 ps)(黑色虚线)都是入射脉冲A峰值振幅为EA,P = 500, 200 kV/cm时真实时间t的函数. 场EB,T(t, τ = 7 ps)代表通过激发样品传输的总THz探针场. 图(a)中的红色虚线表示传输的泵浦场EA(t) [19]. (c) 非线性信号场ENL(t = ±0.2 ps, τ)作为在泵浦电场峰值振幅EA,P = 500 kV/cm下, t = –0.2 ps (图(a)中的红色实线, 信号最小值)和t = +0.2 ps (图(a)中的蓝色实线, 信号最大值)时的延迟时间 τ 的函数. 虚线来自通过稍微改变泵浦场条件, 进行的符合实验精度范围(误差条)且有更长的延迟时间τ的轨迹[19]
Fig. 13. Time-resolved nonlinear THz response. (a), (b) Nonlinear signal field ENL(t, τ = 7 ps) (blue line) for a delay time of τ = 7 ps together with the probe field EB(t) (orange line) and the sum EB, T(t, τ = 7 ps) = EB(t)+ENL(t, τ = 7 ps) (black dashed line) as a function of real time t for peak amplitudes EA, P = 500, 200 kV/cm of incoming pump pulse A. Field EB, T(t, τ = 7 ps) represents the total THz probe field transmitted through the excited sample. The dotted red line in panel (a) shows the transmitted pump field EA(t) [19]. (c) Nonlinear signal field ENL(t = ±0.2 ps, τ) as a function of delay time τ for t = –0.2 ps (red solid line, signal minimum in panel (a)) and t = +0.2 ps (blue solid line, signal maximum in panel (a)) for a pump field amplitude EA, P = 500 kV/cm. The dashed lines from an independent measurement with a slightly different pump field agree with the experimental accuracy (error bars) and extend to longer delay times τ [19].
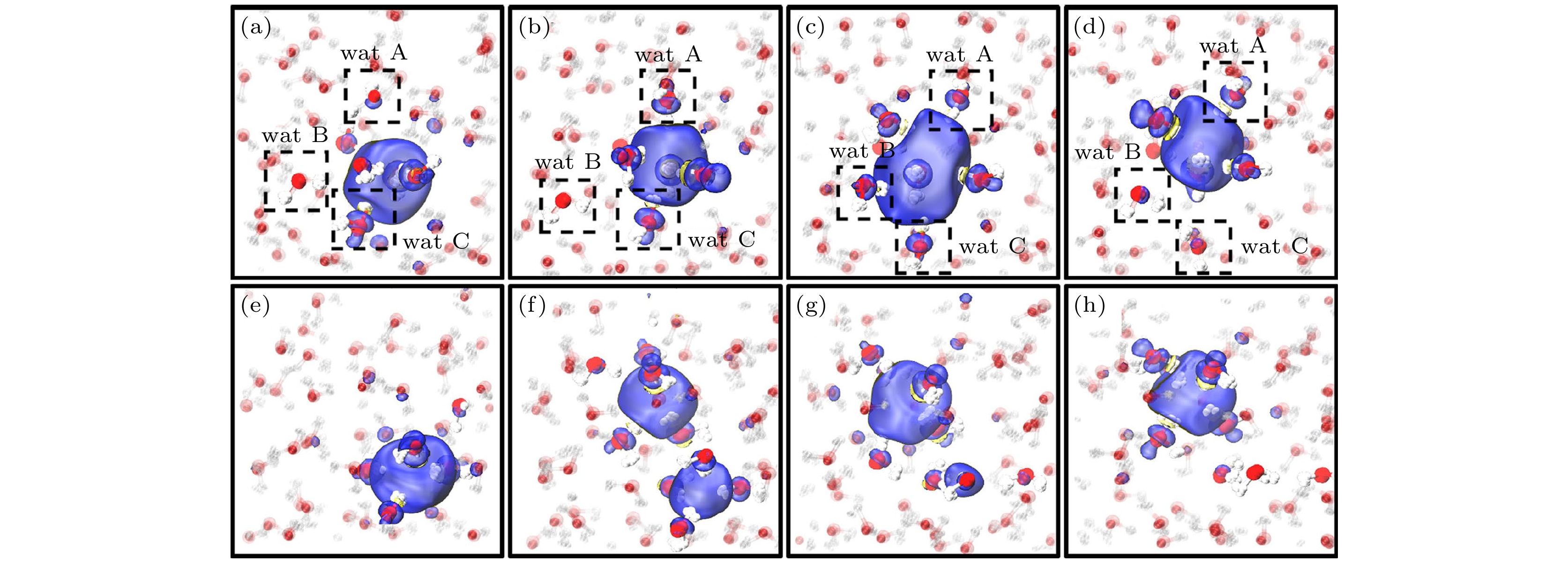
图 15 非瞬态(上)和瞬态(下)扩散机制. 自旋密度用蓝色(正)和黄色(负)表示. 非瞬态机理是由形成空腔的分子与其相邻的无键水分子之间形成氢键(HBs)而引发的(在图(a)—(d)中以A和B表示). 随后A, B的悬空氢氧根与空腔中的水合电子结合, 取代了第三个分子C(图(c)). 分子B和C与它们的邻居形成HBs, 并从空腔中脱离(图(d)). 瞬态扩散(图(e)至(h))为特点是存在双腔(图(f))[25]
Fig. 15. Non-transient (top) and transient (bottom) diffusion mechanisms. Spin densities are shown in blue (positive) and yellow (negative). Non-transient mechanism is initiated by the formation of the hydrogen bonds (HBs) between a cavity-forming molecule and its unbonded neighboring water molecules (indicated as A and B in panels (a)–(d)). The dangling OH of A, B subsequently binds to the hydrated electron in the cavity, replacing that of a third molecule, C (panel (c)). Molecules B and C form HBs with their neighbors, and unbind from the cavity (panel (d)). Transient diffusion (panels (e) to (h)) is characterized by the existence of the double-cavity (panel (f))[25].
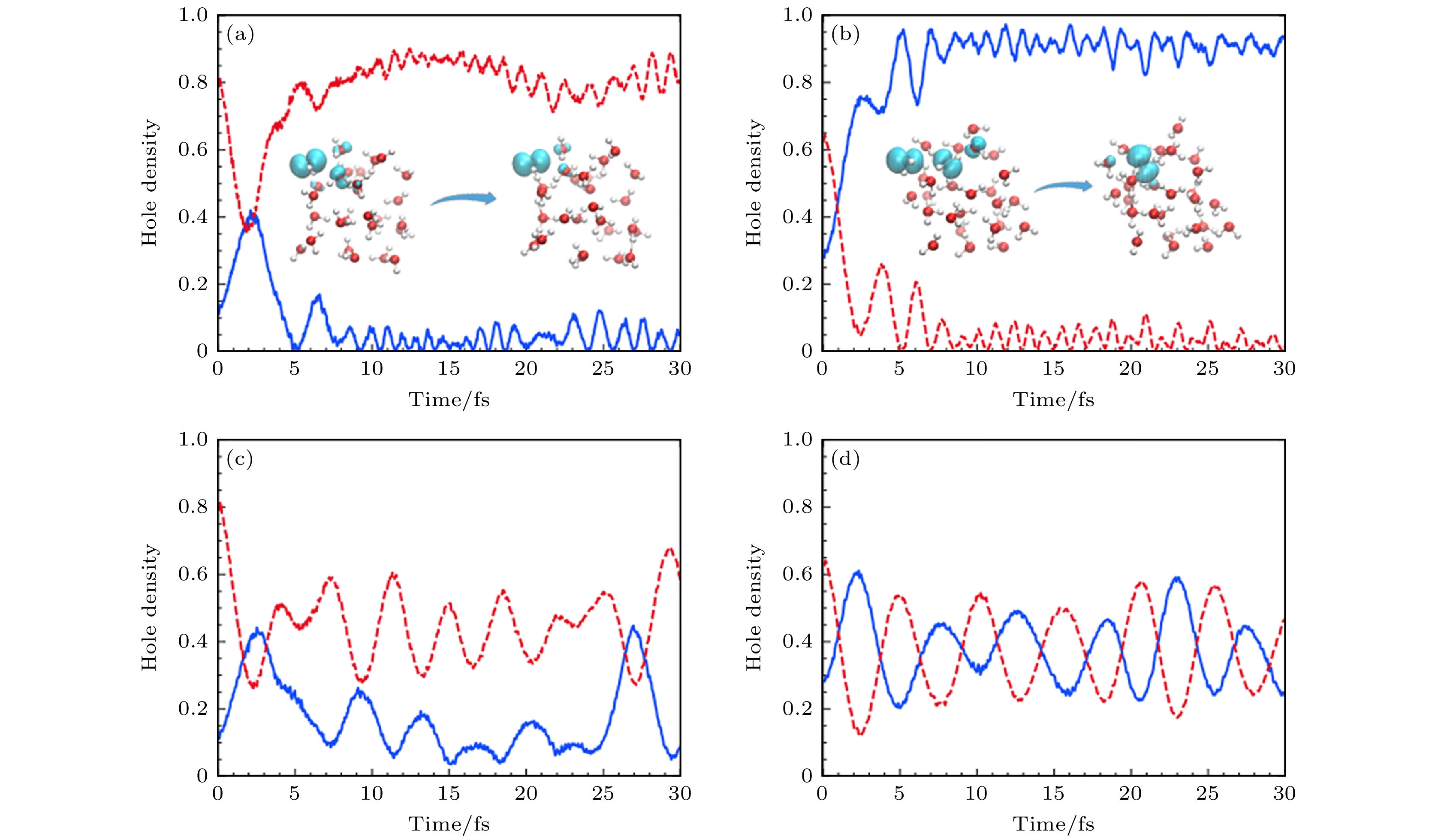
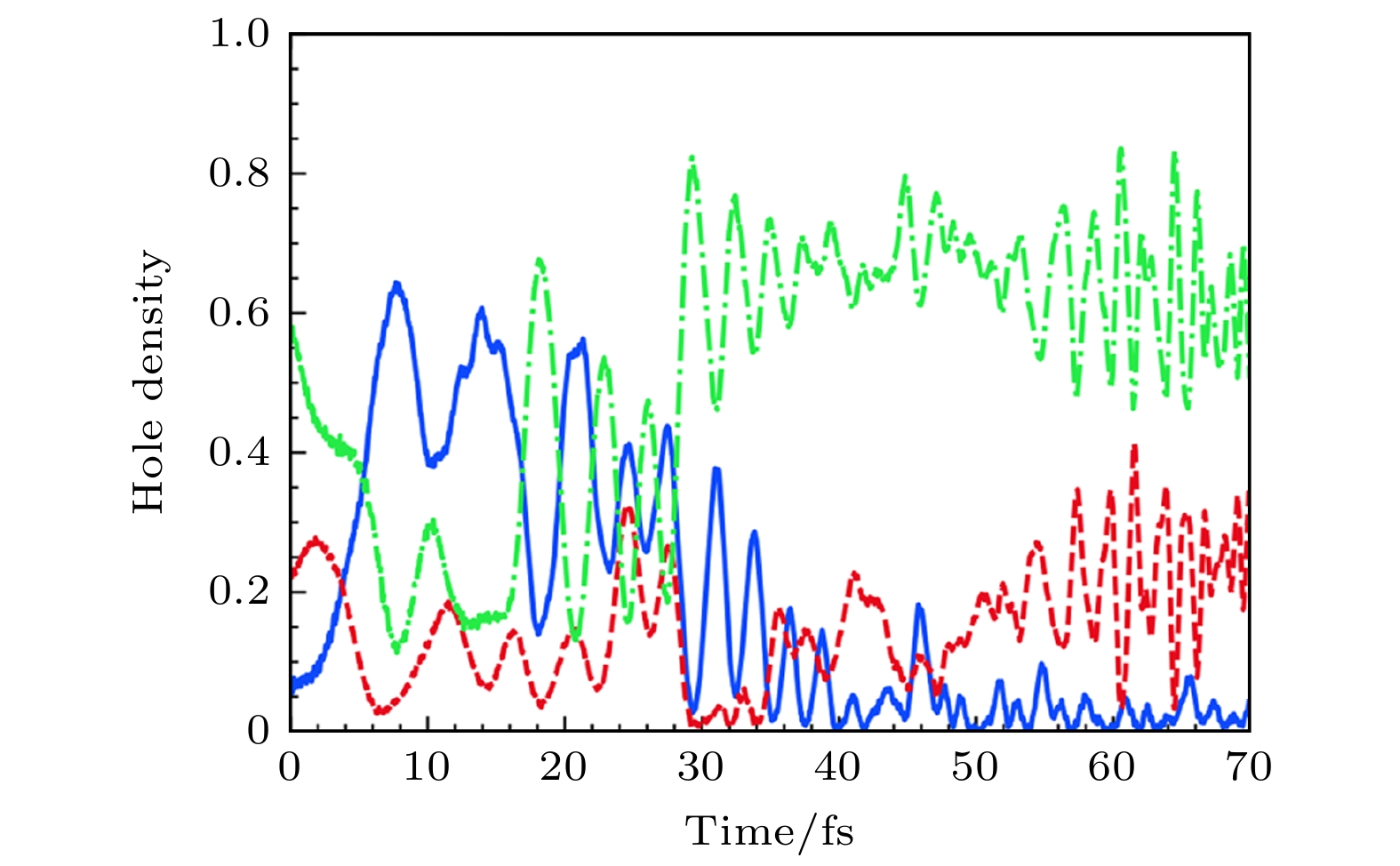
图 16 (a), (b)采用从头算Ehrenfest动力学的选择模拟的时间分辨空穴密度图[16]; (c), (d)固定核实时电子动力学, 初始条件分别与子图(a)和图(b)相同. 空穴密度是用在氧原子上的Mulliken自旋密度来计算的, 绘制的是两个最大的空穴密度[16]
Fig. 16. (a), (b) Time-resolved hole density plots of selected simulations using ab initio Ehrenfest dynamics[16]; (c), (d) fixed-nucleus real-time electronic dynamics using the same initial conditions as in panels (a) and (b), respectively. Hole densities are computed as Mulliken spin densities projected on oxygen atoms. The two largest hole densities are plotted[16].
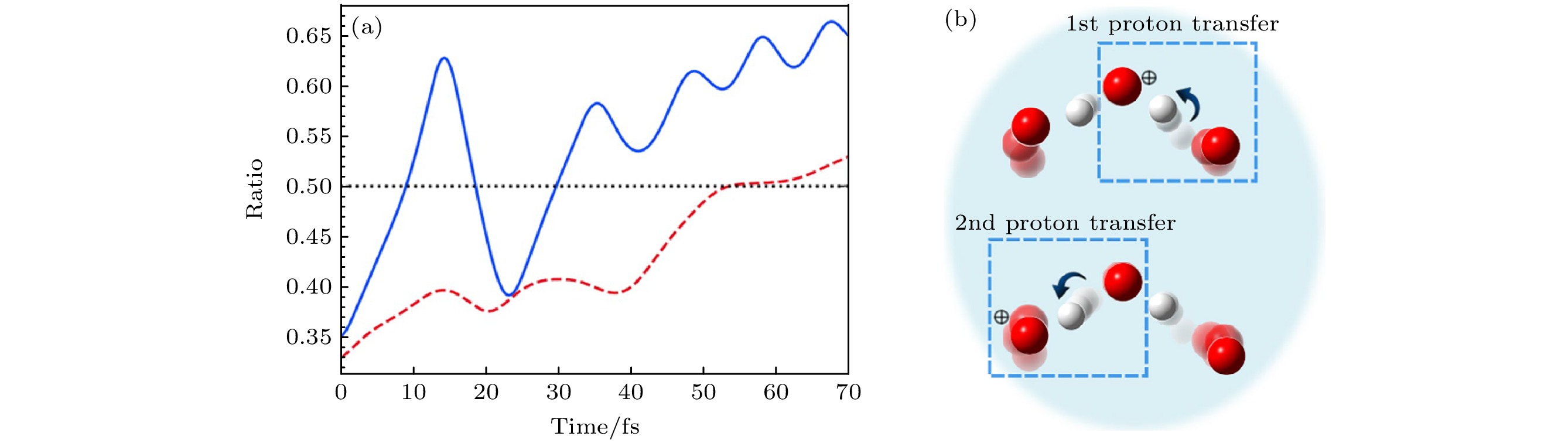
图 17 (a)电离后轨迹b (和图16(b)中的轨迹一致)的从头算Ehrenfest动力学比图, 表示第一(蓝色, 实线)和第二(红色, 虚线)质子转移过程[16]; (b)第一和第二质子转移示意图[16]
Fig. 17. (a) Ratio plots of ab initio Ehrenfest dynamics for trajectory b (same as that in Fig. 16(b)) after the ionization, indicating the first (blue, solid) and second (red, dashed) proton transfer processes[16]; (b) illustrations of the first and second proton transfers[16]
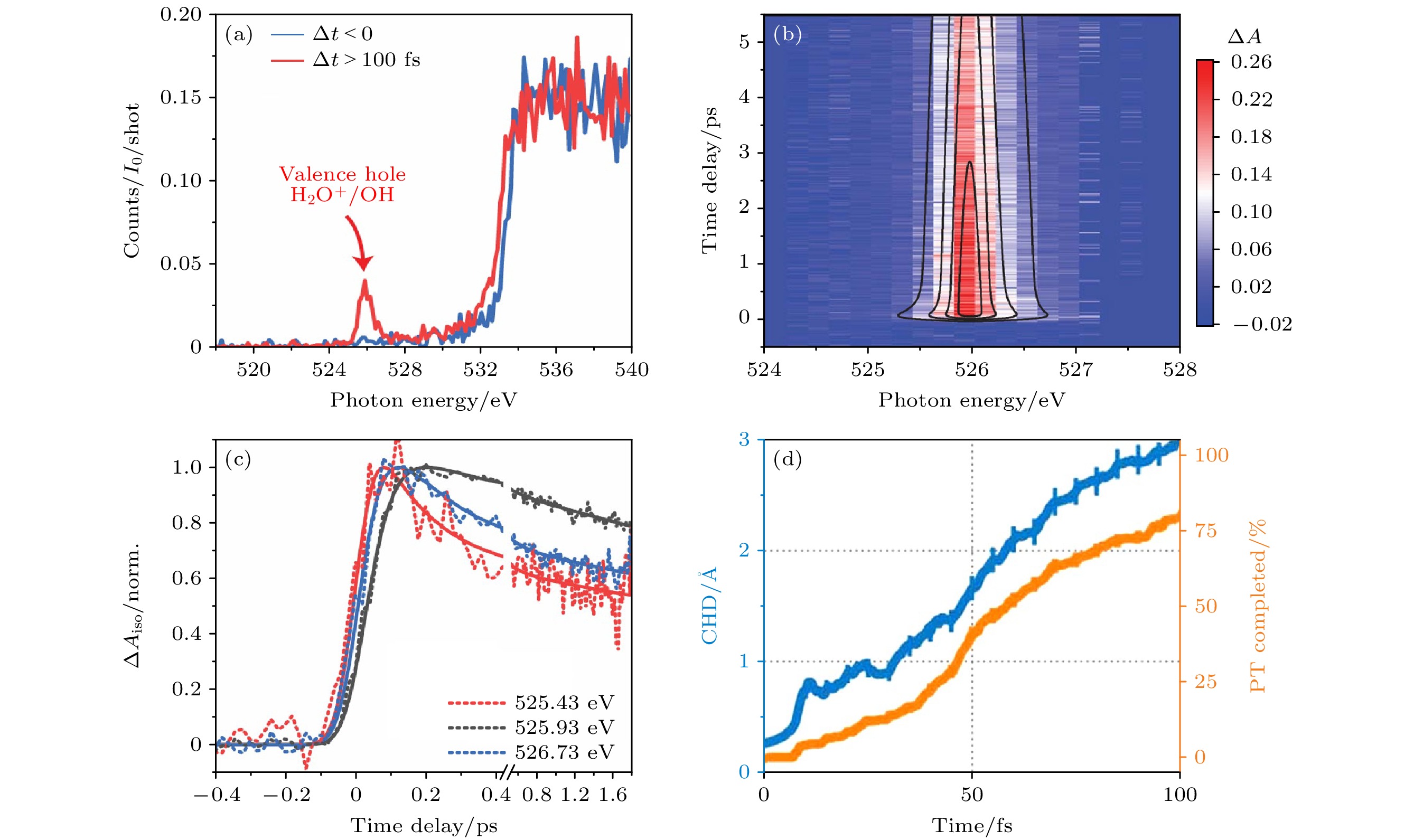
图 19 (a) 通过分散荧光通道分别对于Δt < 0和Δt > 100 fs进行探测[36]; (b) 价空穴(H2O+/OH)区微分吸收ΔA. 在1.5和5.8 ps之间的216个时间延迟中收集的光谱被平均以产生共振剖面, 该共振剖面可以用两个洛伦兹函数的和来拟合[36]; (c) 525.43, 525.93和526.73 eV三种X射线探针能量下的按极化方向平均后的时间轨迹[36]; (d) 电荷-空穴距离(CHD)(蓝色)和质子完全转移百分比(橙色)的时间演化[36]
Fig. 19. (a) Absorption for Δt < 0 and Δt > 100 fs monitored through the dispersed fluorescence channel[36]; (b) differential absorption ΔA in the valence hole (H2O+/OH) region. Spectra collected at 216 time delays between 1.5 and 5.8 ps are averaged to produce the resonance profile, which is fit to a sum of two Lorentzians[36]; (c) polarization averaged time traces at three X-ray probe energies: 525.43, 525.93, and 526.73 eV[36]; (d) charge-hole distance (CHD) (blue) and completed proton transfer percentage (orange)[36]
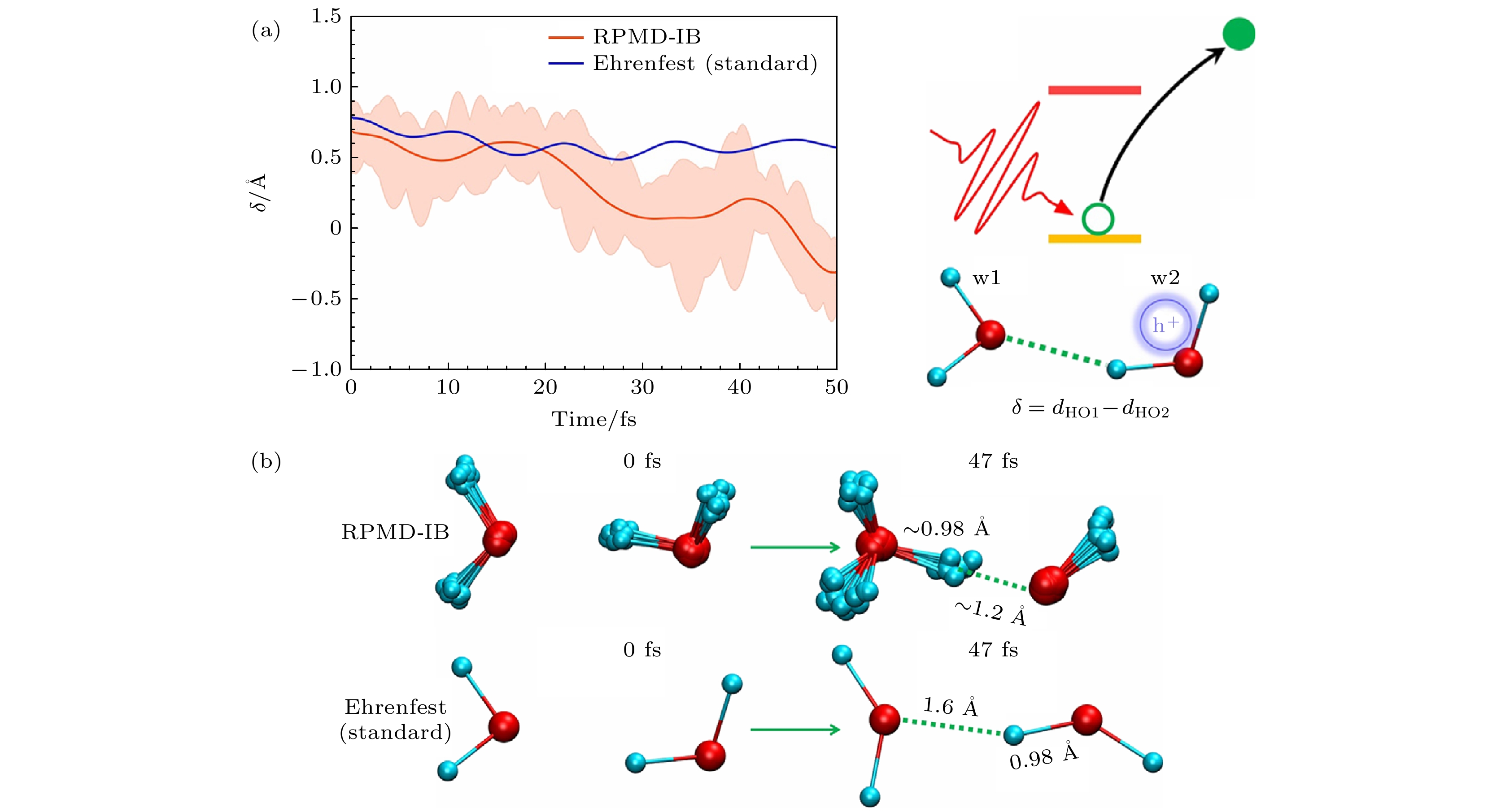
图 20 (a)氢原子(H)和离它最近的两个氧原子(O1, O2)的距离差. 阴影表示所有珠子的量子涨落. 右侧是过程的示意图[39]. (b) 激发态动力学中0和47 fs的快照. 在RPMD-IB仿真中, 给出了所有珠子的构型. 在47 fs时, 劈裂的氢原子的完整核波包接近第一个水分子的氧原子(O1), 表明水合氢离子(H3O+)和OH·自由基的形成[39]
Fig. 20. (a) The distance difference of the hydrogen atom (H) and its two nearest oxygen atoms (O1, O2). Shadows indicate the quantum fluctuation of all beads. Schematic setting is shown in the right panel[39]. (b) The snapshots at 0 and 47 fs in the excited state dynamics. In the RPMD-IB simulation, the configurations of all beads are presented. At 47 fs, the whole nuclear wave packet of split hydrogen atom approaches the oxygen atom (O1) of the first water molecule, indicating the formation of hydronium (H3O+) and OH· radical[39].
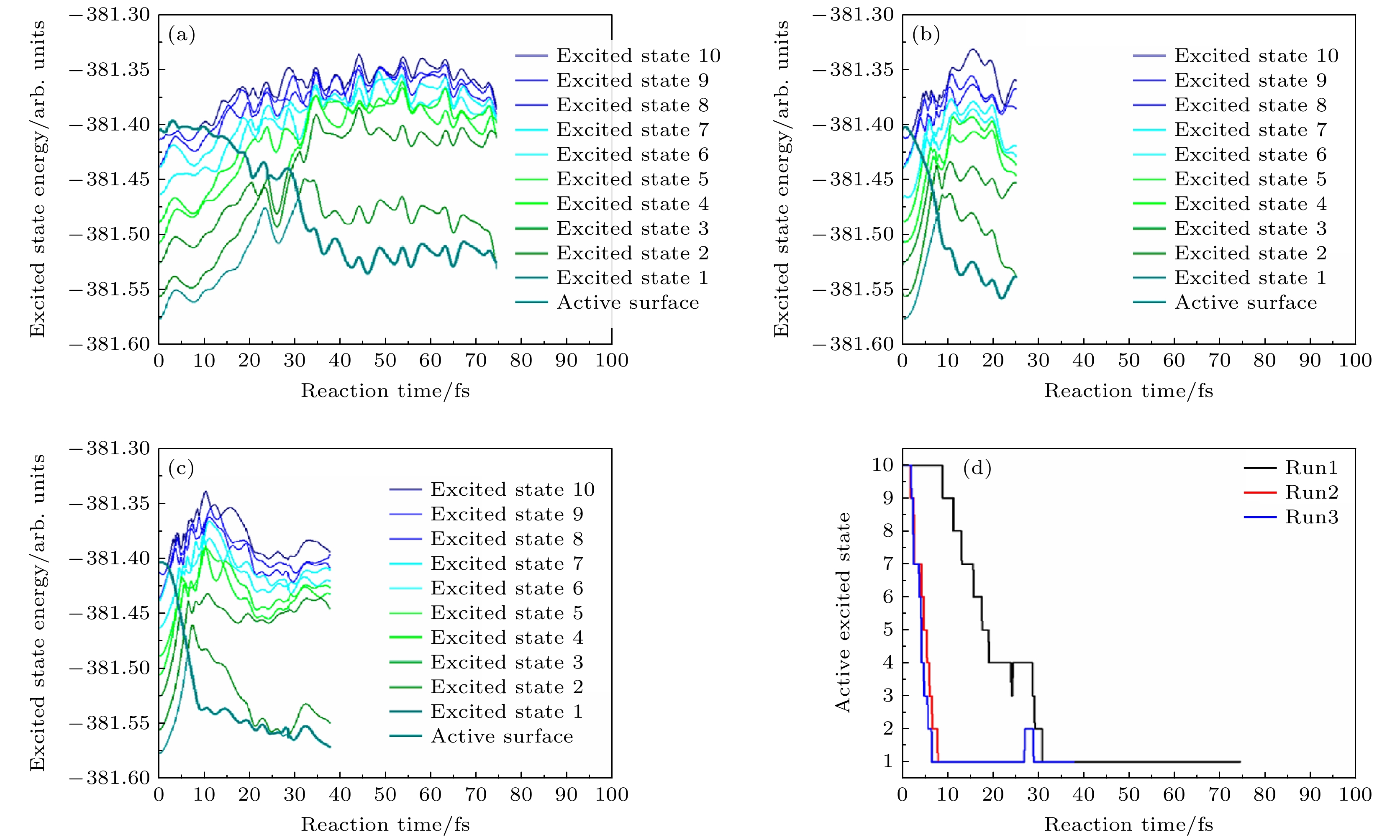
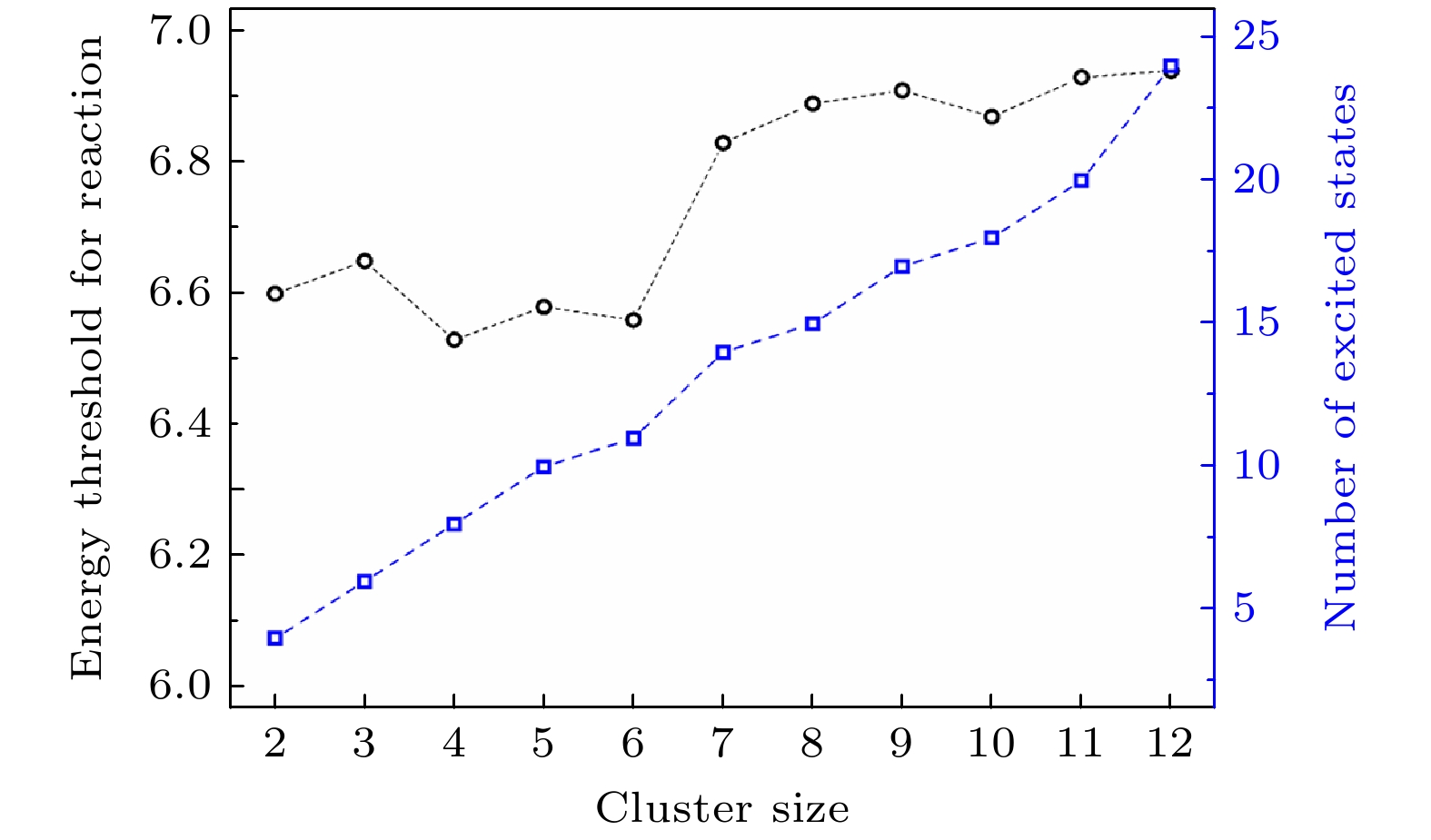
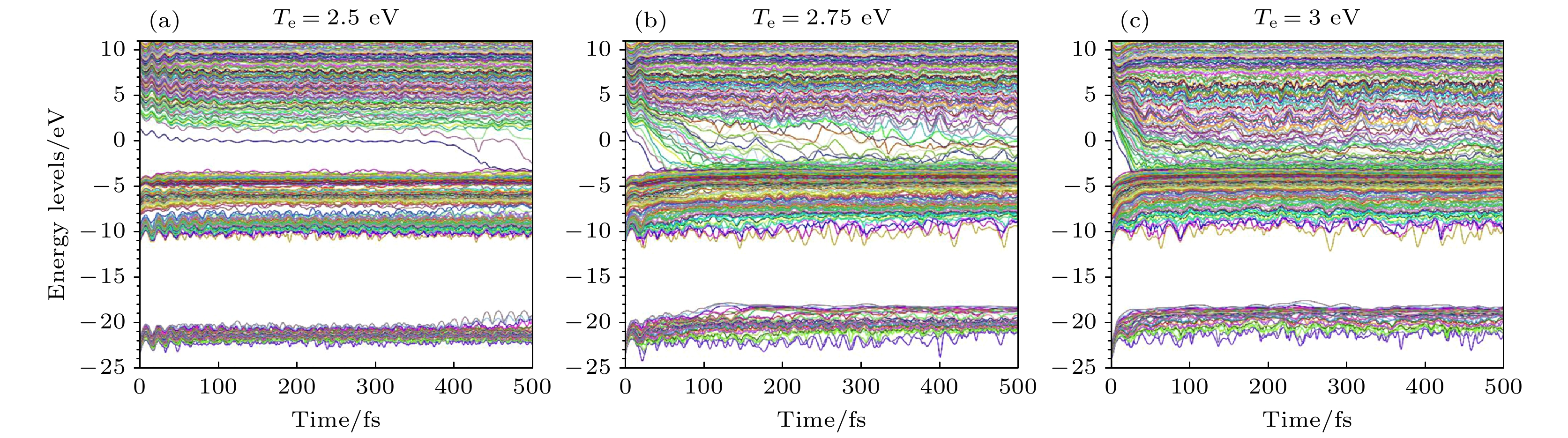
图 21 FSSH的激发态表面和活性表面分别为第1—3次轨迹(分别对应(a)—(c)), 作为时间的函数, 对于五个水分子簇和一个初始激发态被选为第10激发态的电子. 青色粗曲线表示FSSH计算中任何时刻的“活化”状态. D1, D2和更高能级之间的能量分离表明电子在OH上的状态与电子在H上的状态(对于相同的结构)是相关的[40]. (d)活性激发态表面轮廓随反应时间的变化[40]
Fig. 21. Excited state surfaces and active surface of FSSH runs 1–3 ((a)–(c), respectively) as a function of time for a cluster of five water molecules and an electron for an initial excited state chosen to be the 10 th excited state. The thick cyan curve labels the “active” state in the FSSH calculation at any time. Note that the separation in energy among D1, D2, and the higher states indicates states where the electron is on the OH are involved vs. states where the electron is on the H (for the same structure)[40]. (d) Active excited state surface profile as a function of reaction time[40].
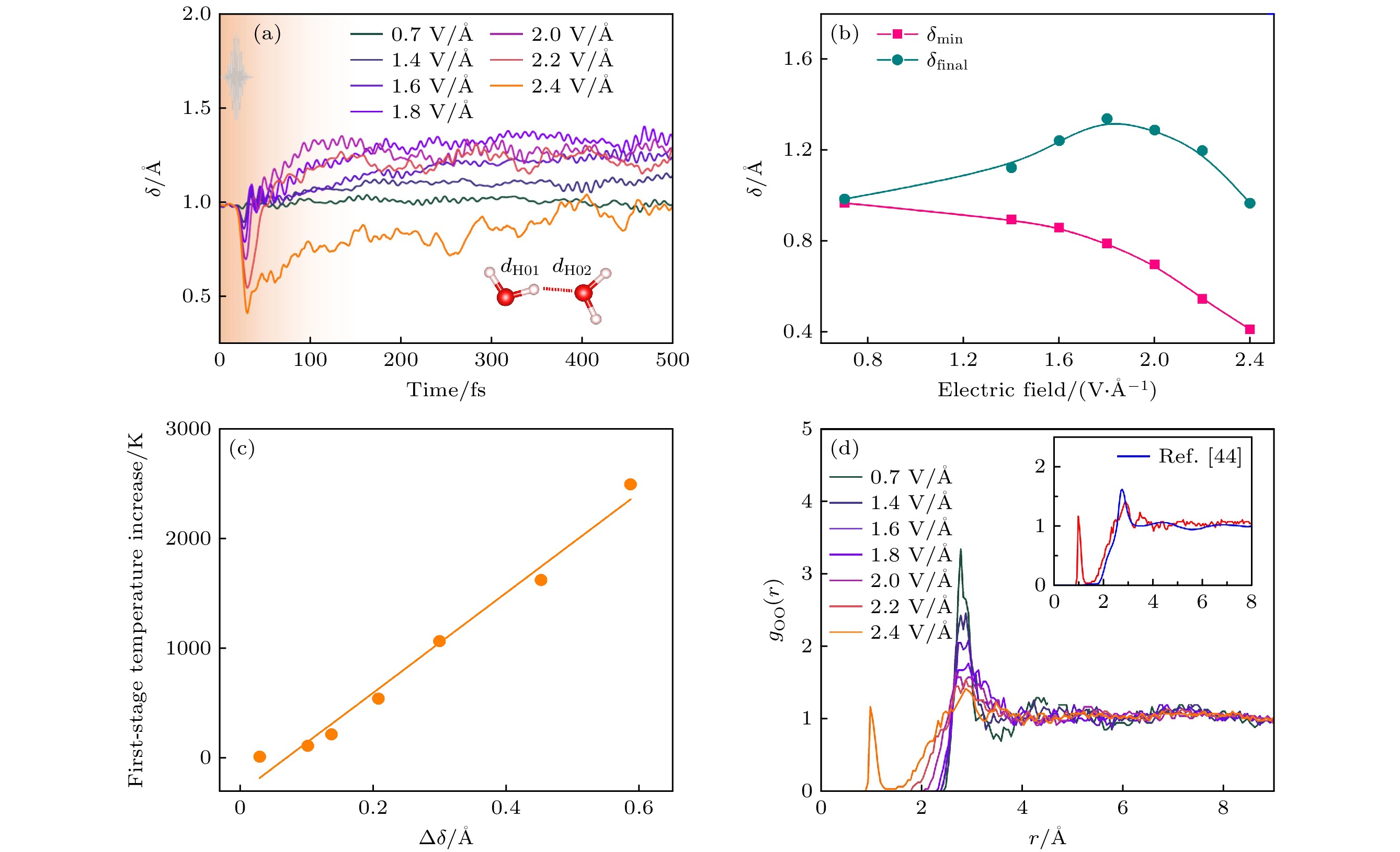
图 26 液态水的离子动力学 (a) 各氢原子平均δ随电场的时间演化. δ的定义如插图所示[26]; (b) 平均δ值和最终δ值随激光脉冲电场的变化[26]; (c) 平均δ随第一阶段离子温度的升高而降低[26]; (d) 随激光脉冲电场变化的氧-氧径向分布函数. 对每个电场进行了长达500 fs的模拟, 计算了径向分布函数. 插图显示了与参考文献[44]中的数据的比较
Fig. 26. Ionic dynamics of liquid water: (a) Temporal evolutions of average δ of all hydrogen atoms with electric field, the definition of δ is shown in the inset[26]; (b) minimum of average δ and the final δ with electric fields of laser pulses[26]; (c) decrease of average δ vs. the first-stage ionic temperature increase[26]; (d) oxygen–oxygen radial distribution functions with the electric field of laser pulses. The radial distribution functions are calculated with the whole 500 fs long simulations for each electric field[26]. The inset shows the comparison with the data from ref. [44].
图 22 加入一个热电子的五分子水团簇的超快激发态动力学中HOMO波函数的快照. 在D2→D1表面跳前后的选定时间帧拍摄快照 (a) 跳前5 fs[40]; (b) 跳时[40]; (c) 跳后5 fs[40]; (d) 跳后20 fs[40]
Fig. 22. Snapshots of the HOMO wave function during ultrafast excited state dynamics of a water cluster of five molecules with the addition of a hot electron. The snapshots are taken at selected time frames around the D2 → D1 surface hop: (a) 5 fs before the hop[40]; (b) at the hop[40]; (c) 5 fs after the hop[40]; (d) 20 fs after the hop[40].
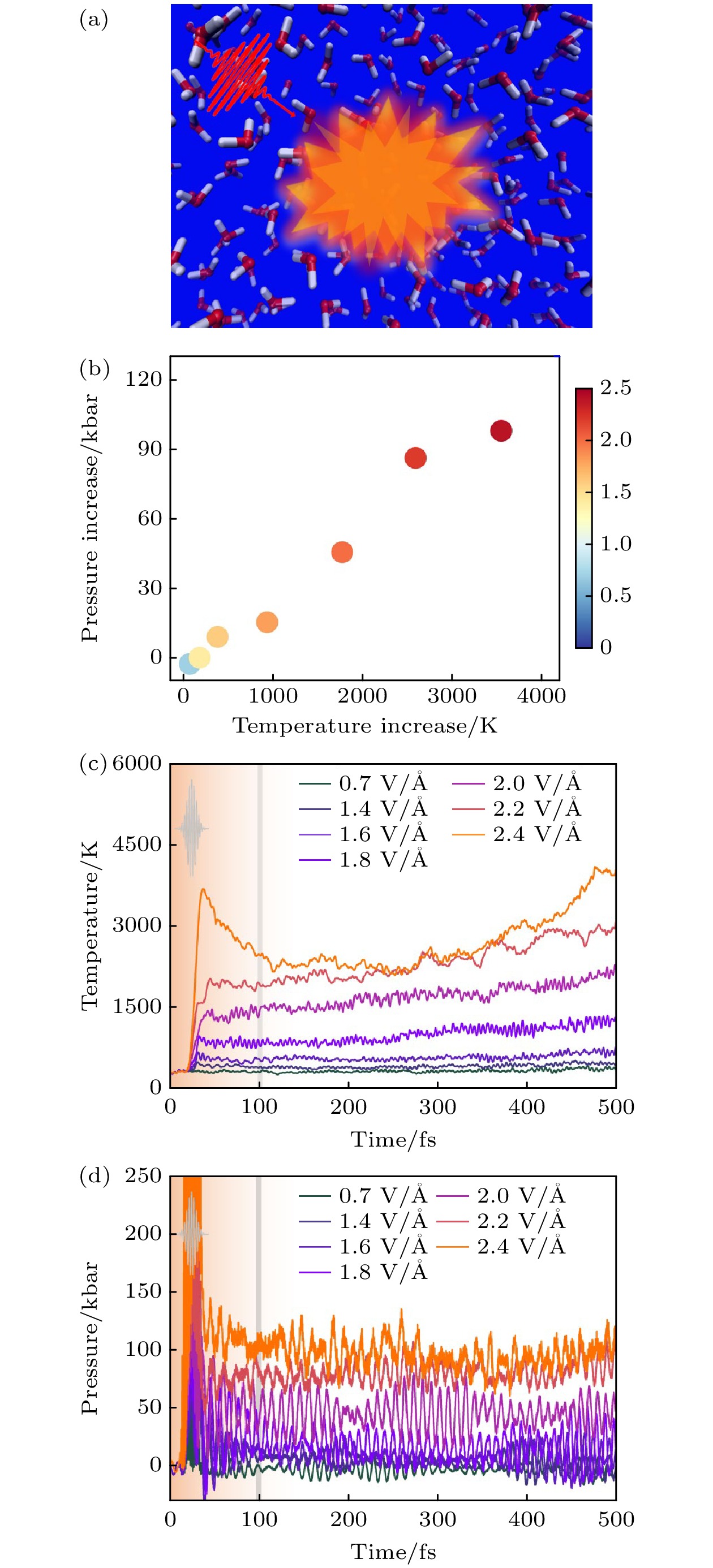
图 24 液态水的光致动力学 (a) 800 nm激光脉冲照射液态水的示意图[26]; (b) 离子温度随体系压力的增加而增加, 色条表示脉冲的电场, 单位为V/Å[26]; (c) 离子温度随激光脉冲电场的时间演变, 光场包络线如插图所示, 这条竖线标志着第一阶段和第二阶段的分离[26]; (d) 液态水的两步离子加热[26]
Fig. 24. Photoinduced dynamics of liquid water: (a) Schematic diagram shows the liquid water irradiated with the 800 nm laser pulses[26]. (b) Increase of ionic temperature versus the increase of system pressure. The colorbar shows the electric field of the pulses, and the units are V/Å[26]. (c) Temporal evolutions of ionic temperatures with the electric field of laser pulses. The light envelope is shown in the inset. The vertical line marks the separation of the first and second stage[26]. (d) Two-step ionic heating of liquid water[26]
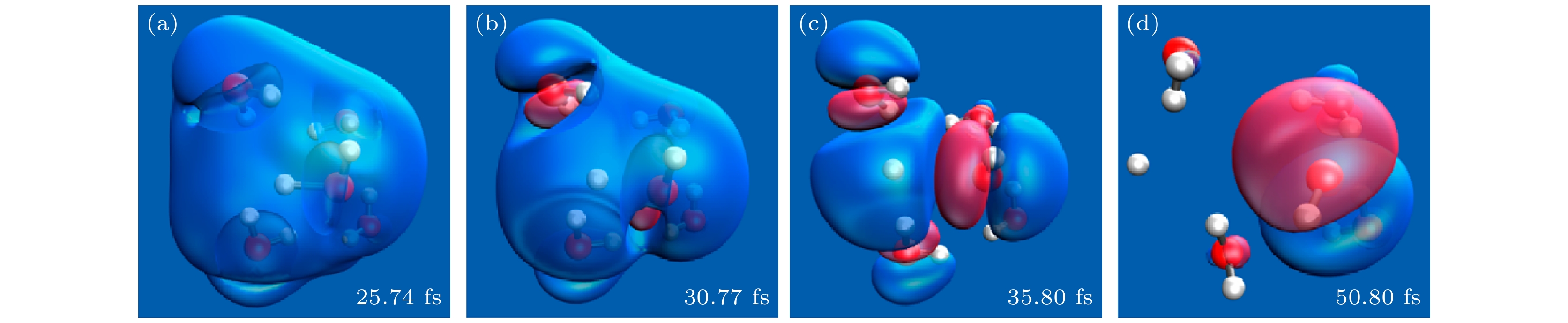
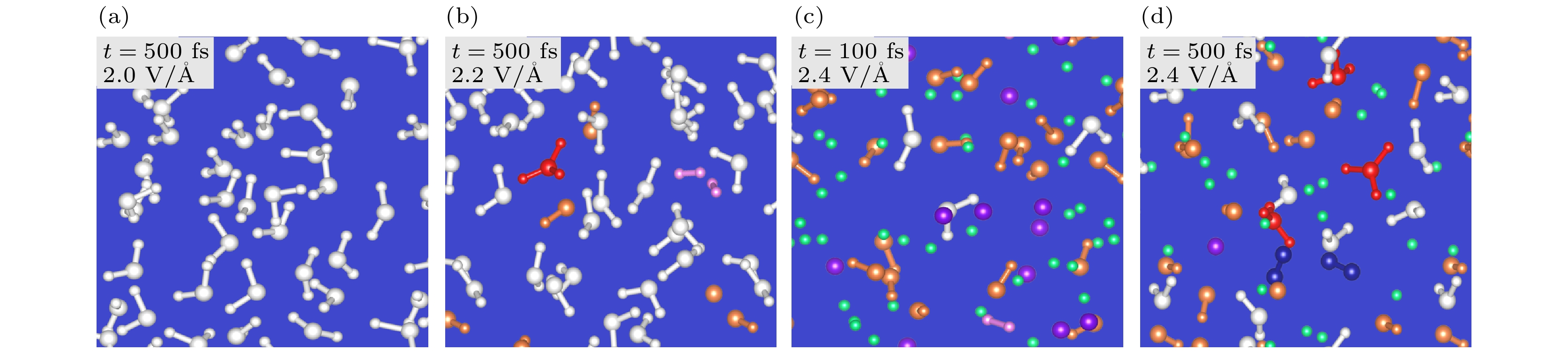
图 25 (a)—(d) 非绝热从头算分子动力学模拟构型. 激光脉冲的电场和时间如图所示. 水分子、水合离子、羟基、自由质子和氧原子、瞬态氢分子和氧分子分别显示为白色、红色、橙色、绿色、紫色、粉红色和深蓝色[26]
Fig. 25. (a)–(d) Configurations of the nonadiabatic ab initio molecular dynamics simulations. The electric field of laser pulses and the time are shown in the inset. The water molecules, hydroniums, hydroxyls, free protons and oxygens, transient hydrogen molecules, and oxygen molecules are shown in white, red, orange, green, purple, pink, and dark blue colors, respectively[26].
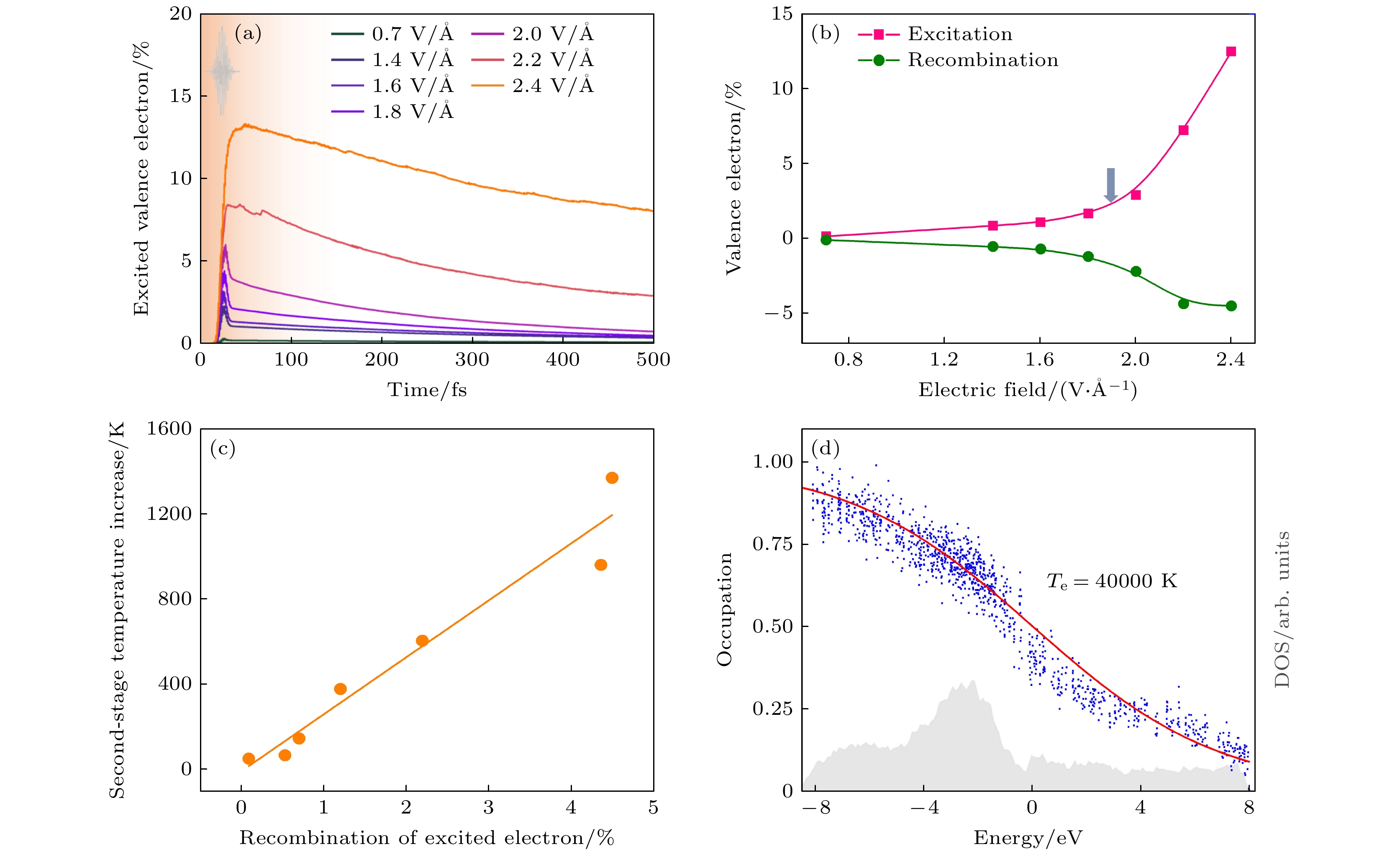
图 27 液态水电子动力学 (a) 受激价电子随激光脉冲电场的时间演化[26]. (b) 激光脉冲电场下的有效电子激发和电子复合. 箭头显示了从多光子到强场电离过程的转变[26]. (c) 电子复合与离子子系统第二阶段升温的关系[26]. (d) 模拟中电场为2.4 V/Å时t = 100 fs时的电子占据, 给出了态的瞬时电子密度[26]
Fig. 27. Electronic dynamics of liquid water. (a) Temporal evolutions of excited valence electrons with the electric field of laser pulses[26]. (b) Effective electron excitation and electron recombination with electric fields of laser pulses. The arrow shows the transition from multiphoton to strong-field ionization processes[26]. (c) Electron recombination vs. the second-stage temperature increase of ionic subsystems[26]. (d) Electronic occupation at t = 100 fs in the simulation with an electric field of 2.4 V/Å. The instantaneous electronic density of states is also shown[26].
表 1 拟合得到的收敛到$ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $阈值的里德伯轨道的能量、宽度以及在X, Y和Z方向的轨道形状示意[32]
Table 1. Energy positions, autoionization widths and views along the X, Y, and Z axes of the Rydberg orbitals for Feshbach resonances converging to the $ \widetilde{{\mathrm{A}}}{}^{2}{{\mathrm{A}}}_{1} $ threshold obtained by fitting[32].
Resonance Energy/eV Widths/meV Diercksen/eV X view Y view Z view 4sa1
5sa1
6sa112.717
13.543
13.91011.33
3.83
1.6312.77
13.67
14.07


3db2 12.886 2.81 13.13 


3da1 12.941 1.41 13.14 


3db1 13.020 2.60 13.25 


4db1
5db113.679
13.9790.90
0.4813.88
14.18


3da1 13.030 2.71 13.23 


4pb2 13.208 3.07 13.35 


4pb1
5pb1
6pb113.297
13.796
14.0393.29
1.36
0.7413.45
13.97
13.97


4pa1
5pa1
6pa113.317
13.804
14.04413.72
6.15
3.2413.51
13.99
14.30


表 2 拟合得到的收敛到$ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $阈值的里德伯轨道的能量、宽度以及在X, Y和Z方向的轨道形状示意[32]
Table 2. Energy positions, autoionization widths and views along the X, Y, and Z axes of the Rydberg orbitals for Feshbach resonances converging to the $ \widetilde{{\mathrm{B}}}{}^{2}{{\mathrm{B}}}_{2} $ threshold obtained by fitting[32].
Resonance Energy/eV Widths/meV Diercksen/eV X view Y view Z view 3pb2 15.888 219.45 15.77 


3pb2 15.888 219.45 15.77 


3pa1 16.212 3.14 15.97 


4sa1 16.885 7.63 16.47 


3db2 17.112 29.38 17.04 


3da2 17.180 2.12 17.03 


4da2
5da217.854
18.1700.88
0.4617.70
18.01


-
[1] van Dishoeck E F, Herbst E, Neufeld D A 2013 Chem. Rev. 113 9043
 Google Scholar
Google Scholar
[2] Zhong J, Kumar M, Anglada J M, Martins-Costa M T C, Ruiz-Lopez M F, Zeng X C, Francisco J S 2019 Annu. Rev. Phys. Chem. 70 45
 Google Scholar
Google Scholar
[3] Bhattacharyya K 2008 Chem. Commun. 25 2848
 Google Scholar
Google Scholar
[4] Laage D, Elsaesser T, Hynes J T 2017 Chem. Rev. 117 10694
 Google Scholar
Google Scholar
[5] Ma R, Cao D, Zhu C, Tian Y, Peng J, Guo J, Chen J, Li X Z, Francisco J S, Zeng X C, Xu L M, Wang E G, Jiang Y 2020 Nature 577 60
 Google Scholar
Google Scholar
[6] Huang X, Wang L, Liu K, Liao L, Sun H, Wang J, Tian X, Xu Z, Wang W, Liu L, Jiang Y, Chen J, Wang E, Bai X 2023 Nature 617 86
 Google Scholar
Google Scholar
[7] Debenedetti P G, Sciortino F, Zerze G H 2020 Science 369 289
 Google Scholar
Google Scholar
[8] Wagstaffe M, Dominguez-Castro A, Wenthaus L, Palutke S, Kutnyakhov D, Heber M, Pressacco F, Dziarzhytski S, Gleissner H, Gupta V K, Redlin H, Dominguez A, Frauenheim T, Rubio A, Stierle A, Noei H 2023 Phys. Rev. Lett. 130 108001
 Google Scholar
Google Scholar
[9] Sudera P, Cyran J D, Deiseroth M, Backus E H G, Bonn M 2020 J. Am. Chem. Soc. 142 12005
 Google Scholar
Google Scholar
[10] Flanagan J C, Valentine M L, Baiz C R 2020 Acc. Chem. Res. 53 1860
 Google Scholar
Google Scholar
[11] Hummer G, Rasaiah J C, Noworyta J P 2001 Nature 414 188
 Google Scholar
Google Scholar
[12] Gallagher K R, Sharp K A 2003 J. Am. Chem. Soc. 125 9853
 Google Scholar
Google Scholar
[13] Tielrooij K J, Garcia-Araez N, Bonn M, Bakker H J 2010 Science 328 1006
 Google Scholar
Google Scholar
[14] Hribar B, Southall N T, Vlachy V, Dill K A 2002 J. Am. Chem. Soc. 124 12302
 Google Scholar
Google Scholar
[15] Gong X, Heck S, Jelovina D, Perry C, Zinchenko K, Lucchese R, Worner H J 2022 Nature 609 507
 Google Scholar
Google Scholar
[16] Huppert M, Jordan I, Baykusheva D, von Conta A, Worner H J 2016 Phys. Rev. Lett. 117 093001
 Google Scholar
Google Scholar
[17] Herbert J M, Coons M P 2017 Annu. Rev. Phys. Chem. 68 447
 Google Scholar
Google Scholar
[18] Savolainen J, Uhlig F, Ahmed S, Hamm P, Jungwirth P 2014 Nat. Chem. 6 697
 Google Scholar
Google Scholar
[19] Ghalgaoui A, Koll L M, Schutte B, Fingerhut B P, Reimann K, Woerner M, Elsaesser T 2020 J. Phys. Chem. Lett. 11 7717
 Google Scholar
Google Scholar
[20] Zhang Z, Piatkowski L, Bakker H J, Bonn M 2011 J. Chem. Phys. 135 021101
 Google Scholar
Google Scholar
[21] Sudera P, Cyran J D, Bonn M, Backus E H G 2021 J. Phys. Chem. C 125 22937
 Google Scholar
Google Scholar
[22] Venkatraman R K, Baiz C R 2020 Langmuir 36 6502
 Google Scholar
Google Scholar
[23] Chen Z, Na X, Curry C B, Liang S, French M, Descamps A, DePonte D P, Koralek J D, Kim J B, Lebovitz S, Nakatsutsumi M, Ofori-Okai B K, Redmer R, Roedel C, Schörner M, Skruszewicz S, Sperling P, Toleikis S, Mo M Z, Glenzer S H 2021 Matter Radiat. Extremes 6 054401
 Google Scholar
Google Scholar
[24] Lu L, Wildman A, Jenkins A J, Young L, Clark A E, Li X 2020 J. Phys. Chem. Lett. 11 9946
 Google Scholar
Google Scholar
[25] Lan J, Kapil V, Gasparotto P, Ceriotti M, Iannuzzi M, Rybkin V V 2021 Nat. Commun. 12 766
 Google Scholar
Google Scholar
[26] Xu J, Chen D, Meng S 2021 J. Am. Chem. Soc. 143 10382
 Google Scholar
Google Scholar
[27] Seideman T 2002 Annu. Rev. Phys. Chem. 53 41
 Google Scholar
Google Scholar
[28] Pazourek R, Nagele S, Burgdörfer J 2015 Rev. Mod. Phys. 87 765
 Google Scholar
Google Scholar
[29] Committee P S 1986 Atomic, Molecular, and Optical Physics: Panel on Atomic, Molecular, and Optical Physics (Washington, D. C. : National academy press
[30] Schoun S B, Chirla R, Wheeler J, Roedig C, Agostini P, DiMauro L F, Schafer K J, Gaarde M B 2014 Phys. Rev. Lett. 112 153001
 Google Scholar
Google Scholar
[31] Borras V J, Gonzalez-Vazquez J, Argenti L, Martin F 2021 J. Chem. Theory Comput. 17 6330
 Google Scholar
Google Scholar
[32] Fernandez-Milan P, Borras V J, Gonzalez-Vazquez J, Martin F 2023 J. Chem. Phys. 158 134305
 Google Scholar
Google Scholar
[33] Alizadeh E, Orlando T M, Sanche L 2015 Annu. Rev. Phys. Chem. 66 379
 Google Scholar
Google Scholar
[34] Wilhelm J, VandeVondele J, Rybkin V V 2019 Angew. Chem. Int. Ed. 58 3890
 Google Scholar
Google Scholar
[35] Pizzochero M, Ambrosio F, Pasquarello A 2019 Chem. Sci. 10 7442
 Google Scholar
Google Scholar
[36] Loh Z H, Doumy G, Arnold C, Kjellsson L, Southworth S, Al Haddad A, Kumagai Y, Tu M F, Ho P, March A 2020 Science 367 179
 Google Scholar
Google Scholar
[37] Shepard C, Kanai Y 2022 Phys. Chem. Chem. Phys. 24 5598
 Google Scholar
Google Scholar
[38] Marsalek O, Elles C G, Pieniazek P A, Pluharova E, VandeVondele J, Bradforth S E, Jungwirth P 2011 J. Chem. Phys. 135 224510
 Google Scholar
Google Scholar
[39] Zhao R, You P, Meng S 2023 Phys. Rev. Lett. 130 166401
 Google Scholar
Google Scholar
[40] Jones L O, Schatz G C 2023 J. Phys. Chem. Lett. 14 3521
 Google Scholar
Google Scholar
[41] Schaffer C B, Nishimura N, Glezer E N, Kim A M-T, Mazur E 2002 Opt. Express 10 196
 Google Scholar
Google Scholar
[42] Klein A L, Bouwhuis W, Visser C W, Lhuissier H, Sun C, Snoeijer J H, Villermaux E, Lohse D, Gelderblom H 2015 Phys. Rev. Appl. 3 044018
 Google Scholar
Google Scholar
[43] Stan C A, Milathianaki D, Laksmono H, Sierra R G, McQueen Trevor A, Messerschmidt M, Williams G J, Koglin J E, Lane T J, Hayes Matt J, Guillet S A H, Liang M, Aquila A L, Willmott P R, Robinson Joseph S, Gumerlock K L, Botha S, Nass K, Schlichting I, Shoeman Robert L, Stone H A, Boutet S 2016 Nat. Phys. 12 966
 Google Scholar
Google Scholar
[44] Beyerlein K R, Jönsson H O, Alonso-Mori R, Aquila A, Bajt S, Barty A, Bean R, Koglin J E, Messerschmidt M, Ragazzon D 2018 Proc. Natl. Acad. Sci. U. S. A. 115 5652
 Google Scholar
Google Scholar
[45] Medvedev N, Voronkov R, Volkov A E 2023 J. Chem. Phys. 158 074501
 Google Scholar
Google Scholar
计量
- 文章访问数: 4810
- PDF下载量: 198
- 被引次数: 0














 下载:
下载: