-
Rydberg atoms are important building blocks for quantum technologies, exploited to new applications in quantum computing, quantum communication and quantum sensing due to their unique tunable quantum properties.Besides the widely-used few-photon resonant excitation for the specific Rydberg state, multiple Rydberg states can be populated coherently and efficiently through the frustrated tunneling ionization or the Coulomb potential recapture effect in strong laser field. The Rydberg states excitation in strong field provides an opportunity to realize the ultrafast quantum control on Rydberg atom and bridge the strong field physics and quantum information technology.Using the Classical Trajectory Monte Carlo method and Qprop package to solve Time-Dependent Schrödinger Equation, we calculate the population of Rydberg states. Our results show that the population increases with the parameter of the asymmetric laser envelope. Based on the Quantitative Rescattering theory, the calculated time-dependence of recapture rate is negatively related to the laser envelope and the residual laser interaction time, which is termed as envelope effect. Combined with the carrier-wave effect, an analytic formula is proposed to calculate the Rydberg states population:$ Y(t) \propto $$ W_0\left(t\right) \dfrac{t-\tau+c}{f\left(t\right)} \cos \left(\omega t+\phi\right) . $ This results open the door to enhance the Rydberg states generation using the laser envelope control, benefiting the future quantum technology based on the Rydberg states generated in the strong laser field.
-
Keywords:
- Rydberg states /
- Strong field excitation /
- Ultrafast dynamics
-
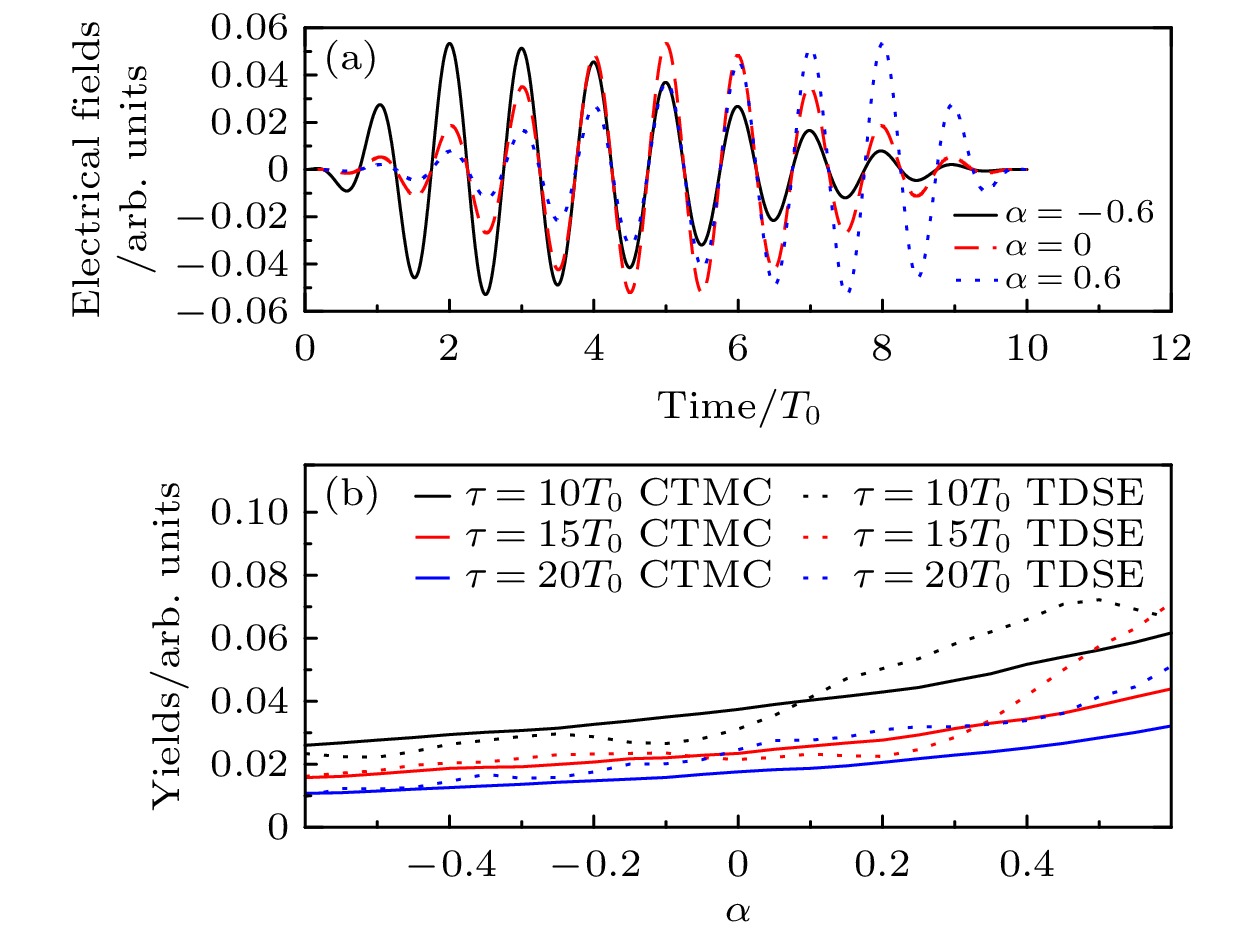
图 1 里德堡态产额随激光脉冲参数的变化. (a)具有相同脉冲持续时间$ \tau=10 T_0 $和不同不对称参数α的激光电场. 黑色实线, 红色虚线, 蓝色点线分别为$ \alpha=-0.6, 0, 0.6 $. (b)在不同激光脉冲持续时间下, 里德堡态的产率随不对称参数的变化而变化. 黑、红、蓝线分别为$ \tau=10 T_0, 15 T_0, $$ 20 T_0 $, 实线和点线分别为CTMC和TDSE计算的里德堡态激发的产率. 当α从–0.6增加到0.6时, 里德堡态的产率约增加一倍, 表明在上升沿较长的激光脉冲中更有可能产生里德堡态
Fig. 1. Rydberg state yield variation with laser pulse parameters. (a) Laser electric fields with the same pulse duration $ \tau=10 T_0 $ and different asymmetric parameters α. Black solid line, red dashed line and blue dotted line are for $ \alpha=-0.6, 0, 0.6 $ respectively. (b) The yields of Rydberg states change with the asymmetric parameter under different laser pulse duration. Black, red and blue line are for $ \tau=10 T_0, 15 T_0, 20 T_0 $ while solid line and dotted line are for RSE yields calculated using CTMC and TDSE respectively. The yields of the Rydberg states approximately double when α increases from -0.6 to 0.6, indicating the Rydberg states are more possible to be generated in the laser pulse with longer rising edge.
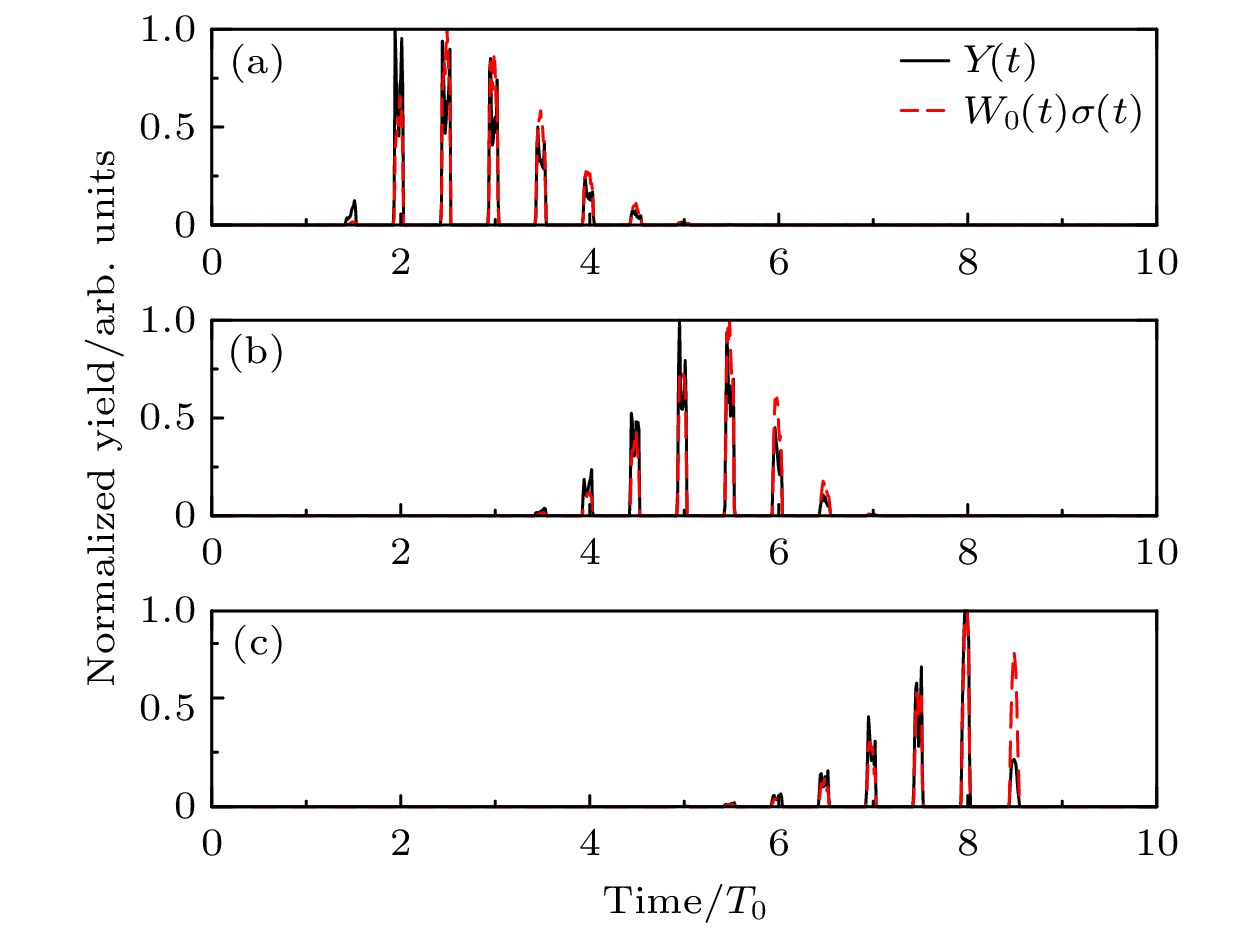
图 2 里德堡态的时间依赖性. 在相同脉冲持续时间$ \tau=10 T_0 $下, 不对称参数$ \alpha=-0.6, 0, 0.6 $时的$ Y(t) $(黑色实线)和$ W_0(t)\sigma(t) $(红色虚线). 里德堡态主要是由电子在每个半周期的场峰附近隧穿产生的, 称为“载波效应”. 对于不同的α, 主导周期随包络线的不对称性而变化, 这可称为“包络效应”
Fig. 2. The time dependence of the Rydberg states yields. The time dependence of the Rydberg states yields Y(t) (black solid line) and $ W_0(t)\sigma(t) $ (red dashed line) with the same pulse duration $ \tau=10 T_0 $ and the asymmetric parameters $ \alpha=-0.6, 0, 0.6 $. The Rydberg states are mainly generated from electrons tunneling near the field peak of each half-cycle termed as “carrier-wave effect”. For different α, the dominating cycles change with the asymmetry of the envelope, which can be termed as “envelope effect”.
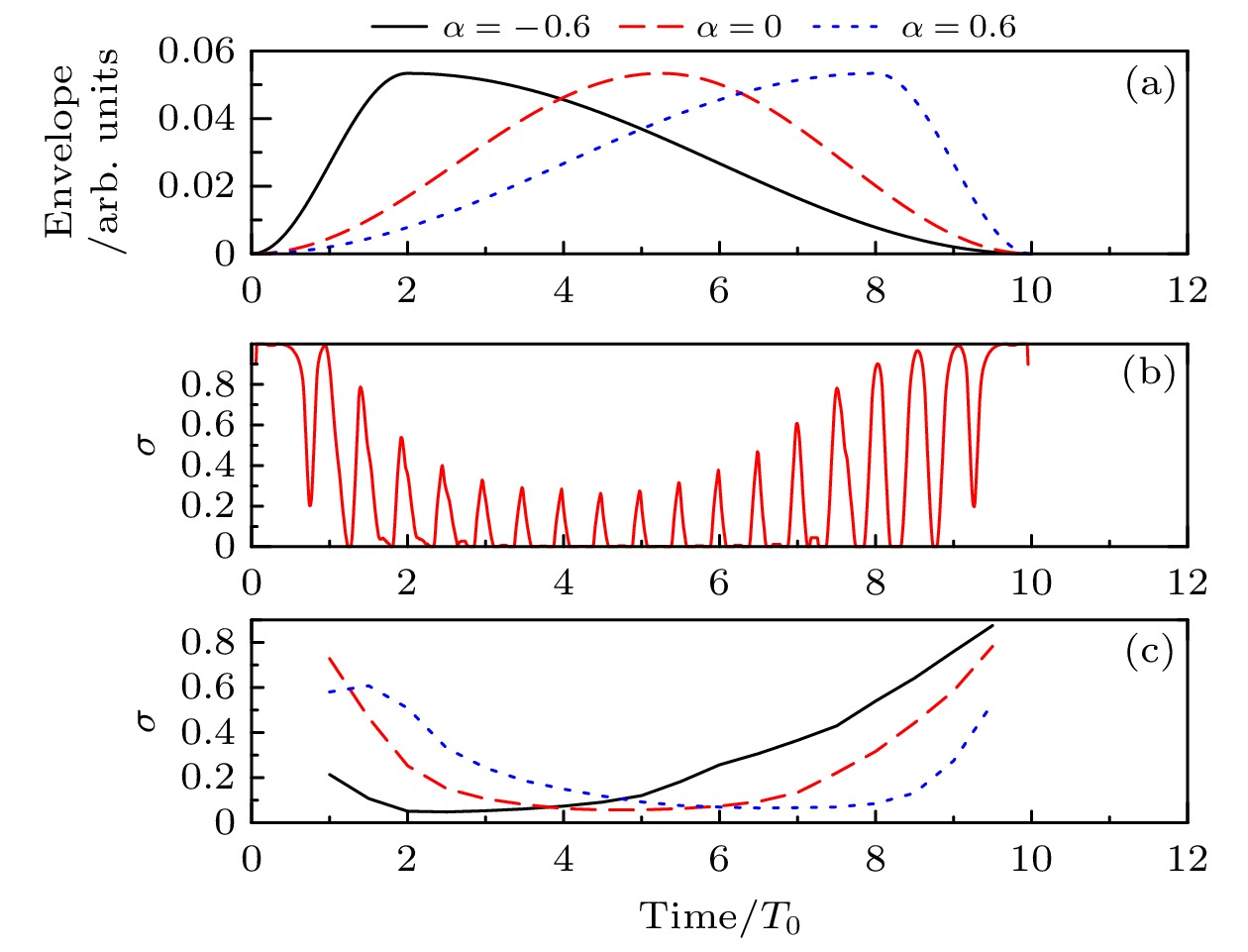
图 3 不对称包络下的时间依赖性. (a)不同不对称参数下的激光脉冲包络线. (b)激光包络对称$ \alpha=0 $时再捕获率的时间依赖性. (c)不同不对称参数下每半周期平均总再捕获率的时间依赖性. 在(a)和(c)中, 黑色实线、红色虚线和蓝色点线分别表示$ \alpha=-0.6, 0, 0.6 $. 对于不同的不对称参数, 再捕获率与包络线均呈现负相关关系, 使得再捕获率在隧穿电离的主导周期内达到最小
Fig. 3. The time dependence of the recapture rate with asymmetric laser pulse envelopes. (a) Laser pulse envelopes with different asymmetric parameters. (b) The time dependence of the recapture rate with symmetric laser envelope $ \alpha=0 $. (c) The time dependence of the total recapture rate averaged in every half-cycle with different asymmetric parameters. Black solid line, red dashed line and blue dotted line are for $ \alpha=-0.6, 0, 0.6 $ respectively in (a) and (c). The negative relation between recapture rate and the envelope is universal for different asymmetric parameters, making the recapture rate attain minimization in the dominating cycles of tunneling ionization.
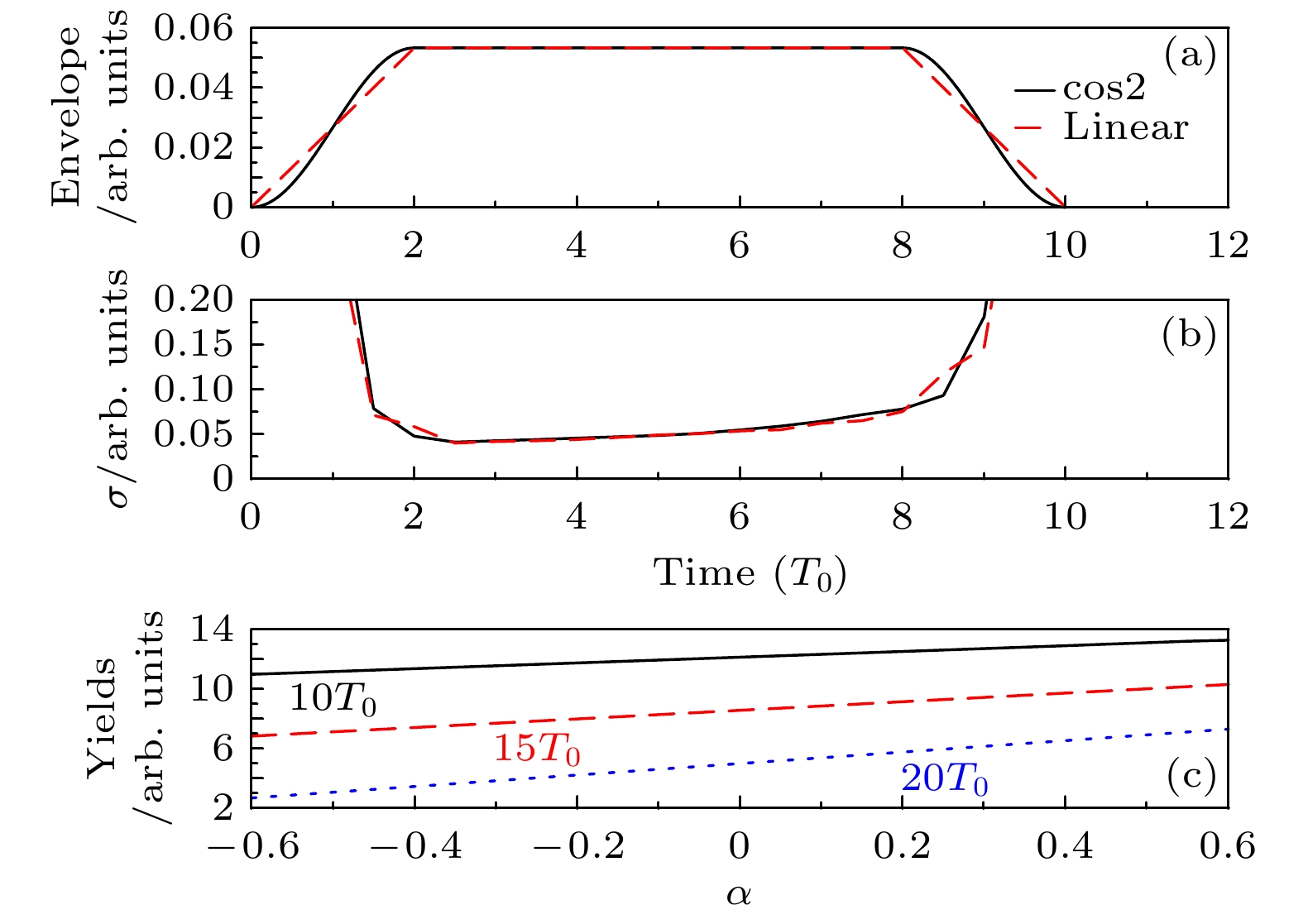
图 4 梯形激光脉冲包络线下的时间依赖性. (a)具有余弦平方和线性边缘的梯形激光脉冲包络. (b)梯形激光脉冲包络每半周期总再捕获率的时间依赖性. 当残余激光相互作用时间超过特定标准时, 电子轨迹从再捕获转变为弹性散射. (c)在与图1相同的激光参数下, 利用公式(10)得到的里德堡态的产率, 其中随α的增加与利用CTMC和TDSE计算得到的布居吻合得很好
Fig. 4. The time dependence of the recapture rate with trapezoidal laser pulse envelopes. (a) Trapezoidal laser pulse envelopes with cosine square and linear edges. (b) The time dependence of the total recapture rate in every half-cycle with trapezoidal laser pulse envelopes. The increase can be due to the change of the electron's trajectory from recapture to elastic recollision when the residual laser interaction time exceed a specific criterion. (c) The yield of the Rydberg states using Eq.10 under the same laser parameters with Fig. 1, where the increase with α agrees well with the calculated population using CTMC and TDSE.
-
[1] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[2] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[3] Adams C S, Pritchard J D, Shaffer J P 2020 J. Phys. B: At. Mol. Opt. Phys. 53 012002
Google Scholar
[4] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110
Google Scholar
[5] Pan L, Zhai H 2022 Phys. Rev. Res. 4 L032037
Google Scholar
[6] Jaksch D, Cirac J I, Zoller P, Rolston S L, Côté R, Lukin M D 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[7] Baur S, Tiarks D, Rempe G, Dürr S 2014 Phys. Rev. Lett. 112 073901
Google Scholar
[8] Vassen W, Cohen-Tannoudji C, Leduc M, Boiron D, Westbrook C I, Truscott A, Baldwin K, Birkl G, Cancio P, Trippenbach M 2012 Rev. Mod. Phys. 84 175
Google Scholar
[9] Saffman M, Walker T G 2002 Phys. Rev. A 66 065403
Google Scholar
[10] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[11] Schafer K J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599
Google Scholar
[12] Becker W, Liu X J, Ho P J, Eberly J H 2012 Rev. Mod. Phys 84 1011
Google Scholar
[13] Shen X C, Liu Y, Chen Q, Lü H, Xu H F 2022 Acta Phys. Sin. 71 233202
Google Scholar
[14] Freeman R R, Bucksbaum P H, Milchberg H, Darack S, Schumacher D, Geusic M E 1987 Phys. Rev. Lett. 59 1092
Google Scholar
[15] De Boer M P, Muller H G 1992 Phys. Rev. Lett. 68 2747
Google Scholar
[16] Wang B B, Li X F, Fu P M, Chen J, Liu J 2006 Chin. Phys. Lett. 23 2729
Google Scholar
[17] Nubbemeyer T, Gorling K, Saenz A, Eichmann U, Sandner W 2008 Phys. Rev. Lett. 101 233001
Google Scholar
[18] Eichmann U, Saenz A, Eilzer S, Nubbemeyer T, Sandner W 2013 Phys. Rev. Lett. 110 203002
Google Scholar
[19] Li Q G, Tong X M, Morishita T, Wei H, Lin C D 2014 Phys. Rev. A 89 023421
Google Scholar
[20] Ortmann L, Hofmann C, Landsman A S 2018 Phys. Rev. A 98 033415
Google Scholar
[21] Liu M Q, Xu S P, Hu S L, Becker W, Quan W, Liu X J, Chen J 2021 Optica 8 765
Google Scholar
[22] Ortmann L, Hofmann C, Ivanov I A, Landsman A S 2021 Phys. Rev. A 103 063112
Google Scholar
[23] Zhao J, Liu J L, Wang X W, Zhao Z X 2024 Chin. Phys. Lett. 41 013201
Google Scholar
[24] Liu J L, Zhao J, Huang Y D, Wang X W, Zhao Z X 2020 Phys. Rev. A 102 023109
Google Scholar
[25] Chetty D, Glover R D, Tong X M, deHarak B A, Xu H, Haram N, Bartschat K, Palmer A J, Luiten A N, Light P S, Litvinyuk I V, Sang R T 2022 Phys. Rev. Lett. 128 173201
Google Scholar
[26] Larimian S, Lemell C, Stummer V, Geng J W, Roither S, Kartashov D, Zhang L, Wang M X, Gong Q H, Peng L Y 2017 Phys. Rev. A 96 021403
Google Scholar
[27] Venzke J, Gebre Y, Becker A, Jaroń-Becker A 2020 Phys. Rev. A 101 053425
Google Scholar
[28] Solanpää J, Räsänen E 2018 Phys. Rev. A 98 053422
Google Scholar
[29] Zhang B, Chen W B, Zhao Z X 2014 Phys. Rev. A 90 023409
Google Scholar
[30] Zhao X Y, Wang C C, Hu S L, Li W D, Chen J, Hao X L 2019 Chin. Phys. B 28 083202
Google Scholar
[31] Toyota K, Saalmann U, Rost J M 2015 New J. Phys. 17 073005
Google Scholar
[32] Ning Q C, Saalmann U, Rost J M 2018 Phys. Rev. Lett. 120 033203
Google Scholar
[33] Leemans W P, Catravas P, Esarey E, Geddes C, Toth C, Trines R, Schroeder C B, Shadwick B A, Van-Tilborg J, Faure J 2002 Phys. Rev. Lett. 89 174802
Google Scholar
[34] Tulsky V, Bauer D 2020 Comput. Phys. Commun. 251 107098
Google Scholar
[35] Ammosov M V, Delone N B, Krainov V P 1986 J. Exp. Theor. Phys. 64 1191
[36] Delone N B, Krainov V P 1991 J. Opt. Soc. Am. B 8 1207
[37] Liu J L, Chen W B, Zhang B, Zhao J, Wu J H, Yuan J M, Zhao Z X 2014 Phys. Rev. A 90 063420
Google Scholar
[38] Becker R L, MacKellar A D 1984 J. Phys. B:At. Mol. Opt. Phys. 17 3923
Google Scholar
[39] Emmanouilidou A, Lazarou C, Staudte A, Eichmann U 2012 Phys. Rev. A 85 011402
Google Scholar
[40] Shvetsov-Shilovski N I, Goreslavski S P, Popruzhenko S V, Becker W 2009 Laser Phys. 19 1550
Google Scholar
[41] Le A T, Lucchese R R, Tonzani S, Morishita T, Lin C D 2009 Phys. Rev. A 80 013401
Google Scholar
[42] Chetty D, Glover R D, deHarak B A, Tong X M, Xu H, Pauly T, Smith N, Hamilton K R, Bartschat K, Ziegel J P, Douguet N, Luiten A N, Light P S, Litvinyuk I, Sang R 2020 Phys. Rev. A 101 053402
Google Scholar
[43] Bengs U, Patchkovskii S, Ivanov M, Zhavoronkov N 2022 Phys. Rev. Res. 4 023135
Google Scholar
下载:
计量
- 文章访问数: 180
- PDF下载量: 3
- 被引次数: 0
