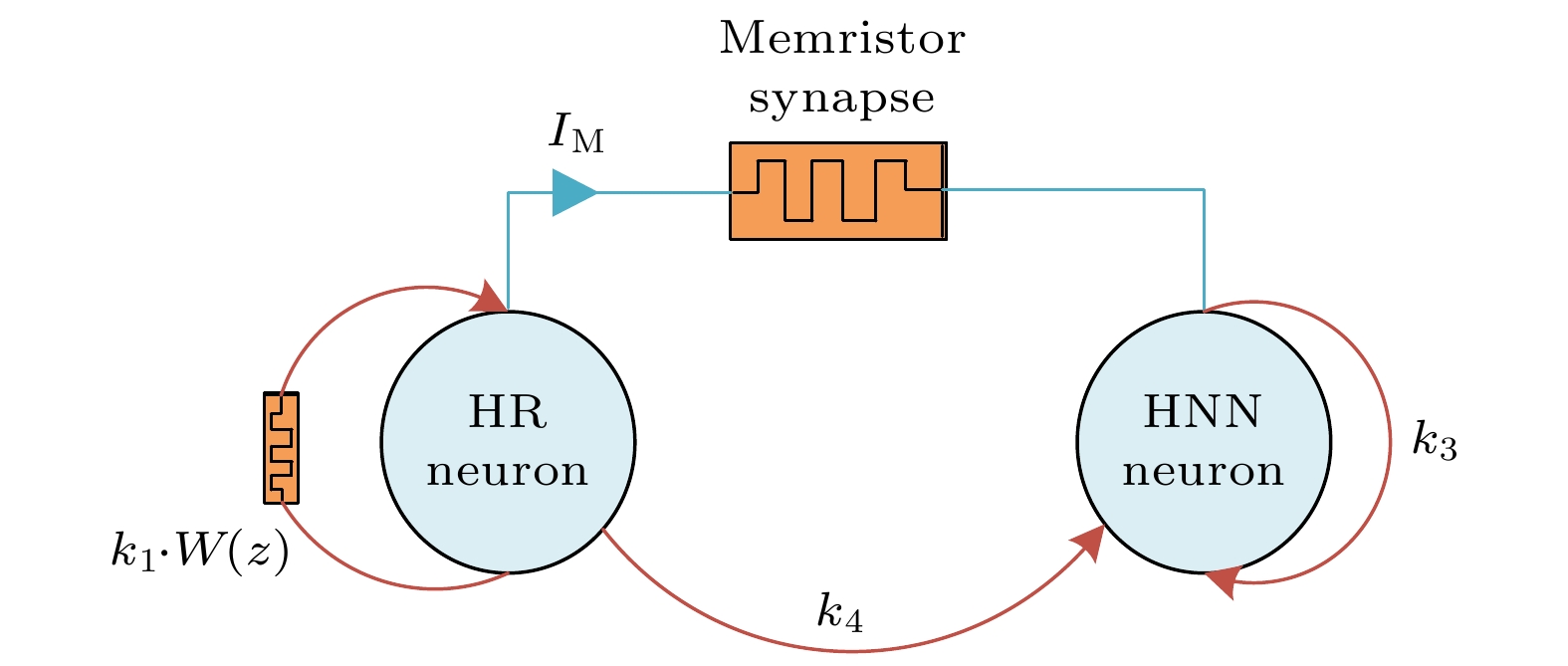
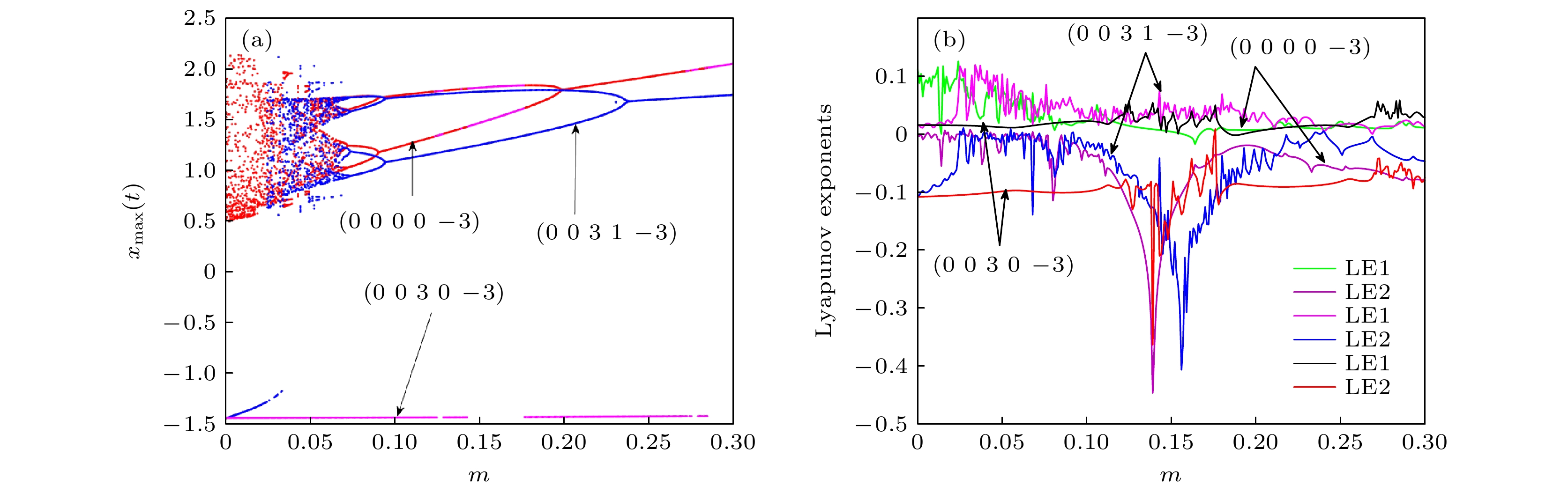
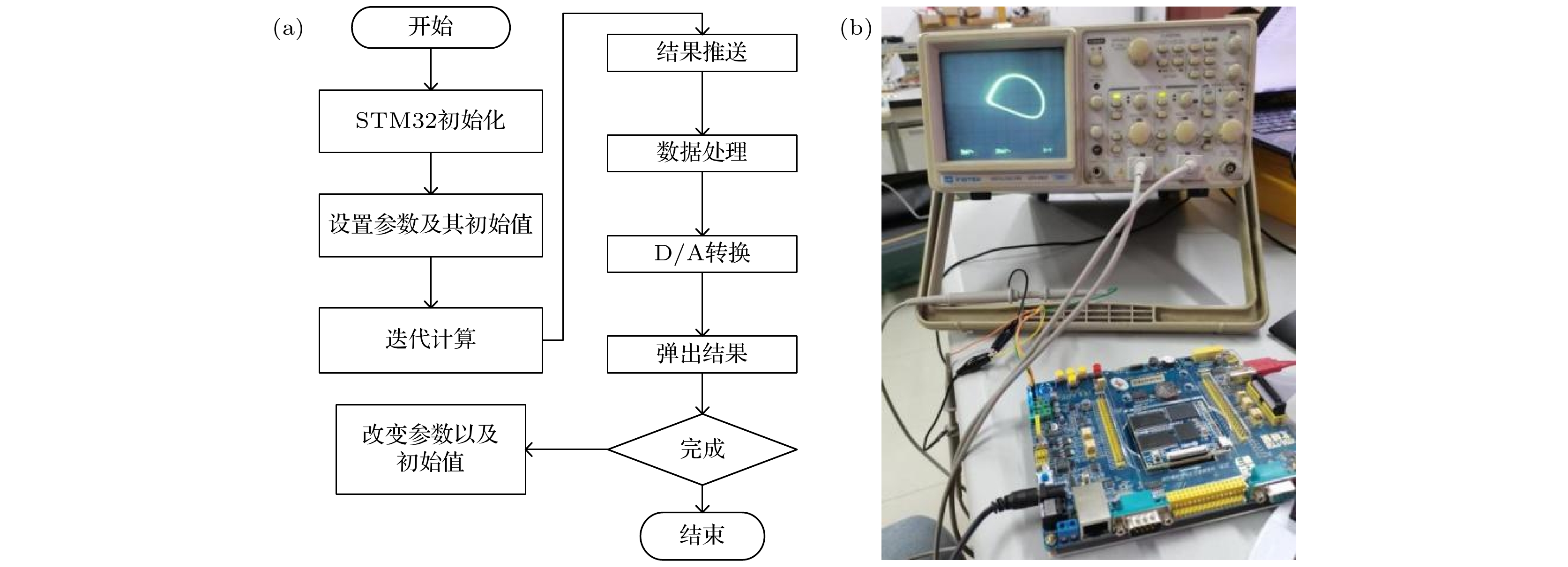
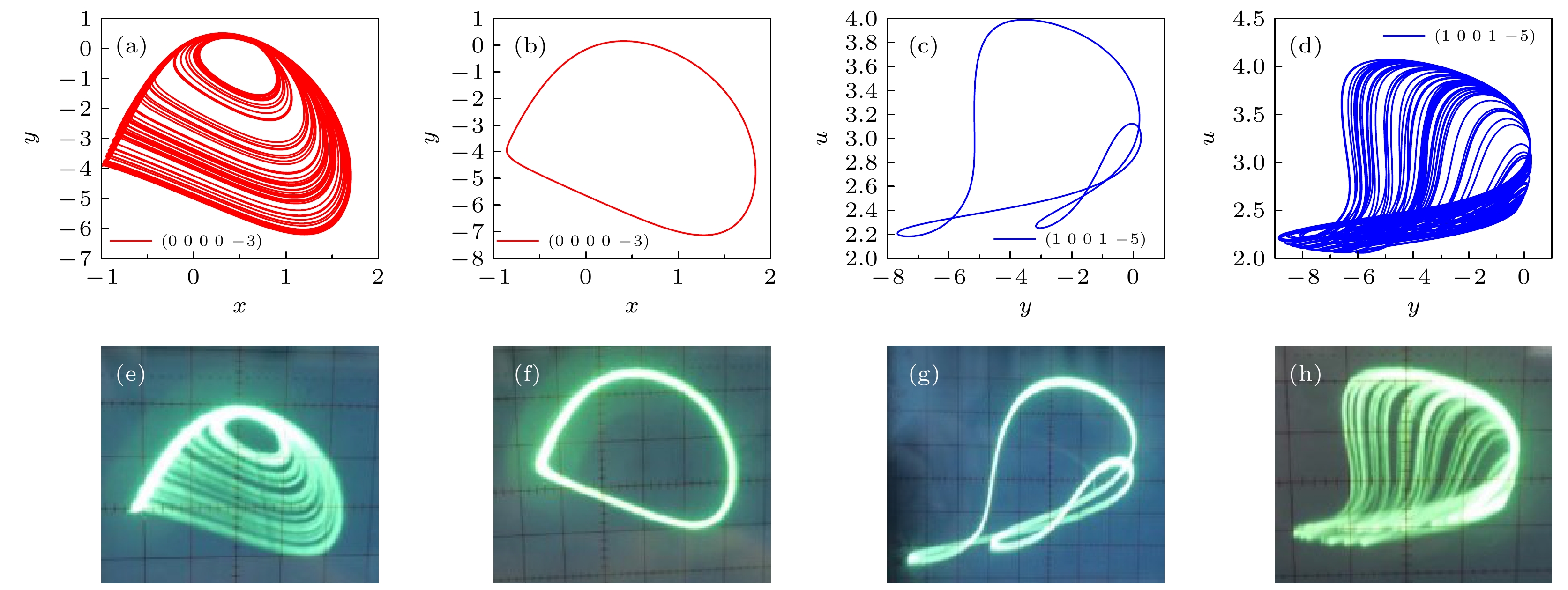
-
不同的神经元之间具有异质性, 神经元活动具有很大的差异, 因此研究异质神经元之间的耦合越来越受到关注. 本文将Hindmarsh-Rose神经元模型和Hopfield神经元模型经过忆阻电磁感应耦合, 构成一个新的神经元模型. 利用相图、分岔图、李雅普诺夫指数图和吸引盆, 证明对于耦合强度和其他参数, 新的神经元模型表现出不同吸引子共存现象. 在保持相关参数不变时, 通过改变初始状态, 可以观察到系统的多稳态现象, 包括不同周期的共存, 周期与混沌现象的共存等. 最后基于高级RISC机 (advanced RISC machine, ARM)的微控制单元 (micro control unit, MCU)实现了该神经元模型, 实验结果表明理论分析的有效性.There is heterogeneity among different neurons, and the activities of neurons are greatly different, so the coupling between heterogeneous neurons can show richer dynamic phenomena, which is of great significance in understanding the neural function of the human brain. Unfortunately, in many studies of memristive coupled neurons, researchers have considered two adjacent identical neurons, but ignored the heterogeneous neurons. In this paper, two models are chosen, i.e. a Hindmarsh-Rose neuron model and a Hopfield neuron model, which are very different from each other. The proposed fractional-order linear memristor and fractional-order hyperbolic memristor simulated neural synapses are introduced into the two heterogeneous neuron models, considering not only the coupling between the two neurons, but also the coupling between single neurons. The self-coupling of neurons, a five-dimensional fractional memristive coupled heterogeneous neuron model, is established. In the numerical simulation of the new neuron model, the phase diagrams, bifurcation diagrams, Lyapunov exponent diagrams, and attraction basins are used to demonstrate the changes in coupling strength and other parameters in the memristive coupled heterogeneous neuron model, the new neuron model performance coexistence of different attractors. On the other hand, by changing the initial state of the system while keeping the relevant parameters of the system unchanged, the multistable phenomenon of the coupled heterogeneous neuron model can be observed. Using the phase diagram, the coexistence of different periods, and the phenomenon of period and chaos can be clearly observed. The coexistence of different attractor states can also be observed in the attractor basin. This has many potential implications for studying dynamic memory and information processing in neurons. Uncovering different types of multistable states from a dynamical perspective can provide an insight into the role of multistable states in brain information processing and cognitive function. Finally, the neuron model is implemented based on the micro control unit of the advanced RISC machine, and the phase diagram is observed under some parameters of the coupled neuron model on an oscilloscope. The experimental results show the validity of the theoretical analysis.
-
Keywords:
- heterogeneous neurons /
- memristive /
- attractors coexistence /
- multistable
[1] 孙军伟, 杨建领, 刘鹏, 王延峰 2022 电子与信息学报 44 1
Google Scholar
Sun J W, Yang J L, Liu P, Wang Y F 2022 J. Electron. Inf. Technol. 44 1
Google Scholar
[2] Yang N N, Xu C, Wu C J, Jia R, Lin C X 2018 Complexity 9467435 1
Google Scholar
[3] 邵楠, 张盛兵, 邵舒渊 2016 65 128503
Google Scholar
Shao N, Zhang S B, Shao S Y 2016 Acta Phys. Sin. 65 128503
Google Scholar
[4] 罗佳, 孙亮, 乔印虎 2022 计算物理 39 109
Google Scholar
Luo J, Sun L, Qiao Y H 2022 Chin. J. Comput. Phys. 39 109
Google Scholar
[5] 周小荣, 罗晓曙, 蒋品群, 袁五届 2007 56 5679
Google Scholar
Zhou X R, Luo X S, Jing P Q, Yuan W J 2007 Acta Phys. Sin. 56 5679
Google Scholar
[6] Jin J, Zhao L, Li M, Yu F, Xi Z 2020 Neural Comput. 32 4151
Google Scholar
[7] 王宝燕, 徐伟, 邢真慈 2009 58 6590
Google Scholar
Wang B Y, Xu W, Xing Z C 2009 Acta Phys. Sin. 58 6590
Google Scholar
[8] Xu Y, Jia Y, Ge M Y, Lu L L, Yang L J, Zhan X 2018 Neurocomputing. 283 196
Google Scholar
[9] Bao B C, Yang Q, Zhu L, Bao H 2019 Int. J. Bifurc. Chaos 29 10
Google Scholar
[10] Chen C, Chen J, Bao H, Chen M, Bao B 2019 Nonlinear Dyn. 95 3385
Google Scholar
[11] Bao H, Hu A, Liu W, Bao B 2020 IEEE Trans. Neural Netw. Learn. Syst. 31 502
Google Scholar
[12] 丁学利, 古华光, 贾冰, 李玉叶 2021 70 218701
Google Scholar
Ding X L, Gu H G, Jia B, Li Y Y 2021 Acta Phys. Sin. 70 218701
Google Scholar
[13] 吴莹, 徐健学, 何岱海, 靳伍银 2005 54 3457
Google Scholar
Wu Y, Xu J X, He D H, Jin W Y 2005 Acta Phys. Sin. 54 3457
Google Scholar
[14] Wang Q Y, Zhang H H, Chen G R 2012 Chaos 22 1
Google Scholar
[15] Han F, Wang Z 2015 Int. J. Nonlin. Mech. 70 105
Google Scholar
[16] Cheng L, Cao H 2017 Int. J. Bifurcat. Chaos 27 1
Google Scholar
[17] 孙晓娟, 杨白桦, 吴晔, 肖井华 2014 63 120502
Google Scholar
Sun X J, Yang B H, Wu Y, Xiao J H 2014 Acta Phys. Sin. 63 120502
Google Scholar
[18] Bao H, Zhang Y, Liu W 2020 Nonlinear Dyn. 100 937
Google Scholar
[19] Bao H, Liu W, Hu A 2019 Nonlinear Dyn. 95 43
Google Scholar
[20] Cang S, Li Y, Zhang R, Wang, Z 2019 Nonlinear Dyn. 95 381
Google Scholar
[21] Zhang X, Wang C, Yao W, Lin H 2019 Nonlinear Dyn. 97 2159
Google Scholar
[22] 张学丰, 彭良玉, 彭代鑫 2022 电子元件与材料 41 315
Google Scholar
Zhang X F, Peng D X 2022 Electron. Compon. Mater. 41 315
Google Scholar
[23] 包涵, 包伯成, 林毅, 王将, 武花干 2016 65 180501
Google Scholar
Bao H, Bao B C, Lin Y, Wang J, Wu H G 2016 Acta Phys. Sin. 65 180501
Google Scholar
[24] 谢盈, 朱志刚, 张晓锋, 任国栋 2021 70 210502
Google Scholar
Xie Y, Zhu Z G, Zhang X F, Ren G D 2021 Acta Phys. Sin. 70 210502
Google Scholar
[25] Parastesh F, Jafari S, Azarnoush H 2019 Eur. Phys. J. Spec. Top. 228 2123
Google Scholar
[26] Caputo M 1966 Ann. Geophys. 19 529
Google Scholar
-
图 1 分数阶忆阻器的磁滞回线 (a)
$ F = 1 $ , 不同的振幅; (b)$ A = 4 $ , 不同频率Fig. 1. Hysteresis loop of fractional-order memristor: (a) Different amplitudes for
$ F = 1 $ ; (b) different frequencies for$ A = 4 $ .
图 3 关于耦合系数m的共存现象 (a)关于m的分岔图; (b)对应前两个
$ {\text{Lyapunov}} $ 指数图Fig. 3. Coexistence of coupling coefficients: (a) Bifurcation diagram of the relationship; (b) corresponding to the first two exponential diagrams.
图 4 确定值
$ m $ , x-y平面上的相图 (a)$ m = 0.015 $ ; (b)$ m = 0.05 $ ; (c)$ m = 0.215 $ ; (d)$ m = 0.26 $ Fig. 4. Determination of values, phase diagrams on the x-y plane: (a)
$ m = 0.015 $ ; (b)$ m = 0.05 $ ; (c)$ m = 0.215 $ ; (d)$ m = 0.26 $ .
图 5
$ {k_1} $ 取不同值时$z(0{\text{)-}}u{\text{(0)}}$ 初始平面的局部吸引盆 (a)$ {k_1} = 1.5 $ ; (b)$ {k_1} = 1.8 $ Fig. 5. Local attraction basin of the
$z(0{\text{)-}}u{\text{(0)}}$ initial plane with different values: (a)$ {k_1} = 1.5 $ ; (b)$ {k_1} = 1.8 $ .
图 6
$ {k_1} $ 取不同值时, y-u平面的吸引子共存现象 (a)$ {k_1} = 1.5 $ ; (b)$ {k_1} = 1.8 $ Fig. 6. Coexistence of y-u plane attractors with different values: (a)
$ {k_1} = 1.5 $ ; (b)$ {k_1} = 1.8 $ .
图 7 (a) STM32实现的编程流程; (b) STM32实现的实验平台
Fig. 7. (a) STM32 realized programming flow; (b) STM32 realized experimental platform.
图 8 部分参数的 MATLAB仿真图和单片机实验结果 (a)—(d) MATLAB仿真图; (e)—(h)单片机实验结果
Fig. 8. Simulation diagram of some parameters and experimental results of MCU microcomputer: (a)–(d) Simulation diagram; (e)–(h) experimental results of single-chip microcomputer.
表 1 耦合神经元的特征值
Table 1. Eigenvalues of coupled neurons.
$ {\lambda _1} $ $ {\lambda _2} $ $ {\lambda _3} $ $ {\lambda _4} $ $ {\lambda _5} $ $ {\sigma _1} > 0,{\sigma _2} > 0,{\sigma _3} > 0 $ 0 1 正实根 正实根 正实根 $ {\sigma _1} > 0,{\sigma _2} > 0,{\sigma _3} < 0 $ 0 1 正实根 正实根 负实根 $ {\sigma _1} > 0,{\sigma _2} < 0,{\sigma _3} > 0 $ 0 1 正实根 负实根 正实根 $ {\sigma _1} > 0,{\sigma _2} < 0,{\sigma _3} < 0 $ 0 1 正实根 负实根 负实根 $ {\sigma _1} < 0,{\sigma _2} > 0,{\sigma _3} > 0 $ 0 1 负实根 正实根 正实根 $ {\sigma _1} < 0,{\sigma _2} > 0,{\sigma _3} < 0 $ 0 1 负实根 正实根 负实根 $ {\sigma _1} < 0,{\sigma _2} < 0,{\sigma _3} > 0 $ 0 1 负实根 负实根 正实根 $ {\sigma _1} < 0,{\sigma _2} < 0,{\sigma _3} < 0 $ 0 1 负实根 负实根 负实根 
下载: 导出CSV
-
[1] 孙军伟, 杨建领, 刘鹏, 王延峰 2022 电子与信息学报 44 1
Google Scholar
Sun J W, Yang J L, Liu P, Wang Y F 2022 J. Electron. Inf. Technol. 44 1
Google Scholar
[2] Yang N N, Xu C, Wu C J, Jia R, Lin C X 2018 Complexity 9467435 1
Google Scholar
[3] 邵楠, 张盛兵, 邵舒渊 2016 65 128503
Google Scholar
Shao N, Zhang S B, Shao S Y 2016 Acta Phys. Sin. 65 128503
Google Scholar
[4] 罗佳, 孙亮, 乔印虎 2022 计算物理 39 109
Google Scholar
Luo J, Sun L, Qiao Y H 2022 Chin. J. Comput. Phys. 39 109
Google Scholar
[5] 周小荣, 罗晓曙, 蒋品群, 袁五届 2007 56 5679
Google Scholar
Zhou X R, Luo X S, Jing P Q, Yuan W J 2007 Acta Phys. Sin. 56 5679
Google Scholar
[6] Jin J, Zhao L, Li M, Yu F, Xi Z 2020 Neural Comput. 32 4151
Google Scholar
[7] 王宝燕, 徐伟, 邢真慈 2009 58 6590
Google Scholar
Wang B Y, Xu W, Xing Z C 2009 Acta Phys. Sin. 58 6590
Google Scholar
[8] Xu Y, Jia Y, Ge M Y, Lu L L, Yang L J, Zhan X 2018 Neurocomputing. 283 196
Google Scholar
[9] Bao B C, Yang Q, Zhu L, Bao H 2019 Int. J. Bifurc. Chaos 29 10
Google Scholar
[10] Chen C, Chen J, Bao H, Chen M, Bao B 2019 Nonlinear Dyn. 95 3385
Google Scholar
[11] Bao H, Hu A, Liu W, Bao B 2020 IEEE Trans. Neural Netw. Learn. Syst. 31 502
Google Scholar
[12] 丁学利, 古华光, 贾冰, 李玉叶 2021 70 218701
Google Scholar
Ding X L, Gu H G, Jia B, Li Y Y 2021 Acta Phys. Sin. 70 218701
Google Scholar
[13] 吴莹, 徐健学, 何岱海, 靳伍银 2005 54 3457
Google Scholar
Wu Y, Xu J X, He D H, Jin W Y 2005 Acta Phys. Sin. 54 3457
Google Scholar
[14] Wang Q Y, Zhang H H, Chen G R 2012 Chaos 22 1
Google Scholar
[15] Han F, Wang Z 2015 Int. J. Nonlin. Mech. 70 105
Google Scholar
[16] Cheng L, Cao H 2017 Int. J. Bifurcat. Chaos 27 1
Google Scholar
[17] 孙晓娟, 杨白桦, 吴晔, 肖井华 2014 63 120502
Google Scholar
Sun X J, Yang B H, Wu Y, Xiao J H 2014 Acta Phys. Sin. 63 120502
Google Scholar
[18] Bao H, Zhang Y, Liu W 2020 Nonlinear Dyn. 100 937
Google Scholar
[19] Bao H, Liu W, Hu A 2019 Nonlinear Dyn. 95 43
Google Scholar
[20] Cang S, Li Y, Zhang R, Wang, Z 2019 Nonlinear Dyn. 95 381
Google Scholar
[21] Zhang X, Wang C, Yao W, Lin H 2019 Nonlinear Dyn. 97 2159
Google Scholar
[22] 张学丰, 彭良玉, 彭代鑫 2022 电子元件与材料 41 315
Google Scholar
Zhang X F, Peng D X 2022 Electron. Compon. Mater. 41 315
Google Scholar
[23] 包涵, 包伯成, 林毅, 王将, 武花干 2016 65 180501
Google Scholar
Bao H, Bao B C, Lin Y, Wang J, Wu H G 2016 Acta Phys. Sin. 65 180501
Google Scholar
[24] 谢盈, 朱志刚, 张晓锋, 任国栋 2021 70 210502
Google Scholar
Xie Y, Zhu Z G, Zhang X F, Ren G D 2021 Acta Phys. Sin. 70 210502
Google Scholar
[25] Parastesh F, Jafari S, Azarnoush H 2019 Eur. Phys. J. Spec. Top. 228 2123
Google Scholar
[26] Caputo M 1966 Ann. Geophys. 19 529
Google Scholar
下载:
计量
- 文章访问数: 3958
- PDF下载量: 110
- 被引次数: 0
