-
基于里德伯-电磁感应透明系统实现了具有宇称-时间对称的电磁感应诱导光栅, 并研究了系统中探测光场在到达光栅前形成孤子的过程以及经过光栅时引起的偏折现象. 发现由于里德伯-电磁感应透明系统具有很强的非线性光学效应, 因此只需要很少的输入探测光能量就能形成稳定的光孤子. 此外还发现, 通过改变电磁感应诱导光栅的增益/损耗系数、光栅周期、以及体系的克尔非线性非局域度都可以有效地改变探测光孤子的偏折程度和状态, 实现对弱光孤子偏折的主动操控. 本文的研究结果可为未来利用宇称-时间对称的电磁感应诱导光栅实现全光控制和光信息处理等相关应用提供一定的理论依据.Based on a Rydberg-electromagnetically-induced-transparency (Rydberg-EIT) system, an electromagnetically induced grating (EIG) with parity-time (
${\cal{PT}}$ ) symmetry is realized. The formation of solitons before the probe laser field reaching the EIG as well as its deflection when passing through the EIG are both investigated. It is found that due to the enhanced nonlinear optical effect of the Rydberg-EIT system, stable optical soliton can be formed with a very weak input light energy. In addition, it is found that by changing the gain/absorption coefficient of EIG, the period of EIG, and the nonlocality degree of optical Kerr nonlinear of the system, the deflection degree of the optical soliton can be effectively changed and manipulated. The research results of this work can provide a theoretical basis for the future applications of${\cal{PT}}$ -symmetric EIG and may be useful in the fields of all-optical manipulation and optical information processing.-
Keywords:
- Rydberg atoms /
- parity-time symmetry /
- optical solitons /
- light deflection
[1] Boettcher S, Bender C M 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[3] Makris K G, El-Ganainy R, Christodoulides D N, Musslimani Z H 2008 Phys. Rev. Lett. 100 103904
Google Scholar
[4] Feng L, El-Ganainy R, Ge L 2017 Nat. Photonics 11 752
Google Scholar
[5] Konotop V V, Shchesnovich V S, Zezyulin D A 2012 Phys. Lett. A 376 2750
Google Scholar
[6] Feng L, Ayache M, Huang J, Xu Y L, Lu M H, Chen Y F, Fainman Y 2011 Science 333 729
Google Scholar
[7] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[8] Longhi S 2010 Phys. Rev. A 82 031801(R
Google Scholar
[9] Chong Y D, Ge L, Stone A D 2011 Phys. Rev. Lett. 106 093902
Google Scholar
[10] Sun Y, Tan W, Li H, Li J, Chen H 2014 Phys. Rev. Lett. 112 143903
Google Scholar
[11] Feng L, Wong Z J, Ma R, Wang Y, Zhang X 2014 Science 346 972
Google Scholar
[12] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[13] Jin L 2018 Phys. Rev. A 97 033840
Google Scholar
[14] Hodaei H, Hassan A U, Wittek S, et al. 2017 Nature 548 187
Google Scholar
[15] Chen W, Ozdemir Ș K, Zhao G, Wiersig J, Yang L 2017 Nature 548 192
Google Scholar
[16] Jin L 2018 Phys. Rev. A 97 012121
Google Scholar
[17] Xiao L, Zhan X, Bian Z H, et al. 2017 Nat. Phys. 13 1117
Google Scholar
[18] Naghiloo M, Abbasi M, Joglekar Y N 2019 Nat. Phys. 15 1232
Google Scholar
[19] Musslimani Z H, Makris K G, El-Ganainy R, Christodoulides D N 2008 Phys. Rev. Lett. 100 030402
Google Scholar
[20] Hu S M, Ma X, Lu D, Yang Z, Zheng Y, Hu W 2011 Phys. Rev. A 84 043818
Google Scholar
[21] Shi Z, Jiang X, Zhu X, Li H 2011 Phys. Rev. A 84 053855
Google Scholar
[22] He Y, Zhu X, Mihalache D, Liu J, Chen Z 2012 Phys. Rev. A 85 013831
Google Scholar
[23] Li C Y, Huang C M, Dong L W 2013 Chin. Phys. B 22 074209
Google Scholar
[24] Hu S M, Hu W 2013 Chin. Phys. B 22 074201
Google Scholar
[25] Hang C, Huang G 2015 Phys. Rev. A 91 043833
Google Scholar
[26] Yan Z, Wen Z, Hang C 2015 Phys. Rev. E 92 022913
Google Scholar
[27] Zhou K, Wei T, Sun H, He Y, Liu S 2015 Opt. Express 23 16903
Google Scholar
[28] Hang C, Huang G 2018 Phys. Rev. A 98 043840
Google Scholar
[29] Chen Y, Yan Z, Mihalache D 2020 Phys. Rev. E 102 012216
Google Scholar
[30] Gallagher T F 2008 Rydberg Atoms (England: Cambridge University Press) pp1–9
[31] Mohapatra A K, Bason M G, Butscher B 2008 Nat. Phys. 4 89
Google Scholar
[32] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[33] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[34] Sevincli S, Henkel N, Ates C, Pohl T 2011 Phys. Rev. Lett. 107 153001
Google Scholar
[35] Pritchard J D, Weatherill K J, Adams C S 2013 Annu. Rev. Cold At. Mol. 1 301
[36] Firstenberg O, Adams C S, Hofferberth S 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152003
Google Scholar
[37] Murray C, Pohl T 2016 Advances in Atomic, Molecular, and Optical Physics (New York: Academic Press) pp321–372
[38] Zhu X Y, Xu Y L, Zou Y, Sun X C, He C, Lu M H, Liu X P, Chen Y F 2016 Appl. Phys. Lett. 109 111101
Google Scholar
[39] Liu Y M, Gao F, Fan C H, Wu J H 2017 Opt. Lett. 42 4283
Google Scholar
[40] Shui T, Yang W X, Liu S, Li L 2018 Phys. Rev. A 97 033819
Google Scholar
[41] Ma D, Yu D, Zhao X, Qian J 2019 Phys. Rev. A 99 033826
Google Scholar
[42] Hang C, Li W, Huang G 2019 Phys. Rev. A 100 043807
Google Scholar
[43] Agarwal G S, Vemuri G, Mossberg T W 1993 Phys. Rev. A 48 R4055(R
Google Scholar
[44] Bai Z, Huang G 2016 Opt. Express 24 4442
Google Scholar
[45] Bai Z, Li W, Huang G 2019 Optica 6 309
Google Scholar
[46] Hang C, Huang G, Konotop V V 2013 Phys. Rev. Lett. 110 083604
Google Scholar
[47] Hang C, Huang G 2017 Adv. Phys. X 2 737
Google Scholar
[48] Królikowski W, Bang O, Rasmussen J J, Wyller J 2001 Phys. Rev. E 64 016612
Google Scholar
[49] Lumer Y, Plotnik Y, Rechtsman M C, Segev M 2013 Phys. Rev. Lett. 111 263901
Google Scholar
-
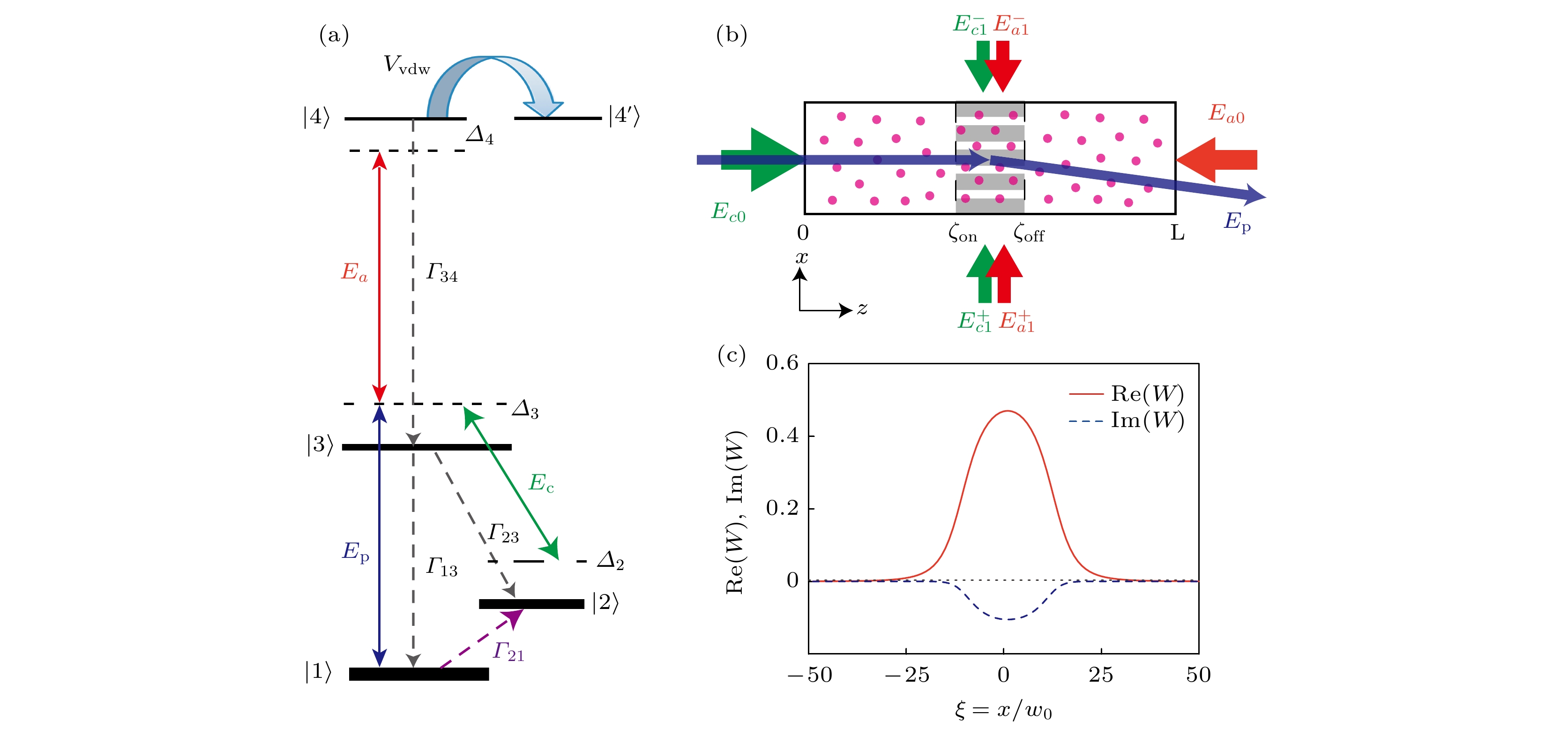
图 1 里德伯-EIT系统的能级图、装置示意图、以及非线性响应函数的空间分布 (a) 里德伯-EIT系统的能级图. 能级
$|1\rangle$ ,$|2\rangle$ , 和$|3\rangle$ 构成经典的$\Lambda$ 型EIT, 其中探测场$E_{{\rm{p}}}$ 耦合能级跃迁$|1\rangle \leftrightarrow|2\rangle$ , 控制场耦合能级跃迁$|2\rangle \leftrightarrow|3\rangle$ ,$\varDelta_{j}$ 为失谐量,$\varGamma_{jl}$ 为能级$|l\rangle$ 到能级$|j\rangle$ 的自发辐射衰减率. 里德伯能级$|4\rangle$ 通过辅助光场$E_{{\rm{a}}}$ 与能级$|3\rangle$ 远共振耦合. 引入非相干泵浦(泵浦率$\varGamma_{21}$ )将原子从能级$|1\rangle$ 泵浦到能级$|2\rangle$ . 里德伯原子之间的相互作用(即里德伯- 里德伯相互作用)由范德瓦耳斯相互作用势$V_{\rm{vdw}}$ 描述 ($V_{\rm{vdw}}$ 的表达式在文中给出). (b) 里德伯-EIT系统的装置示意图. (c) 非线性响应函数实部和虚部的空间分布, Re($W(\xi)$ )(红色实线表示)和Im($W(\xi)$ )(蓝色虚线表示); 横坐标为$\xi=x/w_0$ . 图中所用的系统参数在正文中给出Fig. 1. Level diagram and excitation scheme of the Rydberg-EIT, possible setting, and spatial distributions of the nonlinear response function. Energy levels
$|1\rangle$ ,$|2\rangle$ , and$|3\rangle$ constitute a$\Lambda$ -type EIT configuration, where the probe laser field$E_{\rm{p}}$ couples the transition$|1\rangle \leftrightarrow|2\rangle$ and the control laser field$E_{\rm{c}}$ couples the transition$|2\rangle\leftrightarrow|3\rangle$ .$\varDelta_j$ are detunings and$\varGamma_{jl}$ are the spontaneous-emission decay rate from$|l\rangle$ to$|j\rangle$ . The$\Lambda$ -type EIT is dressed by a high-lying Rydberg state$|4\rangle$ , which is far-off-resonantly coupled to state$|3\rangle$ through an assistant laser field$E_{\rm{a}}$ . An incoherent pumping (with the pumping rate$\varGamma_{21}$ ) is introduced to pump the atoms from$|l\rangle$ to$|2\rangle$ . The interaction between two Rydberg atoms is described by the van der Waals potential$V_{\rm{vdw}}$ (given in the text). (b) Possible setting of the Rydberg-EIT system. (c) Spatial distributions of the real and imaginary parts of the nonlinear response function, Re$(W)$ (the red solid line) and Im$(W)$ (the blue dashed line), as functions of$\xi=x/w_0$ 
图 2 EIG以及控制场和辅助场的空间分布 (a) EIG的实部和虚部在
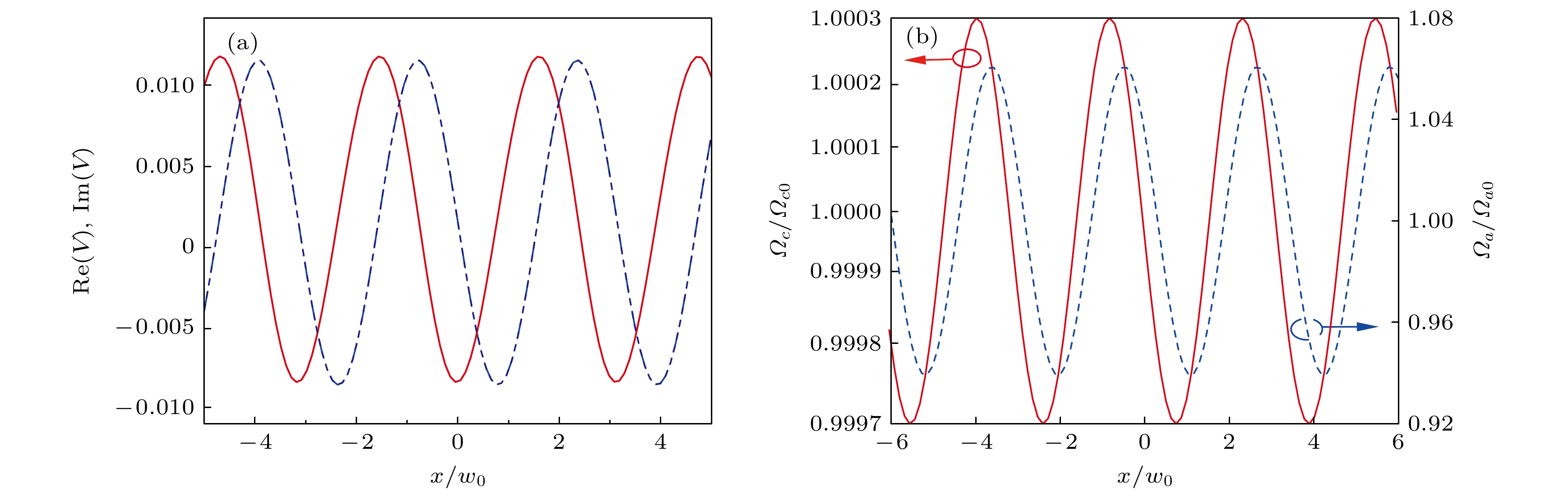
$x$ 方向上的分布, Re($V(\xi)$ )(红色实线表示)和Im($V(\xi)$ )(蓝色虚线表示); (b) 控制场和辅助场在$x$ 方向上的分布,$\varOmega_{{\rm{c}}}(\xi)/\varOmega_{{\rm{c}}0}$ (红色实线表示)和$\varOmega_{a}(\xi)/\varOmega_{a0}$ (蓝色虚线表示). 图中, 横坐标为$\xi=x/w_0$ , 调制系数取值为$V_1=V_2=0.01$ , 其他系统参数在文中给出Fig. 2. Spatial distributions of the optical potential and the control and assistant fields: (a) Real and imaginary parts of the optical potential, Re
$(V)$ (solid red line) and Im$(V)$ (blue dashed line), as functions of$\xi=x/w_0$ ; (b) half Rabi frequencies of the control and assistant fields,$\varOmega_{\rm{c}}$ (red solid line) and$\varOmega_{\rm{a}}$ (blue dashed line), as functions of$\xi=x/w_0$ . In all panels,$V_1=V_2=0.01$ . Other system parameters are given in the text
图 3 改变输入探测场振幅时探测光的传播结果 (a) 输入探测场振幅
$A=0.1$ (输入探测场能量$P_0=0.02$ ); (b)$A=1$ ($P_0= $ $ 2$ ). 其他参数取为$V_{2}=0$ ,$K=1$ , 以及$\sigma=0$ (对应于局域克尔非线性). 图(a)和图(b)中蓝色虚线和红色实线分别表示探测场的输入($z=0$ )与输出($z=10 L_{\rm{diff}}=1.4$ cm)波形.与图(a)和图(b)对应的传播过程分别在图(a1)和图(b1)中显示, 图(a1)和图(b1)中的垂直白色虚线表示EIG所在的区域Fig. 3. Propagation of probe laser field with different input amplitude: (a)
$A=0.1$ ($P_0=0.02$ ); (b)$A=1$ ($P_0=2$ ). Other system parameters are chosen as$V_{2}=0$ ,$K=1$ , and$\sigma=0$ . Panel (a1) and panel (b1) show propagation results corresponding to panel (a) and panel (b), respectively. The vertical white dashed lines in panel (a1) and panel (b1) represent the EIG regions
图 4 探测光孤子随EIG增益/吸收系数增大引起的偏折 (a) 增益/吸收系数
$V_{2}=0.5$ , 偏折角$\theta\approx\arctan 0.4$ ; (b)$V_{2}=1$ ,$\theta\approx\arctan 0.7$ ; (c)$V_{2}=1.5$ ,$\theta\approx\arctan 0.9$ . 其他参数固定为$K=1$ 以及$\sigma=0$ . 图(a)—(c)中蓝色虚线和红色实线分别表示探测场的输入($z=0$ )与输出($z=10 L_{\rm{diff}}=1.4$ cm)波形; 与图(a)—(c)对应的传播过程分别在图(a1)—(c1)中显示, 图(a1)—(c1)中的垂直白色虚线表示EIG所在的区域Fig. 4. Deflection of the probe soliton due to the increase of gain/loss coefficient of the EIG: (a)
$V_{2}=0.5$ , the deflection angle$\theta\approx\arctan 0.4$ ; (b)$V_{2}=1$ , the deflection angle$\theta\approx\arctan 0.7$ ; (c)$V_{2}=1.5$ , the deflection angle$\theta\approx\arctan 0.9$ . Other system parameters are chosen as$K=1$ and$\sigma=0$ . Panels (a1)–(c1) show propagation results corresponding to panel (a)–(c), respectively. The vertical white dashed lines in panels (a1)–(c1) represent the EIG regions
图 5 改变EIG周期引起的探测光孤子的偏折变化 (a) EIG周期为
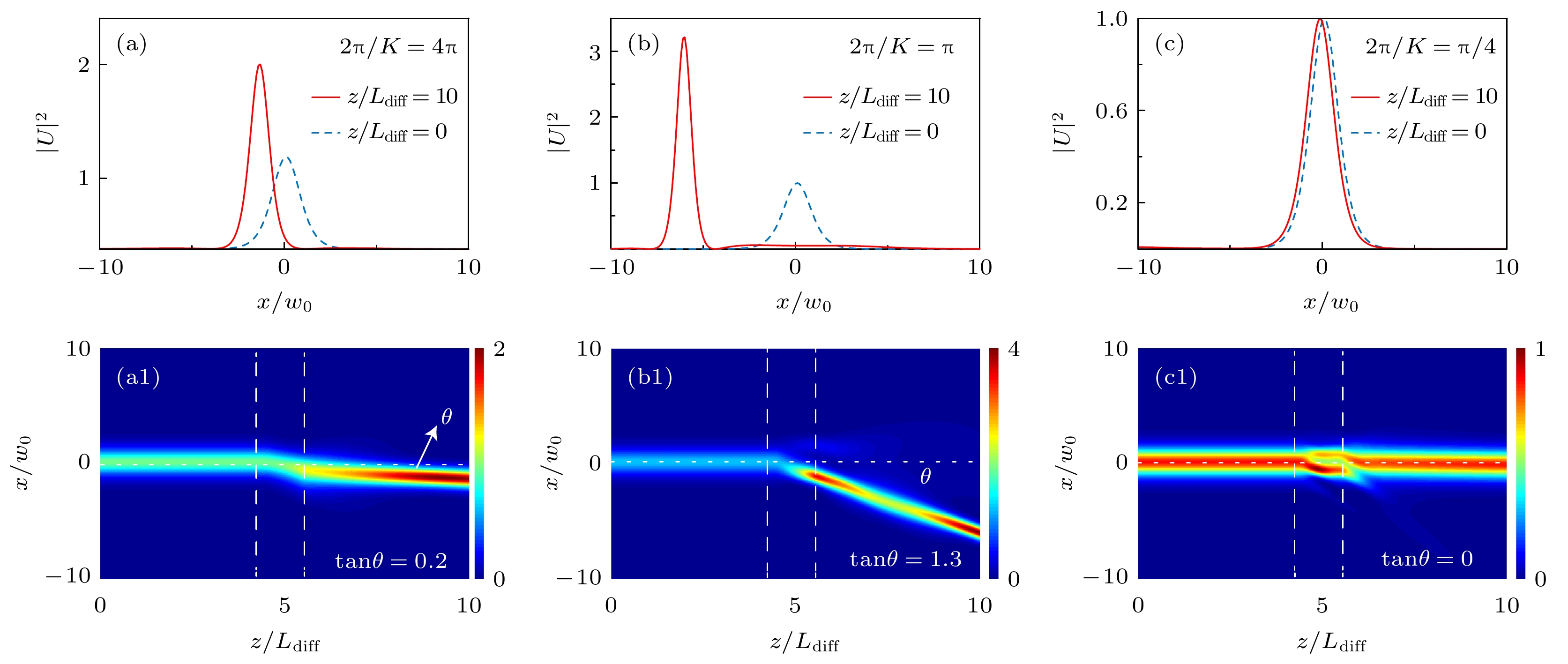
$4\pi$ ($K=0.5$ ), 偏折角$\theta\approx\arctan 0.2$ ; (b) EIG周期为$\pi$ ($K\approx $ $ 2$ ),$\theta\approx\arctan 1.3$ ; (c) EIG周期为$\pi/4$ ($K=8$ ),$\theta\approx0$ . 其他参数固定为$V_{2}=1$ 以及$\sigma=0$ . 图(a)—(c)中蓝色虚线和红色实线分别表示探测场的输入($z=0$ )与输出($z=10 L_{\rm{diff}}=1.4$ cm)波形. 与图(a)—(c)对应的传播过程分别在图(a1)—(c1) 中显示, 图(a1)—(c1)中的垂直白色虚线表示EIG所在的区域Fig. 5. Deflection of the probe soliton due to the change of the EIG period: (a) EIG period is
$4\pi$ ($K=0.5$ ), the deflection angle$\theta\approx\arctan 0.2$ ; (b) EIG period is$\pi$ ($K=2$ ), the deflection angle$\theta\approx\arctan 1.3$ ; (c) EIG period is$\pi/4$ ($K=8$ ), the deflection angle$\theta\approx0$ . Other system parameters are chosen as$V_{2}=1$ and$\sigma=0$ . Panels (a1)–(c1) show propagation results corresponding to panels (a)–(c), respectively. The vertical white dashed lines in panels (a1)–(c1) represent the EIG regions
图 6 克尔非线性非局域度发生改变时对孤子偏折带来的影响 (a) 非局域度
$\sigma=1$ (弱非局域情况), 偏折角$\theta\approx\arctan 0.7$ ; (b)$\sigma= $ $ 10$ (强非局域情况),$\theta$ 不变. 其他参数固定为$V_{2}=1$ 以及$K=1$ . 图(a)和图(b)中蓝色虚线和红色实线分别表示探测场的输入($z=0$ )与输出($z=10 L_{\rm{diff}}=1.4$ cm) 波形. 与图(a)和图(b)对应的传播过程分别在图(a1)和图(b1)中显示, 图(a1)和图(b1)中的垂直白色虚线表示EIG所在的区域Fig. 6. Deflection of the probe soliton due to the change of nonlocality degree of the Kerr nonlinearity: (a)
$\sigma=1$ (weak nonlocality), the deflection angle$\theta\approx\arctan 0.7$ ; (b)$\sigma=10$ (strong nonlocality), the deflection angle is the same. Other system parameters are chosen as$V_{2}=1$ and$K=0$ . Panels (a1) and (b1) show propagation results corresponding to panels (a) and (b), respectively. The vertical white dashed lines in panels (a1) and (b1) represent the EIG regions
图 7 孤子偏折角与EIG的增益/损耗系数以及周期的依赖关系 (a) 偏折角
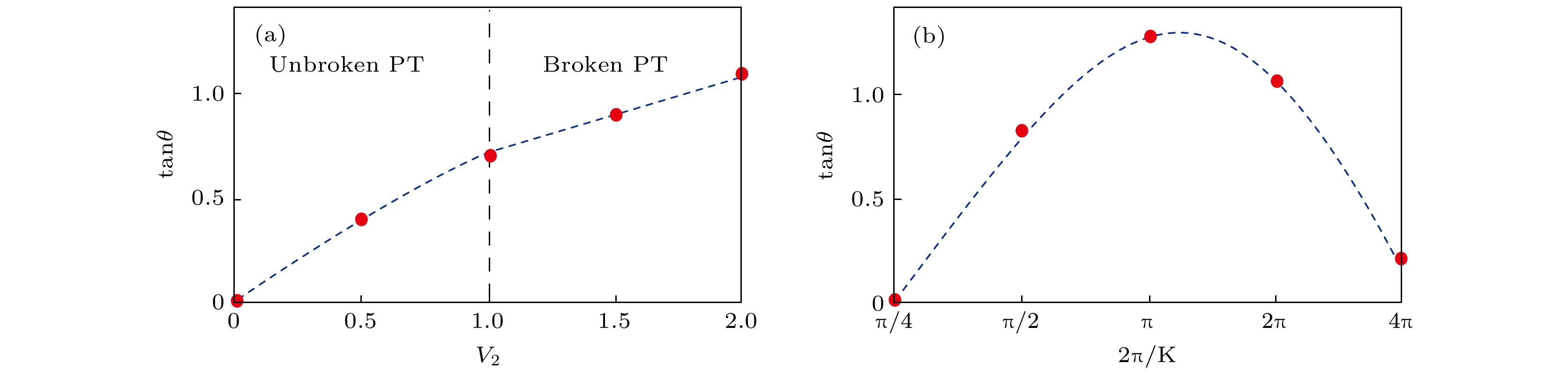
$\theta$ 与EIG的增益/损耗系数$V_2$ 的依赖关系, 其他参数固定为$K=1$ 以及$\sigma=0$ ; (b)$\theta$ 与EIG周期$2\pi/K$ 的依赖关系, 其他参数固定为$V_2=1$ 以及$\sigma=0$ . 图(a)和图(b)中的红色圆点表示数值结果, 蓝色虚线表示拟合结果Fig. 7. Deflection angle versus the gain/loss coefficient and period of the EIG: (a) The deflection angle
$\theta$ as a function of the gain/loss coefficient$V_2$ . Other system parameters are chosen as$K=1$ and$\sigma=0$ . (b)$\theta$ as a function of the period$2\pi/K$ . Other system parameters are chosen as$V_2=1$ and$\sigma=0$ . The solid red circles in panels (a) and (b) represent the numerical result while the blue dashed lines are the fit ones -
[1] Boettcher S, Bender C M 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[3] Makris K G, El-Ganainy R, Christodoulides D N, Musslimani Z H 2008 Phys. Rev. Lett. 100 103904
Google Scholar
[4] Feng L, El-Ganainy R, Ge L 2017 Nat. Photonics 11 752
Google Scholar
[5] Konotop V V, Shchesnovich V S, Zezyulin D A 2012 Phys. Lett. A 376 2750
Google Scholar
[6] Feng L, Ayache M, Huang J, Xu Y L, Lu M H, Chen Y F, Fainman Y 2011 Science 333 729
Google Scholar
[7] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[8] Longhi S 2010 Phys. Rev. A 82 031801(R
Google Scholar
[9] Chong Y D, Ge L, Stone A D 2011 Phys. Rev. Lett. 106 093902
Google Scholar
[10] Sun Y, Tan W, Li H, Li J, Chen H 2014 Phys. Rev. Lett. 112 143903
Google Scholar
[11] Feng L, Wong Z J, Ma R, Wang Y, Zhang X 2014 Science 346 972
Google Scholar
[12] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[13] Jin L 2018 Phys. Rev. A 97 033840
Google Scholar
[14] Hodaei H, Hassan A U, Wittek S, et al. 2017 Nature 548 187
Google Scholar
[15] Chen W, Ozdemir Ș K, Zhao G, Wiersig J, Yang L 2017 Nature 548 192
Google Scholar
[16] Jin L 2018 Phys. Rev. A 97 012121
Google Scholar
[17] Xiao L, Zhan X, Bian Z H, et al. 2017 Nat. Phys. 13 1117
Google Scholar
[18] Naghiloo M, Abbasi M, Joglekar Y N 2019 Nat. Phys. 15 1232
Google Scholar
[19] Musslimani Z H, Makris K G, El-Ganainy R, Christodoulides D N 2008 Phys. Rev. Lett. 100 030402
Google Scholar
[20] Hu S M, Ma X, Lu D, Yang Z, Zheng Y, Hu W 2011 Phys. Rev. A 84 043818
Google Scholar
[21] Shi Z, Jiang X, Zhu X, Li H 2011 Phys. Rev. A 84 053855
Google Scholar
[22] He Y, Zhu X, Mihalache D, Liu J, Chen Z 2012 Phys. Rev. A 85 013831
Google Scholar
[23] Li C Y, Huang C M, Dong L W 2013 Chin. Phys. B 22 074209
Google Scholar
[24] Hu S M, Hu W 2013 Chin. Phys. B 22 074201
Google Scholar
[25] Hang C, Huang G 2015 Phys. Rev. A 91 043833
Google Scholar
[26] Yan Z, Wen Z, Hang C 2015 Phys. Rev. E 92 022913
Google Scholar
[27] Zhou K, Wei T, Sun H, He Y, Liu S 2015 Opt. Express 23 16903
Google Scholar
[28] Hang C, Huang G 2018 Phys. Rev. A 98 043840
Google Scholar
[29] Chen Y, Yan Z, Mihalache D 2020 Phys. Rev. E 102 012216
Google Scholar
[30] Gallagher T F 2008 Rydberg Atoms (England: Cambridge University Press) pp1–9
[31] Mohapatra A K, Bason M G, Butscher B 2008 Nat. Phys. 4 89
Google Scholar
[32] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[33] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[34] Sevincli S, Henkel N, Ates C, Pohl T 2011 Phys. Rev. Lett. 107 153001
Google Scholar
[35] Pritchard J D, Weatherill K J, Adams C S 2013 Annu. Rev. Cold At. Mol. 1 301
[36] Firstenberg O, Adams C S, Hofferberth S 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152003
Google Scholar
[37] Murray C, Pohl T 2016 Advances in Atomic, Molecular, and Optical Physics (New York: Academic Press) pp321–372
[38] Zhu X Y, Xu Y L, Zou Y, Sun X C, He C, Lu M H, Liu X P, Chen Y F 2016 Appl. Phys. Lett. 109 111101
Google Scholar
[39] Liu Y M, Gao F, Fan C H, Wu J H 2017 Opt. Lett. 42 4283
Google Scholar
[40] Shui T, Yang W X, Liu S, Li L 2018 Phys. Rev. A 97 033819
Google Scholar
[41] Ma D, Yu D, Zhao X, Qian J 2019 Phys. Rev. A 99 033826
Google Scholar
[42] Hang C, Li W, Huang G 2019 Phys. Rev. A 100 043807
Google Scholar
[43] Agarwal G S, Vemuri G, Mossberg T W 1993 Phys. Rev. A 48 R4055(R
Google Scholar
[44] Bai Z, Huang G 2016 Opt. Express 24 4442
Google Scholar
[45] Bai Z, Li W, Huang G 2019 Optica 6 309
Google Scholar
[46] Hang C, Huang G, Konotop V V 2013 Phys. Rev. Lett. 110 083604
Google Scholar
[47] Hang C, Huang G 2017 Adv. Phys. X 2 737
Google Scholar
[48] Królikowski W, Bang O, Rasmussen J J, Wyller J 2001 Phys. Rev. E 64 016612
Google Scholar
[49] Lumer Y, Plotnik Y, Rechtsman M C, Segev M 2013 Phys. Rev. Lett. 111 263901
Google Scholar
下载:
计量
- 文章访问数: 4011
- PDF下载量: 154
- 被引次数: 0
