-
本文通过T-型石墨烯结构的条带两侧分别施加单层或者双层具有宇称-时间(parity-time, PT)对称性的虚势能, 考察了非厄米机制对能谱和边缘态的调控作用. 结果发现, 当对条带最外侧单层格点施加虚势能时, 边缘态的能量出现虚部, 并且从局域在系统两侧变为一侧. 而拓扑平庸区出现PT对称相转变. 当虚势能达到临界值时, 体态的能隙中会有新的虚能边缘态. 另一方面, 当施加双层虚势能时, 体系中会出现两种不同的边缘态. 一种是出现在顶带和底带、局域在系统一侧的边缘态, 另一种是出现在第2条和第3条能带中间、局域性相对较弱的边缘态, 且不会进入能隙中. 本工作有助于理解PT对称的边缘虚势能对T-型石墨烯结构物性的调控作用.This paper investigates the regulatory effect of non-Hermitian mechanisms on energy spectra and edge states by applying a single- or double-layer imaginary potential with parity-time (PT) symmetry to both sides of the T-graphene ribbon. The findings indicate that the type of imaginary potential applied has a significant modulation effect on the energy band structure and localization of the system. Specifically, when an imaginary potential is applied to the outermost monolayer lattice point of the ribbon, the energy of the edge state appears in the imaginary part. For its probability density distribution, its locality changes from both-sided to one-sided locality, and becomes stronger with the increase of imaginary potential. Additionally, the PT symmetry phase transition occurs in the topologically trivial region. Notably, as the imaginary potential reaches a critical value, new imaginary-energy edge state emerges within the bulk state energy gap and also shows the phenomenon that the localization is on one side of the system. Furthermore, when double-layer imaginary potentials are applied, two different edge states will appear in the system. The first type appears in the top band and the bottom band, localized on one side of the system. The second type emerges in the middle of the second energy band and the third energy band, displaying relatively weak localization and not penetrating the energy gap. This work contributes to understanding the regulatory effect of the edge imaginary potential of PT symmetry on the physical properties of T-graphene structures.
-
Keywords:
- T-graphene structure /
- parity-time symmetry /
- energy spectra /
- edge states
[1] Martinez Alvarez V M, Coutinho-Filho M D 2019 Phys. Rev. A 99 013833
 Google Scholar
Google Scholar
[2] Kitaev A Y 2001 Phys. Usp. 44 131
 Google Scholar
Google Scholar
[3] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505
 Google Scholar
Google Scholar
[4] Novoselov K S, Geim A K, Morozov S, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
 Google Scholar
Google Scholar
[5] Novoselov K, Fal'ko V, Colombo L, Gellert P R, Schwab M G, Kin K 2012 Nature 490 192
 Google Scholar
Google Scholar
[6] Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
 Google Scholar
Google Scholar
[7] Guo H M, Franz M 2009 Phys. Rev. B 80 113102
 Google Scholar
Google Scholar
[8] Liu F, Katsunori W 2017 Phys. Rev. Lett. 118 076803
 Google Scholar
Google Scholar
[9] 郭思嘉, 李昱增, 李天梓, 范喜迎, 邱春印 2022 71 070201
 Google Scholar
Google Scholar
Guo S J, Li Y Z, Li T Z, Fan X Y, Q C Y 2022 Acta Phys. Sin. 71 070201
 Google Scholar
Google Scholar
[10] Soltan-Panahi P, Struck J, Hauke P, Bick A, Plenkers W, Meineke G, Becker C, Windpassinger P, Lewenstein M, Sengstock K 2011 Nat. Phys. 7 434
 Google Scholar
Google Scholar
[11] Jo G B, Guzman J, Thomas C K, Hosur P, Vishwanath A, Stamper-Kurn D M 2012 Phys. Rev. Lett. 108 045305
 Google Scholar
Google Scholar
[12] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
 Google Scholar
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
 Google Scholar
Google Scholar
[13] Li J R, Jiang C, Su H, Qi D, Zhang L L, Gong W J 2024 Front. Phys. 19 33204
 Google Scholar
Google Scholar
[14] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
 Google Scholar
Google Scholar
[15] Li J R, Zhang L L, Zhao C H, Zhang S F, Zhu Y L, Gong W J 2024 Phys. Rev. B 109 165407
 Google Scholar
Google Scholar
[16] Yuce C 2018 Phys. Rev. A 97 042118
 Google Scholar
Google Scholar
[17] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
 Google Scholar
Google Scholar
[18] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
 Google Scholar
Google Scholar
[19] Bender C M 2007 Rep. Progr. Phys. 70 947
 Google Scholar
Google Scholar
[20] Lieu S 2018 Phys. Rev. B 97 045106
 Google Scholar
Google Scholar
[21] Jin L 2017 Phys. Rev. A 96 032103
 Google Scholar
Google Scholar
[22] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江 2022 71 177302
 Google Scholar
Google Scholar
Li J R, Wang Z A, Xu T T, Zhang L L, Gong W J 2022 Acta Phys. Sin. 71 177302
 Google Scholar
Google Scholar
[23] Wang X H, Liu T T, Xiong Y, Tong P Q 2015 Phys. Rev. A 92 012116
 Google Scholar
Google Scholar
[24] Zhao C H, Li J R, Jiang C, Zhang L L, Gong W J 2024 Phys. Rev. A 109 042203
 Google Scholar
Google Scholar
[25] Wu H C, Jin L, Song Z 2019 Phys. Rev. B 100 155117
 Google Scholar
Google Scholar
[26] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
 Google Scholar
Google Scholar
[27] Zhen B, Hsu C W, Igarashi Y C, Lu L, Kaminer I, Pick A, Chua S L, Joannopoulos J D, Soljačić M 2015 Nature 525 354
 Google Scholar
Google Scholar
[28] Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101
 Google Scholar
Google Scholar
[29] Yang Y, Yang J, Li X B, Zhao Y 2018 Phys. Lett. A 382 723
 Google Scholar
Google Scholar
[30] Kang Y T, Lu C, Yang F, Yao D X 2019 Phys. Rev. B 99 184506
 Google Scholar
Google Scholar
[31] Resta R 1994 Rev. Mod. Phys. 66 899
 Google Scholar
Google Scholar
[32] Fang C, Gilbert M J, Bernevig B A 2012 Phys. Rev. B 86 115112
 Google Scholar
Google Scholar
[33] Yan L, Zhang D, Wang X J, Yan J Y 2023 New J. Phys. 25 043020
 Google Scholar
Google Scholar
[34] 刘佳琳, 庞婷方, 杨孝森, 王正岭 2022 71 227402
 Google Scholar
Google Scholar
Liu J L, Pang T F, Yang X S, Wang Z L 2022 Acta Phys. Sin. 71 227402
 Google Scholar
Google Scholar
[35] Jin L, Song Z 2019 Phys. Rev. B 99 081103(R
 Google Scholar
Google Scholar
-
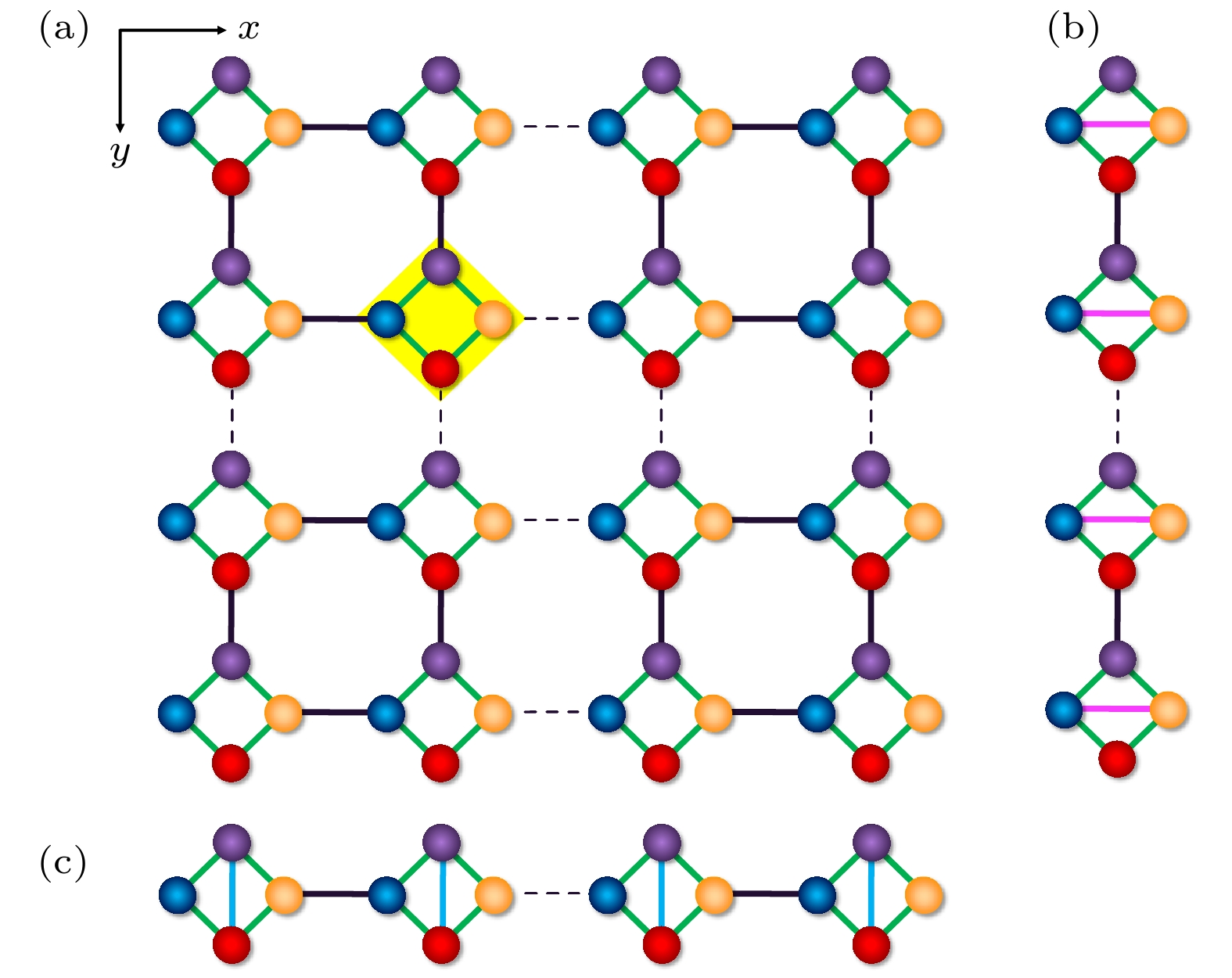
图 1 (a)二维T-型石墨烯模型; (b) x方向为周期性边界条件, y方向为开放性边界条件时T-型石墨烯一维条带模型; (c) y方向为周期性边界条件, x方向为开放性边界条件时T-型石墨烯一维条带模型, 蓝色、紫色、黄色和红色分别表示4种不同的子晶格A, B, C和D, 绿色和黑色实线分别表示胞内和胞间的跃迁, 粉色表示一维条带中新生成含$ {k}_{x} $的胞内跃迁, 浅蓝色表示一维条带中新生成含$ {k}_{y} $的胞内跃迁
Fig. 1. (a) The schematic of 2D T-graphene model; (b) one-dimensional ribbon model of T-graphene with periodic boundary conditions in the x-direction and open boundary conditions in the y-direction; (c) one-dimensional ribbon model of T-graphene with periodic boundary conditions in the y-direction and open boundary conditions in the x-direction, blue, purple, yellow, and red represent four different sublattices A, B, C and D, while green and black solid lines represent intracell and intercell hopping, the pink line represents newly generated intracell hopping contains $ {k}_{x} $, the light blue line represents newly generated intracell hopping contains $ {k}_{y} $.
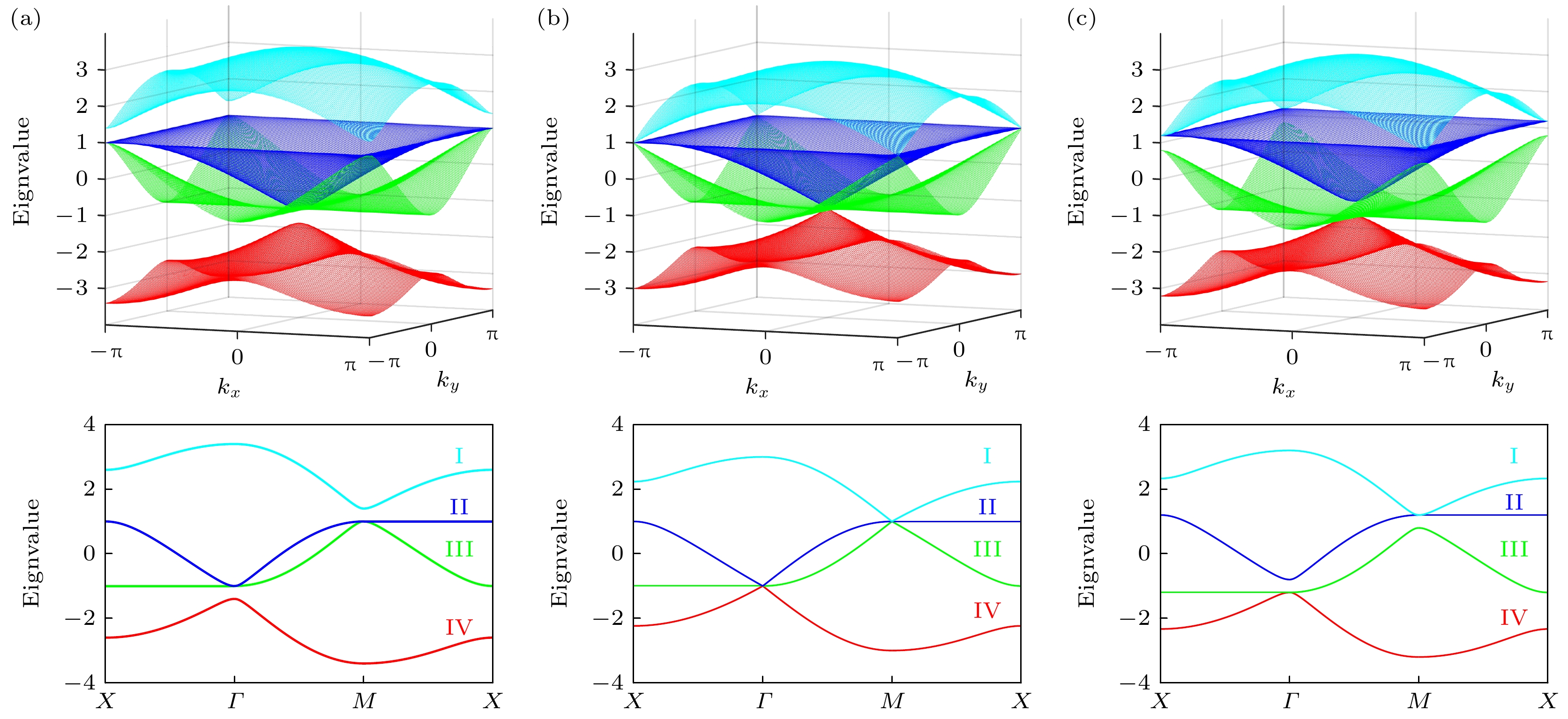
图 2 厄米情况下的T-型石墨烯能带结构图 (a)—(c)三维能带结构图和高对称点的能带图, 参数分别取为 (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $
Fig. 2. The energy band spectra of Hermitian T-graphene model: (a)–(c) Three-dimensional energy band diagrams and energy band diagrams with high symmetry points, the parameters are set as (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $.
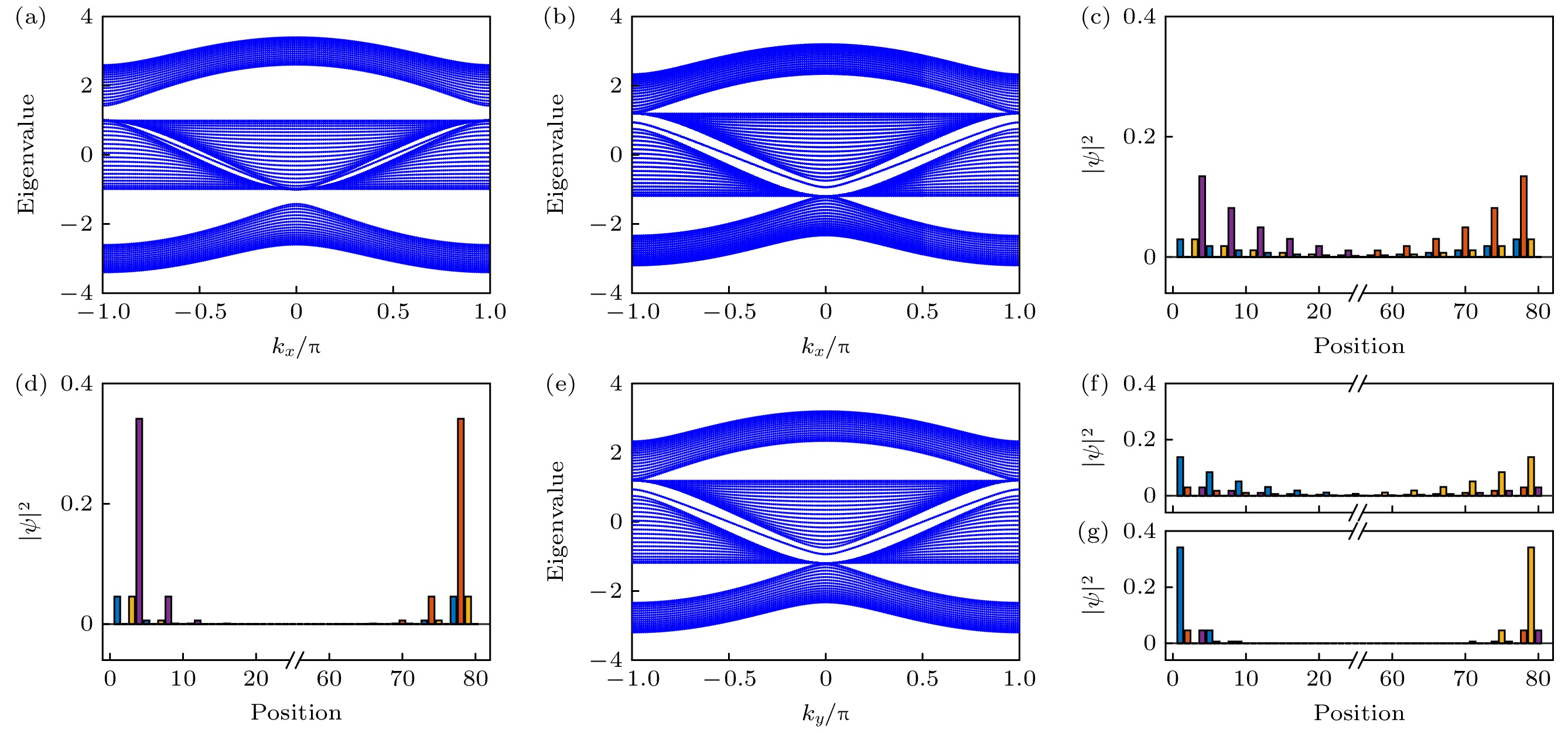
图 3 第1种条带结构的能带图, 参数分别为 (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $; 第1种条带边缘态的概率密度谱, 参数为(c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (d) $ {t}_{1} = 1 $, $ {t}_{2} = 2 $, $ {k}_{x} = 0 $; (e) 在$ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $时第2种条带结构的能带图; 第2种一维条带本征态的概率密度谱, 参数为(f) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (g) $ {t}_{1} = 1 $, $ {t}_{2} = 2 $, $ {k}_{x} = 0 $
Fig. 3. Energy band spectra of the first ribbon structure with parameters (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $; probability density spectrum of the edge state in the first ribbon structure at $ {k}_{x} = 0 $.The parameters are set as (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, (d) $ {t}_{1} = 1 $, $ {t}_{2} = 2 $; (e) energy band spectrum of the second ribbon structure at $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $; probability density spectrum of the edge state in the second ribbon structure at (f) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (g) $ {t}_{1} = 1 $, $ {t}_{2} = 2 $, $ {k}_{x} = 0 $.
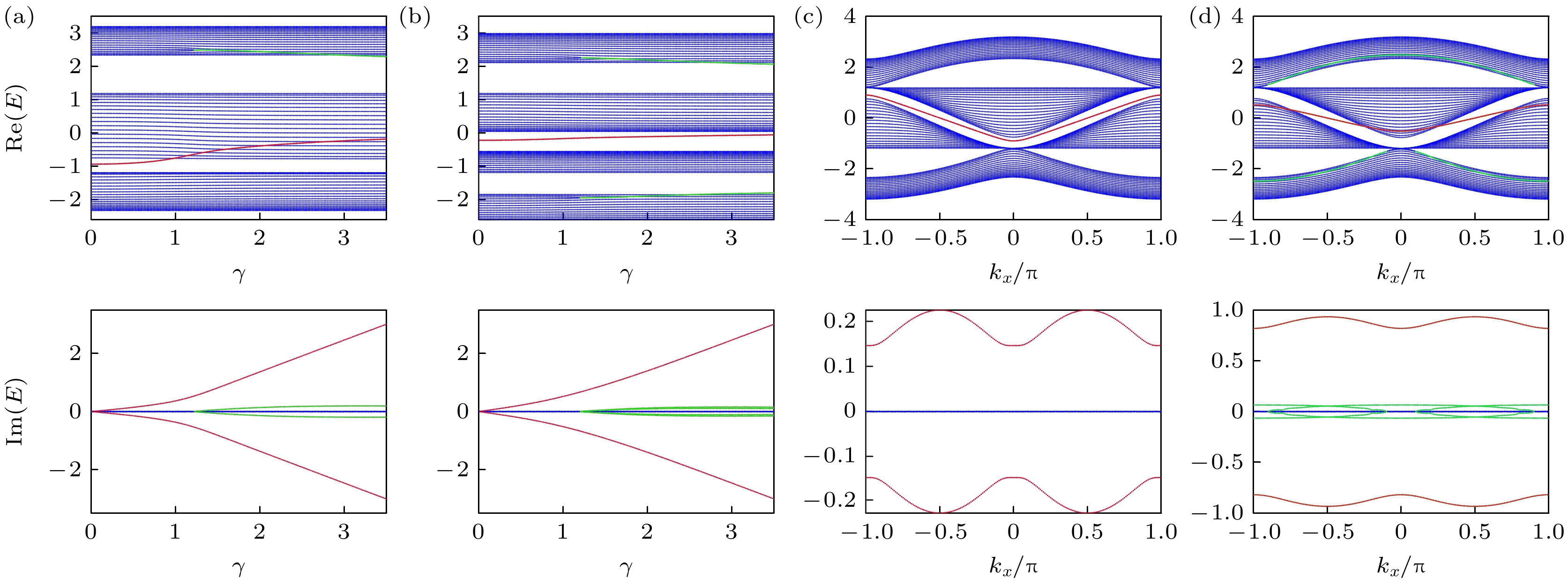
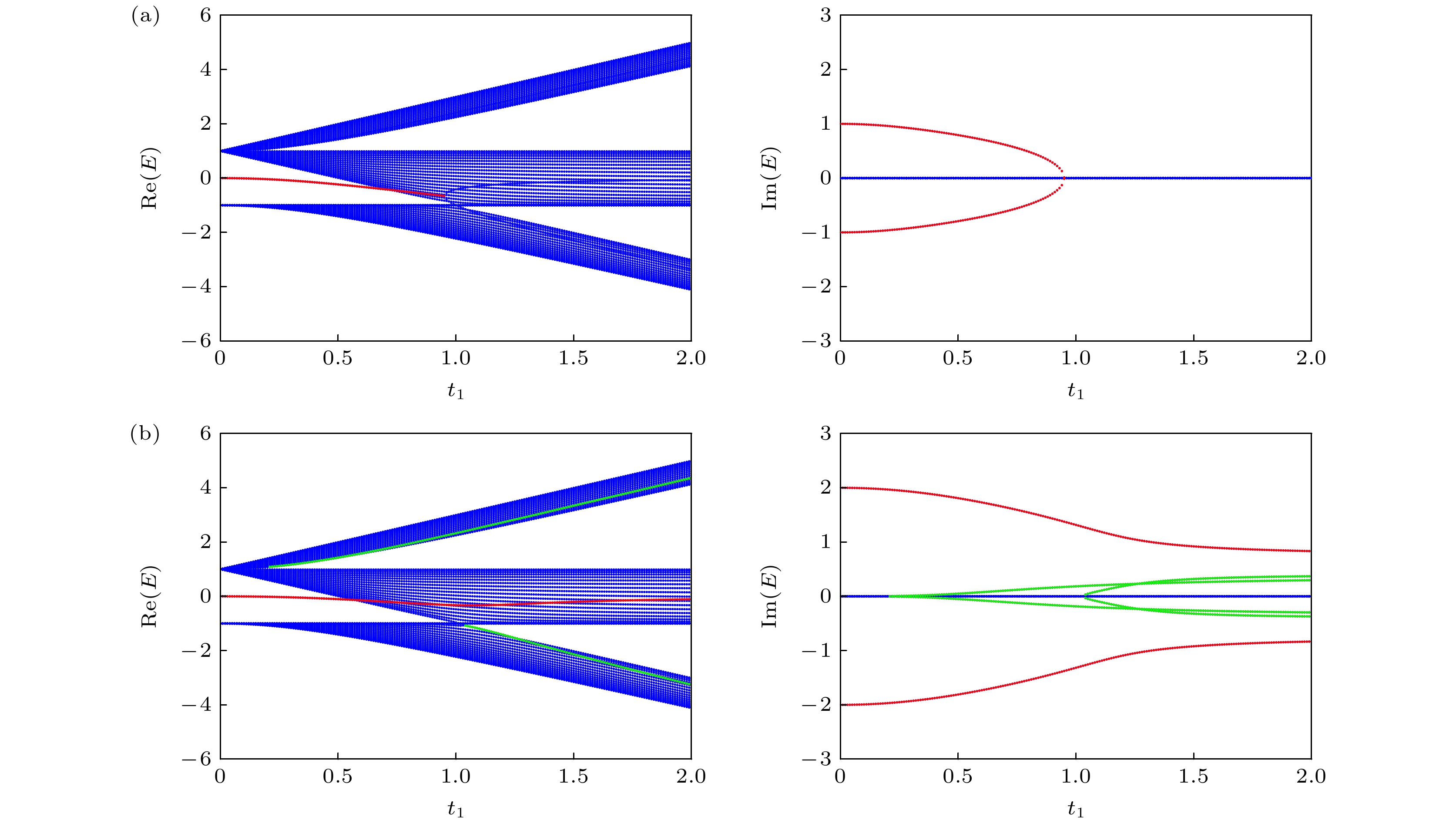
图 4 单层边缘虚势能影响下的T-型石墨烯能带 (a), (b)为本征能量与虚势能强度$ {\mathrm{\gamma }} $的关系结果, 参数取值分别为 (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $; (c), (d)为本征能量与x方向波矢量$ {k}_{x} $的关系结果, 其中(c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {\mathrm{\gamma }} = 0.5 $; (d) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {\mathrm{\gamma }} = 1.5 $, 蓝色代表的是体带部分, 红色为体系中原本存在的边缘态, 绿色为由虚势能诱导的新孤立态
Fig. 4. The band structure of the ribbon T-graphene with single layer edge imagianry potential: (a), (b) The eigenvalue spectrum of the ribbon verses $ \gamma $ with (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $; (c), (d) the band structure with (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {\mathrm{\gamma }} = 0.5 $; (d) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {\mathrm{\gamma }} = 1.5 $, blue represents the bulk states, red represents the edge state that originally existed in the system, and green represents a new isolated state induced by imaginary potential.
图 5 拓扑平庸区中单层边缘虚势能影响下的T-型石墨烯能带 (a)—(c)为本征能量与虚势能强度$ \gamma $的关系结果, 参数取值分别为 (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 0.5 $; (b) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 1 $; (c) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 1.5 $
Fig. 5. The band structure of the ribbon T-graphene with different single layer edge imagianry potential in topologically trivial region with (a) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 0.5 $; (b) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 1 $; (c) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {\mathrm{\gamma }} = 1.5 $.
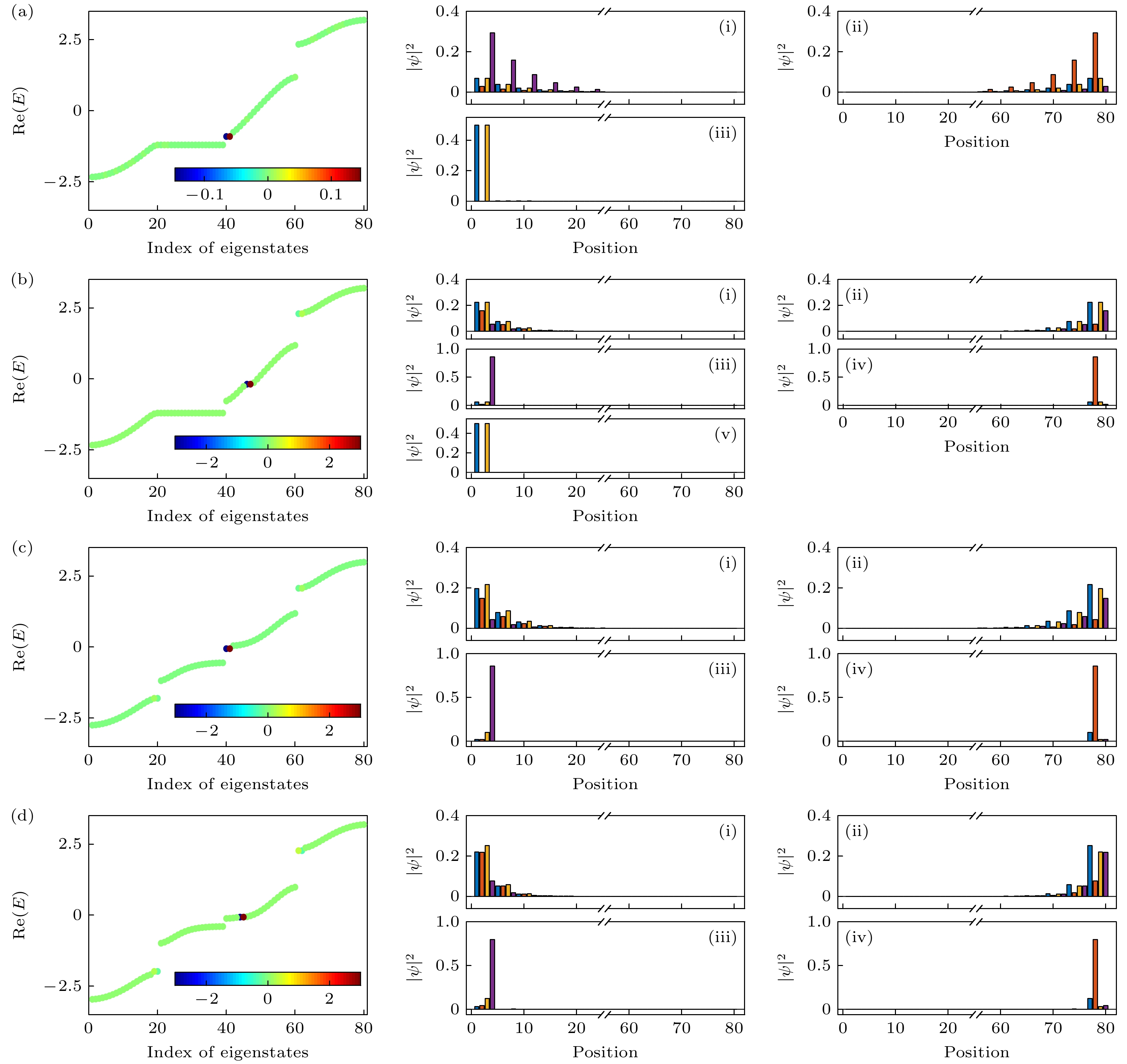
图 7 单层边缘虚势能影响下体系的本征值和概率密度密度 (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 0.5 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 3.5 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $, $ \gamma = 3.5 $; (d) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {k}_{x} = 0.4{\mathrm{\pi }} $, $ \gamma = 3.5 $
Fig. 7. Eigenvalues and probability density densities of the system under the influence of single-layer edge imaginary potential: (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 0.5 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 3.5 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $, $ \gamma = 3.5 $; (d) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $, $ \gamma = 3.5 $.
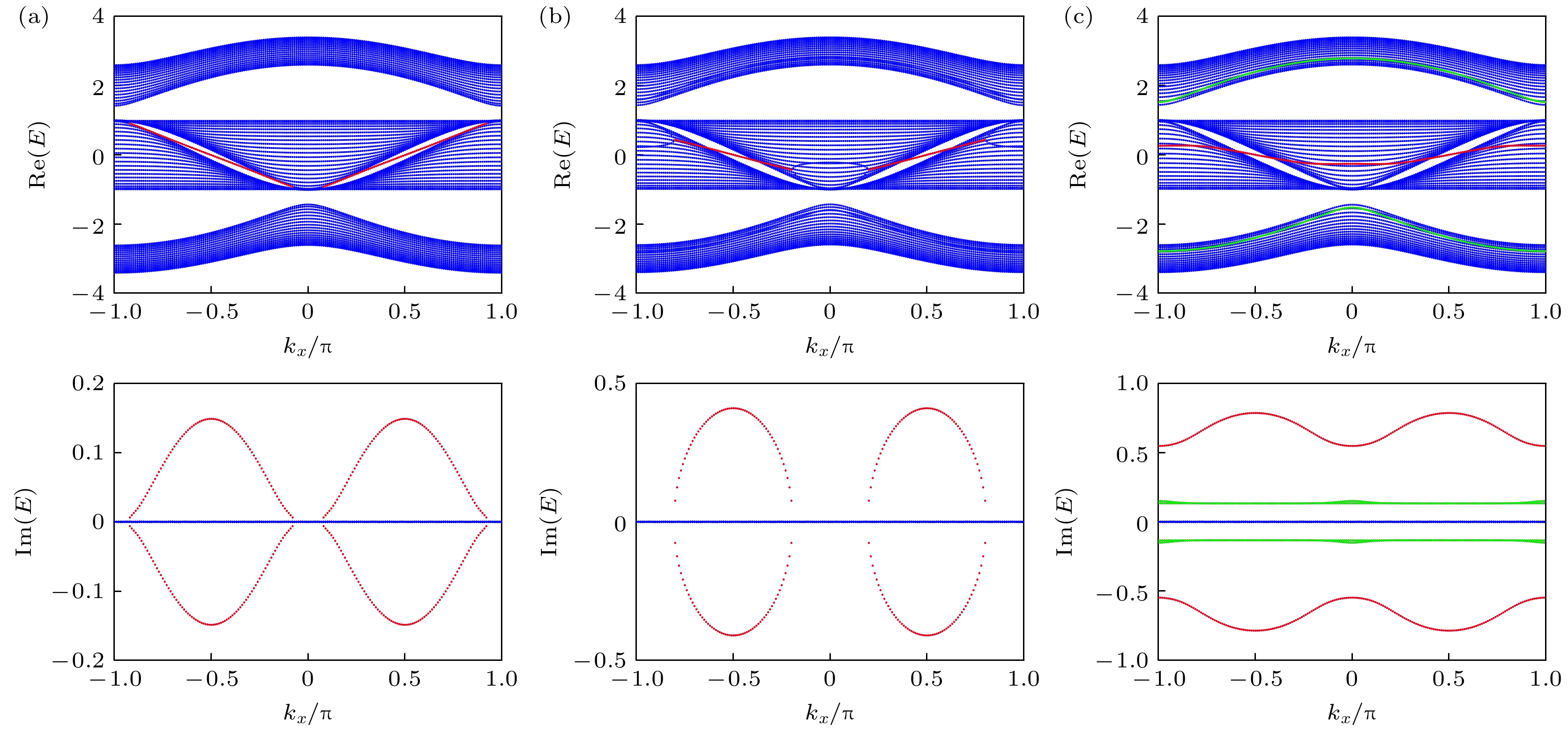
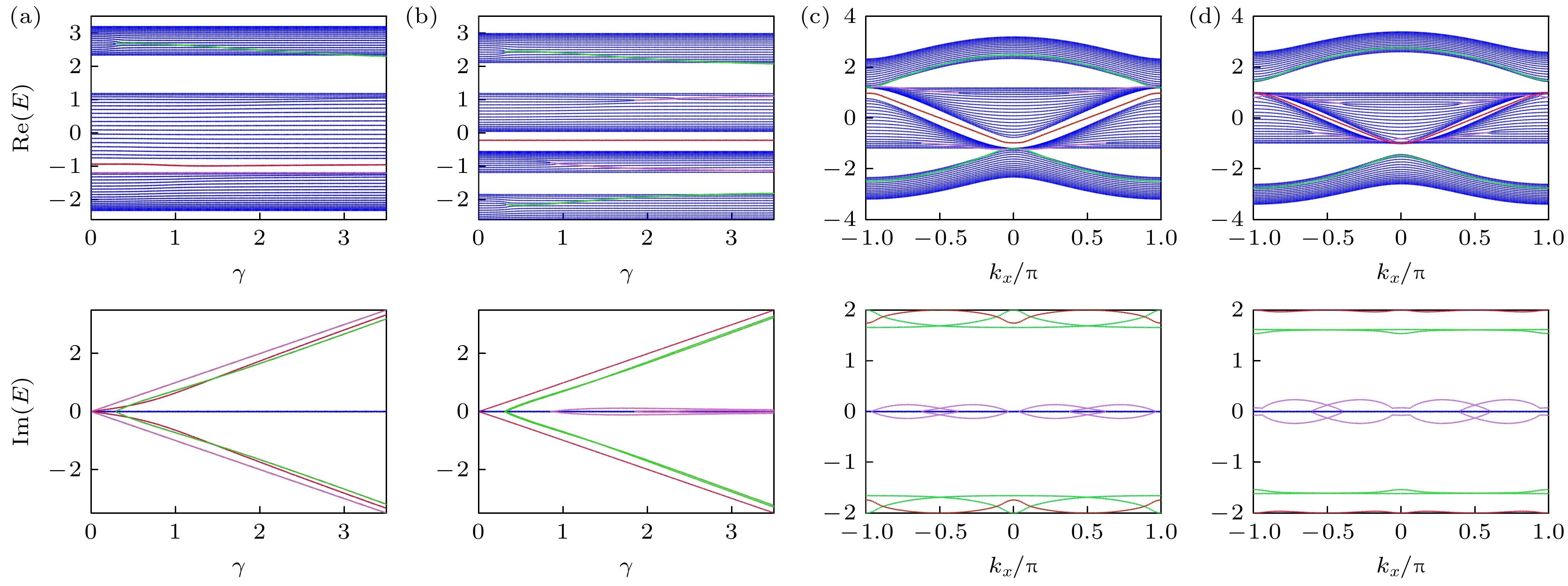
图 8 双层边缘虚势能影响下的T-型石墨烯能带 (a), (b)为体系本征值随着虚势能强度$ \gamma $变化的实部和虚部, 参数取值分别为 (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0.4{\mathrm{\pi }} $; (c), (d)为一维条带的能带结果, 参数取值为$ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $,$ \gamma = 2 $; (d) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ \gamma = 2 $
Fig. 8. The band structure of the ribbon T-graphene with double layer edge imaginary potential: The real and imaginary parts of the system eigenvalues varying with the strength of the imaginary potential $ \gamma $, the parameters are (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $; the band structure with (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {\mathrm{\gamma }} = 2 $; (d) $ {t}_{1} = 1.2 $, $ {t}_{2} = 1 $, $ \gamma = 2 $.
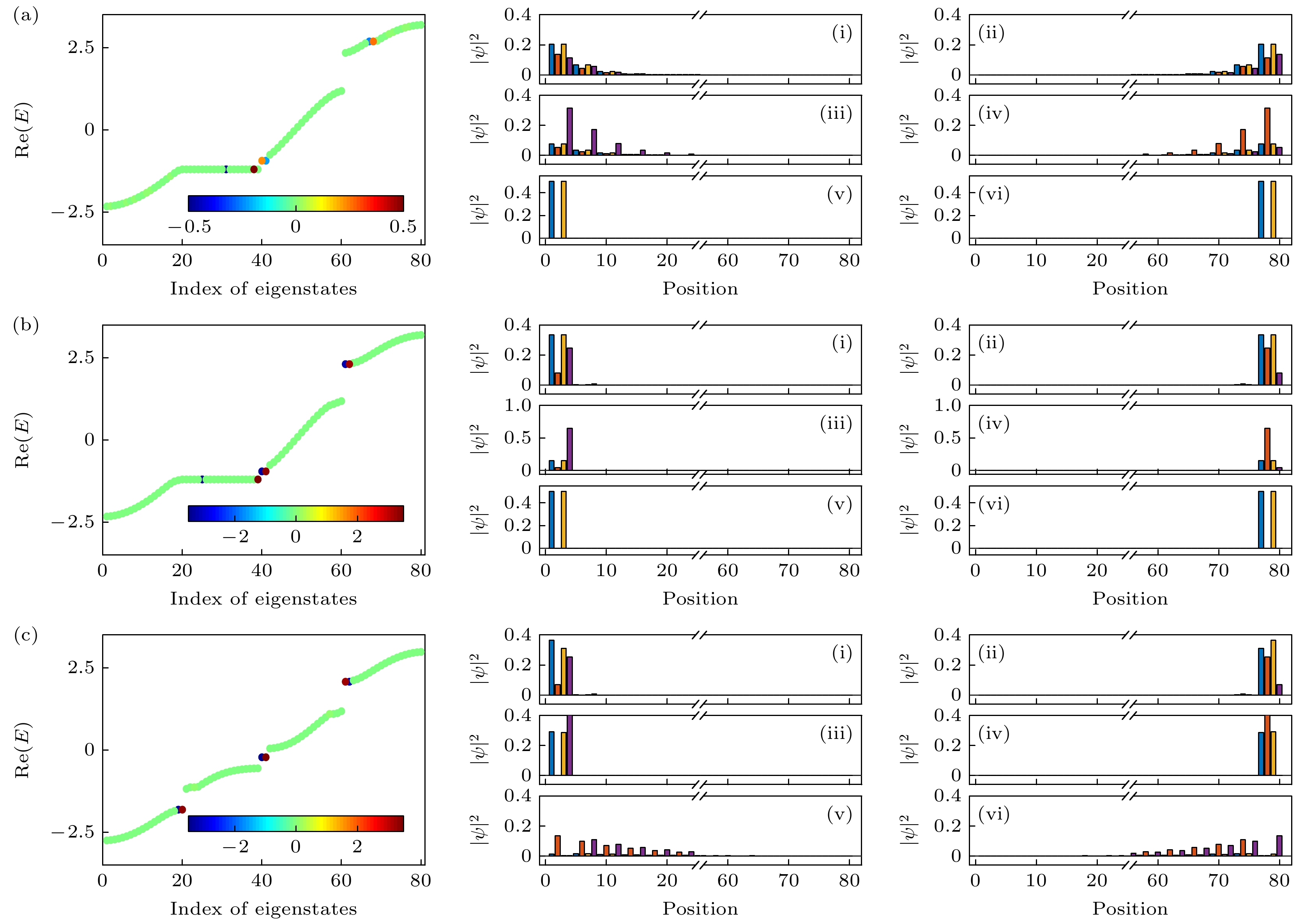
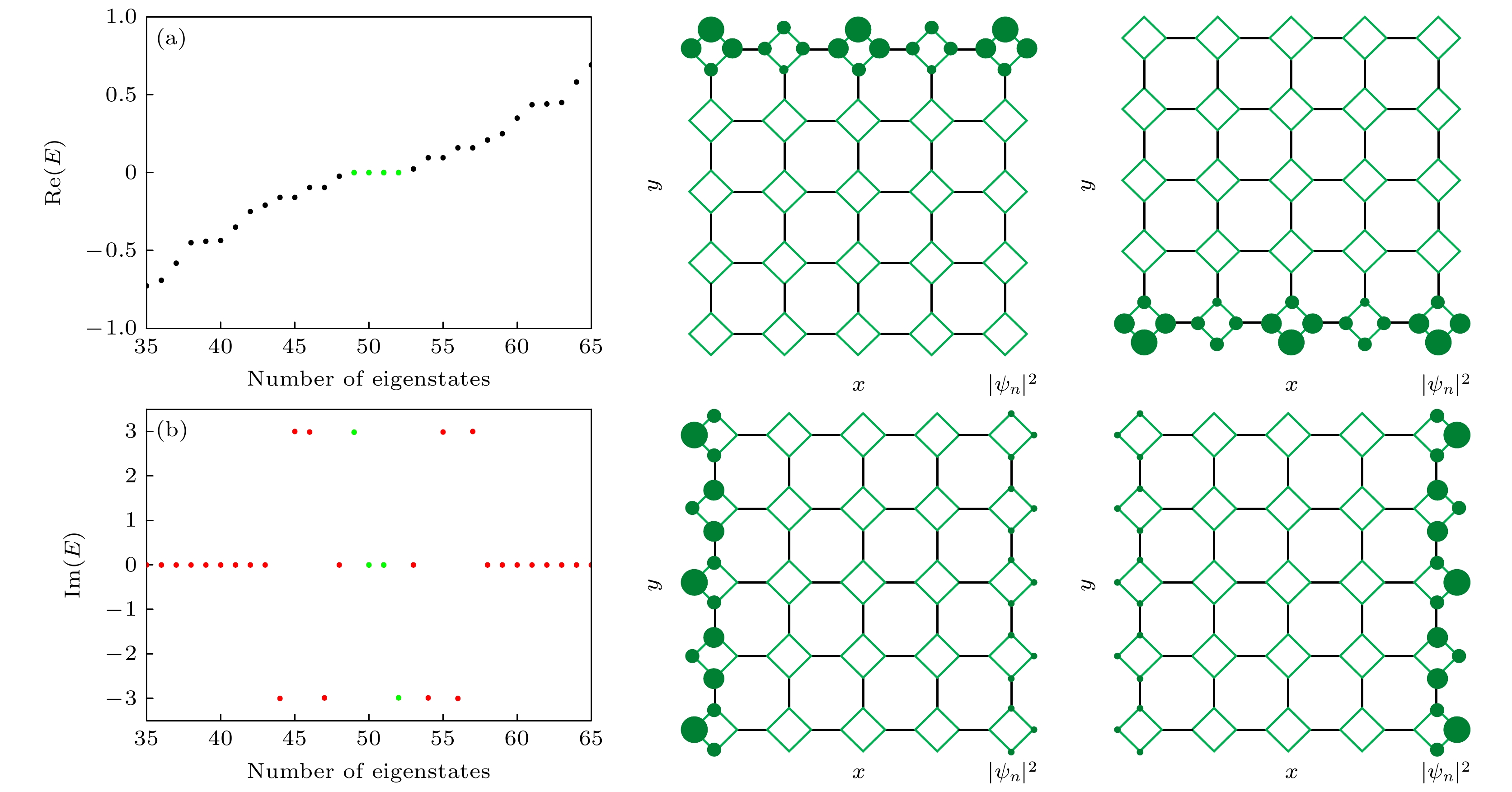
图 9 双层边缘虚势能影响下体系的本征值和概率密度谱, 参数取值分别为 (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 0.5 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 3.5 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $, $ \gamma = 3.5 $
Fig. 9. Eigenvalues and probability density densities of the system under the influence of double-layer edge imaginary potential, the parameters are set as (a) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 0.5 $; (b) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = 0 $, $ \gamma = 3.5 $; (c) $ {t}_{1} = 1 $, $ {t}_{2} = 1.2 $, $ {k}_{x} = $0.4$ {\mathrm{\pi }} $, $ \gamma = 3.5 $.
-
[1] Martinez Alvarez V M, Coutinho-Filho M D 2019 Phys. Rev. A 99 013833
 Google Scholar
Google Scholar
[2] Kitaev A Y 2001 Phys. Usp. 44 131
 Google Scholar
Google Scholar
[3] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505
 Google Scholar
Google Scholar
[4] Novoselov K S, Geim A K, Morozov S, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
 Google Scholar
Google Scholar
[5] Novoselov K, Fal'ko V, Colombo L, Gellert P R, Schwab M G, Kin K 2012 Nature 490 192
 Google Scholar
Google Scholar
[6] Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
 Google Scholar
Google Scholar
[7] Guo H M, Franz M 2009 Phys. Rev. B 80 113102
 Google Scholar
Google Scholar
[8] Liu F, Katsunori W 2017 Phys. Rev. Lett. 118 076803
 Google Scholar
Google Scholar
[9] 郭思嘉, 李昱增, 李天梓, 范喜迎, 邱春印 2022 71 070201
 Google Scholar
Google Scholar
Guo S J, Li Y Z, Li T Z, Fan X Y, Q C Y 2022 Acta Phys. Sin. 71 070201
 Google Scholar
Google Scholar
[10] Soltan-Panahi P, Struck J, Hauke P, Bick A, Plenkers W, Meineke G, Becker C, Windpassinger P, Lewenstein M, Sengstock K 2011 Nat. Phys. 7 434
 Google Scholar
Google Scholar
[11] Jo G B, Guzman J, Thomas C K, Hosur P, Vishwanath A, Stamper-Kurn D M 2012 Phys. Rev. Lett. 108 045305
 Google Scholar
Google Scholar
[12] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
 Google Scholar
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
 Google Scholar
Google Scholar
[13] Li J R, Jiang C, Su H, Qi D, Zhang L L, Gong W J 2024 Front. Phys. 19 33204
 Google Scholar
Google Scholar
[14] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
 Google Scholar
Google Scholar
[15] Li J R, Zhang L L, Zhao C H, Zhang S F, Zhu Y L, Gong W J 2024 Phys. Rev. B 109 165407
 Google Scholar
Google Scholar
[16] Yuce C 2018 Phys. Rev. A 97 042118
 Google Scholar
Google Scholar
[17] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
 Google Scholar
Google Scholar
[18] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
 Google Scholar
Google Scholar
[19] Bender C M 2007 Rep. Progr. Phys. 70 947
 Google Scholar
Google Scholar
[20] Lieu S 2018 Phys. Rev. B 97 045106
 Google Scholar
Google Scholar
[21] Jin L 2017 Phys. Rev. A 96 032103
 Google Scholar
Google Scholar
[22] 李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江 2022 71 177302
 Google Scholar
Google Scholar
Li J R, Wang Z A, Xu T T, Zhang L L, Gong W J 2022 Acta Phys. Sin. 71 177302
 Google Scholar
Google Scholar
[23] Wang X H, Liu T T, Xiong Y, Tong P Q 2015 Phys. Rev. A 92 012116
 Google Scholar
Google Scholar
[24] Zhao C H, Li J R, Jiang C, Zhang L L, Gong W J 2024 Phys. Rev. A 109 042203
 Google Scholar
Google Scholar
[25] Wu H C, Jin L, Song Z 2019 Phys. Rev. B 100 155117
 Google Scholar
Google Scholar
[26] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
 Google Scholar
Google Scholar
[27] Zhen B, Hsu C W, Igarashi Y C, Lu L, Kaminer I, Pick A, Chua S L, Joannopoulos J D, Soljačić M 2015 Nature 525 354
 Google Scholar
Google Scholar
[28] Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101
 Google Scholar
Google Scholar
[29] Yang Y, Yang J, Li X B, Zhao Y 2018 Phys. Lett. A 382 723
 Google Scholar
Google Scholar
[30] Kang Y T, Lu C, Yang F, Yao D X 2019 Phys. Rev. B 99 184506
 Google Scholar
Google Scholar
[31] Resta R 1994 Rev. Mod. Phys. 66 899
 Google Scholar
Google Scholar
[32] Fang C, Gilbert M J, Bernevig B A 2012 Phys. Rev. B 86 115112
 Google Scholar
Google Scholar
[33] Yan L, Zhang D, Wang X J, Yan J Y 2023 New J. Phys. 25 043020
 Google Scholar
Google Scholar
[34] 刘佳琳, 庞婷方, 杨孝森, 王正岭 2022 71 227402
 Google Scholar
Google Scholar
Liu J L, Pang T F, Yang X S, Wang Z L 2022 Acta Phys. Sin. 71 227402
 Google Scholar
Google Scholar
[35] Jin L, Song Z 2019 Phys. Rev. B 99 081103(R
 Google Scholar
Google Scholar
计量
- 文章访问数: 3028
- PDF下载量: 77
- 被引次数: 0













 下载:
下载: