-
利用多重尺度法解析地研究了窄脉冲探测光激发下半导体三量子点分子系统中高阶效应对光孤子稳定性的影响. 结果表明, 由标准非线性薛定谔方程所描述的光孤子在传播的过程中会出现较大衰减, 而由高阶非线性薛定谔方程所描述的光孤子却有着较为良好的稳定性. 此外, 数值模拟光孤子间的相互作用发现, 由标准非线性薛定谔方程所描述的两光孤子碰撞后其振幅迅速衰减并辐射出较为严重色散波, 而由高阶非线性薛定谔方程所描述的两光孤子碰撞后其形状几乎不发生任何变化. 这主要是由于当入射的探测光脉冲足够窄时, 系统须采用高阶方程来描述, 其物理原因是方程中的高阶效应, 包括非瞬时效应和三阶色散效应不能被忽略或当作微扰处理. 这种稳定的光孤子对于将来的光信息处理和传输技术有着潜在的应用价值.The influence of high-order effects on the stability of the optical soliton in a semiconductor three-quantum-dot molecular system under the excitation of narrow pulse probe light is analyzed analytically by using the multi-scale method. The results show that optical soliton described by the standard nonlinear Schrödinger equation will have a large attenuation in the propagation process, while the optical soliton described by the high-order nonlinear Schrödinger equation has relatively good stability. In addition, numerical simulations of the interaction between optical solitons show that the amplitudes of the two optical solitons described by the standard nonlinear Schrödinger equation attenuate rapidly after the collisions and radiation of more serious dispersion waves, while the shapes of the two optical solitons described by the high-order nonlinear Schrödinger equation hardly changes after the collision. This is mainly because when the incident probe light pulse is narrow enough, the system must be described by a higher-order equation. The physical reason is that the higher-order effects in the equation, including non-instantaneous effects and third-order dispersion effects, cannot be ignored or treated as perturbations. This kind of stable optical soliton has potential application value for future optical information processing and transmission technology.
[1] Chen S M, Tang M C, Wu J, Jiang Q, Dorogan V G, Benamara M, Mazur Y I, Salamo G J, Seeds A J, Liu H 2014 Elecctron. Lett. 50 1467
Google Scholar
[2] Sun D, Zhang H J, Sun, H, Li X W, Wang G Y 2018 Phys. Lett. A 10 036
[3] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[4] Peng Y D, Yang A H, Li D H, Zhang H G, Niu Y P, Gong S Q 2014 Laser Phys. Lett. 11 065201
Google Scholar
[5] Zeng K H, Wang D L, She Y C, Luo X Q 2013 Eur. Phys. J. D 67 221
Google Scholar
[6] Li B, Qi Y H, Niu Y P, Gong S Q 2017 J. Nonlinear Optic. Phys. Mat. 26 1750054
Google Scholar
[7] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[8] Li Z D, Wang Y Y, He P B 2019 Chin. Phys. B 28 010504
Google Scholar
[9] Si L G, Yang W X, Lu X Y, Hao X Y, Yang X X 2010 Phys. Rev. A 82 013836
Google Scholar
[10] Tian S C, Wan R G, Tong C Z, Ning Y Q, Qin L, Liu Y 2014 J. Opt. Soc. Am. B 31 1436
[11] 唐宏, 王登龙, 张蔚曦, 丁建文, 肖思国 2017 66 034202
Google Scholar
Tang H, Wang D L, Zhang W X, Ding J W, Xiao S G 2017 Acta. Phys. Sin. 66 034202
Google Scholar
[12] 杨璇, 王胤, 王登龙, 丁建文 2020 69 174203
Google Scholar
Yang X, Wang Y, Wang D L, Ding J W 2020 Acta. Phys. Sin. 69 174203
Google Scholar
[13] Yang W X, Chen A, Lee R, Wu Y 2011 Phys. Rev. A 84 013835
Google Scholar
[14] Mahmoudi M, Sahrai M 2009 Phys. E 41 1772
Google Scholar
[15] She Y C, Zheng X J, Wang D L, Zhang W X 2013 Opt. Express 21 17392
Google Scholar
[16] Hao X Y, Liu J B, Lu X Y, Song P J, Si L G 2009 Commun. Theor. Phys. 51 519
Google Scholar
[17] Zhu C J, Huang G X 2011 Opt. Express 19 1963
Google Scholar
[18] Fewo S I, Ngabireng C M, Kofane T C 2008 Phys Soc. Japan 77 074401
Google Scholar
[19] Zhang S, Yi L 2008 Phys. Rev. E 78 026602
Google Scholar
[20] Boardman A D, King N, Mitchell-Thomas R C, Malnev V N, Rapoport Y G 2008 Metamaterials 2 145
Google Scholar
[21] Boardman A D, Mitchell-Thomas R C, King N J, Rapoport Y G 2010 Opt. Commun. 283 1585
Google Scholar
[22] Boardman A D, Hess O, Mitchell-Thomas R C, Rapoport Y G, Velasco L 2010 Photon. Nanostruct. 8 228
Google Scholar
[23] Zhu C J, Huang G X 2009 Phys. Rev. B 80 235408
Google Scholar
[24] Hang C, Huang G X, Deng L 2006 Phys. Rev. E 73 036607
Google Scholar
[25] Mani Bhupeshwaran, Jawahar A, Radha S, Chitra K, Sivasubramanian A 2016 Photon. Netw. Commun. 32 73
Google Scholar
[26] Liu L, Tian B, Chai J, Chai H P 2017 Laser Phys. 27 075402
Google Scholar
[27] Borges H S, Sanz L, Villas-Bôas J M, Diniz Neto O O, Alcalde A M 2012 Phys. Rev. B 85 115425
Google Scholar
[28] Berney J, Portella-Oberli M T, Deveaud B 2008 Phys. Rev. B 77 121301
Google Scholar
[29] Bracker A S, Scheibner M, Doty M F, Stinaff E A, Ponomarev I V, Kim J C, Whitman L J, Reinecke T L, Gammon D 2006 Appl. Phys. Lett. 89 233110
Google Scholar
[30] Hsieh C Y, Shim Y P, Korkusinski M, Hawrylak P 2012 Rep. Prog. Phys. 75 114501
Google Scholar
[31] Luo X Q, Li Z Z, Jing J, Xiong W, Li T F, Yu T 2018 Sci. Rep. 8 3107
Google Scholar
[32] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[33] Wang W, Bu L, Cheng D, Ye Y, Chen S, Baronio F 2021 OSA Continuum 4 1488
Google Scholar
[34] Li L, Huang G X 2010 Eur. Phys. J. D 58 339
Google Scholar
[35] Liu J Y, Hang C, Huang G X 2016 Phys. Rev. A 93 063836
Google Scholar
[36] Luo X Q, Wang D L, Zhang Z Q, Ding J W, Liu W M 2011 Phys. Rev. A 84 033803
Google Scholar
[37] Gammon D, Snow E S, Shanabrook B V, Katzer D S, Park D 1996 Science 273 5271
[38] B N, Fei J Y, Li D F, Zhong X, Wang D, Wang H H, Bao Q Q 2020 Chin. Phys. B 29 034204
Google Scholar
-
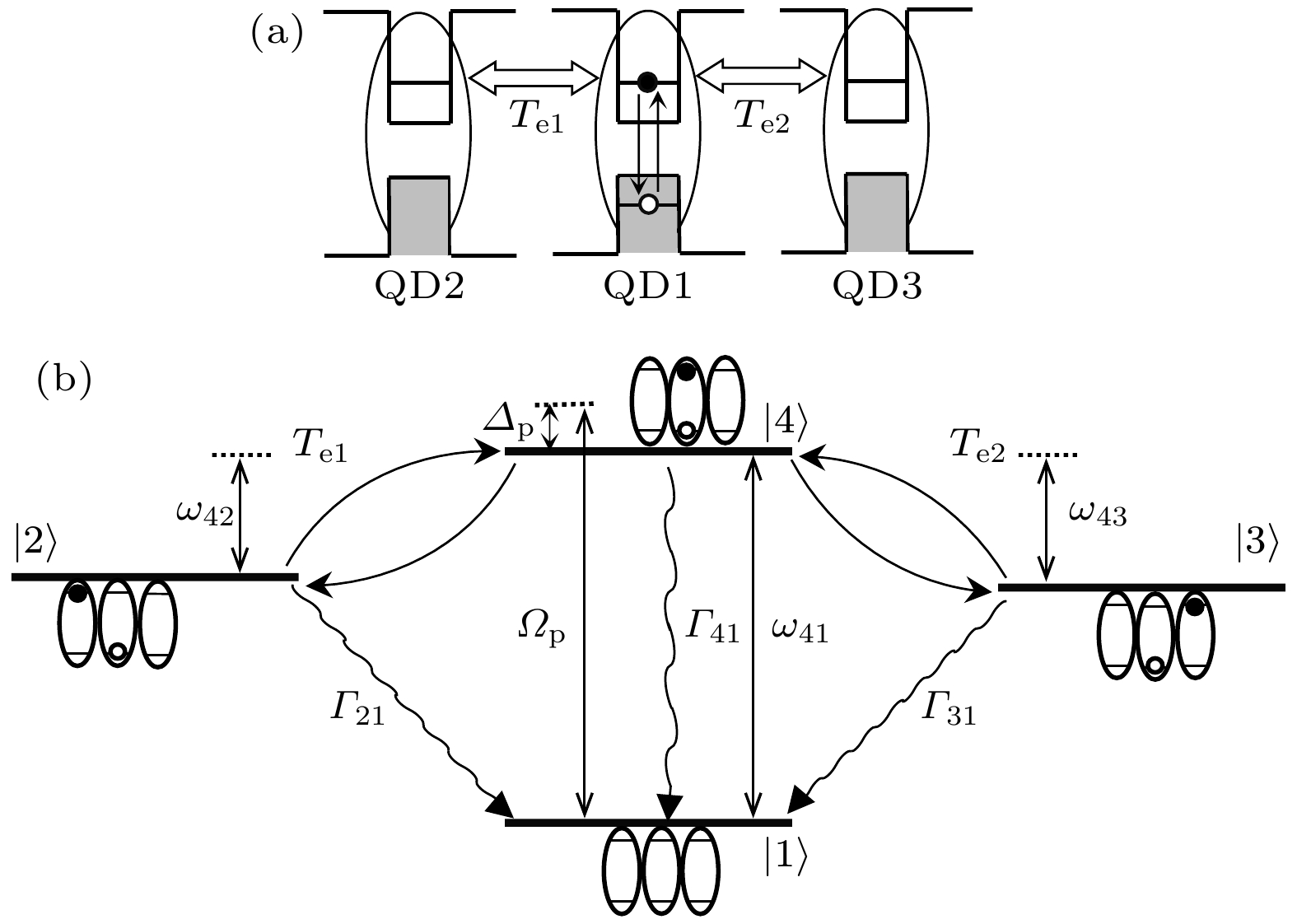
图 1 (a) TQD有效激子能级示意图; (b)相应能级结构图.
${{\varGamma} }_{m1}(m=2, 3, 4)$ 表示退相干通道,$ {\omega _{4 n}}(n = 1, 2, 3) $ 表示能级差,${\varDelta _{\text{p}}} = {\omega _{\text{p}}} - {\omega _{{\text{41}}}}$ 为探测场与能级差$ {\omega _{{\text{41}}}} $ 的频率失谐量.Fig. 1. (a) Energy level diagram of TQD effective exciton; (b) corresponding energy level structure diagram.
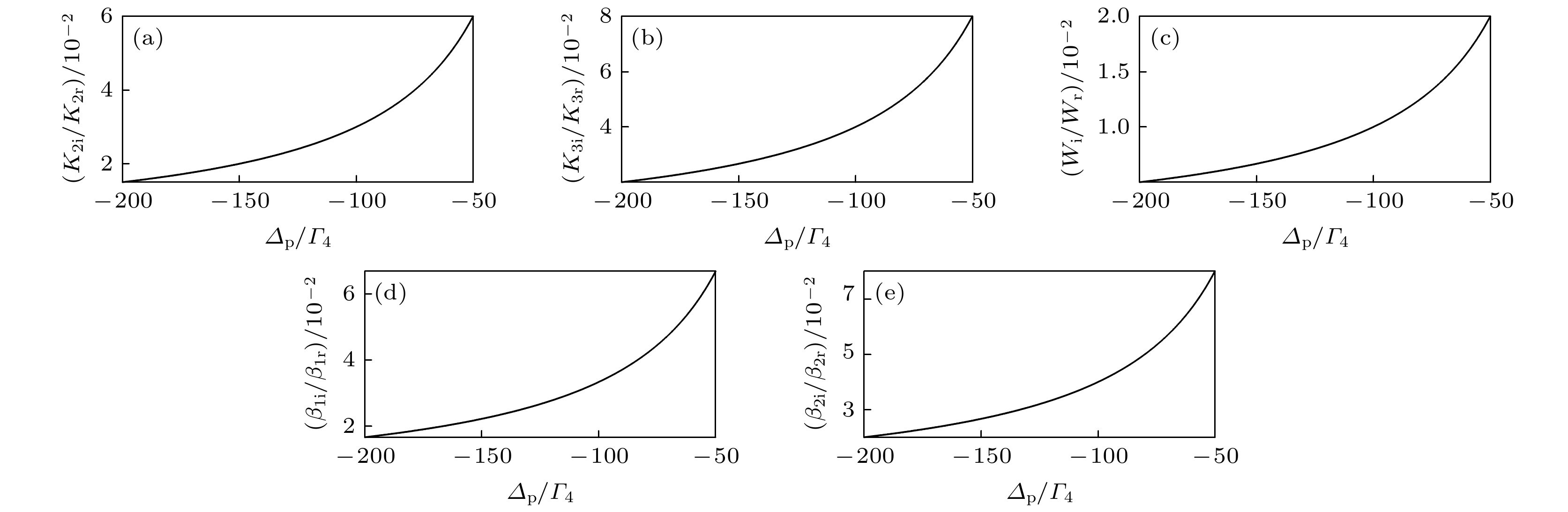
${\varGamma }_{m1} $ $ (m=2, 3, 4)$ represents the decoherent channel,${\omega _{4 n}}\left(\right.n = $ $ 1, 2, 3\left.\right)$ represents the energy level difference,${\varDelta _{\text{p}}} = {\omega _{\text{p}}} - $ $ {\omega _{{\text{41}}}}$ is the frequency detuning between the probe laser field and the energy level difference.
图 2 方程(10)相关系数虚部与实部的比值随
${{{\varDelta _{\text{p}}}}/{{\varGamma _4}}}$ 的变化关系 (a)$ {{{K_{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{2 i}}}}} {{K_{2{\text{r}}}}}}} \right. } {{K_{2{\text{r}}}}}} $ ; (b)$ {{{K_{{\text{3 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{3 i}}}}} {{K_{{\text{3 r}}}}}}} \right. } {{K_{{\text{3 r}}}}}} $ ; (c)$ {{{W_{\text{i}}}} \mathord{\left/ {\vphantom {{{W_{\text{i}}}} {{W_{\text{r}}}}}} \right. } {{W_{\text{r}}}}} $ ; (d)$ {{{\beta _{{\text{1 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{1 i}}}}} {{\beta _{{\text{1 r}}}}}}} \right. } {{\beta _{{\text{1 r}}}}}} $ ; (e)$ {{{\beta _{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{2 i}}}}} {{\beta _{{\text{2 r}}}}}}} \right. } {{\beta _{{\text{2 r}}}}}} $ Fig. 2. The ratio of the imaginary part and the real part of the correlation coefficient of equation (10) as a function of
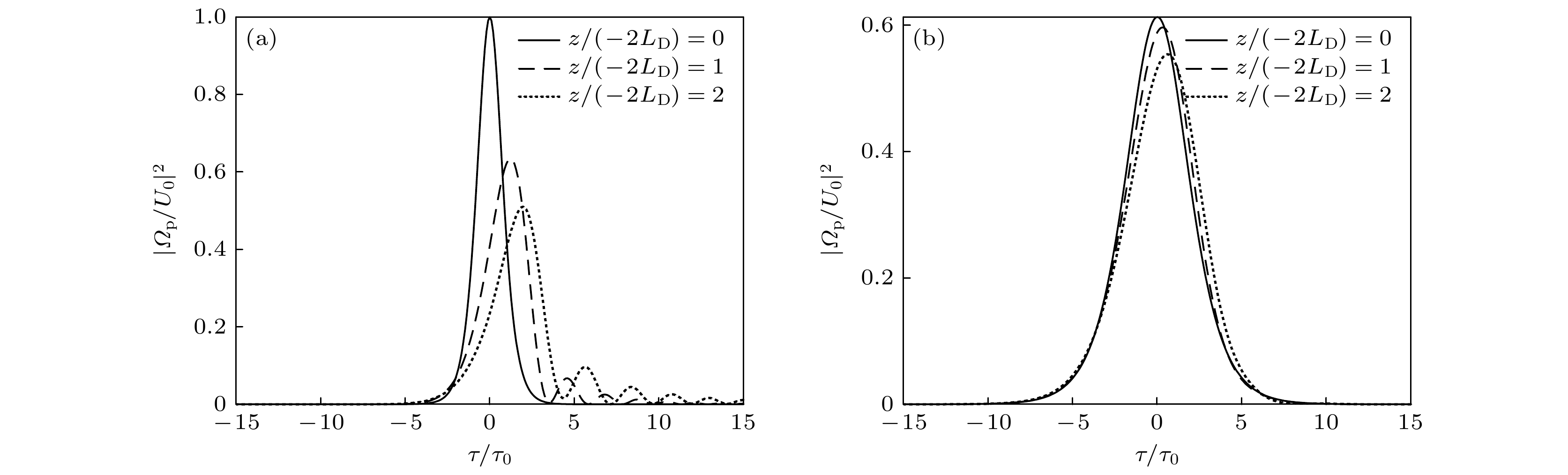
${{{\varDelta _{\text{p}}}} \mathord{\left/ {\vphantom {{{\Delta _{\text{p}}}} {{\Gamma _4}}}} \right. } {{\varGamma _4}}}$ : (a)$ {{{K_{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{2 i}}}}} {{K_{2{\text{r}}}}}}} \right. } {{K_{2{\text{r}}}}}} $ ; (b)$ {{{K_{{\text{3 i}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{3 i}}}}} {{K_{{\text{3 r}}}}}}} \right. } {{K_{{\text{3 r}}}}}} $ ; (c)$ {{{W_{\text{i}}}} \mathord{\left/ {\vphantom {{{W_{\text{i}}}} {{W_{\text{r}}}}}} \right. } {{W_{\text{r}}}}} $ ; (d)$ {{{\beta _{{\text{1 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{1 i}}}}} {{\beta _{{\text{1 r}}}}}}} \right. } {{\beta _{{\text{1 r}}}}}} $ ; (e)$ {{{\beta _{{\text{2 i}}}}} \mathord{\left/ {\vphantom {{{\beta _{{\text{2 i}}}}} {{\beta _{{\text{2 r}}}}}}} \right. } {{\beta _{{\text{2 r}}}}}} $ .
图 3 (a)方程(14)作为初始条件的数值演化结果; (b)方程(15)作为初始条件的数值演化结果. 波形给出的演化距离为1个单位长度(虚线)和2个单位长度(点虚线), 取
$ {\tau _0} = 5 \times {10^{ - 13}}\;{\text{s}} $ ,$ \beta = 0.5 $ ,$\varPhi = {\text{0}}$ , 其他参数与图2相同Fig. 3. (a) Numerical evolution result using equation (14) as the initial condition; (b) numerical evolution result using equation (15) as the initial condition. The evolution distance given by the soliton waveform is 1 unit length (dotted line) and 2 unit lengths (dotted dotted line), and the parameters used are
$ {\tau _0} = 5 \times {10^{ - 13}}\;{\text{s}} $ ,$ \beta = 0.5 $ ,$\varPhi = {\text{0}}$ , other parameters used are the same as Fig. 2
图 4 相邻孤子间的相互作用 (a)方程(16a)作为初始条件的数值演化结果; (b)方程(16b)作为初始条件的数值演化结果. 除
$ {\theta _1} = {\theta _2} = 0 $ 外, 其他参数与图2相同Fig. 4. Interaction between adjacent optical solitons: (a) Numerical evolution result using equation (16a) as the initial condition; (b) numerical evolution result using equation (16b) as the initial condition. Except for
$ {\theta _1} = {\theta _2} = 0 $ , the other parameters are the same as in Fig. 2 -
[1] Chen S M, Tang M C, Wu J, Jiang Q, Dorogan V G, Benamara M, Mazur Y I, Salamo G J, Seeds A J, Liu H 2014 Elecctron. Lett. 50 1467
Google Scholar
[2] Sun D, Zhang H J, Sun, H, Li X W, Wang G Y 2018 Phys. Lett. A 10 036
[3] Wang Y, Ding J W, Wang D L 2020 Eur. Phys. J. D 74 190
Google Scholar
[4] Peng Y D, Yang A H, Li D H, Zhang H G, Niu Y P, Gong S Q 2014 Laser Phys. Lett. 11 065201
Google Scholar
[5] Zeng K H, Wang D L, She Y C, Luo X Q 2013 Eur. Phys. J. D 67 221
Google Scholar
[6] Li B, Qi Y H, Niu Y P, Gong S Q 2017 J. Nonlinear Optic. Phys. Mat. 26 1750054
Google Scholar
[7] Chen Y, Bai Z Y, Huang G X 2014 Phys. Rev. A 89 023835
Google Scholar
[8] Li Z D, Wang Y Y, He P B 2019 Chin. Phys. B 28 010504
Google Scholar
[9] Si L G, Yang W X, Lu X Y, Hao X Y, Yang X X 2010 Phys. Rev. A 82 013836
Google Scholar
[10] Tian S C, Wan R G, Tong C Z, Ning Y Q, Qin L, Liu Y 2014 J. Opt. Soc. Am. B 31 1436
[11] 唐宏, 王登龙, 张蔚曦, 丁建文, 肖思国 2017 66 034202
Google Scholar
Tang H, Wang D L, Zhang W X, Ding J W, Xiao S G 2017 Acta. Phys. Sin. 66 034202
Google Scholar
[12] 杨璇, 王胤, 王登龙, 丁建文 2020 69 174203
Google Scholar
Yang X, Wang Y, Wang D L, Ding J W 2020 Acta. Phys. Sin. 69 174203
Google Scholar
[13] Yang W X, Chen A, Lee R, Wu Y 2011 Phys. Rev. A 84 013835
Google Scholar
[14] Mahmoudi M, Sahrai M 2009 Phys. E 41 1772
Google Scholar
[15] She Y C, Zheng X J, Wang D L, Zhang W X 2013 Opt. Express 21 17392
Google Scholar
[16] Hao X Y, Liu J B, Lu X Y, Song P J, Si L G 2009 Commun. Theor. Phys. 51 519
Google Scholar
[17] Zhu C J, Huang G X 2011 Opt. Express 19 1963
Google Scholar
[18] Fewo S I, Ngabireng C M, Kofane T C 2008 Phys Soc. Japan 77 074401
Google Scholar
[19] Zhang S, Yi L 2008 Phys. Rev. E 78 026602
Google Scholar
[20] Boardman A D, King N, Mitchell-Thomas R C, Malnev V N, Rapoport Y G 2008 Metamaterials 2 145
Google Scholar
[21] Boardman A D, Mitchell-Thomas R C, King N J, Rapoport Y G 2010 Opt. Commun. 283 1585
Google Scholar
[22] Boardman A D, Hess O, Mitchell-Thomas R C, Rapoport Y G, Velasco L 2010 Photon. Nanostruct. 8 228
Google Scholar
[23] Zhu C J, Huang G X 2009 Phys. Rev. B 80 235408
Google Scholar
[24] Hang C, Huang G X, Deng L 2006 Phys. Rev. E 73 036607
Google Scholar
[25] Mani Bhupeshwaran, Jawahar A, Radha S, Chitra K, Sivasubramanian A 2016 Photon. Netw. Commun. 32 73
Google Scholar
[26] Liu L, Tian B, Chai J, Chai H P 2017 Laser Phys. 27 075402
Google Scholar
[27] Borges H S, Sanz L, Villas-Bôas J M, Diniz Neto O O, Alcalde A M 2012 Phys. Rev. B 85 115425
Google Scholar
[28] Berney J, Portella-Oberli M T, Deveaud B 2008 Phys. Rev. B 77 121301
Google Scholar
[29] Bracker A S, Scheibner M, Doty M F, Stinaff E A, Ponomarev I V, Kim J C, Whitman L J, Reinecke T L, Gammon D 2006 Appl. Phys. Lett. 89 233110
Google Scholar
[30] Hsieh C Y, Shim Y P, Korkusinski M, Hawrylak P 2012 Rep. Prog. Phys. 75 114501
Google Scholar
[31] Luo X Q, Li Z Z, Jing J, Xiong W, Li T F, Yu T 2018 Sci. Rep. 8 3107
Google Scholar
[32] Wu Y, Deng L 2004 Phys. Rev. Lett. 93 143904
Google Scholar
[33] Wang W, Bu L, Cheng D, Ye Y, Chen S, Baronio F 2021 OSA Continuum 4 1488
Google Scholar
[34] Li L, Huang G X 2010 Eur. Phys. J. D 58 339
Google Scholar
[35] Liu J Y, Hang C, Huang G X 2016 Phys. Rev. A 93 063836
Google Scholar
[36] Luo X Q, Wang D L, Zhang Z Q, Ding J W, Liu W M 2011 Phys. Rev. A 84 033803
Google Scholar
[37] Gammon D, Snow E S, Shanabrook B V, Katzer D S, Park D 1996 Science 273 5271
[38] B N, Fei J Y, Li D F, Zhong X, Wang D, Wang H H, Bao Q Q 2020 Chin. Phys. B 29 034204
Google Scholar
下载:
计量
- 文章访问数: 3822
- PDF下载量: 58
- 被引次数: 0
