横向磁场对绝缘/导电圆管中磁气体动力学流动和传热特性的影响

赵其进; 毛保全; 白向华; 杨雨迎; 陈春林

doi:10.7498/aps.71.20220051

摘要

磁场对圆管内磁气体动力学流动和传热特性的调控作用在诸多领域具有重要的应用价值, 但目前尚缺乏相关的基础性研究. 本文考虑圆管壁面的导电性以及入口处湍流不充分发展的影响, 构建了圆管内磁气体动力学流在横向磁场作用下的物理模型和数学模型, 基于计算流体力学理论完成了数值求解, 得到了哈特曼数Ha及壁面电导率比C等因素对圆管内流动和传热特性的影响规律, 进而通过分析感应电流、电磁力和焦耳热的空间分布, 阐明了磁场对流动和传热特性的调控机理. 研究结果表明, 横向磁场作用下圆管内的湍流流动呈现各向异性分布, Hartmann边界层附近的湍流动能明显低于Roberts边界层附近, 且流速和湍流动能的各向异性随Ha的增加及流动的延伸越来越显著; 绝缘管道内, Hartmann边界层附近的速度梯度增大, 但具有大C值的导电圆管内, Roberts边界层内的速度梯度反而大于Hartmann边界层附近; 横向磁场对圆管内的传热具有抑制作用, 对于不同的C值, 平均努塞尔数都随Ha的增加呈现先减小后增大的趋势, 即传热抑制存在“饱和效应”; 圆管内流动特性的转变源于磁场与流体耦合作用下电磁力的变化, 而传热特性的转变源于磁场对湍流的抑制以及焦耳热效应的耦合作用.

关键词:

Abstract

The regulating effect of magnetic field on magnetogasdynamic flow and heat transfer characteristics in circular tubes has important applications in many fields, but there is still a lack of relevant basic research. Considering the conductivity of the tube wall and the insufficient development of turbulence, the physical model and mathematical model of magnetogasdynamic flow in a circular tube under a given transverse magnetic field are constructed, and the numerical algorithm is designed within a theoretical framework of the finite volume method. The effect of factors including Hartman number (Ha) and wall conductivity ratio (C) on the flow and heat transfer characteristics are obtained through analyzing the distributions of velocity, turbulent kinetic energy, and temperature. Furthermore, the regulation mechanism of the transverse magnetic field is discussed by analyzing the spatial distribution of induced current, electromagnetic force and Joule heat. The results show that the distribution of velocity and the distribution of turbulent kinetic energy in the circular tube under a given transverse magnetic field are both anisotropic. The turbulent kinetic energy near the Hartmann boundary layer is much lower than that near the Roberts boundary layer, and the anisotropic distribution of velocity and turbulent kinetic energy become more and more evident with the increase of Ha and the extension of the flow. The transverse magnetic field has a suppression effect on the heat transfer in the tube. 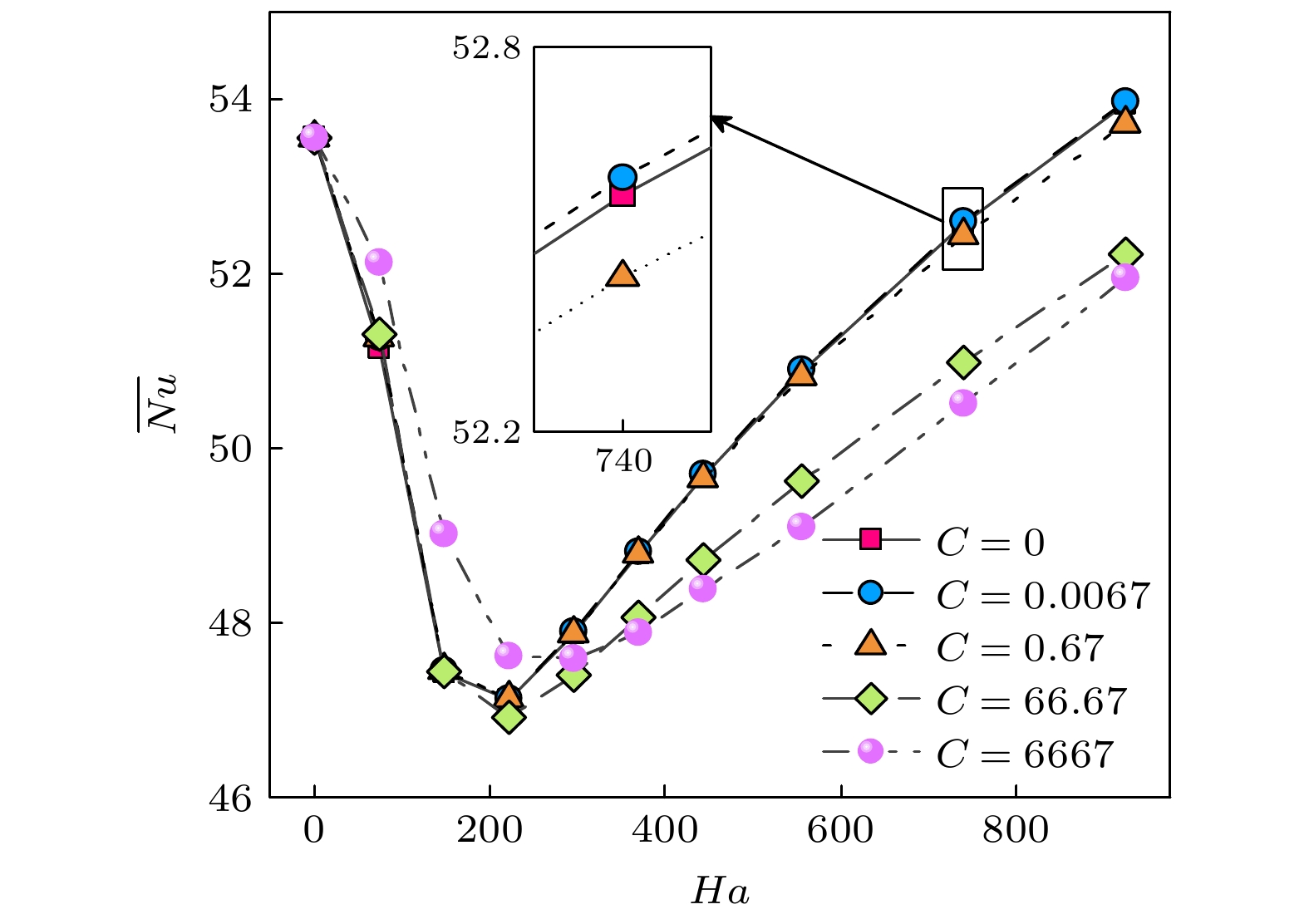For different values of C, the average Nusselt number ($ \overline {Nu} $) shows a first-decreasing-and-then-increasing trend with Ha increasing, that is, there is a “saturation effect” in heat transfer suppression. When the wall conductivity is small (C $\leqslant $ 0.67), the change of $ \overline {Nu} $ under the condition of conductive wall is basically consistent with that of an insulating wall. However, when C exceeds a certain value (C $\geqslant $ 66.67), the $ \overline {Nu} $ under the condition of small Ha increases in comparison with that of the insulating wall, while the $ \overline {Nu} $ decreases under the condition of large Ha . The change of flow characteristics in the circular tube results from the variation of electromagnetic force under the coupling of magnetic field and fluid, while the change of heat transfer characteristics originates from the coupling effect of the suppression of turbulence and the Joule heating. When Ha is small, the suppression effect of the magnetic field on turbulence is dominant, and the $ \overline {Nu} $ decreases with the increase of Ha. When Ha exceeds a certain value (Ha $\geqslant $ 222), the large accumulation of Joule heat in the circular tube enhances the heat transfer, resulting in the increase of the $ \overline {Nu} $ with the continuous increase of Ha.

Keywords:

作者及机构信息

陆军装甲兵学院兵器与控制系, 北京　100072

通信作者: 毛保全, mbq123321@126.com

基金项目: 国家自然科学基金青年科学基金(批准号: 52006241)资助的课题

Authors and contacts

Weapons and Control Department, Army Academy of Armored Forces, Beijing 100072, China

Corresponding author: Mao Bao-Quan, mbq123321@126.com

Funds: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 52006241).

文章全文 : translate this paragraph

参考文献

[1]	Bedick C R, Woodside C R, Baylor R, Paul-Irudayaraj M 2020 Combust. Flame 213 140 Google Scholar
[2]	Zhao K, Lu Y, Li F, Hu J, Ming M, Wang X, Li S 2020 Acta Astronaut. 171 257 Google Scholar
[3]	Kim K S, Lee S H, Yun Y, Kwon S 2020 Acta Astronaut. 173 31 Google Scholar
[4]	Veefkind A 2004 IEEE T. Plasma Sci. 32 2197 Google Scholar
[5]	Wang Y, Ma T, Pei D, Chen C, Zhang D, Li C 2020 IEEE T. Plasma Sci. 48 1008 Google Scholar
[6]	李程, 毛保全, 白向华, 李晓刚 2018 兵工学报 39 851 Google Scholar Li C, Mao B Q, Bai X H, Li X G 2018 Acta Armam. 39 851 Google Scholar
[7]	成玉国, 夏广庆 2017 66 075204 Google Scholar Cheng Y G, Xia Y G 2017 Acta Phys. Sin. 66 075204 Google Scholar
[8]	Hedlund B, Houpt A, Gordeyev S, Leonov S 2018 AIAA J. 56 2699 Google Scholar
[9]	丁明松, 傅杨奥骁, 高铁锁, 董维中, 江涛, 刘庆宗 2020 69 214703 Google Scholar Ding M S, Fu Y A X, Gao T S, Dong W Z, Jiang T, Liu Q Z 2020 Acta Phys. Sin. 69 214703 Google Scholar
[10]	Mistrangelo C, Bühler L, Smolentsev S, Klüber V, Maione I, Aubert J 2021 Fusion Eng. Des. 173 112795 Google Scholar
[11]	Maurya A, Kumar R, Jha P K 2020 J. Manuf. Process. 60 596 Google Scholar
[12]	Yang R J, Hou H H, Wang Y N, Fu L M 2016 Sensor. Actuat. B-Chem. 224 1 Google Scholar
[13]	Moitoi A J, Shaw S 2022 Microvasc. Res. 139 104262 Google Scholar
[14]	Erdem M, Varol Y 2020 J. Therm. Anal. Calorim. 139 3897 Google Scholar
[15]	Krasnov D, Zikanov O, Boeck T 2012 J. Fluid Mech. 704 421 Google Scholar
[16]	Zikanov O, Krasnov D, Boeck T, Sukoriansky S 2019 J. Fluid Mech. 867 661 Google Scholar
[17]	Chatterjee D, Gupta S K J 2016 Appl. Fluid Mech. 9 2167 Google Scholar
[18]	Belyaev I, Sardov P, Melnikov I, Frick P 2021 Int. J. Therm. Sci. 161 106773 Google Scholar
[19]	Chaudhary R, Vanka S P, Thomas B G 2010 Phys. Fluids 22 075102 Google Scholar
[20]	Hunt J C R 1965 J. Fluid Mech. 21 577 Google Scholar
[21]	Tao Z, Ni M J 2015 Sci. China Phys. Mech. 58 024701
[22]	Zhang X, Pan C, Xu Z 2017 Fusion Eng. Des. 125 647 Google Scholar
[23]	Artemov V I, Makarov M V, Minko K B, Minko K B, Yankov G G 2020 Int. J. Heat Mass Tran. 146 118822 Google Scholar
[24]	Singh R J, Gohil T B 2019 Comput. Fluids 179 476 Google Scholar
[25]	Yarahmadi M, Goudarzi H M, Shafii M B 2015 Exp. Therm. Fluid Sci. 68 601 Google Scholar
[26]	Sha L, Ju Y, Zhang H, Wang J 2017 Appl. Therm. Eng 113 566 Google Scholar
[27]	Abadeh A, Sardarabadi M, Abedi M, Pourramezan M, Passandideh-Fard M, Maghrebi M 2020 J. Mol. Liq. 299 112206 Google Scholar
[28]	Shahsavar A, Saghafian M, Salimpour M R, Shafii M B 2016 Exp Therm. Fluid Sci. 76 1 Google Scholar
[29]	Afrand M, Karimipour A, Nadooshan A A, Akbari M 2016 Physica. E 84 474 Google Scholar
[30]	Khosravi A, Malekan M 2019 Eur. Phys. J. Plus 134 1 Google Scholar
[31]	Malekan M, Khosravi A 2018 Powder Techno. 333 364 Google Scholar
[32]	Hussam W K, Hamid A H A, Ng Z Y, Sheard G J 2018 Int. J. Therm. Sci. 134 453 Google Scholar
[33]	李开, 刘伟强 2016 65 064701 Google Scholar Li K, Liu W Q 2016 Acta Phys. Sin. 65 064701 Google Scholar
[34]	Liu Z, Li Y, Su Y 2018 Int. J. Adv. Manuf. Tech. 98 2015 Google Scholar
[35]	Tsilingiris P T 2008 Energ. Convers. Manage. 49 1098 Google Scholar
[36]	Stephan K, Laesecke A 1985 J. Phys. Chem. Ref. Data 14 227 Google Scholar
[37]	Menter F R 1994 AIAA J. 32 1598 Google Scholar
[38]	Widlund O, Zahrai S, Bark F H 1998 Phys. Fluids 10 1987 Google Scholar
[39]	Walker J S 1981 Journal de Mécanique 20 79
[40]	Takeuchi J, Satake S, Morley N B, Kunugi T, Yokomine T, Abdou, M A 2008 Fusion Eng. Des. 83 1082 Google Scholar
[41]	Gnielinski V 1976 Int. Chem. Eng 16 359
[42]	Bradshaw P 1974 Nature 249 135

施引文献

图 1 物理模型示意图

Fig. 1. Schematic diagram of physical model.

下载: 全尺寸图片幻灯片

图 2 不同Ha下圆管yz截面上沿z = 0方向的流速数值解与文献[40]中实验数据的对比

Fig. 2. Comparison between the numerical solution of flow velocities along z = 0 direction on the yz cross-section of the circular tube under different Ha and the experimental results in reference [40].

下载: 全尺寸图片幻灯片

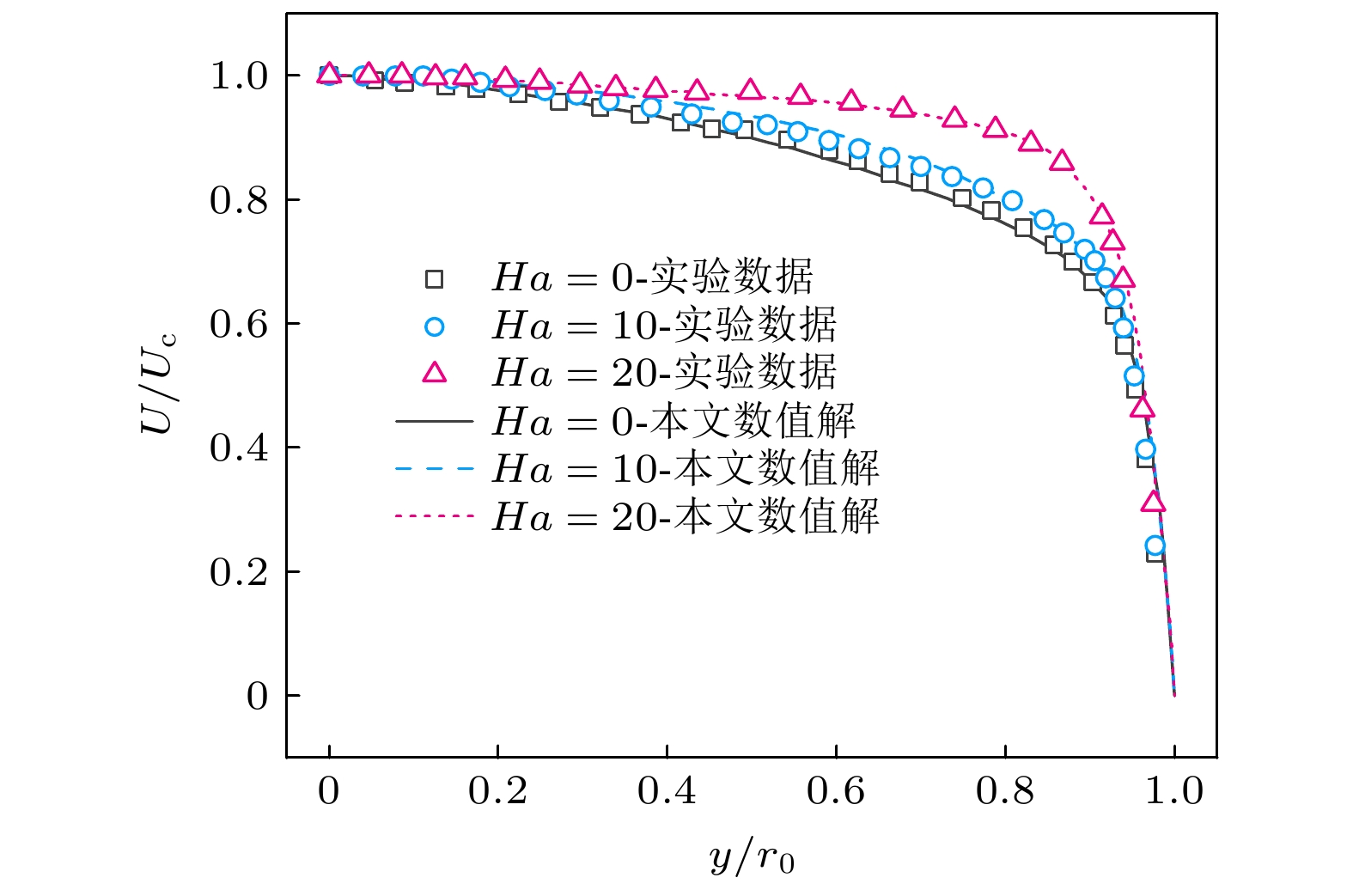
图 3 Re = 21375, Ha = 320, C = 0.0457时, 圆管yz截面上沿z = 0方向的流速数值解与文献[22]中实验数据的对比

Fig. 3. Comparison between the numerical solution of flow velocities along z = 0 direction on the yz cross-section of the circular tube and the experimental results in Ref. [22] under the condition of Re = 21375, Ha = 320, C = 0.0457.

下载: 全尺寸图片幻灯片

图 4 不同Re下圆管壁面处沿流动方向的努塞尔数数值解与Gnielinski经验解的对比

Fig. 4. Comparison between the numerical solution of Nusselt number along the flow direction at the wall of the circular tube under different Re and the Gnielinski empirical solution.

下载: 全尺寸图片幻灯片

图 5 不同Ha及不同C条件下圆管x = 200 mm截面上的速度幅值分布云图

Fig. 5. The contours of velocity amplitude distribution of the x = 200 mm cross-section of the circular tube under the conditions of different Ha and different C.

下载: 全尺寸图片幻灯片

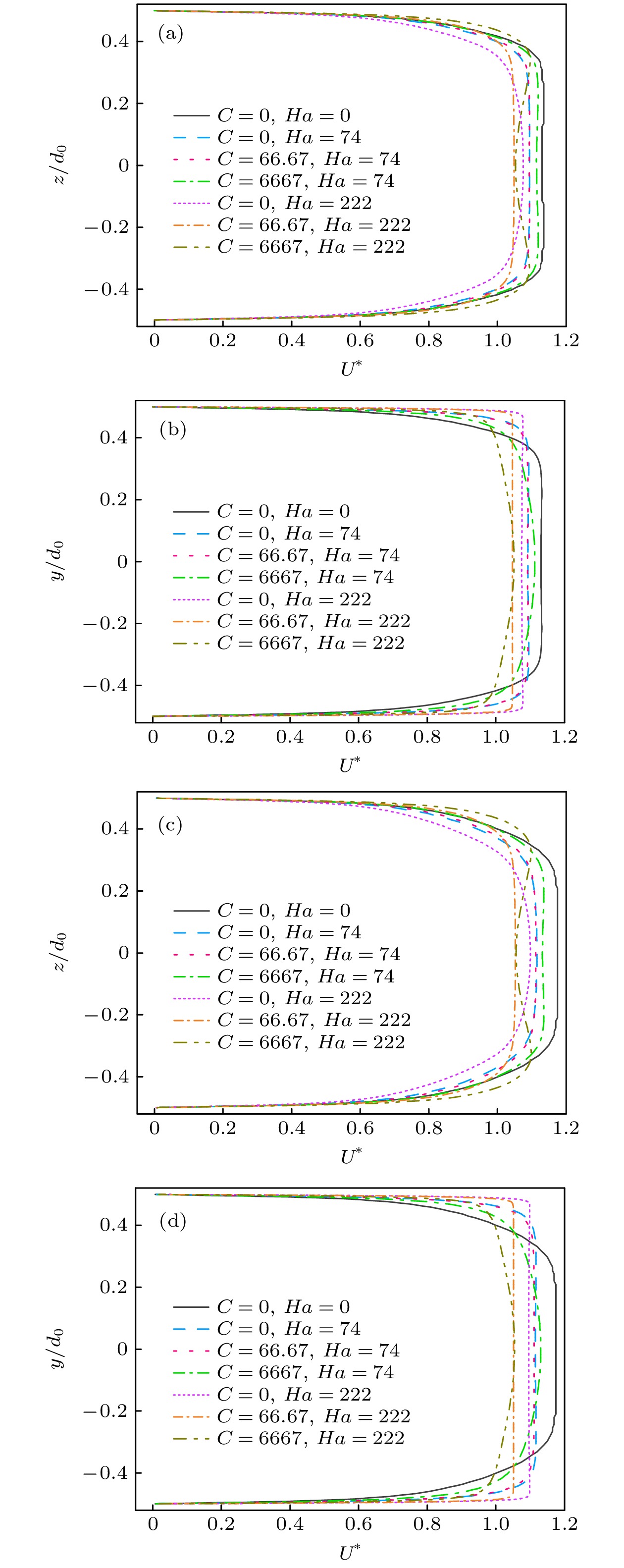
图 6 圆管x = 200 mm和x = 300 mm截面上y = 0沿线和z = 0沿线的无量纲速度分布曲线:　(a) x = 200 mm截面, y = 0; (b) x = 200 mm截面, z = 0; (c) x = 300 mm, y = 0; (d) x = 300 mm截面, z = 0

Fig. 6. The profiles of the dimensionless velocity distribution on the x = 200 mm and x = 300 mm cross-sections of the circular tube: (a) x = 200 mm cross-section, y = 0; (b) x = 200 mm cross-section, z = 0; (c) x = 300 mm cross-section, y = 0; (d) x = 300 mm cross-section, z = 0.

下载: 全尺寸图片幻灯片

图 7 不同Ha及不同C条件下圆管x = 200 mm截面上的湍流动能分布云图

Fig. 7. The contours of turbulent kinetic energy distribution of the x = 200 mm cross-section of the circular tube under the conditions of different Ha and different C.

下载: 全尺寸图片幻灯片

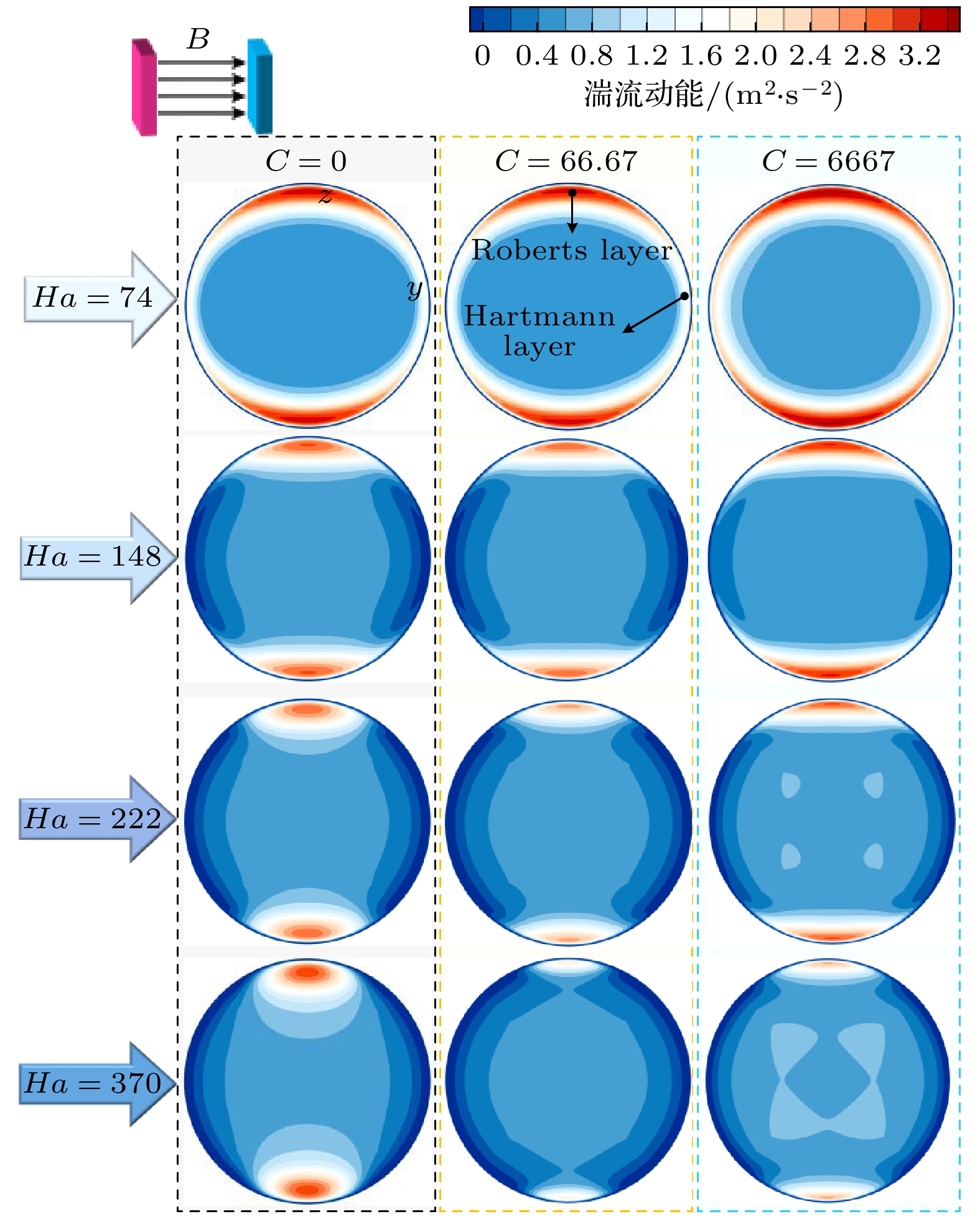
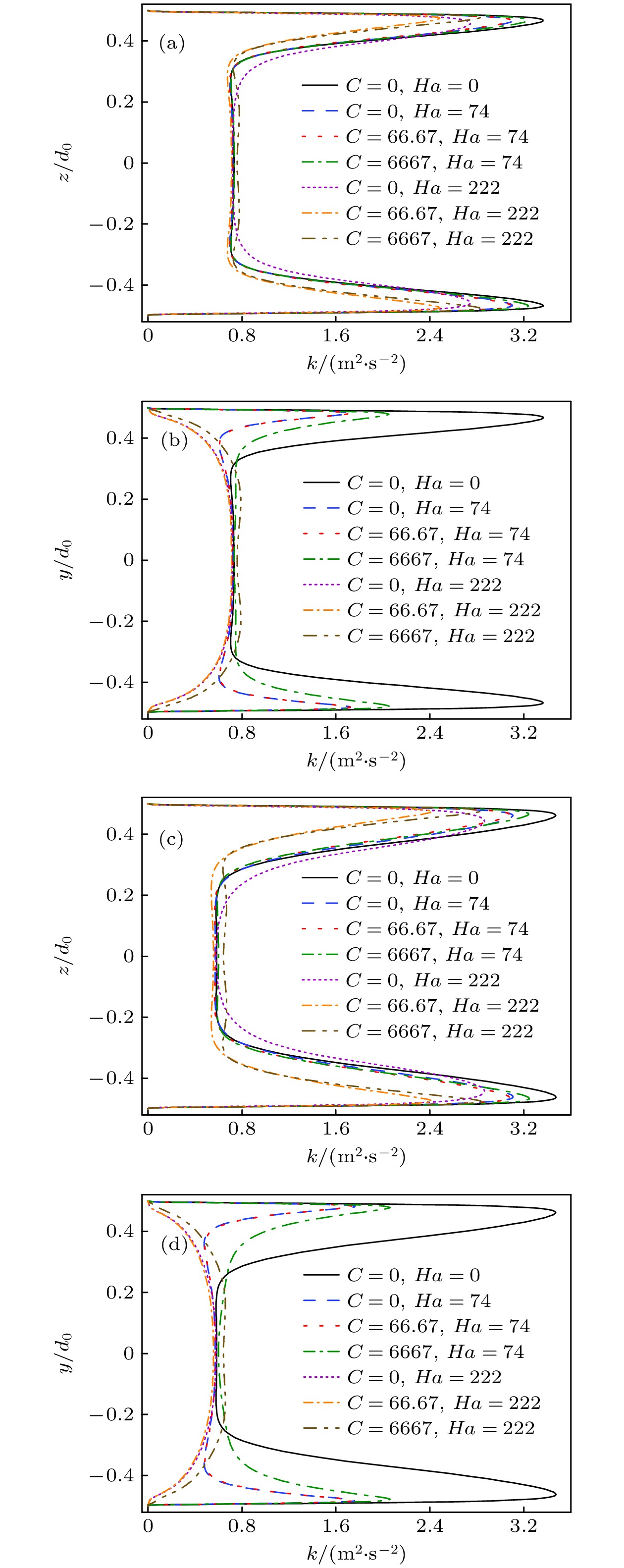
图 8 圆管x = 200 mm和x = 300 mm截面上y = 0沿线和z = 0沿线上的湍流动能分布曲线:　(a) x = 200 mm截面, y = 0 z; (b) x = 200 mm截面, z = 0; (c) x = 300 mm, y = 0; (d) x = 300 mm截面, z = 0

Fig. 8. The profiles of the turbulent kinetic energy distribution on the x = 200 mm and x = 300 mm cross-sections of the circular tube: (a) x = 200 mm cross-section, y = 0; (b) x = 200 mm cross-section, z = 0; (c) x = 300 mm cross-section, y = 0; (b) x = 300 mm cross-section, z = 0.

下载: 全尺寸图片幻灯片

图 9 不同Ha及不同C条件下圆管x = 300 mm截面上的温度分布云图

Fig. 9. The contours of temperature distribution of the x = 300 mm cross-section of the circular tube under the conditions of different Ha and different C.

下载: 全尺寸图片幻灯片

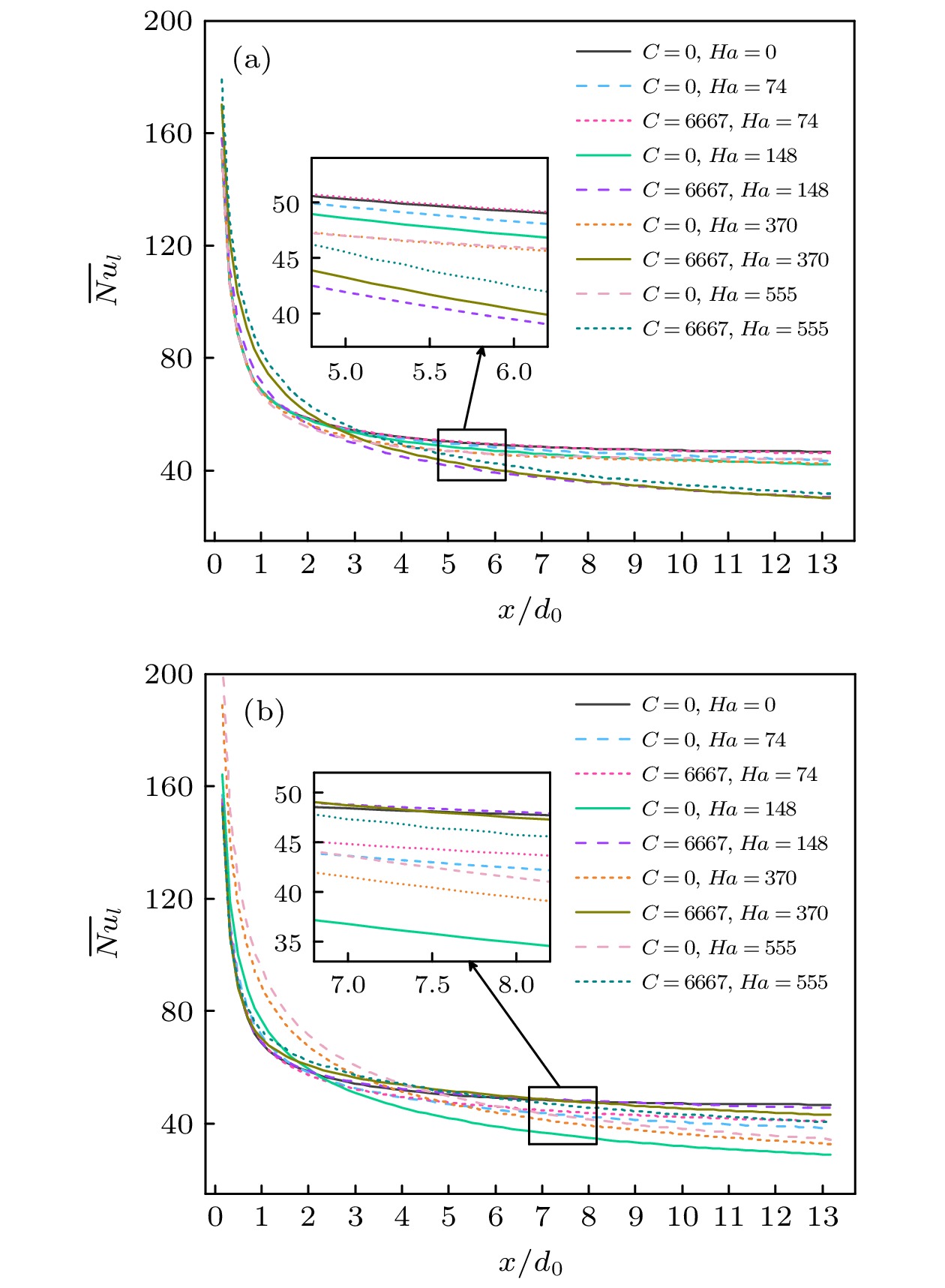
图 10 不同Ha下圆管y = 0, z = r₀壁面和z = 0, y = r₀壁面处沿x方向的局部努塞尔数分布曲线:　(a) y = 0, z = r_0, (b) z = 0, y = r₀

Fig. 10. The profiles of the local Nusselt number along the x direction at the wall of y = 0, z = r₀ and the wall of z = 0, y = r₀ of the circular tube under different Ha: (a) y = 0, z = r_0, (b) z = 0, y = r₀.

下载: 全尺寸图片幻灯片

图 11 不同C下圆管壁面处的平均努塞尔数$ \overline {Nu} $随Ha的变化

Fig. 11. Variation of the average Nusselt number $ \overline {Nu} $at the wall of circular tube with Ha under different C.

下载: 全尺寸图片幻灯片

图 12 Ha为74时不同C下圆管x = 200 mm截面上的感应电流分布:　(a) C = 0; (b) C = 66.67; (c) C = 6667

Fig. 12. Induced current distributions on the x = 200 mm cross-sections at different C when Ha is 74: (a) C = 0; (b) C = 66.67; (c) C = 6667.

下载: 全尺寸图片幻灯片

图 13 Ha为74时不同C下圆管x = 200 mm截面上的电磁力矢量:　(a) C = 0; (b) C = 66.67; (c) C = 6667

Fig. 13. Electromagnetic force vectors on the x = 200 mm cross-sections at different C when Ha is 74: (a) C = 0; (b) C = 66.67; (c) C = 6667.

下载: 全尺寸图片幻灯片

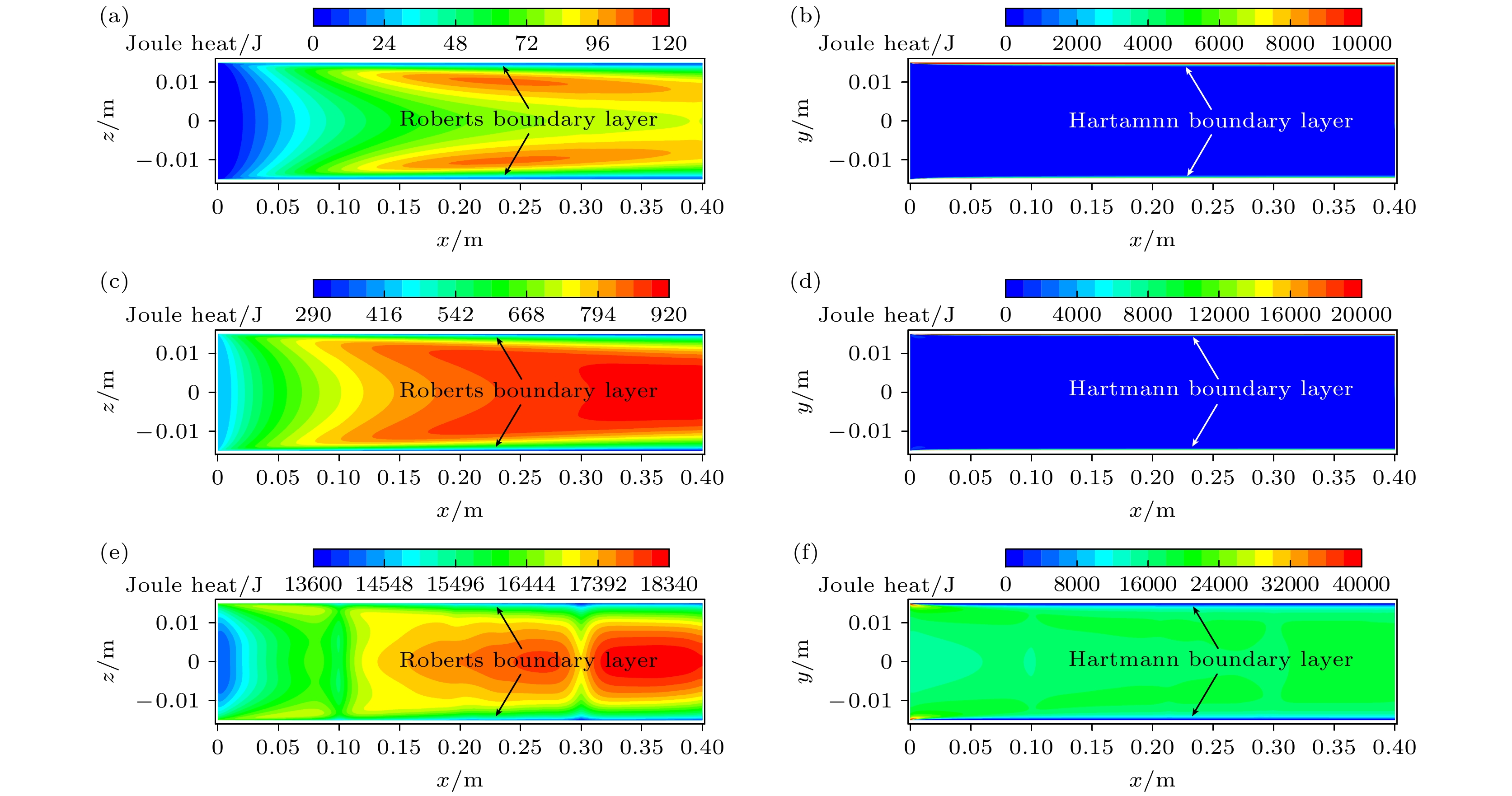
图 14 Ha为74时不同C下圆管y = 0截面和z = 0截面上的焦耳热分布:　(a) C = 0, y = 0截面; (b) C = 0, z = 0截面; (c) C = 66.67, y = 0截面; (d) C = 66.67, z = 0截面; (e) C = 6667, y = 0截面; (f) C = 6667, z = 0截面

Fig. 14. Joule heat distributions on the y = 0 mm cross-sections and the z = 0 mm cross-sections at different C when Ha is 74: (a) C = 0, y = 0 mm cross-section; (b) C = 0, z = 0 mm cross-section; (c) C = 66.67, y = 0 mm cross-section; (d) C = 66.67, z = 0 mm cross-section; (e) C = 6667, y = 0 mm cross-section; (f) C = 6667, z = 0 mm cross-section.

下载: 全尺寸图片幻灯片

表 1 不同网格尺寸设置及与之对应的努塞尔数计算结果和误差

Table 1. Different mesh size settings and the corresponding Nusselt number calculation results and errors.

网格编号	网格单元总数	壁面平均努塞尔数 $ \overline {Nu} $	努塞尔数误差 $\varepsilon {}_{\overline {Nu} }{\text{ = } }\left\| {1 - \overline {Nu} ({M_i})/\overline {Nu} ({M_6})} \right\|$
M1	1021557	45.4185	4.65%
M2	1740325	46.3474	2.70%
M3	2883249	46.7952	1.76%
M4	4202281	47.4477	0.39%
M5	5613165	47.5001	0.28%
M6	7484076	47.6335	—

下载: 导出CSV

map

[1]	Bedick C R, Woodside C R, Baylor R, Paul-Irudayaraj M 2020 Combust. Flame 213 140 Google Scholar
[2]	Zhao K, Lu Y, Li F, Hu J, Ming M, Wang X, Li S 2020 Acta Astronaut. 171 257 Google Scholar
[3]	Kim K S, Lee S H, Yun Y, Kwon S 2020 Acta Astronaut. 173 31 Google Scholar
[4]	Veefkind A 2004 IEEE T. Plasma Sci. 32 2197 Google Scholar
[5]	Wang Y, Ma T, Pei D, Chen C, Zhang D, Li C 2020 IEEE T. Plasma Sci. 48 1008 Google Scholar
[6]	李程, 毛保全, 白向华, 李晓刚 2018 兵工学报 39 851 Google Scholar Li C, Mao B Q, Bai X H, Li X G 2018 Acta Armam. 39 851 Google Scholar
[7]	成玉国, 夏广庆 2017 66 075204 Google Scholar Cheng Y G, Xia Y G 2017 Acta Phys. Sin. 66 075204 Google Scholar
[8]	Hedlund B, Houpt A, Gordeyev S, Leonov S 2018 AIAA J. 56 2699 Google Scholar
[9]	丁明松, 傅杨奥骁, 高铁锁, 董维中, 江涛, 刘庆宗 2020 69 214703 Google Scholar Ding M S, Fu Y A X, Gao T S, Dong W Z, Jiang T, Liu Q Z 2020 Acta Phys. Sin. 69 214703 Google Scholar
[10]	Mistrangelo C, Bühler L, Smolentsev S, Klüber V, Maione I, Aubert J 2021 Fusion Eng. Des. 173 112795 Google Scholar
[11]	Maurya A, Kumar R, Jha P K 2020 J. Manuf. Process. 60 596 Google Scholar
[12]	Yang R J, Hou H H, Wang Y N, Fu L M 2016 Sensor. Actuat. B-Chem. 224 1 Google Scholar
[13]	Moitoi A J, Shaw S 2022 Microvasc. Res. 139 104262 Google Scholar
[14]	Erdem M, Varol Y 2020 J. Therm. Anal. Calorim. 139 3897 Google Scholar
[15]	Krasnov D, Zikanov O, Boeck T 2012 J. Fluid Mech. 704 421 Google Scholar
[16]	Zikanov O, Krasnov D, Boeck T, Sukoriansky S 2019 J. Fluid Mech. 867 661 Google Scholar
[17]	Chatterjee D, Gupta S K J 2016 Appl. Fluid Mech. 9 2167 Google Scholar
[18]	Belyaev I, Sardov P, Melnikov I, Frick P 2021 Int. J. Therm. Sci. 161 106773 Google Scholar
[19]	Chaudhary R, Vanka S P, Thomas B G 2010 Phys. Fluids 22 075102 Google Scholar
[20]	Hunt J C R 1965 J. Fluid Mech. 21 577 Google Scholar
[21]	Tao Z, Ni M J 2015 Sci. China Phys. Mech. 58 024701
[22]	Zhang X, Pan C, Xu Z 2017 Fusion Eng. Des. 125 647 Google Scholar
[23]	Artemov V I, Makarov M V, Minko K B, Minko K B, Yankov G G 2020 Int. J. Heat Mass Tran. 146 118822 Google Scholar
[24]	Singh R J, Gohil T B 2019 Comput. Fluids 179 476 Google Scholar
[25]	Yarahmadi M, Goudarzi H M, Shafii M B 2015 Exp. Therm. Fluid Sci. 68 601 Google Scholar
[26]	Sha L, Ju Y, Zhang H, Wang J 2017 Appl. Therm. Eng 113 566 Google Scholar
[27]	Abadeh A, Sardarabadi M, Abedi M, Pourramezan M, Passandideh-Fard M, Maghrebi M 2020 J. Mol. Liq. 299 112206 Google Scholar
[28]	Shahsavar A, Saghafian M, Salimpour M R, Shafii M B 2016 Exp Therm. Fluid Sci. 76 1 Google Scholar
[29]	Afrand M, Karimipour A, Nadooshan A A, Akbari M 2016 Physica. E 84 474 Google Scholar
[30]	Khosravi A, Malekan M 2019 Eur. Phys. J. Plus 134 1 Google Scholar
[31]	Malekan M, Khosravi A 2018 Powder Techno. 333 364 Google Scholar
[32]	Hussam W K, Hamid A H A, Ng Z Y, Sheard G J 2018 Int. J. Therm. Sci. 134 453 Google Scholar
[33]	李开, 刘伟强 2016 65 064701 Google Scholar Li K, Liu W Q 2016 Acta Phys. Sin. 65 064701 Google Scholar
[34]	Liu Z, Li Y, Su Y 2018 Int. J. Adv. Manuf. Tech. 98 2015 Google Scholar
[35]	Tsilingiris P T 2008 Energ. Convers. Manage. 49 1098 Google Scholar
[36]	Stephan K, Laesecke A 1985 J. Phys. Chem. Ref. Data 14 227 Google Scholar
[37]	Menter F R 1994 AIAA J. 32 1598 Google Scholar
[38]	Widlund O, Zahrai S, Bark F H 1998 Phys. Fluids 10 1987 Google Scholar
[39]	Walker J S 1981 Journal de Mécanique 20 79
[40]	Takeuchi J, Satake S, Morley N B, Kunugi T, Yokomine T, Abdou, M A 2008 Fusion Eng. Des. 83 1082 Google Scholar
[41]	Gnielinski V 1976 Int. Chem. Eng 16 359
[42]	Bradshaw P 1974 Nature 249 135

[1]	邢赫威, 陈占秀, 杨历, 苏瑶, 李源华, 呼和仓. 不凝性气体对纳米通道内水分子流动传热影响的分子动力学模拟. , 2024, 73(9): 094701. doi: 10.7498/aps.73.20240192
[2]	李高芳, 殷文, 黄敬国, 崔昊杨, 叶焓静, 高艳卿, 黄志明, 褚君浩. 太赫兹时域光谱技术研究S掺杂GaSe晶体的电导率特性. , 2023, 72(4): 047801. doi: 10.7498/aps.72.20221548
[3]	赵晨蕊, 魏云昕, 刘婷婷, 秦明辉. 正弦微波磁场驱动亚铁磁畴壁动力学. , 2023, 72(20): 208502. doi: 10.7498/aps.72.20230913
[4]	刘联胜, 刘轩臣, 贾文琪, 田亮, 杨华, 段润泽. 小液滴撞击壁面传热特性数值分析. , 2021, 70(7): 074402. doi: 10.7498/aps.70.20201354
[5]	董帅, 纪祥勇, 李春曦. 横向磁场作用下Taylor-Couette湍流流动的大涡模拟. , 2021, 70(18): 184702. doi: 10.7498/aps.70.20210389
[6]	方芳, 鲍麟, 童秉纲. 基于斜驻点模型的剪切层撞击壁面流动及传热特性. , 2020, 69(21): 214401. doi: 10.7498/aps.69.20201000
[7]	陈建玲, 王辉, 贾焕玉, 马紫微, 李永宏, 谭俊. 超强磁场下中子星壳层的电导率和磁星环向磁场欧姆衰变. , 2019, 68(18): 180401. doi: 10.7498/aps.68.20190760
[8]	王胜, 徐进良, 张龙艳. 非对称纳米通道内流体流动与传热的分子动力学. , 2017, 66(20): 204704. doi: 10.7498/aps.66.204704
[9]	杜一帅, 康维, 郑瑞伦. 外延石墨烯电导率和费米速度随温度变化规律研究. , 2017, 66(1): 014701. doi: 10.7498/aps.66.014701
[10]	蔡继兴, 郭明, 渠旭, 李贺, 金光勇. 激光诱导等离子体的气体动力学和燃烧波扩展速度研究. , 2017, 66(9): 094202. doi: 10.7498/aps.66.094202
[11]	王松, 武占成, 唐小金, 孙永卫, 易忠. 聚酰亚胺电导率随温度和电场强度的变化规律. , 2016, 65(2): 025201. doi: 10.7498/aps.65.025201
[12]	邓新华, 刘江涛, 袁吉仁, 王同标. 全新的电导率特征矩阵方法及其在石墨烯THz频率光学特性上的应用. , 2015, 64(5): 057801. doi: 10.7498/aps.64.057801
[13]	张程宾, 许兆林, 陈永平. 粗糙纳通道内流体流动与传热的分子动力学模拟研究. , 2014, 63(21): 214706. doi: 10.7498/aps.63.214706
[14]	范喆, 马晓萍, 李尚赫, 沈帝虎, 朴红光, 金东炫. 消磁场对纳米铁磁线磁畴壁动力学行为的影响. , 2012, 61(10): 107502. doi: 10.7498/aps.61.107502
[15]	薛春霞, 张善元, 树学锋. 横向磁场中大挠度金属薄板的混沌振动. , 2010, 59(9): 6599-6605. doi: 10.7498/aps.59.6599
[16]	张玉萍, 张会云, 耿优福, 谭晓玲, 姚建铨. 太赫兹波在有限电导率金属空芯波导中的传输特性. , 2009, 58(10): 7030-7033. doi: 10.7498/aps.58.7030
[17]	蔡建臻, 朱宏伟, 吴德海, 刘峰, 吕力. 单壁碳纳米管微分电导在高压和强磁场下的实验研究. , 2006, 55(12): 6585-6588. doi: 10.7498/aps.55.6585
[18]	魏兵, 葛德彪. 各向异性有耗介质板介电系数和电导率的反演. , 2005, 54(2): 648-652. doi: 10.7498/aps.54.648
[19]	苏昉, 谢斌, 赵明文, 吴希俊. 纳米CaF2离子电导率和介电常数的静水压效应. , 1995, 44(5): 755-762. doi: 10.7498/aps.44.755
[20]	方道腴. 在横向磁场中真空电弧后退速度和阴极温度的关系. , 1983, 32(7): 838-844. doi: 10.7498/aps.32.838

计量

文章访问数: 4269
PDF下载量: 71
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板