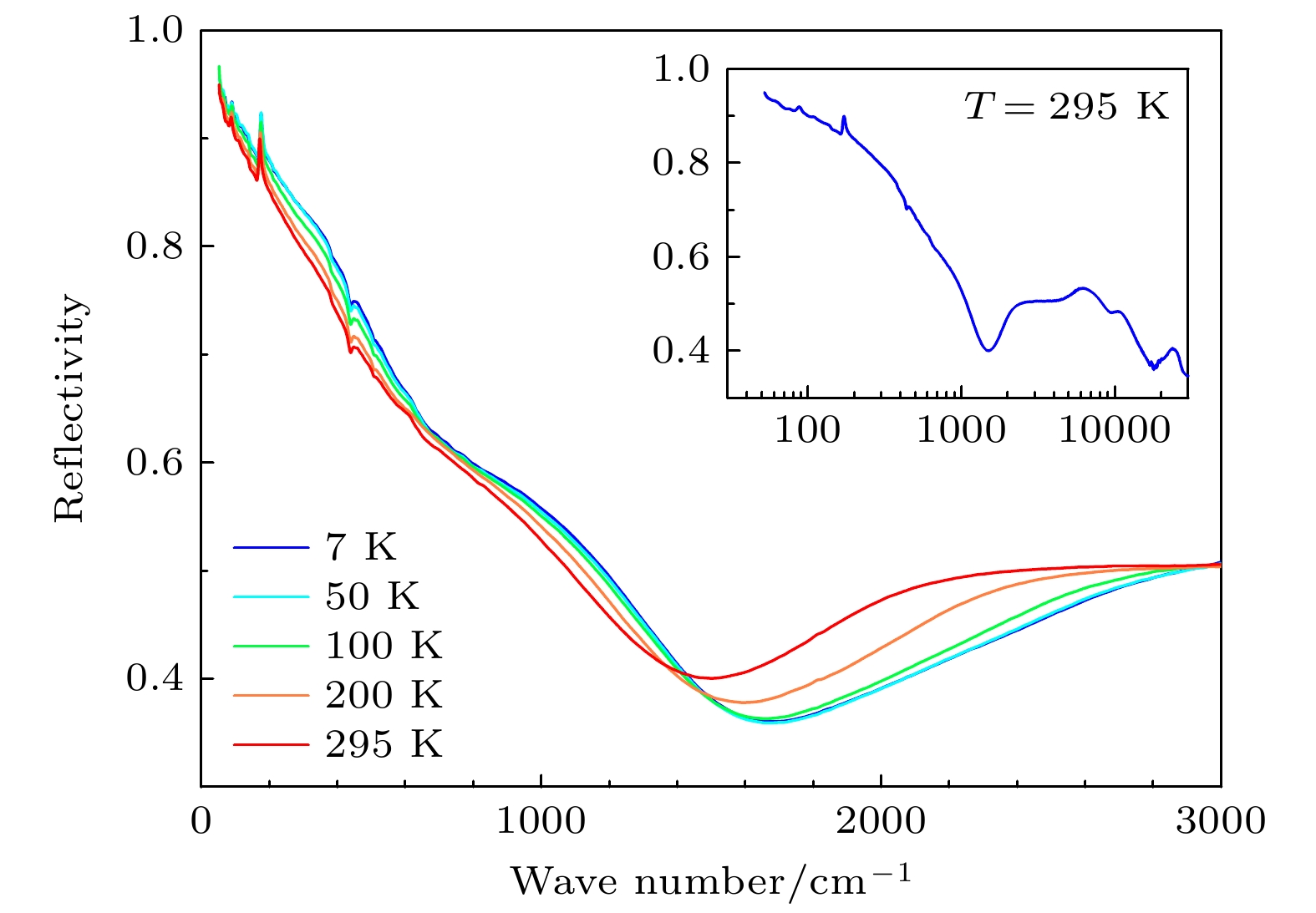
-
对于新型拓扑材料BaMnSb2, 研究了从7 K到常温下温度依赖的宽频红外光谱特性. 随着温度的降低, 绝对反射谱中等离子体极小值有着明显的蓝移, 表明载流子浓度存在随温度变化的行为. 在光电导谱的实部中存在两段随着频率线性增加的响应, 它们的线性外延不经过原点, 表明BaMnSb2的费米能级附近有打开能隙的Dirac型色散. 此外, 在低温下还发现了一段不随频率变化的光电导, 且无法用传统的Drude-Lorentz模型拟合. 因此本文引入了一个恒定的光电导分量, 得到了满意的拟合结果. 通过计算和分析, 我们认为恒定光电导分量可能来自于拓扑材料BaMnSb2的表面态响应.A detailed infrared optical spectrum of the new topological material BaMnSb2 has been measured at temperatures ranging from 7 K to 295 K. As the temperature decreases, the plasma minimum has a clear blue shift in reflectivity spectrum, indicating that the carrier density changes with temperature. In the real part of the optical conductivity
$\sigma_{1}(\omega)$ , two linearly-increased components can be identified, but neither of their extrapolation pass through the origin, which proves that BaMnSb2 has a gapped Dirac dispersion near the Fermi level. Comparing with the theoretical calculation by using first-principles methods, the onset of these two linearly-increased components are in good agreement with the band structures. In addition, a range of constant optical conductivity is found in$\sigma_{1}(\omega)$ , which cannot be described well by the Drude-Lorentz model. Therefore, we introduce a frequency-independent component to fit$\sigma_{1}(\omega)$ successfully. However, different from the Dirac nodal-line semimetal YbMnSb2 which shares same fitting results as well as crystal structure, the constant component in BaMnSb2 has a small proportion of$\sigma_{1}(\omega)$ . Through calculation and analysis, we attribute the constant component to the surface state of BaMnSb2.[1] Dziawa P, Kowalski B J, Dybko K, Buczko R, Szczerbakow A, Szot M, Lusakowska E, Balasubra- manian T, Wojek B M, Berntsen M H 2012 Nat. Mater. 11 1023
Google Scholar
[2] Zhang H, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438
Google Scholar
[3] Wang Z J, Sun Y, Chen X Q, Franchini C, Xu G, Weng H M, Dai X, Fang Z 2012 Phys. Rev. B 85 195320
Google Scholar
[4] Ma X M, Zhao Y, Zhang K, Kumar S, Lu R, Li J, Yao Q, Shao J, Hou F, Wu X 2021 Phys. Rev. B 103 121112
Google Scholar
[5] de Boer J C, Wielens D H, Voerman J A, de Ronde B, Huang Y, Golden M S, Li C, Brinkman A 2019 Phys. Rev. B 99 085124
Google Scholar
[6] Hsieh D, Xia Y, Qian D, Wray L, Meier F, Dil J H, Osterwalder J, Patthey L, Fedorov A V, Lin H 2009 Phys. Rev. Lett. 103 146401
Google Scholar
[7] Su Y H, Shi W, Felser C, Sun Y 2018 Phys. Rev. B 97 155431
Google Scholar
[8] Singh S, Garcia-Castro A C, Valencia-Jaime I, Munoz F, Romero A H 2016 Phys. Rev. B 94 161116
Google Scholar
[9] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[10] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[11] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[12] Park J, Lee G, Wolff-Fabris F, Koh Y Y, Eom M J, Kim Y K, Farhan M A, Jo Y J, Kim C, Shim J H 2011 Phys. Rev. Lett. 107 126402
Google Scholar
[13] Wang K F, Graf D, Wang L M, Lei H C, Tozer S W, Petrovic C 2012 Phys. Rev. B 85 041101
[14] Li L J, Wang K F, Graf D, Wang L M, Wang A F, Petrovic C 2016 Phys. Rev. B 93 115141
Google Scholar
[15] Wang A F, Zaliznyak I, Ren W J, Wu L J, Graf D, Garlea V O, Warren J B, Bozin E, Zhu Y M, Petrovic C 2016 Phys. Rev. B 94 165161
Google Scholar
[16] Wang K F, Graf D, Lei H C, Tozer S W, Petrovic C 2011 Phys. Rev. B 84 220401
Google Scholar
[17] May A F, McGuire M A, Sales B C 2014 Phys. Rev. B 90 075109
Google Scholar
[18] Chinotti M, Pal A, Ren W J, Petrovic C, Degiorgi L 2016 Phys. Rev. B 94 245101
Google Scholar
[19] Lee G, Farhan M A, Kim J S, Shim J H 2013 Phys. Rev. B 87 245104
Google Scholar
[20] Liu J, Hu J, Cao H, Zhu Y, Chuang A, Graf D, Adams D J, Radmanesh S M A, Spinu L, Chiorescu I 2016 Sci. Rep. 6 30525
Google Scholar
[21] Chaudhuri D, Cheng B, Yaresko A, Gibson Q D, Cava R J, Armitage N P 2017 Phys. Rev. B 96 075151
Google Scholar
[22] Qiu Z Y, Le C C, Dai Y M, Xu B, He J B, Yang R, Chen G F, Hu J P, Qiu X G 2018 Phys. Rev. B 98 115151
Google Scholar
[23] Kealhofer R, Jang S, Griffin S M, John C, Benavides K A, Doyle S, Helm T, Moll P J W, Neaton J B, Chan J Y 2018 Phys. Rev. B 97 045109
Google Scholar
[24] Wang Y Y, Xu S, Sun L L, Xia T L 2018 Phys. Rev. Mater. 2 021201
Google Scholar
[25] Qiu Z Y, Le C C, Liao Z Y, Xu B, Yang R, Hu J P, Dai Y M, Qiu X G 2019 Phys. Rev. B 100 125136
Google Scholar
[26] Qiu Z Y, Liao Z Y, Qiu X G 2019 Chin. Phys. B 28 047801
Google Scholar
[27] Farhan M A, Lee G, Shim J H 2014 J. Phys. Condens. Matter 26 042201
Google Scholar
[28] Rong H T, Zhou L Q, He J B, Song C Y, Xu Y, Cai Y Q, Li C, Wang Q Y, Zhao L, Liu G D, Xu Z Y, Chen G F, Weng H M, Zhou X J 2021 Chin. Phys. B 30 067403
Google Scholar
[29] Armitage N P, Mele E J, Vishwanath A 2018 Rev. Mod. Phys. 90
[30] Carbotte J P 2017 J. Phys. Condens. Matter 29 045301
Google Scholar
[31] Hosur P, Parameswaran S A, Vishwanath A 2012 Phys. Rev. Lett. 108 046602
Google Scholar
[32] Schilling M B, Schoop L M, Lotsch B V, Dressel M, Pronin A V 2017 Phys. Rev. Lett. 119 187401
Google Scholar
[33] Topp A, Queiroz R, Grüneis A, Müchler L, Rost A W, Varykhalov A, Marchenko D, Krivenkov M, Rodolakis F, McChesney J L 2017 Phys. Rev. X 7 041073
[34] Chen R Y, Zhang S J, Zhang M Y, Dong T, Wang N L 2017 Phys. Rev. Lett. 118 107402
Google Scholar
[35] Shao Y, Sun Z, Wang Y, Xu C, Sankar R, Breindel A J, Cao C, Fogler M M, Millis A J, Chou F 2019 Proc. Natl. Acad. Sci. 11v 1168
[36] Homes C C, Reedyk M, Cradles D A, Timusk T 1993 Appl. Opt. 32 2976
Google Scholar
[37] Li B W, Jiang W C, Chen G Y, Xiang Y, Xie W, Dai Y M, Zhu X Y, Yang H, Wen H H 2020 Sci. China-Phys. Mech. Astron. 63 117011
Google Scholar
[38] Kuzmenko A B, van Heumen E, Carbone F, van der Marel D 2008 Phys. Rev. Lett. 100 117401
Google Scholar
[39] Mak K F, Sfeir M Y, Wu Y, Lui C H, Misewich J A, Heinz T F 2008 Phys. Rev. Lett. 101 196405
Google Scholar
[40] Ando T, Zheng Y, Suzuura H 2002 J. Phys. Soc. Jpn. 71 1318
Google Scholar
[41] Habe T, Koshino M 2018 Phys. Rev. B 98 125201
Google Scholar
-
图 1 BaMnSb2在5个温度点50—3000 cm–1范围内的反射率. 插图为室温下到30000 cm–1的反射谱
Fig. 1. Reflectivity of BaMnSb2 at five representative temperatures between 50–3000 cm–1. The inset displays the reflectivity up to 30000 cm–1 at room temperature
图 2 通过Kramers-Kronig计算得到相应的光电导的实部. 插图为室温下到更高频率的光电导谱
Fig. 2. The corresponding real part of optical conductivity
$ \sigma_{1}(\omega) $ is calculated through Kramers-Kronig transformation. The inset shows$ \sigma_{1}(\omega) $ over a broad frequency range at room temperature
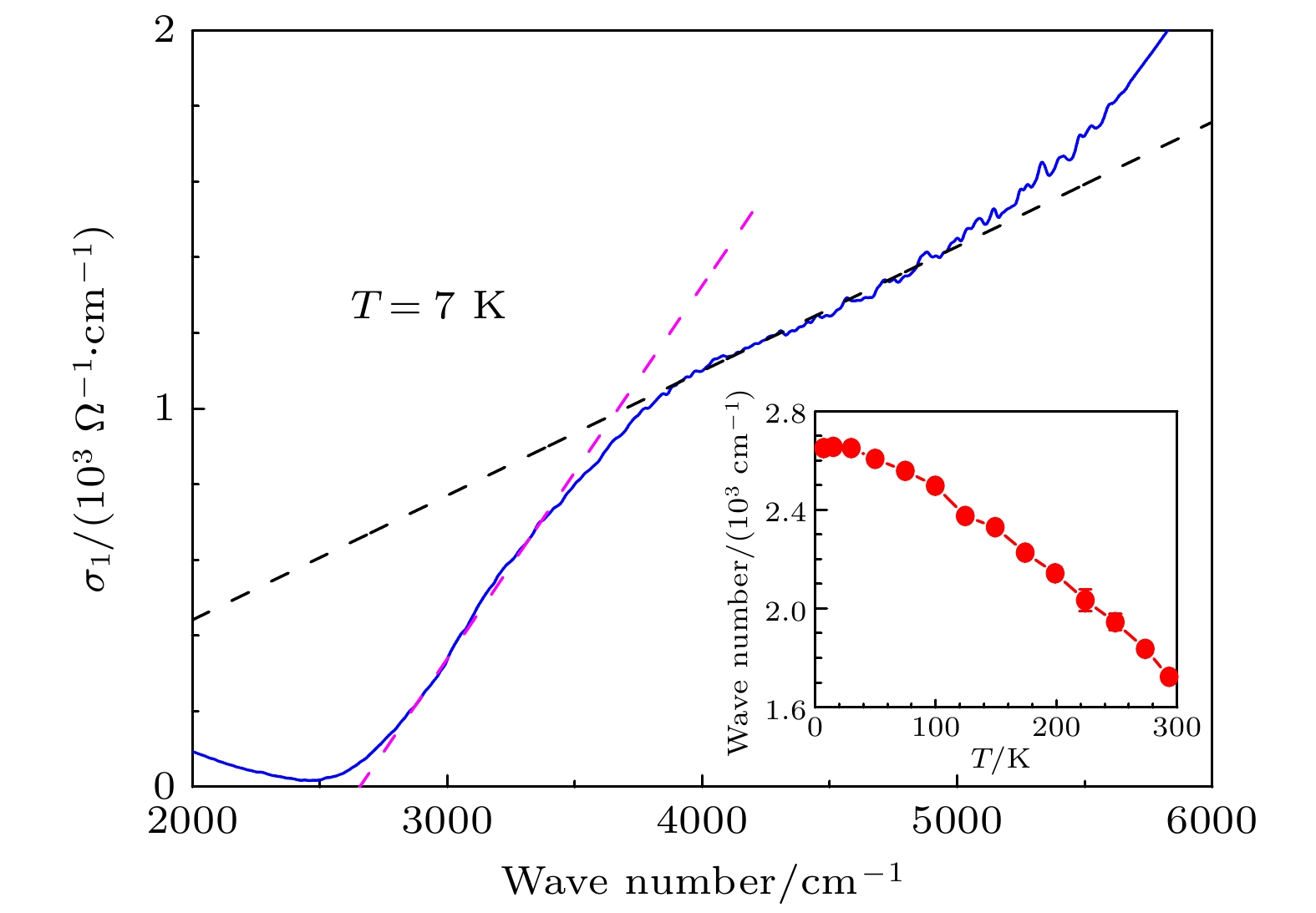
图 3 蓝色实线为7 K时BaMnSb2在高频波段的光电导谱, 粉色虚线和黑色虚线分别示意了两段线性增加的光电导. 插图是不同温度下粉色虚线线性外延与横坐标的交点, 对应了Dirac能隙随温度变化的关系
Fig. 3. The blue solid curve is
$ \sigma_{1}(\omega) $ for BaMnSb2 at 7 K in high-frequency range. The pink and dark dashed lines denote two range of linearly-increased$ \sigma_{1}(\omega) $ . The inset exhibits extrapolation of the pink dashed line to zero conductivity at finite frequency, corresponding to the temperature-dependent Dirac gap
图 4 BaMnSb2在7 K时的
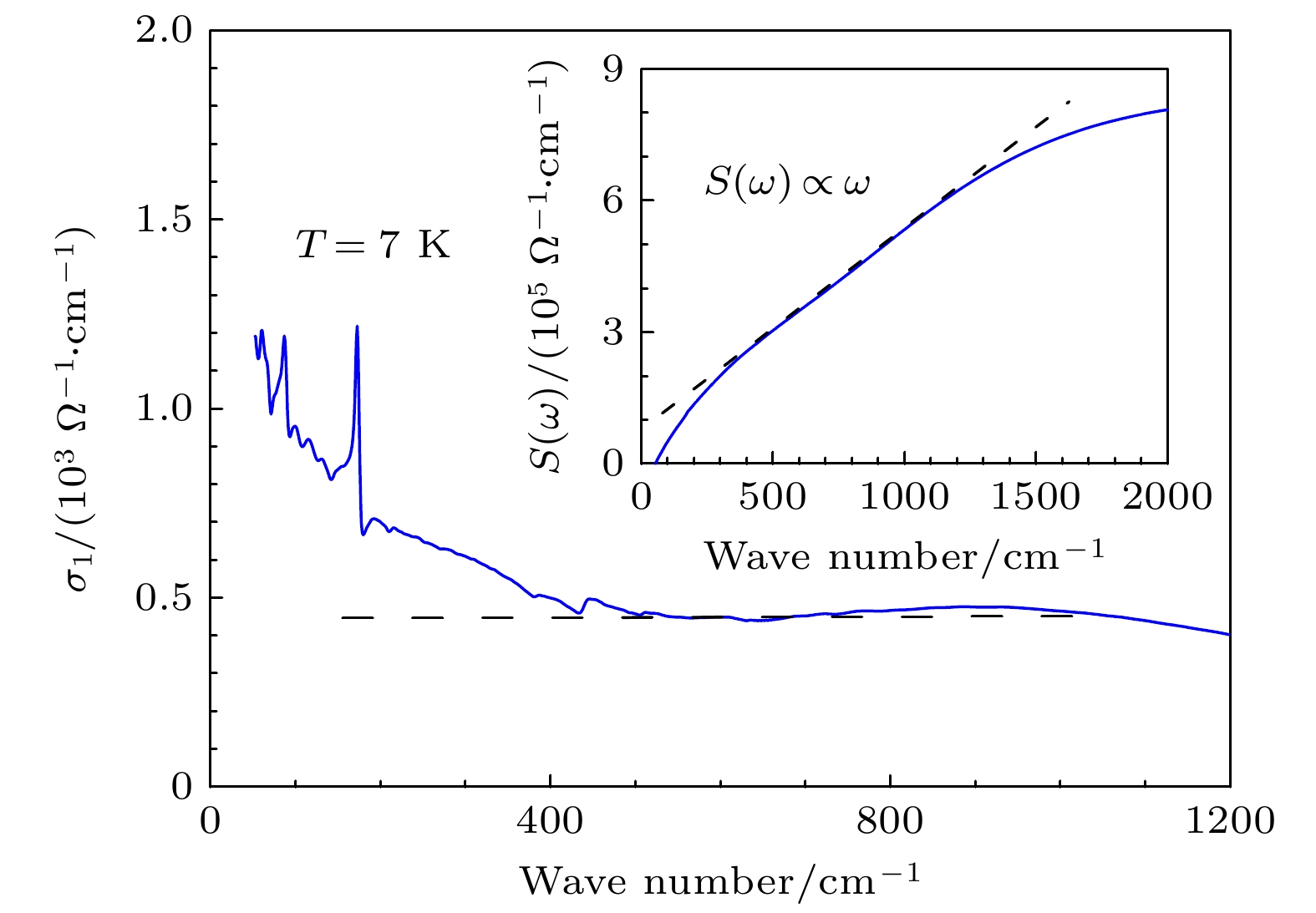
$ \sigma_{1}(\omega) $ , 其中黑色虚线注明了恒定光电导组分. 插图为$ \sigma_{1}(\omega) $ 的谱重随频率变化的关系, 其中黑色虚线表明在350—1150 cm–1范围内谱重随频率线性增加Fig. 4.
$ \sigma_{1}(\omega) $ for BaMnSb2 at 7 K. The dark dashed line denotes the frequency-independent component. The inset portrays the spectral weight$ S(\omega) $ at 7 K, and the dark dashed line represents$ S(\omega) $ follows an ω behavior in the range between 350–1150 cm–1
图 5
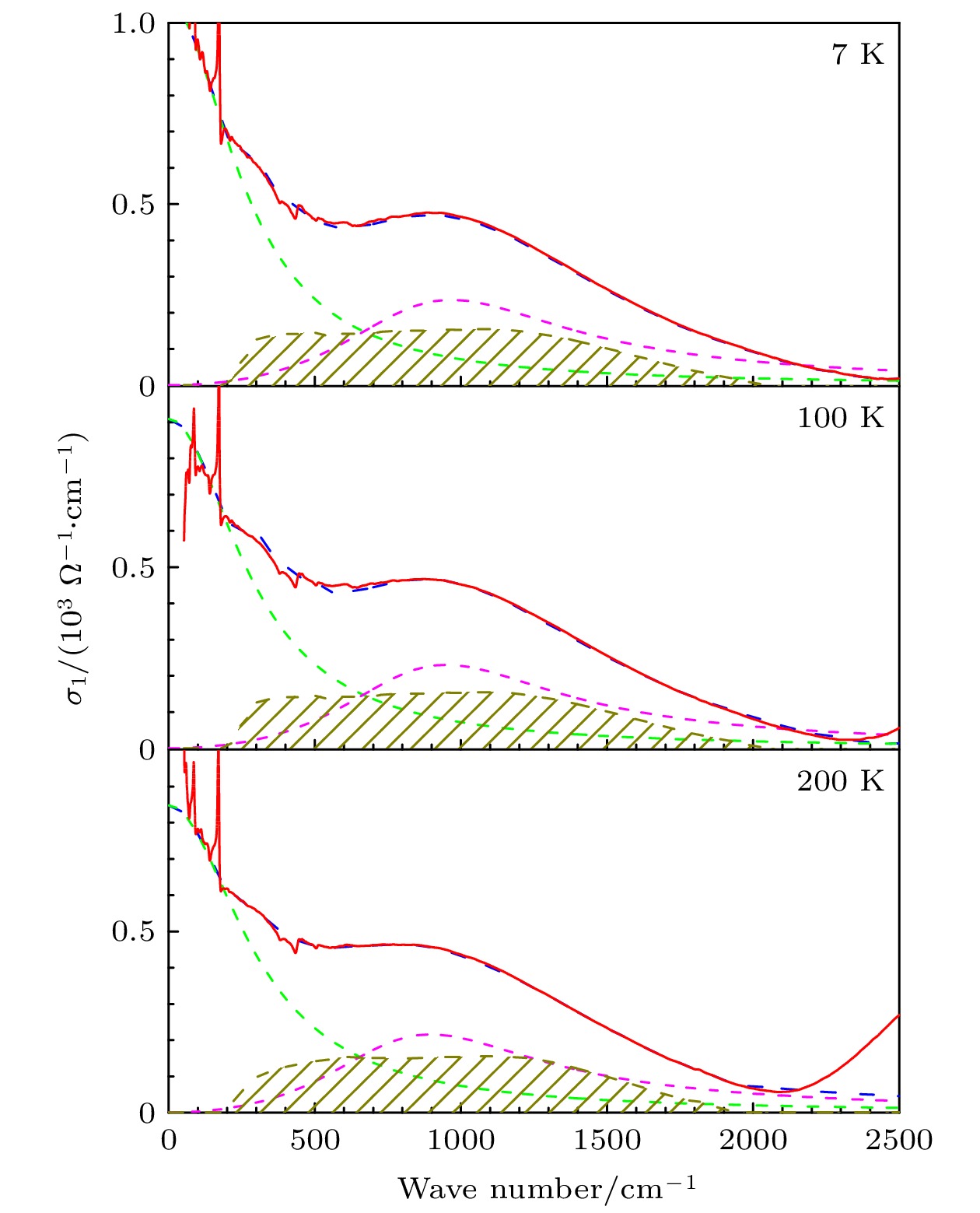
$ \sigma_{1}(\omega) $ 在0—2500 cm–1范围内的拟合结果, 拟合的组分为一个绿色的Drude 分量, 一个粉色的Lorentz分量, 和一个深黄色的恒定分量. 对于100和200 cm–1附近的红外活性声子暂不讨论Fig. 5. Fitting results for
$ \sigma_{1}(\omega) $ in 0–2500 cm–1 frequency range, which is decomposed into one Drude term (green dashed line), one Lorentz term (pink dashed line), and a constant component (dark yellow dashed line). The infrared-active phonons near 100 and 200 cm–1 are ignored -
[1] Dziawa P, Kowalski B J, Dybko K, Buczko R, Szczerbakow A, Szot M, Lusakowska E, Balasubra- manian T, Wojek B M, Berntsen M H 2012 Nat. Mater. 11 1023
Google Scholar
[2] Zhang H, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438
Google Scholar
[3] Wang Z J, Sun Y, Chen X Q, Franchini C, Xu G, Weng H M, Dai X, Fang Z 2012 Phys. Rev. B 85 195320
Google Scholar
[4] Ma X M, Zhao Y, Zhang K, Kumar S, Lu R, Li J, Yao Q, Shao J, Hou F, Wu X 2021 Phys. Rev. B 103 121112
Google Scholar
[5] de Boer J C, Wielens D H, Voerman J A, de Ronde B, Huang Y, Golden M S, Li C, Brinkman A 2019 Phys. Rev. B 99 085124
Google Scholar
[6] Hsieh D, Xia Y, Qian D, Wray L, Meier F, Dil J H, Osterwalder J, Patthey L, Fedorov A V, Lin H 2009 Phys. Rev. Lett. 103 146401
Google Scholar
[7] Su Y H, Shi W, Felser C, Sun Y 2018 Phys. Rev. B 97 155431
Google Scholar
[8] Singh S, Garcia-Castro A C, Valencia-Jaime I, Munoz F, Romero A H 2016 Phys. Rev. B 94 161116
Google Scholar
[9] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[10] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[11] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[12] Park J, Lee G, Wolff-Fabris F, Koh Y Y, Eom M J, Kim Y K, Farhan M A, Jo Y J, Kim C, Shim J H 2011 Phys. Rev. Lett. 107 126402
Google Scholar
[13] Wang K F, Graf D, Wang L M, Lei H C, Tozer S W, Petrovic C 2012 Phys. Rev. B 85 041101
[14] Li L J, Wang K F, Graf D, Wang L M, Wang A F, Petrovic C 2016 Phys. Rev. B 93 115141
Google Scholar
[15] Wang A F, Zaliznyak I, Ren W J, Wu L J, Graf D, Garlea V O, Warren J B, Bozin E, Zhu Y M, Petrovic C 2016 Phys. Rev. B 94 165161
Google Scholar
[16] Wang K F, Graf D, Lei H C, Tozer S W, Petrovic C 2011 Phys. Rev. B 84 220401
Google Scholar
[17] May A F, McGuire M A, Sales B C 2014 Phys. Rev. B 90 075109
Google Scholar
[18] Chinotti M, Pal A, Ren W J, Petrovic C, Degiorgi L 2016 Phys. Rev. B 94 245101
Google Scholar
[19] Lee G, Farhan M A, Kim J S, Shim J H 2013 Phys. Rev. B 87 245104
Google Scholar
[20] Liu J, Hu J, Cao H, Zhu Y, Chuang A, Graf D, Adams D J, Radmanesh S M A, Spinu L, Chiorescu I 2016 Sci. Rep. 6 30525
Google Scholar
[21] Chaudhuri D, Cheng B, Yaresko A, Gibson Q D, Cava R J, Armitage N P 2017 Phys. Rev. B 96 075151
Google Scholar
[22] Qiu Z Y, Le C C, Dai Y M, Xu B, He J B, Yang R, Chen G F, Hu J P, Qiu X G 2018 Phys. Rev. B 98 115151
Google Scholar
[23] Kealhofer R, Jang S, Griffin S M, John C, Benavides K A, Doyle S, Helm T, Moll P J W, Neaton J B, Chan J Y 2018 Phys. Rev. B 97 045109
Google Scholar
[24] Wang Y Y, Xu S, Sun L L, Xia T L 2018 Phys. Rev. Mater. 2 021201
Google Scholar
[25] Qiu Z Y, Le C C, Liao Z Y, Xu B, Yang R, Hu J P, Dai Y M, Qiu X G 2019 Phys. Rev. B 100 125136
Google Scholar
[26] Qiu Z Y, Liao Z Y, Qiu X G 2019 Chin. Phys. B 28 047801
Google Scholar
[27] Farhan M A, Lee G, Shim J H 2014 J. Phys. Condens. Matter 26 042201
Google Scholar
[28] Rong H T, Zhou L Q, He J B, Song C Y, Xu Y, Cai Y Q, Li C, Wang Q Y, Zhao L, Liu G D, Xu Z Y, Chen G F, Weng H M, Zhou X J 2021 Chin. Phys. B 30 067403
Google Scholar
[29] Armitage N P, Mele E J, Vishwanath A 2018 Rev. Mod. Phys. 90
[30] Carbotte J P 2017 J. Phys. Condens. Matter 29 045301
Google Scholar
[31] Hosur P, Parameswaran S A, Vishwanath A 2012 Phys. Rev. Lett. 108 046602
Google Scholar
[32] Schilling M B, Schoop L M, Lotsch B V, Dressel M, Pronin A V 2017 Phys. Rev. Lett. 119 187401
Google Scholar
[33] Topp A, Queiroz R, Grüneis A, Müchler L, Rost A W, Varykhalov A, Marchenko D, Krivenkov M, Rodolakis F, McChesney J L 2017 Phys. Rev. X 7 041073
[34] Chen R Y, Zhang S J, Zhang M Y, Dong T, Wang N L 2017 Phys. Rev. Lett. 118 107402
Google Scholar
[35] Shao Y, Sun Z, Wang Y, Xu C, Sankar R, Breindel A J, Cao C, Fogler M M, Millis A J, Chou F 2019 Proc. Natl. Acad. Sci. 11v 1168
[36] Homes C C, Reedyk M, Cradles D A, Timusk T 1993 Appl. Opt. 32 2976
Google Scholar
[37] Li B W, Jiang W C, Chen G Y, Xiang Y, Xie W, Dai Y M, Zhu X Y, Yang H, Wen H H 2020 Sci. China-Phys. Mech. Astron. 63 117011
Google Scholar
[38] Kuzmenko A B, van Heumen E, Carbone F, van der Marel D 2008 Phys. Rev. Lett. 100 117401
Google Scholar
[39] Mak K F, Sfeir M Y, Wu Y, Lui C H, Misewich J A, Heinz T F 2008 Phys. Rev. Lett. 101 196405
Google Scholar
[40] Ando T, Zheng Y, Suzuura H 2002 J. Phys. Soc. Jpn. 71 1318
Google Scholar
[41] Habe T, Koshino M 2018 Phys. Rev. B 98 125201
Google Scholar
下载:
计量
- 文章访问数: 3925
- PDF下载量: 109
- 被引次数: 0
