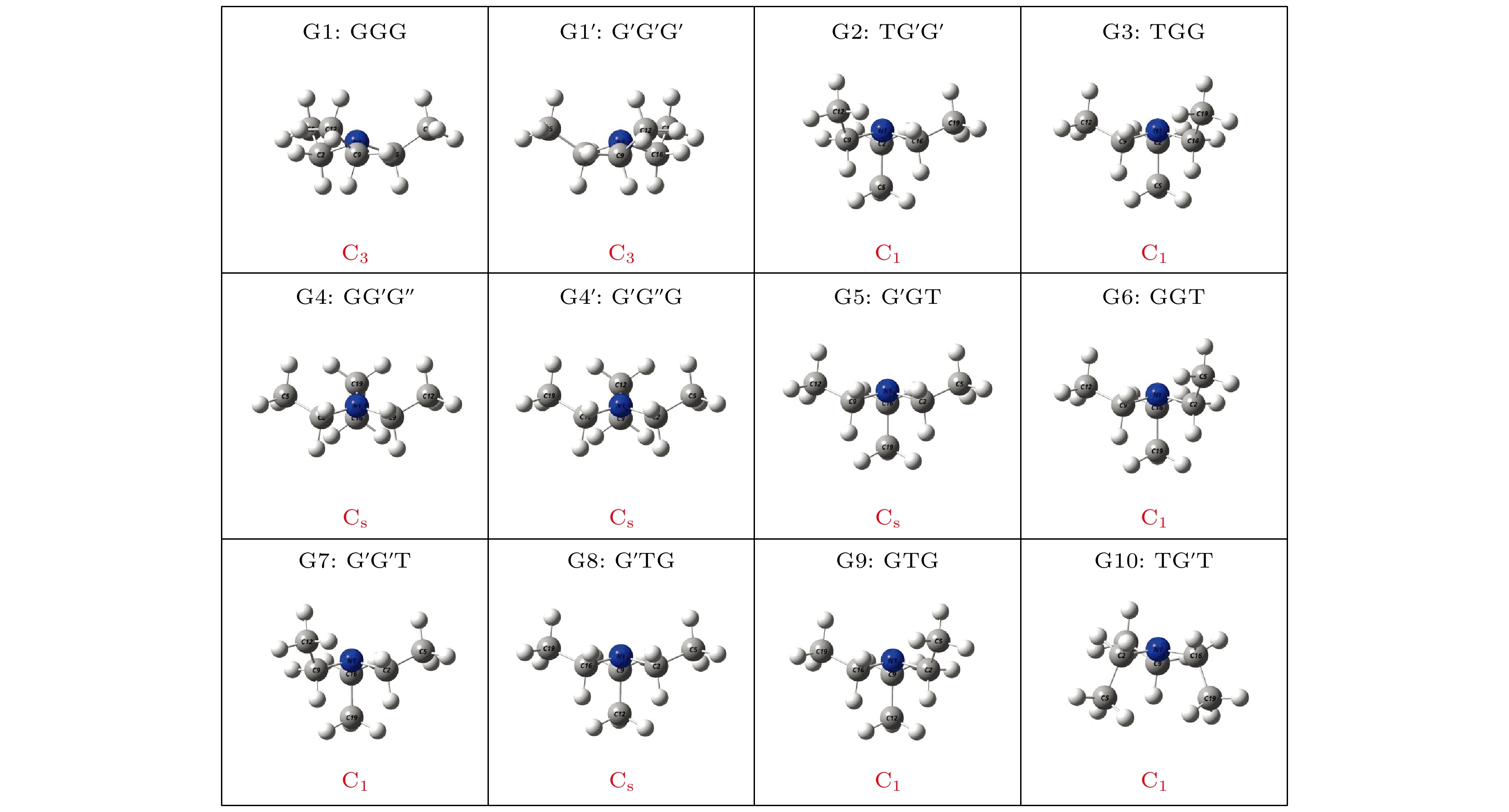
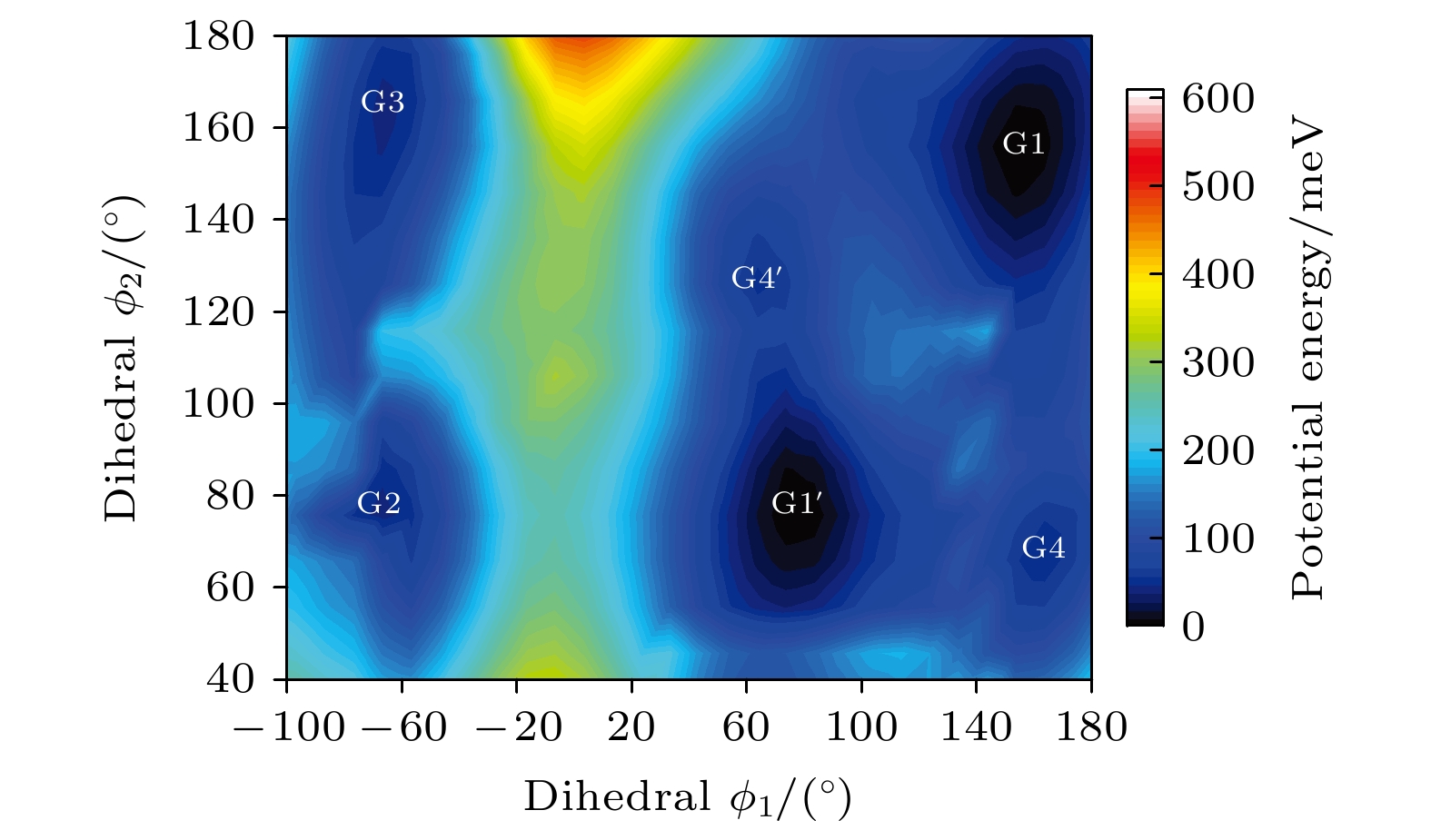
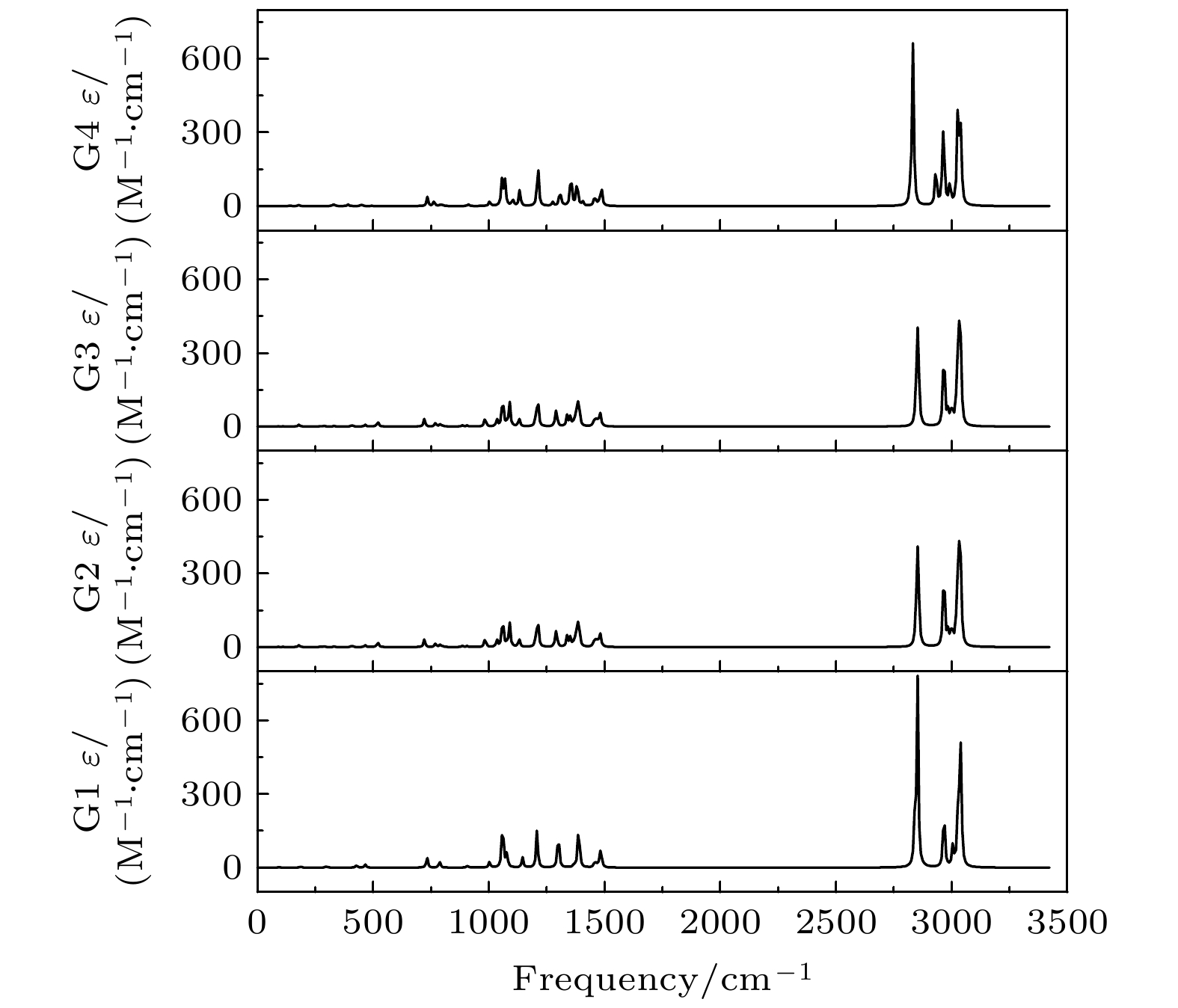
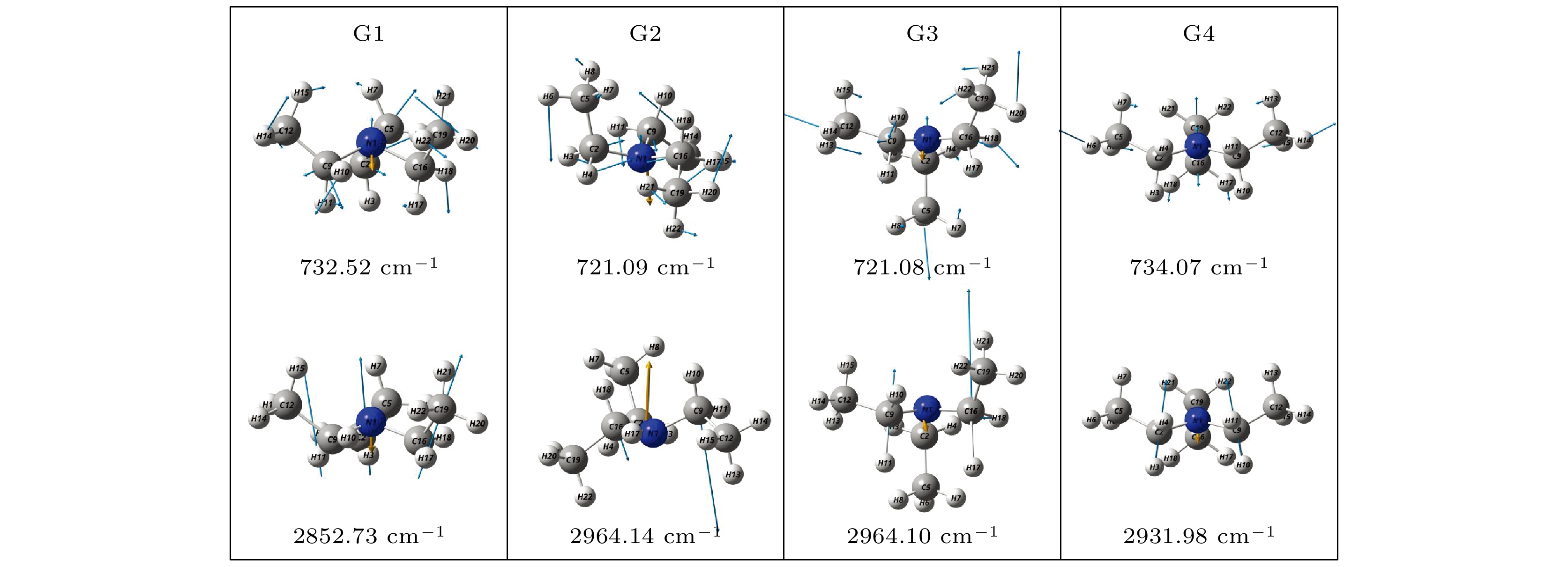
-
利用密度泛函理论B3LYP的方法, 在6-311++G(d, p)基组水平上沿二面角ϕ1(C9N1C2C5)和ϕ2(C16N1C9C12)构成的二维坐标下扫描了–180°—180°范围内构象异构化势能面, 甄别出12种三乙胺基态异构体. 进一步辅以二阶微扰理论MP2的方法, 在相同基组水平下计算与优化6种能量较低的构象异构体的结构与能量. 结果表明具有C3对称性的G1与G1'是最稳定构象, 并识别出两种具有新的甲基取向的G4与G4'构象异构体. 另外, 通过G1—G4红外光谱与振动模式的比较, 分析了它们之间的相似性与差异性. G1—G4的红外谱线显示在0—1600 cm–1范围内的强度较弱, 而在2800—3300 cm–1范围内的强度较强, 标定出伞状振动与C—H伸缩振动等特征振动模, 不同构象所引起的红外谱峰的平均移动量小于20 cm–1.
Based on the method of density functional theory B3LYP with a 6-311++G(d, p) basis set, the potential energy surface of conformational isomerization along the two-dimensional coordinates formed by the dihedral angles ϕ1(C9N1C2C5) and ϕ2(C16N1C9C12) in a range of –180°–180° is investigated. And 12 ground state conformers of triethylamine are identified. Furthermore,with the second-order Moller-Plesset perturbation theory MP2 on the same basis set level, the structures of six lower-energy conformers are optimized and their energy values are estimated. The results show that G1 and G1' with C3 symmetry are the most stable conformers and G4 and G4' with new methyl orientations are identified. In addition, some vibrational modes in the infrared spectra of G1–G4 are assigned and discussed. The infrared spectra of G1–G4 show that the intensity is weak in a range of 0–1600 cm–1, while the intensity is strong in a range of 2800–3300 cm–1. The characteristic vibration modes such as umbrella vibration and CH stretching vibration are assigned. The average shift of the corresponding infrared peaks on different conformations is estimated at less than 20 cm–1. -
Keywords:
- conformation isomerization /
- density-functional theory calculation /
- potential energy surface /
- infrared spectra
[1] Park S T, Kim S K, Kim M S 2002 Nature 415 306
Google Scholar
[2] Kim M H, Shen L, Tao H, Martinez T J, Suits A G 2007 Science 315 1561
Google Scholar
[3] Gosselin J L, Weber P M 2005 J. Phys. Chem. A 109 4899
Google Scholar
[4] Deb S, Bayes B A, Minitti M P, Weber P M 2011 J. Phys. Chem. A 115 1804
Google Scholar
[5] Minitti M P, Weber P M 2007 Phys. Rev. Lett. 98 253004
Google Scholar
[6] Kuthirummal N, Weber P M 2003 Chem. Phys. Lett. 378 647
Google Scholar
[7] Kuthirummal N, Weber P M 2006 J. Mol. Struct. 787 163
Google Scholar
[8] Dian B C, Clarkson J R, Zwier T S 2004 Science 303 1169
Google Scholar
[9] Kumar K 1971 Chem. Phys. Lett. 9 504
Google Scholar
[10] Crocker C, Goggin P L 1978 J. Chem. Soc. Dalton Trans 388
[11] Bushweller C H, Fleischman S H, Grady G L, McGoff P, Rithner C D, Whalon M R, Brennan J G, Marcantonio R P, Domingue R P 1982 J. Am. Chem. Soc. 104 6224
Google Scholar
[12] Fleischman S H, Weltin E E, Bushweller C H 1985 J. Comput. Chem. 6 249
Google Scholar
[13] Takeuchi H, Kojima T, Egawa T, Konaka S 1992 J. Phys. Chem. 96 4389
Google Scholar
[14] Grimme S 2011 Wiley Interdiscip. Rev. -Comput. Mol. Sci. 1 211
Google Scholar
[15] Grimme S, Hansen A, Brandenburg J G, Bannwarth C 2016 Chem. Rev. 116 5105
Google Scholar
[16] Sølling T I, Kötting C, Zewail A H 2003 J. Phys. Chem. A 107 10872
Google Scholar
[17] Cardoza J D, Rudakov F M, Weber P M 2008 J. Phys. Chem. A 112 10736
Google Scholar
[18] Deb S, Cheng X, Weber P M 2013 J. Phys. Chem. Lett. 4 2780
Google Scholar
[19] Cheng X, Zhang Y, Deb S, Minitti M P, Gao Y, Jónsson H, Weber P M 2014 Chem. Sci. 5 4394
Google Scholar
[20] Frisch M J, Trucks G W, Schlegel H B, Scuseria G E, Robb M A, Cheeseman J R, Scalmani G, Barone V, Mennucci B, Petersson G A, Nakatsuji H, Caricato M, Li X, Hratchian H P, Izmaylov A F, Bloino J, Zheng G, Sonnenberg J L, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery J A Jr, Peralta J E, Ogliaro F, Bearpark M, Heyd J J, Brothers E, Kudin K N, Staroverov V N, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant J C, Iyengar S S, Tomasi J, Cossi M, Rega N, Millam J M, Klene M, Knox J E, Cross J B, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann R E, Yazyev O, Austin A J, Cammi R, Pomelli C, Ochterski J W, Martin R L, Morokuma K, Zakrzewski V G, Voth G A, Salvador P, Dannenberg J J, Dapprich S, Daniels A D, Farkas Ö, Foresman J B, Ortiz J V, Cioslowski J, Fox D J 2009 Gaussian09 (Revision E.01)
[21] Vosko S H, Wilk L, Nusair M 1980 Can. J. Phys. 58 1200
Google Scholar
[22] Krishnan R, Binkley J S, Seeger R, Pople J A 1980 J. Chem. Phys. 72 650
Google Scholar
[23] Møller C, Plesset M S 1934 Phys. Rev. 46 618
Google Scholar
-
图 1 三乙胺分子在笛卡尔坐标系下的结构示意图.
Fig. 1. Schematic structure of triethylamine in Cartesian coordinate system.
图 2 沿二面角ϕ1(C9N1C2C5)与ϕ2(C16N1C9C12)构成的二维坐标扫描–180°—180°范围内三乙胺构象异构化势能面
Fig. 2. The conformational isomerization potential energy surface in the range of –180°–180° scanning along the two-dimensional coordinates formed by the dihedral angles of ϕ1 (C9N1C2C5) and ϕ2 (C16N1C9C12).
图 3 基于B3LYP/6-311++G(d, p)水平计算得到的三乙胺的12种稳定构象异构体的分子结构
Fig. 3. The 12 stable conformers of triethylamine calculated on B3LYP/6-311++G(d, p) level.
图 4 ϕ1 (–100°—180°)与ϕ2 (40°—180°)范围内的6种构象异构体的势能面
Fig. 4. The conformational isomerization potential energy surface of the six conformers in ϕ1(–100°–180°) and ϕ2 (40°–180°).
图 5 在B3LYP/6-311++G(d, p)水平上计算得到的G1—G4构象异构体的红外光谱
Fig. 5. The infrared spectra of the G1–G4 conformers calculated at B3LYP/6-311++G(d, p) level.
图 6 基于B3LYP/6-311++G(d, p)水平计算得到的G1—G4构象异构体的伞形振动(上排图)和C—H对称伸缩振动(下排图)及其频率
Fig. 6. The umbrella vibration mode (upper panel) and C—H symmetric stretch mode (lower panel) and their frequencies of the G1—G4 conformers calculated on B3LYP/6-311++G(d, p) level.
表 1 基于B3LYP/6-311++G(d, p)水平计算得到的三乙胺的12种稳定构象异构体的二面角与能量
Table 1. The energies and dihedral angles of the 12 conformers of triethylamine calculated on B3LYP/6-311++G(d, p) level
Conformers ϕ1/(°) ϕ2/(°) ϕ3/(°) Energy/Hartree Relative E/meV G1 (GGG) 155.42 155.60 155.64 –292.501669 0 G1' (G'G'G') 77.67 77.63 77.63 –292.501620 1.33 G2 (TG'G') –66.62 76.02 63.21 –292.500061 43.76 G3 (TGG) –64.76 165.17 151.59 –292.500061 43.76 G4 (GG'G'') 162.85 67.24 115.28 –292.499824 50.21 G4' (G'G''G) 67.24 115.26 162.86 –292.499824 50.21 G5 (G'GT) –167.71 –60.28 65.25 –292.499826 50.15 G6 (GGT) –75.99 –63.21 66.63 –292.500061 43.76 G7 (G'G'T) –165.17 –151.59 64.75 –292.500061 43.76 G8 (G'TG) 60.28 –65.24 167.73 –292.499826 50.15 G9 (GTG) 151.58 –64.74 165.19 –292.500061 43.76 G10 (TG'T) 56.64 –156.48 76.67 –292.497311 118.59 
下载: 导出CSV
表 2 三乙胺的6种稳定构象异构体在MP2/6-311++G(d, p)计算下的二面角与能量
Table 2. The energies and dihedral angles of the six stable conformers of triethylamine on the level of MP2/6-311++G(d, p)
Conformers ϕ1/(°) ϕ2/(°) ϕ3/(°) Energy/Hartree Relative E/meV G1 (GGG) 157.62 157.63 157.63 –291.559737 0 G1' (G'G'G') 79.53 79.53 79.53 –291.559737 0 G2 (TG'G') –66.91 75.27 57.80 –291.558559 32.06 G3 (TGG) –59.62 175.87 158.42 –291.558563 31.95 G4 (GG'G'') 166.11 67.66 117.32 –291.558516 33.23 G4' (G'G''G) 67.74 117.11 166.19 –291.558517 33.20
下载: 导出CSV
表 3 基于B3LYP/6-311++G(d, p)水平计算得到的G1—G4构象异构体的振动模式与频率
Table 3. The vibrational modes and their frequencies of the G1-G4 conformers calculated on B3LYP/6-311++G(d, p) level
Modes Frequency /cm–1 Infrared /(arb. units) G1 G2 G3 G4 G1 G2 G3 G4 ν1 87.22 55.02 55.10 50.35 0.1532 0.0639 0.0639 0.0004 ν2 90.98 87.43 87.41 96.49 0.1978 0.1857 0.1857 0.0238 ν3 95.03 109.27 109.28 140.35 0.1084 0.2932 0.2933 0.7795 ν4 188.06 178.51 178.54 178.16 1.1011 2.0829 2.0830 1.1365 ν5 208.61 203.62 203.58 205.94 0.0793 0.0717 0.0724 0.0393 ν6 214.02 224.68 224.73 223.87 0.0468 0.0690 0.0687 0.1212 ν7 294.38 268.43 268.36 256.33 1.0986 0.3758 0.3757 0.1000 ν8 304.06 290.93 290.98 328.65 0.3330 1.0227 1.0225 1.6826 ν9 305.06 331.61 331.61 332.28 0.3301 0.6897 0.6908 0.3791 ν10 427.73 407.68 407.74 390.84 3.0184 1.9295 1.9286 1.8981 ν11 465.12 465.26 465.28 449.38 1.9245 2.3956 2.3948 1.6278 ν12 466.51 519.32 519.35 495.27 1.9272 6.0474 6.0464 0.2229 ν13 732.52 721.09 721.08 734.07 12.9402 9.4813 9.4797 10.9942 ν14 786.67 769.53 769.53 763.17 3.8307 4.3371 4.3412 6.1536 ν15 787.30 788.70 788.71 790.73 3.8921 2.6364 2.6346 1.2979 ν16 797.88 799.48 799.50 799.56 0.0602 1.6382 1.6374 1.5619 ν17 907.63 886.81 886.80 911.00 1.2513 1.6792 1.6806 1.3188 ν18 907.82 906.38 906.37 911.59 1.2450 1.3085 1.3102 0.5529 ν19 1002.59 983.42 983.41 1003.17 6.7677 11.0738 11.0739 5.7366 ν20 1059.24 1035.02 1035.00 1056.02 29.6466 8.2727 8.2697 18.7155 ν21 1059.73 1059.50 1059.46 1058.63 30.0288 30.8396 31.1034 16.0090 ν22 1065.72 1062.07 1062.06 1069.23 3.2100 8.4580 8.2166 30.8172 ν23 1078.10 1078.78 1078.77 1076.49 8.5384 3.6151 3.6028 1.3100 ν24 1078.68 1090.02 1090.04 1102.40 8.3190 28.7911 28.7831 8.1051 ν25 1145.20 1130.09 1130.09 1132.97 12.0682 10.1819 10.1824 19.8481 ν26 1208.09 1204.99 1204.96 1210.21 23.0883 18.4553 18.4412 17.6571 ν27 1208.58 1213.11 1213.11 1213.26 23.1735 25.1079 25.1196 35.4460 ν28 1295.98 1286.87 1286.86 1275.96 6.1543 5.5069 5.5346 4.4355 ν29 1299.90 1291.74 1291.73 1307.05 19.8870 19.0478 19.0085 20.9498 ν30 1301.08 1338.30 1338.29 1319.27 19.5949 13.3278 13.3106 1.2005 ν31 1368.21 1352.09 1352.09 1354.63 1.9917 11.3690 11.3924 37.8361 ν32 1369.16 1366.65 1366.64 1357.26 1.2772 3.0836 3.0821 5.3537 ν33 1377.64 1375.36 1375.35 1377.69 0.3191 3.9451 3.9459 0.5963 ν34 1388.04 1377.00 1377.00 1381.06 17.8509 14.4179 14.4269 19.6423 ν35 1388.15 1386.56 1386.55 1382.64 18.3740 20.6580 20.6282 12.8529 ν36 1388.87 1390.27 1390.26 1404.98 19.7944 15.6998 15.6974 5.4524 ν37 1457.17 1452.04 1452.05 1453.70 2.7473 4.8488 4.8565 5.2712 ν38 1457.42 1458.81 1458.81 1455.34 1.6935 4.5549 4.5301 0.3420 ν39 1457.69 1461.08 1461.08 1458.89 2.2572 2.7707 2.7867 3.6730 ν40 1462.71 1465.68 1465.67 1462.41 1.8527 2.0538 2.0584 4.0415 ν41 1470.31 1469.26 1469.25 1465.41 1.2048 3.4122 3.4014 0.0857 ν42 1470.92 1470.19 1470.18 1473.12 1.5336 1.3596 1.3783 3.1465 ν43 1480.41 1477.89 1477.88 1478.47 7.1590 2.9233 2.9249 1.5156 ν44 1481.40 1480.62 1480.60 1484.66 7.0152 14.8916 14.8851 10.1121 ν45 1485.83 1490.87 1490.86 1487.68 12.4306 1.4478 1.4478 14.3785 ν46 2840.18 2846.52 2846.55 2823.87 23.2447 36.5331 36.7500 30.6694 ν47 2840.74 2855.55 2855.62 2833.67 23.3082 133.4917 133.2390 190.3336 ν48 2852.73 2964.14 2964.10 2931.98 238.2268 28.9250 28.9420 52.7107 ν49 2966.71 2965.86 2965.83 2961.43 29.7433 22.5935 22.5842 24.4676 ν50 2967.27 2967.80 2967.77 2962.15 29.7303 26.9332 26.9495 32.0017 ν51 2967.73 2969.71 2969.69 2966.69 20.4277 26.6680 26.6499 55.0959 ν52 3005.55 2985.78 2985.82 2967.51 12.9188 19.0174 18.9607 9.9999 ν53 3006.00 2999.96 2999.91 2982.63 12.0858 16.2484 16.2880 1.3433 ν54 3009.33 3003.92 3003.90 2993.29 0.0669 7.0967 7.1223 29.3355 ν55 3025.88 3022.39 3022.35 3025.08 9.0331 39.4849 39.4879 51.7362 ν56 3028.87 3026.72 3026.71 3026.92 48.6932 15.0249 15.0950 24.4990 ν57 3029.12 3029.64 3029.64 3028.60 44.4949 61.7552 61.8929 54.1919 ν58 3037.74 3031.73 3031.72 3036.45 53.6899 42.2463 42.0251 3.3194 ν59 3039.70 3037.26 3037.24 3037.37 45.2729 52.3351 52.2987 69.7071 ν60 3040.26 3040.20 3040.20 3041.40 46.0316 44.4987 44.5093 31.7214
下载: 导出CSV
-
[1] Park S T, Kim S K, Kim M S 2002 Nature 415 306
Google Scholar
[2] Kim M H, Shen L, Tao H, Martinez T J, Suits A G 2007 Science 315 1561
Google Scholar
[3] Gosselin J L, Weber P M 2005 J. Phys. Chem. A 109 4899
Google Scholar
[4] Deb S, Bayes B A, Minitti M P, Weber P M 2011 J. Phys. Chem. A 115 1804
Google Scholar
[5] Minitti M P, Weber P M 2007 Phys. Rev. Lett. 98 253004
Google Scholar
[6] Kuthirummal N, Weber P M 2003 Chem. Phys. Lett. 378 647
Google Scholar
[7] Kuthirummal N, Weber P M 2006 J. Mol. Struct. 787 163
Google Scholar
[8] Dian B C, Clarkson J R, Zwier T S 2004 Science 303 1169
Google Scholar
[9] Kumar K 1971 Chem. Phys. Lett. 9 504
Google Scholar
[10] Crocker C, Goggin P L 1978 J. Chem. Soc. Dalton Trans 388
[11] Bushweller C H, Fleischman S H, Grady G L, McGoff P, Rithner C D, Whalon M R, Brennan J G, Marcantonio R P, Domingue R P 1982 J. Am. Chem. Soc. 104 6224
Google Scholar
[12] Fleischman S H, Weltin E E, Bushweller C H 1985 J. Comput. Chem. 6 249
Google Scholar
[13] Takeuchi H, Kojima T, Egawa T, Konaka S 1992 J. Phys. Chem. 96 4389
Google Scholar
[14] Grimme S 2011 Wiley Interdiscip. Rev. -Comput. Mol. Sci. 1 211
Google Scholar
[15] Grimme S, Hansen A, Brandenburg J G, Bannwarth C 2016 Chem. Rev. 116 5105
Google Scholar
[16] Sølling T I, Kötting C, Zewail A H 2003 J. Phys. Chem. A 107 10872
Google Scholar
[17] Cardoza J D, Rudakov F M, Weber P M 2008 J. Phys. Chem. A 112 10736
Google Scholar
[18] Deb S, Cheng X, Weber P M 2013 J. Phys. Chem. Lett. 4 2780
Google Scholar
[19] Cheng X, Zhang Y, Deb S, Minitti M P, Gao Y, Jónsson H, Weber P M 2014 Chem. Sci. 5 4394
Google Scholar
[20] Frisch M J, Trucks G W, Schlegel H B, Scuseria G E, Robb M A, Cheeseman J R, Scalmani G, Barone V, Mennucci B, Petersson G A, Nakatsuji H, Caricato M, Li X, Hratchian H P, Izmaylov A F, Bloino J, Zheng G, Sonnenberg J L, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery J A Jr, Peralta J E, Ogliaro F, Bearpark M, Heyd J J, Brothers E, Kudin K N, Staroverov V N, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant J C, Iyengar S S, Tomasi J, Cossi M, Rega N, Millam J M, Klene M, Knox J E, Cross J B, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann R E, Yazyev O, Austin A J, Cammi R, Pomelli C, Ochterski J W, Martin R L, Morokuma K, Zakrzewski V G, Voth G A, Salvador P, Dannenberg J J, Dapprich S, Daniels A D, Farkas Ö, Foresman J B, Ortiz J V, Cioslowski J, Fox D J 2009 Gaussian09 (Revision E.01)
[21] Vosko S H, Wilk L, Nusair M 1980 Can. J. Phys. 58 1200
Google Scholar
[22] Krishnan R, Binkley J S, Seeger R, Pople J A 1980 J. Chem. Phys. 72 650
Google Scholar
[23] Møller C, Plesset M S 1934 Phys. Rev. 46 618
Google Scholar
-
[1] 佟赞, 杨银利, 徐晶, 刘伟, 陈亮. 冠醚石墨烷对氦气分离性能的理论研究. , 2023, 72(6): 068201. doi: 10.7498/aps.72.20222183 [2] 崔子纯, 杨莫涵, 阮晓鹏, 范晓丽, 周峰, 刘维民. 高通量计算二维材料界面摩擦. , 2023, 72(2): 026801. doi: 10.7498/aps.72.20221676 [3] 邱子阳, 陈岩, 邱祥冈. 拓扑材料BaMnSb2的红外光谱学研究. , 2022, 71(10): 107201. doi: 10.7498/aps.71.20220011 [4] 李文涛, 袁美玲, 王杰敏. C++H2反应的动力学研究: 基于一个新构建的势能面. , 2022, 71(9): 093402. doi: 10.7498/aps.71.20212241 [5] 施斌, 袁荔, 唐天宇, 陆利敏, 赵先豪, 魏晓楠, 唐延林. 特丁基对苯二酚的光谱及密度泛函研究. , 2021, 70(5): 053102. doi: 10.7498/aps.70.20201555 [6] 赵文丽, 王永刚, 张路路, 岳大光, 孟庆田. 基于新CH2( ${\tilde {\bf{X}}{}^3}{\bf{A''}}$ )势能面的${\bf C}{\bf({}^3}{\bf{P})} + {\bf{H}_2(}{\bf X^1}\Sigma _{\bf g}^ + {\bf )} $ $ \to {\bf H({}^2}{\bf S}) + {\bf CH}{(\bf{}^2}\Pi ) $ 反应量子波包动力学. , 2020, 69(8): 083401. doi: 10.7498/aps.69.20200132[7] 吴晨晨, 郭相东, 胡海, 杨晓霞, 戴庆. 石墨烯等离激元增强红外光谱. , 2019, 68(14): 148103. doi: 10.7498/aps.68.20190903 [8] 许兵, 邱子阳, 杨润, 戴耀民, 邱祥冈. 拓扑半金属的红外光谱研究. , 2019, 68(22): 227804. doi: 10.7498/aps.68.20191510 [9] 王安静, 方勇华, 李大成, 崔方晓, 吴军, 刘家祥, 李扬裕, 赵彦东. 面阵探测下的污染云团红外光谱仿真. , 2017, 66(11): 114203. doi: 10.7498/aps.66.114203 [10] 迟宝倩, 刘轶, 徐京城, 秦绪明, 孙辰, 白晟灏, 刘一璠, 赵新洛, 李小武. 石墨炔衍生物结构稳定性及电子结构的密度泛函理论研究. , 2016, 65(13): 133101. doi: 10.7498/aps.65.133101 [11] 杨雪, 闫冰, 连科研, 丁大军. 1,2-环己二酮基态光解离反应的理论研究. , 2015, 64(21): 213101. doi: 10.7498/aps.64.213101 [12] 韩玉龙, 李真, 汪江洪, 凤尔银, 黄武英. Mg-CO体系的相互作用势和光谱预测. , 2013, 62(9): 093101. doi: 10.7498/aps.62.093101 [13] 李鑫, 羊梦诗, 叶志鹏, 陈亮, 徐灿, 储修祥. 甘氨酸色氨酸寡肽链的红外光谱的密度泛函研究. , 2013, 62(15): 156103. doi: 10.7498/aps.62.156103 [14] 刘晓东, 陶万军, 郑旭光, 萩原雅人, 孟冬冬, 张森林, 郭其新. 磁几何阻挫材料羟基氯化钴的中红外光谱特征. , 2011, 60(3): 037803. doi: 10.7498/aps.60.037803 [15] 逯振平, 韩 奎, 李海鹏, 张文涛, 黄志敏, 沈晓鹏, 张兆慧, 白 磊. 4-N-甲基苯乙烯砒啶盐衍生物振动超极化率的理论研究. , 2007, 56(10): 5843-5848. doi: 10.7498/aps.56.5843 [16] 余春日, 凤尔银, 程新路, 杨向东. He-HI复合物势能面及微分散射截面的理论研究. , 2007, 56(8): 4441-4447. doi: 10.7498/aps.56.4441 [17] 姜振益, 李盛涛. NiTi合金势能面的第一性原理研究. , 2006, 55(11): 6032-6035. doi: 10.7498/aps.55.6032 [18] 韩慧仙, 彭 谦, 文振翼, 王育彬. S2O分子的局域势能面和振动光谱的解析. , 2005, 54(1): 78-84. doi: 10.7498/aps.54.78 [19] 杨武保, 王久丽, 张谷令, 范松华, 刘赤子, 杨思泽. 丙酮环境下ECR微波等离子体辅助化学气相沉积类金刚石薄膜研究. , 2004, 53(9): 3099-3103. doi: 10.7498/aps.53.3099 [20] 王晓艳, 丁世良. 用李代数方法构造四原子分子的势能面. , 2004, 53(2): 423-426. doi: 10.7498/aps.53.423
下载:
计量
- 文章访问数: 6440
- PDF下载量: 163
- 被引次数: 0
