-
突触输入刺激神经元产生的电活动, 在神经编码中发挥着重要作用. 通常认为, 兴奋性输入增强电活动, 抑制性输入压制电活动. 本文选取可调节电流衰减速度的突触模型, 研究了兴奋性自突触在亚临界Hopf分岔附近压制神经元电活动的反常作用, 与抑制性自突触的压制作用进行了比较, 并采用相位响应曲线和相平面分析解释了压制作用的机制. 对于单稳的峰放电, 快速和中速衰减的兴奋性自突触分别可以诱发频率降低的峰放电和混合振荡(峰放电与阈下振荡的交替), 而中速和慢速衰减的抑制性自突触也可以分别诱发频率降低的峰放电和混合振荡. 对于与静息共存的峰放电, 除上述两种行为外, 中速衰减的兴奋性和慢速衰减的抑制性自突触还可以诱发静息. 兴奋性和抑制性自突触电流在不同的衰减速度下, 分别作用在峰放电的不同相位, 才能诱发同类压制行为. 结果丰富了兴奋性突触压制电活动反常作用的实例, 获得了兴奋性和抑制性自突触压制作用机制的不同, 给出了调控神经放电的新手段.Neural activities driven by synaptic inputs are important for neural coding. In general, excitatory synaptic inputs facilitate the firing activities of neurons, and inhibitory synaptic inputs suppress the firing activities. In the present work, the autapse model with adjustable current decay speed is considered, and the suppression effects of excitatory autapse on neuronal firing responses are simulated near subcritical Hopf bifurcation in the Morris-Lecar (ML) neuron model, which are compared with the suppression effects of the inhibitory autapse. Furthermore, the dynamical mechanisms of the suppression effects are acquired with the help of the phase response curve and phase trajectories perturbed by excitatory autaptic current. Near the subcritical Hopf bifurcation, the ML neuron exhibits monostable periodic spiking and coexistence of periodic spiking and resting state. For monostable periodic spiking, excitatory autaptic current with fast and middle decay speeds can induce the periodic spiking with reduced firing frequency and the mixed-mode oscillations (MMOs) that are alternations between subthreshold oscillations and a spike, respectively, and inhibitory autaptic current with middle and slow decay speeds can also induce these two behaviors, respectively. For the periodic spiking in the coexistence region, besides the above two behaviors, excitatory autaptic current with middle decay speed and inhibitory autaptic current with slow decay speed can induce the change from spiking to resting state. The results enrich the paradoxical cases that excitatory inputs suppress the neuronal firing responses, and present the different nonlinear mechanisms in the suppression effects of excitatory and inhibitory self-feedbacks on the neuronal spiking, which provide novel measures to modulate neuronal firing activity.
-
Keywords:
- neural firing /
- autapse /
- subcritical Hopf bifurcation /
- phase response curve
[1] Izhikevich E M 2000 Int. J. Bifurcat. Chaos 10 1171
Google Scholar
[2] Izhikevich E M 2004 IEEE Trans. Neural Networks 15 1063
Google Scholar
[3] Bean B P 2007 Nat. Rev. Neurosci. 8 451
Google Scholar
[4] Bartos M, Vida I, Jonas P 2007 Nat. Rev. Neurosci. 8 45
Google Scholar
[5] Tateno T, Pakdaman K 2004 Chaos 14 511
Google Scholar
[6] Lee S G, Neiman A, Kim S 1998 Phys. Rev. E 57 3292
Google Scholar
[7] Prescott S A, De Koninck Y, Sejnowski T J 2008 PloS Comput. Biol. 4 e1000198
Google Scholar
[8] Ermentrout B 1996 Neural Comput. 8 979
Google Scholar
[9] Smeal R M, Ermentrout G B, White J A 2010 Philos. Trans. R. Soc. London, Ser. B 365 2407
Google Scholar
[10] Goldwyn J H, Slabe B R, Travers J B, Terman D 2018 PloS Comput. Biol. 14 e1006292
Google Scholar
[11] Guo D Q, Wang Q Y, Perc M 2012 Phys. Rev. E 85 061905
Google Scholar
[12] Silver R A 2010 Nat. Rev. Neurosci. 11 474
Google Scholar
[13] Ferrante M, Shay C F, Tsuno Y, Chapman G W, Hasselmo M E 2017 Cereb. Cortex 27 2111
[14] Zhao Z G, Li L, Gu H G, Gao Y 2020 Nonlinear Dyn. 99 1129
Google Scholar
[15] Dodla R, Rinzel J 2006 Phys. Rev. E 73 010903
Google Scholar
[16] Dodla R, Svirskis G, Rinzel J 2006 J. Neurophysiol. 95 2664
Google Scholar
[17] Van Vreeswijk C, Abbott L F, Bard Ermentrout G 1994 J. Comput. Neurosci. 1 313
Google Scholar
[18] Wang X J, Buzsaki G 1996 J. Neurosci. 16 6402
Google Scholar
[19] Vida I, Bartos M, Jonas P 2006 Neuron 49 107
Google Scholar
[20] Li L, Zhao Z G, Gu H G 2019 Int. J. Bifurcat. Chaos 29 1950147
Google Scholar
[21] Uzuntarla M, Torres J J, Calim A, Barreto E 2019 Neural Networks 110 131
Google Scholar
[22] Van Der Loos H, Glaser E M 1972 Brain Res. 48 355
Google Scholar
[23] Bacci A, Huguenard J R 2006 Neuron 49 119
Google Scholar
[24] Cobb S R, Halasy K, Vida I, Nyiri G, Tamas G, Buhl E H, Somogyi P 1997 Neuroscience 79 629
Google Scholar
[25] Yin L P, Zheng R, Ke W, He Q S, Zhang Y, Li J L, Wang B, Mi Z, Long Y S, Rasch M J, Li T F, Luan G M, Shu Y S 2018 Nat. Commun. 9 4890
Google Scholar
[26] Saada R, Miller N, Hurwitz I, Susswein A J 2009 Curr. Biol. 19 479
Google Scholar
[27] Bacci A, Huguenard J R, Prince D A 2003 J. Neurosci. 23 859
Google Scholar
[28] Wang H T, Chen Y 2015 Chin. Phys. B 24 128709
Google Scholar
[29] Yilmaz E, Ozer M, Baysal V, Perc M 2016 Sci. Rep. 6 30914
Google Scholar
[30] Yang X L, Yu Y H, Sun Z K 2017 Chaos 27 083117
Google Scholar
[31] Qin H X, Wu Y, Wang C N, Ma J 2015 Commun. Nonlinear Sci. Numer. Simul. 23 164
Google Scholar
[32] Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China Technol. Sci. 59 364
Google Scholar
[33] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. Astron. 57 1918
Google Scholar
[34] Ma J, Song X L, Tang J, Wang C N 2015 Neurocomputing 167 378
Google Scholar
[35] Yilmaz E, Baysal V, Ozer M, Perc M 2016 Physica A 444 538
Google Scholar
[36] Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 043113
Google Scholar
[37] Li Y Y, Schmid G, Hanggi P, Schimansky-Geier L 2010 Phys. Rev. E 82 061907
Google Scholar
[38] Wang H T, Ma J, Chen Y L, Chen Y 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3242
Google Scholar
[39] Guo D Q, Wu S D, Chen M M, Perc M, Zhang Y S, Ma J L, Cui Y, Xu P, Xia Y, Yao D Z 2016 Sci. Rep. 6 26096
Google Scholar
[40] Guo D Q, Chen M M, Perc M, Wu S D, Xia C, Zhang Y S, Xu P, Xia Y, Yao D Z 2016 Europhys. Lett. 114 30001
Google Scholar
[41] Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760
Google Scholar
[42] Song X L, Wang H T, Chen Y 2019 Nonlinear Dyn. 96 2341
Google Scholar
[43] Zhao Z G, Li L, Gu H G 2020 Sci. Rep. 10 3646
Google Scholar
[44] 曹奔, 关利南, 古华光 2018 67 240502
Google Scholar
Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502
Google Scholar
[45] 丁学利, 李玉叶 2016 65 210502
Google Scholar
Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502
Google Scholar
[46] Li Y Y, Gu H G, Jia Bing, Ding X L 2021 Sci. China Technol. Sci. 64 1459
Google Scholar
[47] Tikidji-Hamburyan R A, Martinez J J, White J A, Canavier C C 2015 J. Neurosci. 35 15682
Google Scholar
[48] 谢勇, 程建慧 2017 66 090501
Google Scholar
Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501
Google Scholar
[49] Wilson C J 2017 J. Neurophysiol. 118 855
Google Scholar
[50] Canavier C C, Wang S G, Chandrasekaran L 2013 Front. Neural Circuits 7 194
[51] 丁学利, 贾冰, 李玉叶 2019 68 180502
Google Scholar
Ding X L, Jia B, Li Y Y 2019 Acta Phys. Sin. 68 180502
Google Scholar
[52] Zhao Z, Li L, Gu H 2020 Commun. Nonlinear Sci. Numer. Simul. 85 105250
Google Scholar
[53] Moss S J, Smart T G 2001 Nat. Rev. Neurosci. 2 240
[54] Prescott S A, Ratte S, De Koninck Y, Sejnowski T J 2008 J. Neurophysiol. 100 3030
Google Scholar
[55] Ermentrout B 2002 Simulating, Analyzing, and Animating Dynamical Systems: A guide to XPPAUT for Researchers and Students (Philadelphia: SIAM) pp77–173
[56] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
Google Scholar
[57] Drion G, O'Leary T, Marder E 2015 Proc. Natl. Acad. Sci. U. S. A. 112 E5361
Google Scholar
[58] Coggan J S, Ocker G K, Sejnowski T J, Prescott S A 2011 J. Neural Eng. 8 065002
Google Scholar
[59] Rho Y A, Prescott S A 2012 PloS Comput. Biol. 8 e1002524
Google Scholar
[60] Dipoppa M, Gutkin B S 2013 Proc. Natl. Acad. Sci. U. S. A. 110 12828
Google Scholar
-
图 1 ML神经元模型(方程(1)和方程(2))动力学行为随
${I_{{\text{app}}}}$ 变化 (a) 分岔, 红色(虚)实线为(不)稳定平衡点, 黑色(空)实心圆为(不)稳定极限环的最小值和最大值; (b) 放电频率Fig. 1. Changes of dynamical behavior of the ML neuron model (Equation (1) and (2)) with respect to
${I_{{\text{app}}}}$ : (a) Bifurcations, red (dashed) solid curve denotes (unstable) stable equilibria, and black solid (empty) circles denote minima and maxima of (unstable) stable limit cycles; (b) firing frequency.
图 3 当
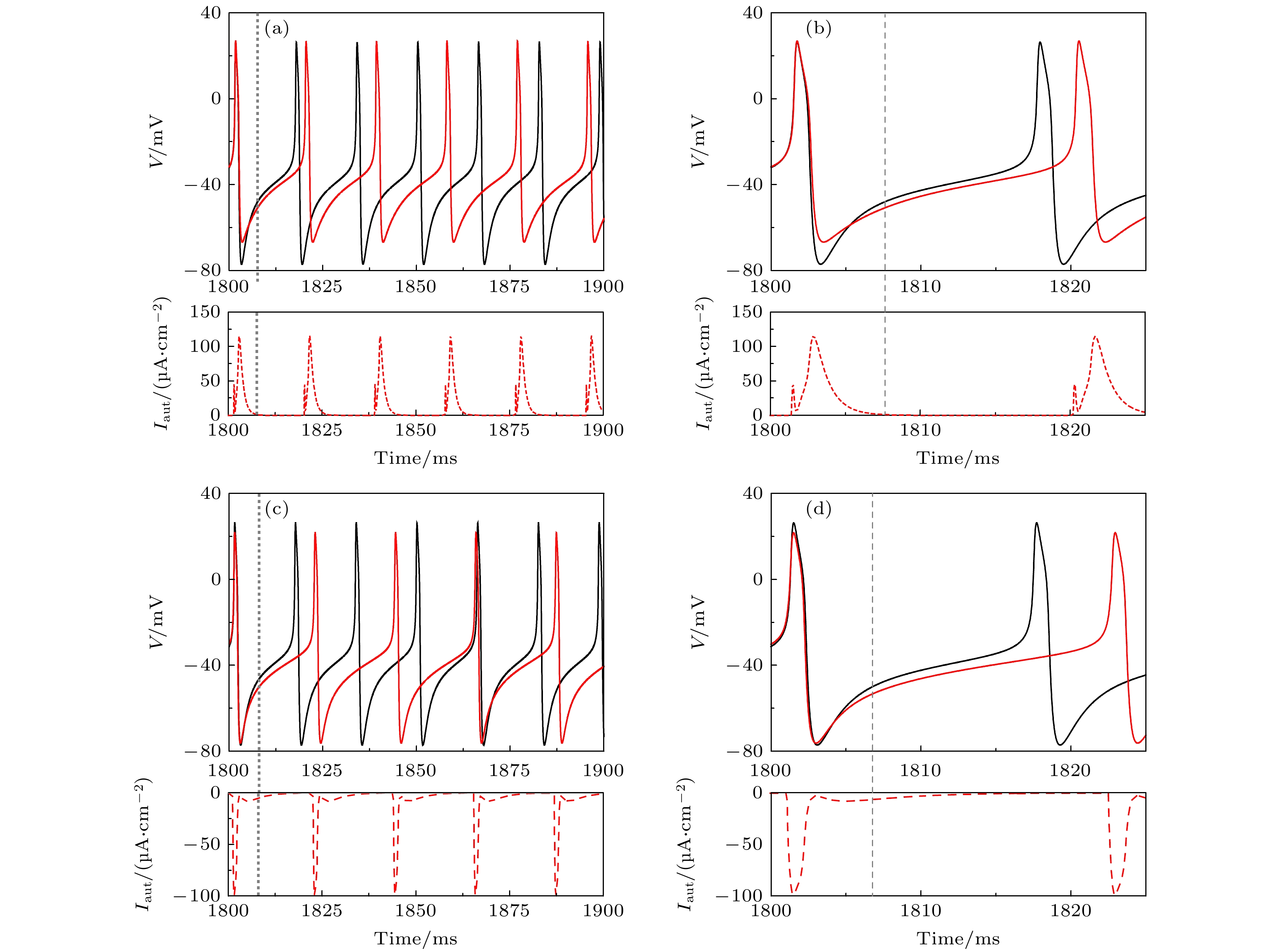
${I_{{\text{app}}}} = 42.{\text{6}}\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ 时, 不同自突触诱导的频率降低的周期峰放电 (a)${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 1.0\;{\text{m}}{{\text{s}}^{ - 1}}$ 的兴奋性自突触; (b) 图(a)的局部放大图; (c)${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.3\;{\text{m}}{{\text{s}}^{ - 1}}$ 的抑制性自突触; (d) 图(c)的局部放大图. 黑和红色实线分别为ML神经元模型(方程(1)和方程(2))和自突触耦合ML神经元模型(方程(3)—(5))的膜电位, 红色虚线为自突触电流, 灰色虚线为黑色实线第一个峰峰间隙PRC的相位滞后和提前的临界点, 图(a)和图(b)中灰色虚线的左右两侧分为兴奋性刺激PRC的相位滞后和提前区域, 图(c)和图(d)中灰色虚线的左右两侧分为抑制性刺激PRC的相位提前和滞后区域Fig. 3. Periodic spiking with reduced firing frequency induced by different autapses when
${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ : (a) Excitatory autapse with${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 1.0\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (b) enlargement of Figure (a); (c) inhibitory autapse with${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.3\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (d) enlargement of Figure (c). Black and red solid curves are the membrane potential for the ML neuron model (Equation (1) and (2)) and the ML neuron model with autapse (Equation (3)–(5)), respectively. Red dashed curve is the autaptic current, gray dashed vertical lines is critical border between phase delay and phase advance regions of the PRC for the first interspike interval of the black solid curve, the left and right sides of the gray dashed line in Figure (a) and Figure (b) respectively are the phase delay and advance regions of the PRC, the left and right sides of the gray dashed line in Figure (c) and Figure (d) respectively are phase advance and delay regions of the PRC.
图 4 当
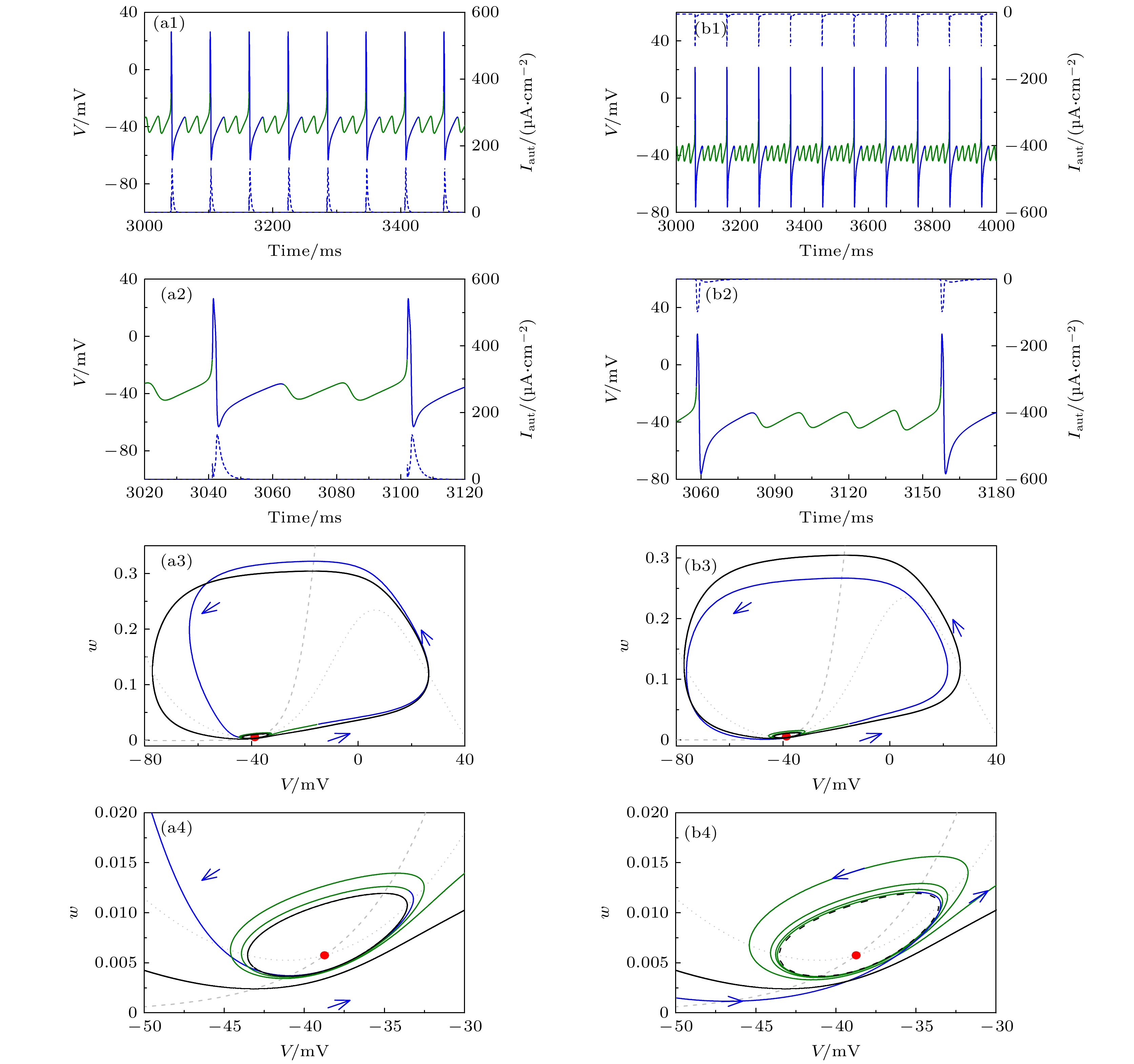
${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ 时, 不同自突触诱发共存峰放电(黑色实线)变为静息(红色实线) (a1)${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = $ $ 0.4\;{\text{m}}{{\text{s}}^{ - 1}}$ 的兴奋性自突触; (a2) 图(a1)的局部放大; (a3) 图(a1)的相平面图; (a4) 图(a3)的局部放大; (b1)${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.1\;{\text{m}}{{\text{s}}^{ - 1}}$ 的抑制性自突触; (b2) 图(b1)的局部放大; (b3) 对应于(b1)的相平面图; (b4) 图(b3)的局部放大. 在图(a1)和图(b1)中, 黑色实线为ML神经元模型(方程(1)和方程(2))膜电位, 蓝色和红色实线为自突触耦合ML神经元模型(方程(3)—(5))膜电位, 蓝色虚线为突触电流, 蓝色实线是对应于突触电流的膜电位. 在图(a3)和图(b3)中, 蓝色和红色实线分别对应于图(a1)和图(b1)中蓝色和红色实线的相轨迹. 灰色虚线和点线分别为方程(1)和方程(2)的$w$ 和$V$ 零等倾斜线, 黑色实线和虚线分别为方程(1)和方程(2)的稳定和不稳定极限环, 红色实心点为方程(1)和方程(2)的稳定平衡点, 蓝色箭头表示相轨迹的方向, 青色实心点为兴奋性和抑制性突触电流改变相轨迹方向的关键相位Fig. 4. Resting state (solid red curve) evoked from coexisting spiking (solid black curve) by different autapses when
${I_{{\text{app}}}} = $ $ 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ : (a1) Excitatory autapse with${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.4\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (a2) enlargement of Figure (a1); (a3) phase portrait corresponds to Figure (a1); (a4) enlargement of Figure (a3); (b1) inhibitory autapse with${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = $ $ 0.1\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (b2) enlargement of Figure (b1); (b3) phase portrait corresponds to Figure (b1); (b4) enlargement of Figure (b3). In Figure (a1) and Figure (b1), black solid line is the membrane potential of the ML neuron (Equation (1) and (2)), blue and red solid lines are membrane potential of the ML neuron with autapse (Equation (3)-(5)), blue dashed curve is the autaptic current and the blue solid curve is membrane potential effected by the autaptic current. In Figure (a3) and Figure (b3), blue and red solid curves are the trajectories corresponding to the blue and red solid parts in Figure (a1) and Figure (b1), respectively, gray dashed (dotted) curve is the nullcline$\dot w = 0$ ($\dot V = 0$ ) of Equation (1) and (2), black solid (dashed) curve is the stable (unstable) limit cycle of Equation (1) and (2), red solid circle is the stable focus of Equation (1) and (2), blue arrow denotes the direction of the trajectory, cyan solid circle is a critical point that determines the direction of trajectory affected by the excitatory or inhibitory autaptic current.
图 5 当
${I_{{\text{app}}}} = 42.{\text{6}}\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ 时, 不同自突触诱发共存峰放电变为混合振荡(蓝、绿实线) (a1)${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.{\text{56}}\;{\text{m}}{{\text{s}}^{ - 1}}$ 的兴奋性自突触; (a2) 图(a1)的局部放大; (a3) 对应于图(a1)的相平面; (a4) 图(a3)的局部放大; (b1)${g_{{\text{inh}}}} = {\text{1}}{\text{.0}}\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = $ $ 0.{\text{263}}\;{\text{m}}{{\text{s}}^{ - 1}}$ 的抑制性自突触; (b2) 图(b1)的局部放大; (b3) 对应于(b1)的相平面; (b4) 图(b3)的局部放大. 在图(a1)和(b1)中, 黑色实线为ML神经元模型(方程(1)和方程(2))膜电位, 蓝色和绿色实线为自突触耦合ML神经元模型(方程(3)—(5))膜电位, 蓝色虚线为突触电流, 蓝色实线是对应于突触电流的部分. 在图(a3)和图(b3)中, 蓝色和绿色实线分别对应于图(a1)和图(b1)中蓝色和绿色实线的相轨迹. 灰色虚线和点线分别为方程(1)和方程(2)的$w$ 和$V$ 零等倾斜线, 黑色实线和虚线分别为方程(1)和方程(2)的稳定和不稳定极限环, 红色实心点为方程(1)和方程(2)的稳定平衡点, 蓝色箭头表示相轨迹的方向Fig. 5. Mixed-mode oscillations (blue and green solid curves) evoked from coexisting spiking by different autapses when
${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ : (a1) Excitatory autapse with${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.{\text{56}}\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (a2) enlargement of Figure (a1); (a3) phase portrait corresponds to Figure (a1); (a4) enlargement of (a3); (b1) inhibitory autapse with${g_{{\text{inh}}}} = {\text{1}}{\text{.0}}\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.{\text{263}}\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (b2) enlargement of Figure (b1); (b3) phase portrait corresponds to Figure (b1); (b4) enlargement of Figure (b3). In Figure (a1) and Figure (b1), black solid line is the membrane potential of the ML neuron (Equation (1) and (2)), blue and green solid lines are membrane potential of the ML neuron with autapse (Equation (3)—(5)), blue dashed curve is the autaptic current and the blue solid curve is membrane potential effected by autaptic current. In Figure(a3) and Figure (b3), blue and green solid curves respectively are the trajectories corresponding to the blue and green solid parts in Figure (a1) and Figure (b1), gray dashed (dotted) curve is the nullcline$\dot w = 0$ ($\dot V = 0$ ) of Equation (1) and (2), black solid (dashed) curve is the stable (unstable) limit cycle of Equation (1) and (2), red solid circle is the stable focus of Equation (1) and (2), blue arrow denotes the direction of the trajectory.
图 6 当
${I_{{\text{app}}}} = 42.9\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ 时, 不同自突触引起的单稳峰放电到混合振荡(蓝和绿实线)的转变 (a1)${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.35\;{\text{m}}{{\text{s}}^{ - 1}}$ 的兴奋性自突触; (a2) 图(a1)的局部放大; (a3) 对应于(a1)的相平面图; (a4) 图(a3)的局部放大; (b1)${g_{{\text{inh}}}} = $ $ 1.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.1\;{\text{m}}{{\text{s}}^{ - 1}}$ 的抑制性自突触; (b2) 图(b1)的局部放大; (b3) 对应于(b1)的相平面图; (b4) 图(b3)的局部放大. 在图(a1)和图(b1)中, 蓝色和绿色实线为自突触耦合ML神经元模型(方程(3)—(5))膜电位, 蓝色虚线为突触电流, 蓝色实线是对应于突触电流的部分. 在图(a3)和图(b3)中, 蓝色和绿色实线分别对应于图(a1)和图(b1)中蓝色和绿色实线的相轨迹. 灰色虚线和点线分别为方程(1)和方程(2)的$w$ 和$V$ 零等倾斜线, 黑色实线和虚线分别为方程(1)和方程(2)的稳定和不稳定极限环, 红色空心点为方程(1)和方程(2)的稳定平衡点, 蓝色箭头表示相轨迹的方向Fig. 6. The mixed-mode oscillations (blue and red curves) evoked from the monostable spiking by different autapses when
${I_{{\text{app}}}} = 42.9\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ : (a1) Excitatory autapse with${g_{{\text{exc}}}} = 2.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.35\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (a2) enlargement of Figure (a1); (a3) phase portrait corresponding to Figure (a1); (a4) enlargement of Figure (a3); (b1) inhibitory autapse with${g_{{\text{inh}}}} = {\text{1}}{\text{.0}}\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.1\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (b2) enlargement of Figure (b1); (b3) phase portrait corresponds to Figure (b1); (b4) enlargement of Figure (b3). In Figure (a1) and Figure (b1), blue and green solid lines are membrane potential of the ML neuron with autapse (Equation (3)—(5)), blue dashed curve is the autaptic current and the blue solid curve is membrane potential effected by the autaptic current. In Figure (a3) and Figure (b3), blue and green solid curves respectively are the trajectories corresponding to the blue and green solid parts in Figure (a1) and Figure (b1), gray dashed (dotted) curve is the nullcline$\dot w = 0$ ($\dot V = 0$ ) of Equation (1) and (2), black solid curve is the stable limit cycle of Equation (1) and (2), red hollow circle is the stable focus of Equation (1) and (2), blue arrow denotes the direction of the trajectory.
图 7 不同
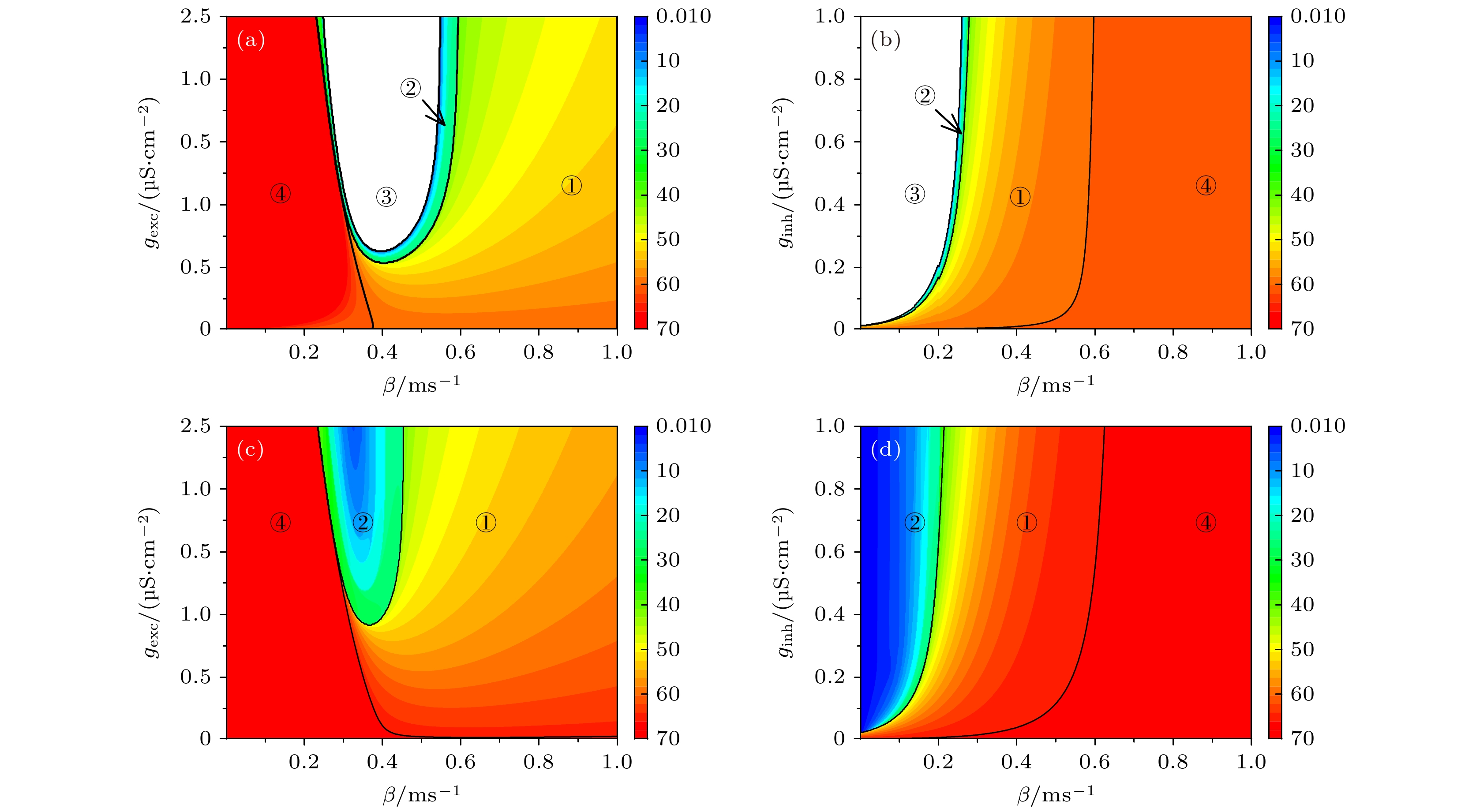
${I_{{\text{app}}}}$ 下, 不同自突触诱发的不同动力学行为及其频率在参数平面$\beta $ 和${g_{{\text{exc}}}}$ (${g_{{\text{inh}}}}$ )上的分布.${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ (共存峰放电) (a) 兴奋性自突触; (b) 抑制性自突触.${I_{{\text{app}}}} = 43\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ (单稳峰放电) (c) 兴奋性自突触; (d) 抑制性自突触. 黑线为不同电活动的分界线, 区域①, ②和③分别为频率降低的周期峰放电、混合振荡和静息, 区域④为频率增加的周期峰放电. 色标代表放电频率Fig. 7. Distribution of different dynamical behaviors and firing frequency induced by different autapses on the parameter plane
$({g_{{\text{exc}}}}, \beta )$ or$({g_{{\text{inh}}}}, \beta )$ when${I_{{\text{app}}}}$ is fixed at different values,${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ (coexisting spiking): (a) Excitatory autapse; (b) inhibitory autapse.${I_{{\text{app}}}} = 43\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ (monostable spiking): (c) Excitatory autapse; (d) inhibitory autapse. Black curve is the border of different firing activities. Regions ①, ② and ③ are periodic spiking with reduced firing frequency, mixed-mode oscillations, and resting state, respectively, region ④ is periodic spiking with enhanced firing frequency. The color scale represents firing frequency.
图 8 当
${I_{{\text{app}}}} = 42.{\text{6}}\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ 时, 不同自突触诱导出的频率增加的周期峰放电 (a)${g_{{\text{exc}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 0.26\;{\text{m}}{{\text{s}}^{ - 1}}$ 的兴奋性自突触; (b) 图(a)的局部放大; (c)${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ 和$\beta = 1.0\;{\text{m}}{{\text{s}}^{ - 1}}$ 的抑制性自突触; (d) 图(c)的局部放大. 黑色实线为无自突触耦合神经元模型(方程(1)和方程(2))的膜电位, 红色实线为自突触耦合神经元模型(方程(3)—(5))的膜电位, 红色虚线为相对应的突触电流, 灰色虚线为黑色实线第一个峰峰间隙PRC的相位滞后和提前的临界点, 图(a)和图(b)中灰色虚线的左右两侧分为兴奋性刺激PRC的相位滞后和提前区域, 图(c)和图(d)中灰色虚线的左右两侧分为抑制性刺激PRC的相位提前和滞后区域Fig. 8. Periodic spiking with increased firing frequency induced by different autapses when
${I_{{\text{app}}}} = 42.6\;{\text{μA/c}}{{\text{m}}^{\text{2}}}$ : (a) Excitatory autapse with${g_{{\text{exc}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 0.26\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (b) enlargement of (a); (c) inhibitory autapse with${g_{{\text{inh}}}} = 1.0\;{\text{μS/c}}{{\text{m}}^2}$ and$\beta = 1.0\;{\text{m}}{{\text{s}}^{ - 1}}$ ; (d) enlargement of Figure (c). Black and red solid curves are the membrane potential for the ML neuron (Equation (1) and (2)) and the ML neuron with autapse (Equation (3)-(5)), respectively, red dashed curve is the autaptic current, gray dashed vertical lines is critical border between phase delay and phase advance regions of the PRC for the first interspike interval (the black solid line), the left and right sides of the gray dashed line in Figure (a) and Figure (b) respectively are phase delay and advance regions of the PRC, the left and right sides of the gray dashed line in Figure (c) and Figure (d) respectively are phase advance and delay regions of the PRC. -
[1] Izhikevich E M 2000 Int. J. Bifurcat. Chaos 10 1171
Google Scholar
[2] Izhikevich E M 2004 IEEE Trans. Neural Networks 15 1063
Google Scholar
[3] Bean B P 2007 Nat. Rev. Neurosci. 8 451
Google Scholar
[4] Bartos M, Vida I, Jonas P 2007 Nat. Rev. Neurosci. 8 45
Google Scholar
[5] Tateno T, Pakdaman K 2004 Chaos 14 511
Google Scholar
[6] Lee S G, Neiman A, Kim S 1998 Phys. Rev. E 57 3292
Google Scholar
[7] Prescott S A, De Koninck Y, Sejnowski T J 2008 PloS Comput. Biol. 4 e1000198
Google Scholar
[8] Ermentrout B 1996 Neural Comput. 8 979
Google Scholar
[9] Smeal R M, Ermentrout G B, White J A 2010 Philos. Trans. R. Soc. London, Ser. B 365 2407
Google Scholar
[10] Goldwyn J H, Slabe B R, Travers J B, Terman D 2018 PloS Comput. Biol. 14 e1006292
Google Scholar
[11] Guo D Q, Wang Q Y, Perc M 2012 Phys. Rev. E 85 061905
Google Scholar
[12] Silver R A 2010 Nat. Rev. Neurosci. 11 474
Google Scholar
[13] Ferrante M, Shay C F, Tsuno Y, Chapman G W, Hasselmo M E 2017 Cereb. Cortex 27 2111
[14] Zhao Z G, Li L, Gu H G, Gao Y 2020 Nonlinear Dyn. 99 1129
Google Scholar
[15] Dodla R, Rinzel J 2006 Phys. Rev. E 73 010903
Google Scholar
[16] Dodla R, Svirskis G, Rinzel J 2006 J. Neurophysiol. 95 2664
Google Scholar
[17] Van Vreeswijk C, Abbott L F, Bard Ermentrout G 1994 J. Comput. Neurosci. 1 313
Google Scholar
[18] Wang X J, Buzsaki G 1996 J. Neurosci. 16 6402
Google Scholar
[19] Vida I, Bartos M, Jonas P 2006 Neuron 49 107
Google Scholar
[20] Li L, Zhao Z G, Gu H G 2019 Int. J. Bifurcat. Chaos 29 1950147
Google Scholar
[21] Uzuntarla M, Torres J J, Calim A, Barreto E 2019 Neural Networks 110 131
Google Scholar
[22] Van Der Loos H, Glaser E M 1972 Brain Res. 48 355
Google Scholar
[23] Bacci A, Huguenard J R 2006 Neuron 49 119
Google Scholar
[24] Cobb S R, Halasy K, Vida I, Nyiri G, Tamas G, Buhl E H, Somogyi P 1997 Neuroscience 79 629
Google Scholar
[25] Yin L P, Zheng R, Ke W, He Q S, Zhang Y, Li J L, Wang B, Mi Z, Long Y S, Rasch M J, Li T F, Luan G M, Shu Y S 2018 Nat. Commun. 9 4890
Google Scholar
[26] Saada R, Miller N, Hurwitz I, Susswein A J 2009 Curr. Biol. 19 479
Google Scholar
[27] Bacci A, Huguenard J R, Prince D A 2003 J. Neurosci. 23 859
Google Scholar
[28] Wang H T, Chen Y 2015 Chin. Phys. B 24 128709
Google Scholar
[29] Yilmaz E, Ozer M, Baysal V, Perc M 2016 Sci. Rep. 6 30914
Google Scholar
[30] Yang X L, Yu Y H, Sun Z K 2017 Chaos 27 083117
Google Scholar
[31] Qin H X, Wu Y, Wang C N, Ma J 2015 Commun. Nonlinear Sci. Numer. Simul. 23 164
Google Scholar
[32] Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China Technol. Sci. 59 364
Google Scholar
[33] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. Astron. 57 1918
Google Scholar
[34] Ma J, Song X L, Tang J, Wang C N 2015 Neurocomputing 167 378
Google Scholar
[35] Yilmaz E, Baysal V, Ozer M, Perc M 2016 Physica A 444 538
Google Scholar
[36] Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 043113
Google Scholar
[37] Li Y Y, Schmid G, Hanggi P, Schimansky-Geier L 2010 Phys. Rev. E 82 061907
Google Scholar
[38] Wang H T, Ma J, Chen Y L, Chen Y 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3242
Google Scholar
[39] Guo D Q, Wu S D, Chen M M, Perc M, Zhang Y S, Ma J L, Cui Y, Xu P, Xia Y, Yao D Z 2016 Sci. Rep. 6 26096
Google Scholar
[40] Guo D Q, Chen M M, Perc M, Wu S D, Xia C, Zhang Y S, Xu P, Xia Y, Yao D Z 2016 Europhys. Lett. 114 30001
Google Scholar
[41] Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760
Google Scholar
[42] Song X L, Wang H T, Chen Y 2019 Nonlinear Dyn. 96 2341
Google Scholar
[43] Zhao Z G, Li L, Gu H G 2020 Sci. Rep. 10 3646
Google Scholar
[44] 曹奔, 关利南, 古华光 2018 67 240502
Google Scholar
Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502
Google Scholar
[45] 丁学利, 李玉叶 2016 65 210502
Google Scholar
Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502
Google Scholar
[46] Li Y Y, Gu H G, Jia Bing, Ding X L 2021 Sci. China Technol. Sci. 64 1459
Google Scholar
[47] Tikidji-Hamburyan R A, Martinez J J, White J A, Canavier C C 2015 J. Neurosci. 35 15682
Google Scholar
[48] 谢勇, 程建慧 2017 66 090501
Google Scholar
Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501
Google Scholar
[49] Wilson C J 2017 J. Neurophysiol. 118 855
Google Scholar
[50] Canavier C C, Wang S G, Chandrasekaran L 2013 Front. Neural Circuits 7 194
[51] 丁学利, 贾冰, 李玉叶 2019 68 180502
Google Scholar
Ding X L, Jia B, Li Y Y 2019 Acta Phys. Sin. 68 180502
Google Scholar
[52] Zhao Z, Li L, Gu H 2020 Commun. Nonlinear Sci. Numer. Simul. 85 105250
Google Scholar
[53] Moss S J, Smart T G 2001 Nat. Rev. Neurosci. 2 240
[54] Prescott S A, Ratte S, De Koninck Y, Sejnowski T J 2008 J. Neurophysiol. 100 3030
Google Scholar
[55] Ermentrout B 2002 Simulating, Analyzing, and Animating Dynamical Systems: A guide to XPPAUT for Researchers and Students (Philadelphia: SIAM) pp77–173
[56] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
Google Scholar
[57] Drion G, O'Leary T, Marder E 2015 Proc. Natl. Acad. Sci. U. S. A. 112 E5361
Google Scholar
[58] Coggan J S, Ocker G K, Sejnowski T J, Prescott S A 2011 J. Neural Eng. 8 065002
Google Scholar
[59] Rho Y A, Prescott S A 2012 PloS Comput. Biol. 8 e1002524
Google Scholar
[60] Dipoppa M, Gutkin B S 2013 Proc. Natl. Acad. Sci. U. S. A. 110 12828
Google Scholar
下载:
计量
- 文章访问数: 4466
- PDF下载量: 83
- 被引次数: 0
