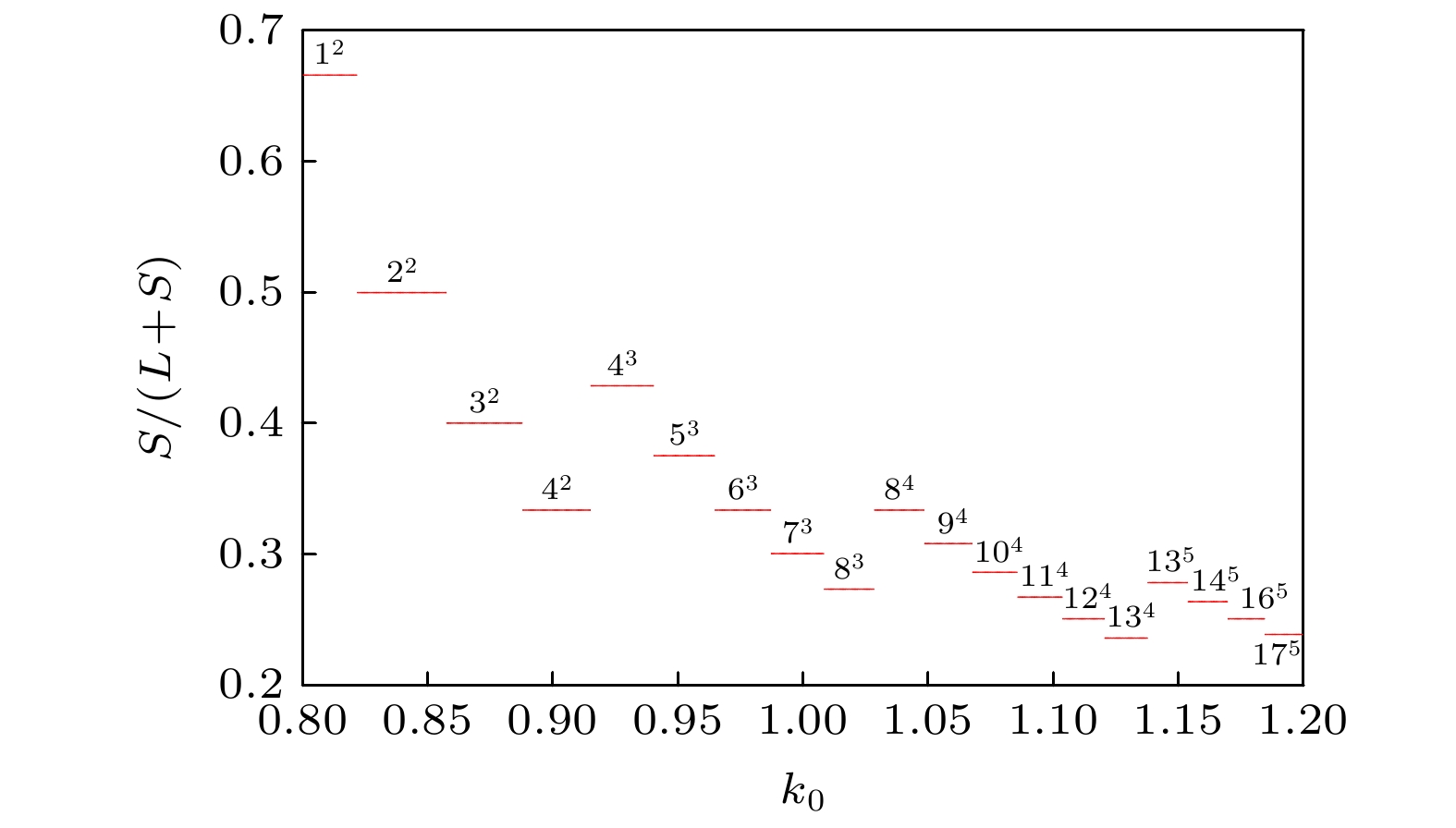
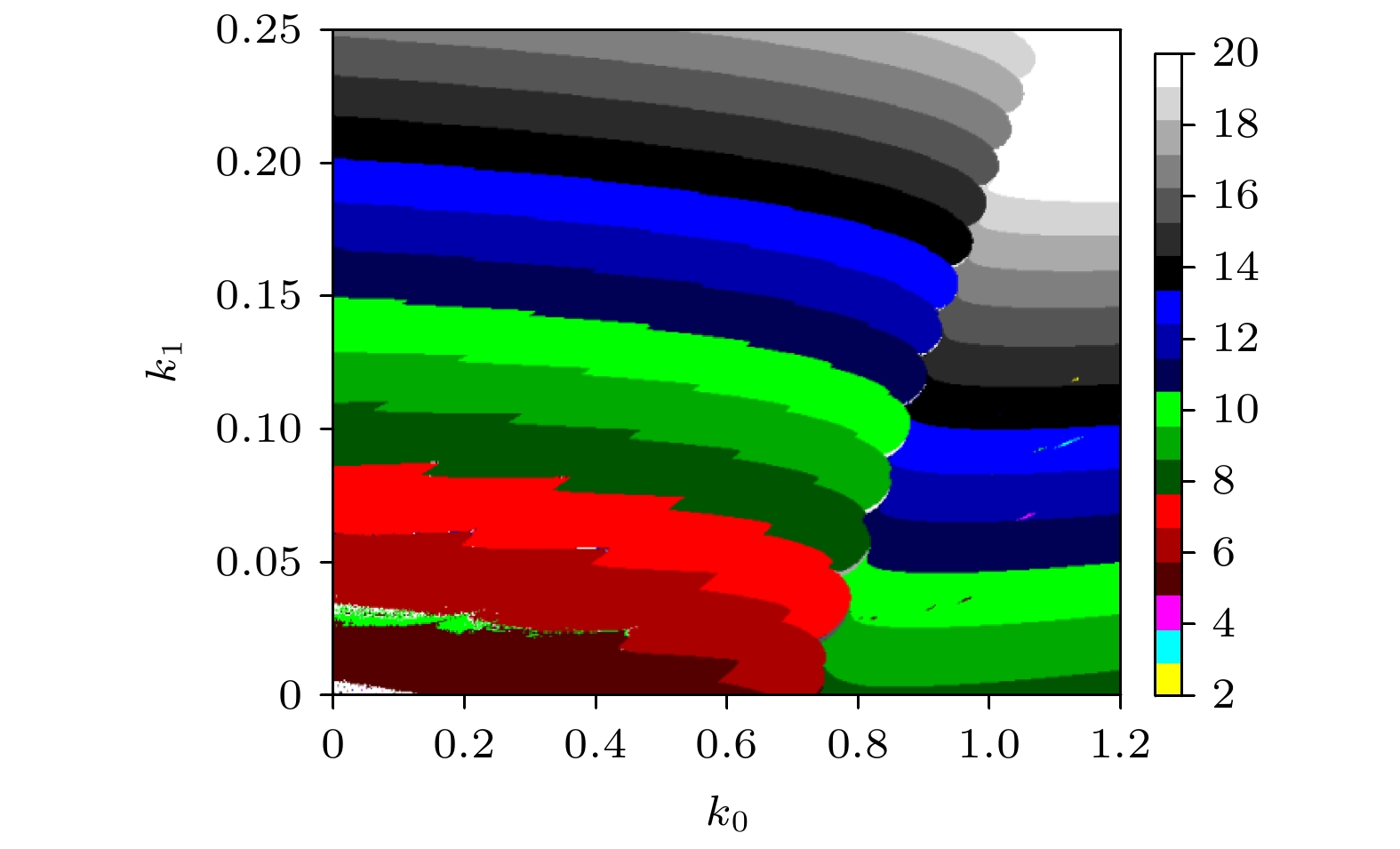
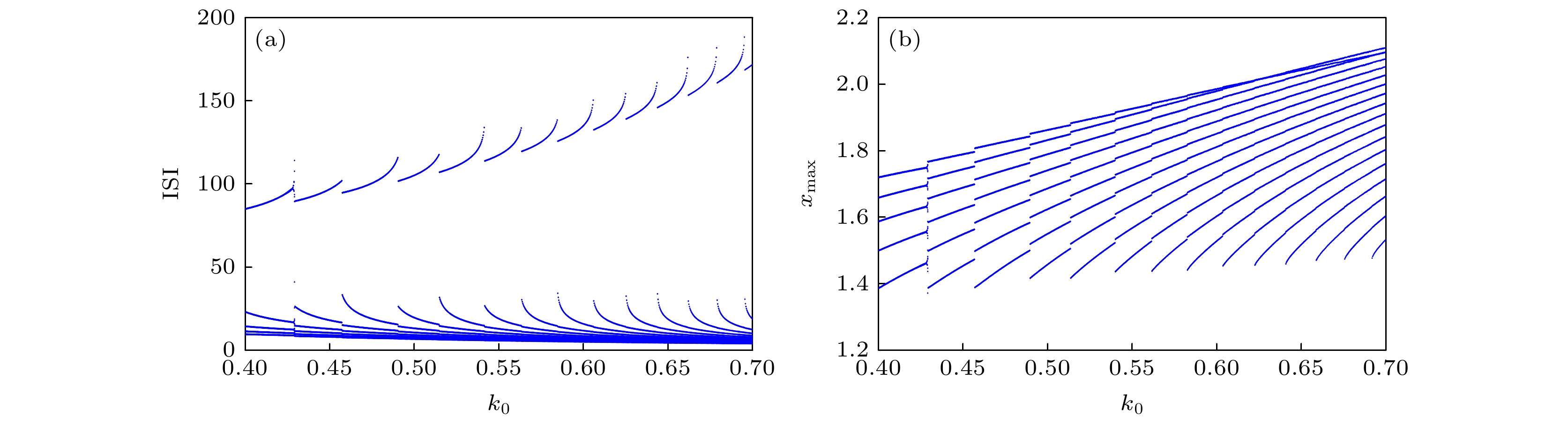
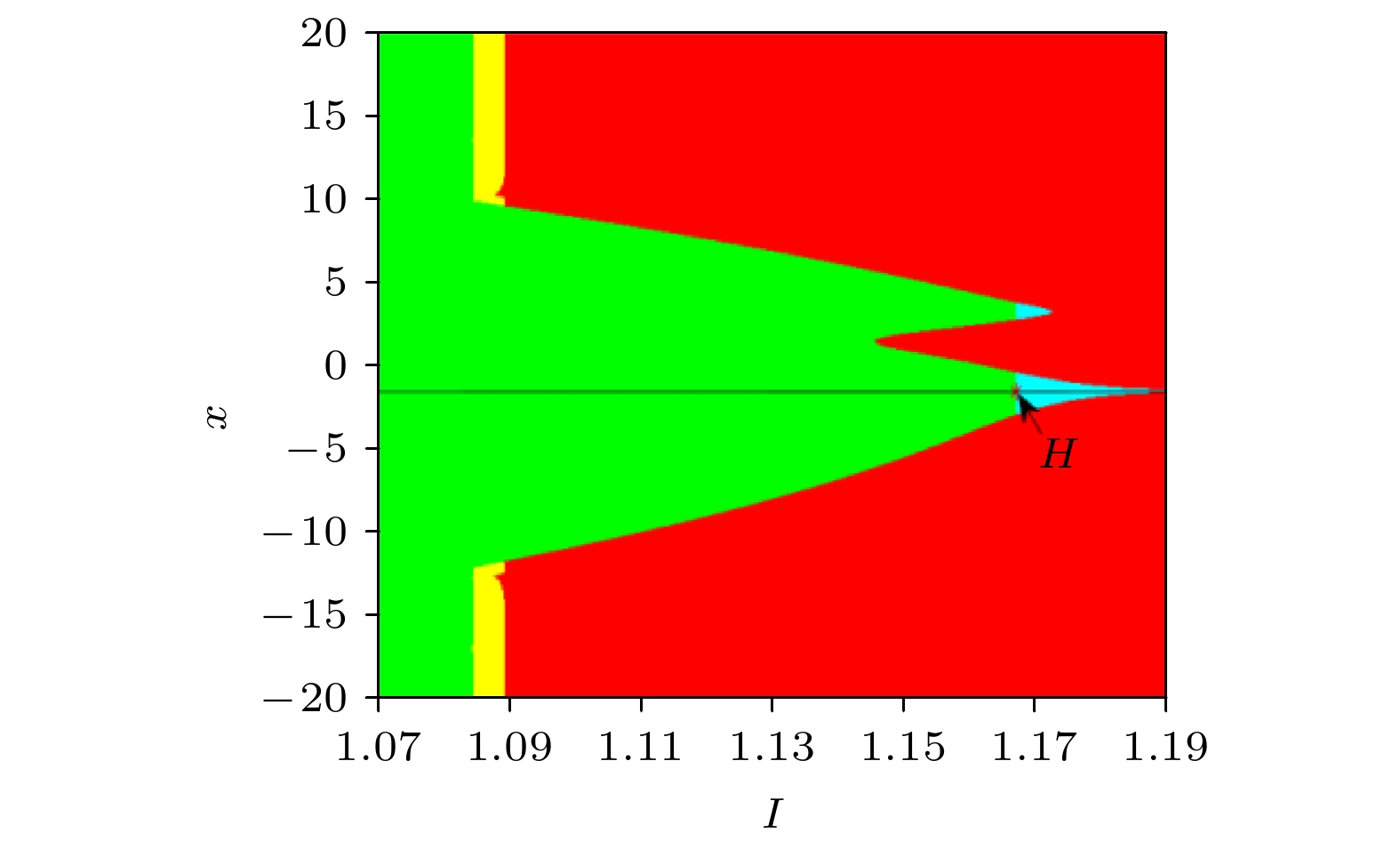
-
钙、钾、钠等离子在细胞内连续泵送和传输时产生的时变电场不仅会影响神经元的放电活动, 而且会诱导时变磁场去进一步调节细胞内离子的传播. 根据麦克斯韦电磁场理论, 时变的电场和磁场在细胞内外的电生理环境中会相互激发而产生电磁场. 为了探究电磁场影响下的神经元放电节律转迁, 本文在三维Hindmarsh-Rose (HR)神经元模型的基础上, 引入磁通变量和电场变量, 建立了一个五维HR神经元模型(简称EMFN模型). 首先, 结合Matcont软件分析了EMFN模型的平衡点分布与全局分岔性质, 发现并分析了该模型存在的亚临界Hopf分岔、隐藏放电及其周期放电与静息态共存等现象. 其次, 利用双参数及单参数分岔、ISI 分岔和最大Lyapunov指数等工具进行数值仿真, 详细分析了EMFN模型存在的伴有混沌及无混沌的加周期分岔结构、混合模式放电和共存模式放电等现象, 同时揭示了电场和磁场强度影响其放电节律的转迁规律. 最后, 利用Washout控制器将EMFN模型的亚临界Hopf分岔转化为超临界Hopf分岔, 使其在分岔点附近的拓扑结构发生改变, 由此达到消除其隐藏放电的目的. 本文的研究结果证实了新建神经元模型具有丰富的放电节律, 将影响神经元的信息传递和编码, 为完善神经元模型, 揭示电磁场对生物神经系统的影响, 以及探求一些神经性疾病的致病机理提供了思路.The time-varying electric fields generated by continuously pumping and transmitting calcium, potassium and sodium ions in cells not only affect the discharge activity of neurons, but also induce time-varying magnetic fields to further regulate the fluctuation of ions. According to the Maxwell's electromagnetic field theory, time-varying electric field and magnetic field can stimulate each other in the electrophysiological environment inside and outside the cells to produce electromagnetic field. In order to explore the discharge rhythm transition of neurons under the influence of electromagnetic fields, a five-dimensional (5D) HR neuron model (EMFN model for short) is established by introducing magnetic flux variable and electric field variable into a three-dimensional (3D) Hindmarsh-Rose (HR) neuron model. Firstly, the equilibrium distribution and global bifurcation properties of EMFN model are analyzed by Matcont software, then the existence of subcritical Hopf bifurcation, hidden discharge, coexistence of periodic discharge and resting state are found and analyzed. Secondly, by using the tools of two-parameter and one-parameter bifurcation, ISI bifurcation and the maximum Lyapunov exponent for numerical simulation, the period-adding bifurcation with and without chaos, mixed mode discharge and coexistence mode discharge in the EMFN model are analyzed in detail. At the same time, the transition law of discharge rhythm with the influence of electric field and magnetic field intensity is revealed. Finally, the Washout controller is used to convert the subcritical Hopf bifurcation into supercritical Hopf bifurcation, so the topological structure of EMFN model near the bifurcation point is changed for eliminating the hidden discharge. The research results of this paper confirm that the novel neuron model has rich discharge rhythm, which will affect the information transmission and coding, and provide some ideas for improving the neuron models, revealing the influence of electromagnetic field on biological nervous system, and exploring the pathogenic mechanism of some neurological diseases.
-
Keywords:
- electromagnetic fields /
- Hopf bifurcation analysis /
- hidden attractor /
- two-parameter bifurcation /
- mixed mode discharge
[1] Varona P, Levi R, Arshavsky Y I, Rabinovich M I, Selverston A I 2004 Neurocomputing 58 549
Google Scholar
[2] Kato R, Yamanaka M, Kobayashi M 2018 J. Pharmacol. Sci. 136 172
Google Scholar
[3] Kayasandik C, Guo K H, Labate D 2019 J. Comput. Appl. Math. 349 482
Google Scholar
[4] 丁学利, 贾冰, 李玉叶 2019 68 180502
Google Scholar
Ding X L, Jia B, Li Y Y 2019 Acta Phys. Sin. 68 180502
Google Scholar
[5] Nielsen B F 2017 J. Math. Neurosci. 7 6
Google Scholar
[6] Shim Y, Husbands P 2018 Adapt. Behav. 26 165
Google Scholar
[7] Otsuka S, Omori T 2019 Neural Netw. 109 137
Google Scholar
[8] 杨永霞, 李玉叶, 古华光 2020 69 040501
Google Scholar
Yang Y X, Li Y Y, Gu H G 2020 Acta Phys. Sin. 69 040501
Google Scholar
[9] Hodgkin A L, Huxley A F 1952 J. Physiol. 116 473
Google Scholar
[10] Morris C, Lecar H 1981 Biophys. J. 35 193
Google Scholar
[11] Chay R T 1983 J. Phys. Chem. 87 2935
Google Scholar
[12] Hindmarsh J L, Rose R M 1984 P. Roy. Soc. B-Biol. Sci. 221 87
Google Scholar
[13] Izhikevich E M 2003 IEEE T. Neural Networ. 14 1569
Google Scholar
[14] FitzHugh R 1961 Biophys. J. 1 445
Google Scholar
[15] Cassidy A S, Merolla P, Arthur J V, Esser S K, Jackson B, Alvarez-Icaza R, Datta P, Sawada J, Wong T M, Feldman V, Amir A, Rubin D B, Akopyan F, McQuinn E, Risk W P, Modha D S 2013 The 2013 International Joint Conference on Neural Networks Dallas, USA, August 4–9, 2013 p1
[16] 徐泠风, 李传东, 陈玲 2016 65 240701
Google Scholar
Xu L F, Li C D, Chen L 2016 Acta Phys. Sin. 65 240701
Google Scholar
[17] Barrio R, Lefranc M, Martínez M A, Serrano S 2015 Europhyslett. Lett. 109 20002
Google Scholar
[18] Yang S M, Wang J, Li S, Li H Y, Wei X L, Yu H T, Deng B 2015 Neurocomputing 177 274
Google Scholar
[19] Babacan Y, Kaçar F, Gürkan K 2016 Neurocomputing 203 86
Google Scholar
[20] Bao B C, Huang A H, Bao H 2018 Complexity 2018 1
Google Scholar
[21] Usha K, Subha P A 2019 Biosystems 5 1
Google Scholar
[22] Zhao Y, Sun X Y, Liu Yang, Kurths J 2018 Nonlinear Dyn. 93 1315
Google Scholar
[23] Pham V T, Jafari S, Vaidyanathan S, Vilos C, Wang X 2016 Sci. China Technol. Sci. 59 358
Google Scholar
[24] Ma J, Tang J 2015 Sci. China Technol. Sci. 58 2038
Google Scholar
[25] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
Google Scholar
[26] Wu F Q, Wang C N, Jin W Y Ma J 2017 Physica A 469 81
Google Scholar
[27] Kafraja M S, Parastesha F, Jafariba S 2020 Chaos, Soliton. Fract. 137 109782
Google Scholar
[28] 安新磊, 张莉 2020 力学学报 52 1174
Google Scholar
An X L, Zhang L 2020 Chin. J. Theor. Appl. Mech. 52 1174
Google Scholar
[29] Ma J, Zhang G, Hayat T, Ren G D 2019 Nonlinear Dyn. 95 1585
Google Scholar
[30] Du L, Cao Z L, Lei Y M, Deng Z C 2019 Sci. China Technol. Sci. 62 1141
Google Scholar
[31] Wang C N, Tang J, Ma J 2019 Eur. Phys. J-Spec. Top. 228 1907
Google Scholar
[32] Oliveira L B, Filanovsky I M, Allam A, Fernandes J R 2008 IEEE International Symposium on Circuits and Systems Washington, USA, May 18–21, 2008 p2322
[33] Xu Y M, Yao Z, Hobiny A, Aatef H, Ma J 2019 Front. Inform. Tech. El. 20 571
Google Scholar
[34] Ma J, Lv M, Zhou P, Xu Y, Hayat T 2017 Appl. Math. Comput. 307 321
Google Scholar
[35] Qin H L, Ma J, Ren G D, Zhou P 2018 Int J. Mod. Phys. B 32 1850298
Google Scholar
[36] An X L, Zhang L 2018 Nonlinear Dyn. 94 2995
Google Scholar
[37] Varshney V, Sabarathinam S, Prasad A 2018 Int. J. Bifurcat. Chaos 28 1850013
Google Scholar
[38] Dudkowski D, Jafari S, Kapitaniak T, Kuznetsov N, Leonov G, Prasad A 2016 Phys. Rep. 637 1
Google Scholar
[39] Gallas J A C 2015 Mod. Phys. Lett. B 29 1530018
Google Scholar
[40] Rosa L A S, Prebianca F, Hoff A, Manchein C, Albuquerque H A 2020 Int. J. Bifurcat. Chaos 30 118
Google Scholar
[41] Rao X B, Chu Y D, Chang Y X, Zhang J G, Tian Y P 2017 Nonlinear Dyn. 88 2347
Google Scholar
[42] Desroches M, Guckenheimer J, Krauskopf B, Kuehn C, Hinke M O, Wechselberger M 2012 SIAM Rev. 54 211
Google Scholar
[43] Kousaka T, Ogura Y, Shimizu K, Asahara H, Inaba N 2017 Physica D 27 48
Google Scholar
[44] Wang Q Q, Yu Y, Zhang Z D, Han X J 2019 J. Low Freq. Noise. V. A. 38 377
Google Scholar
[45] Rotstein H G 2014 Encyclopedia of Computational Neuroscience 2 1
Google Scholar
[46] 孙常春, 陈仲堂, 侯祥林 2017 振动与冲击 36 220
Sun C C, Chen Z T, Hou X L 2017 J. Vib. Shock 36 220
-
图 2 EMFN模型(2)的时间响应图和吸引子 (a)
${P_1}$ 附近的共存振荡; (b) 图(a)中蓝色放大图; (c)${P_1}$ 附近的周期2极限环; (d)${P_2}$ 附近的共存振荡; (e) 图(d)中蓝色放大图; (f)${P_2}$ 附近的周期2极限环; (g)${P_3}$ 附近的共存振荡; (h) 图(g)中蓝色放大图; (i)${P_3}$ 附近的周期1极限环Fig. 2. Time responses and attractors of EMFN model (2): (a) Coexistence oscillation near
${P_1}$ ; (b) enlargement of the blue in (a); (c) limit cycle with period-2 near${P_1}$ ; (d) coexistence oscillation near${P_2}$ ; (e) enlargement of the blue in (d); (f) limit cycle with period-2 near${P_2}$ ; (g) coexistence oscillation near${P_3}$ ; (h) enlargement of the blue in (g); (i) limit cycle with period-1 near${P_3}$ .
图 3 EMFN模型(2)的吸引域 (a), (c)和(e)是外界刺激电流分别取
${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ 时x-y上的吸引域; (b), (d)和(f)是外界刺激电流分别取${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ 时x-ϕ上的吸引域Fig. 3. The attractive basins of EMFN model (2): (a), (c) and (e) are the attractive basins in x-y plane under
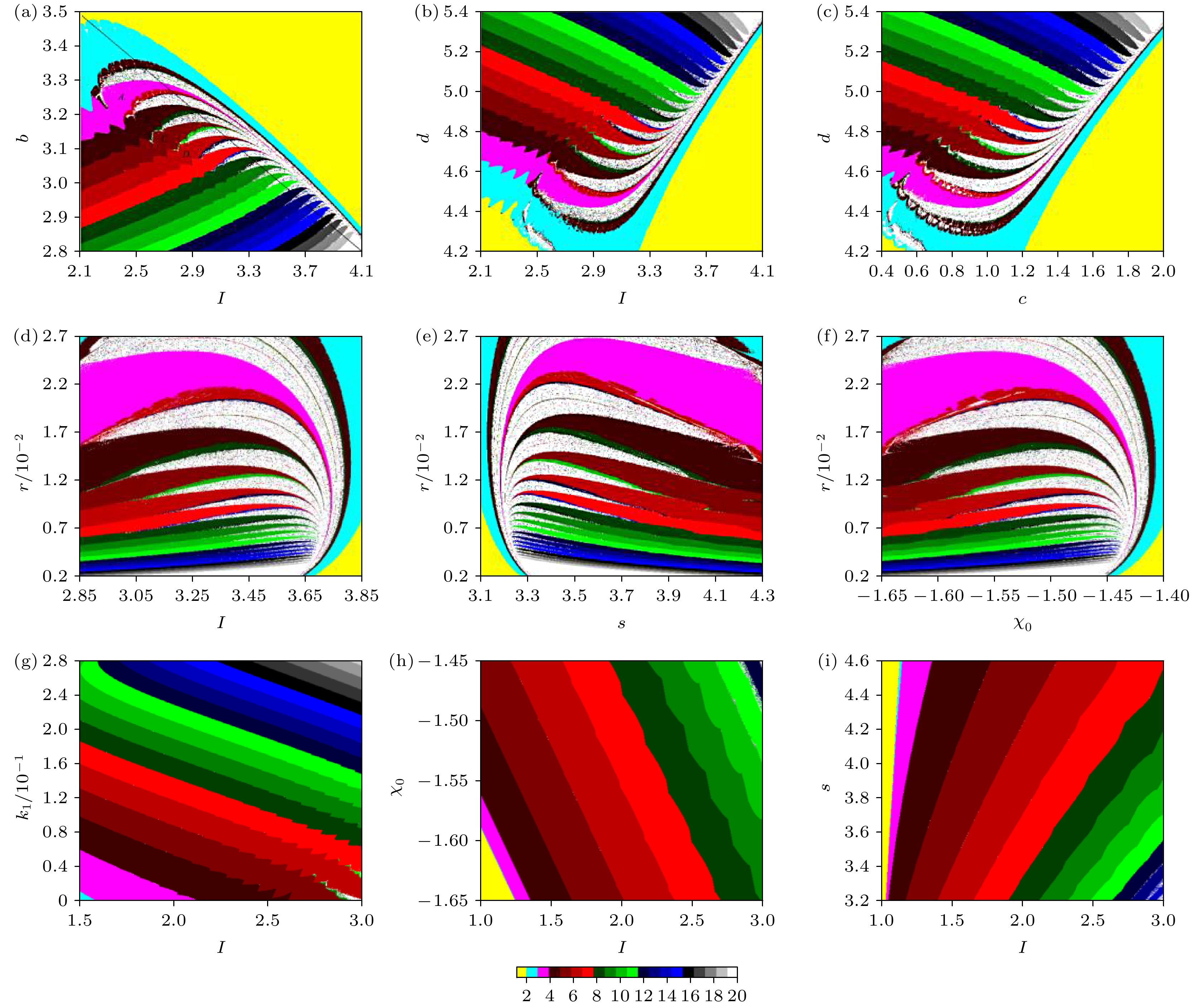
${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ , respectively; (b), (d) and (f) are the attractive basins in x-ϕ plane under${I_{\rm{1}}}, \;{I_2}, \;{I_3}$ , respectively.
图 4 EMFN模型(2)关于x的双参数分岔图 (a)
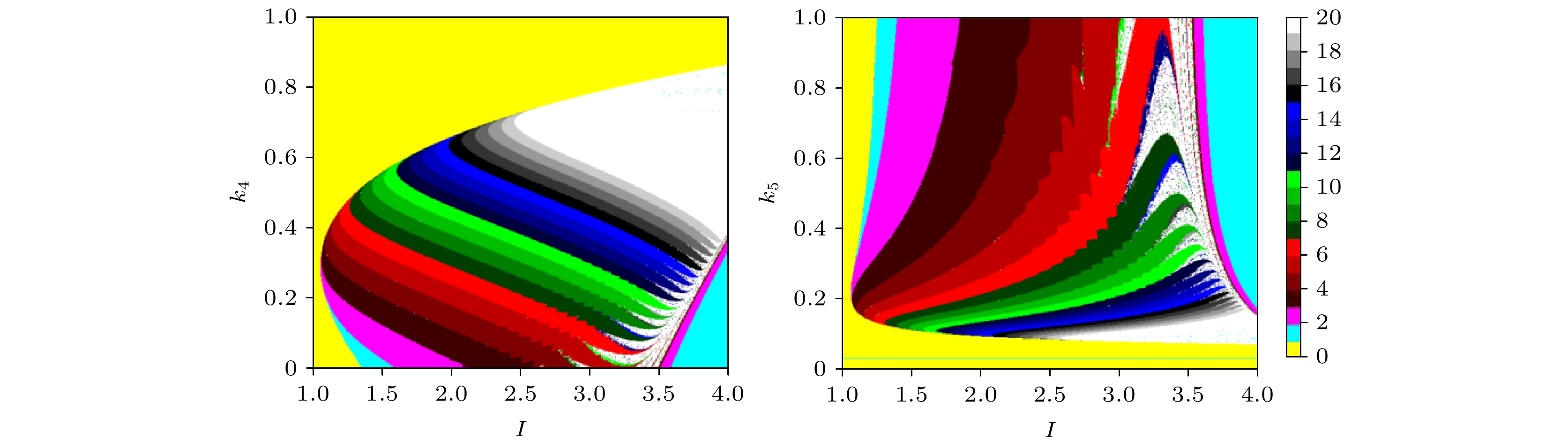
$I$ 和$b$ 对应的分岔图; (b)$I$ 和$d$ 对应的分岔图; (c)$c$ 和$d$ 对应的分岔图; (d)$I$ 和$r$ 对应的分岔图; (e)$s$ 和$r$ 对应的分岔图; (f)${\chi _0}$ 和$r$ 对应的分岔图; (g)$I$ 和${k_1}$ 对应的分岔图; (h)$I$ 和${\chi _0}$ 对应的分岔图; (i)$I$ 和$s$ 对应的分岔图Fig. 4. Two-parameter bifurcation diagrams of EMFN model (2) versus x: (a) Bifurcation diagram versus
$I$ and$b$ ; (b) bifurcation diagram versus$I$ and$d$ ; (c) bifurcation diagram versus$c$ and$d$ ; (d) bifurcation diagram versus$I$ and$r$ ; (e) bifurcation diagram versus$s$ and$r$ ; (f) bifurcation diagram versus${\chi _0}$ and$r$ ; (g) bifurcation diagram versus$I$ and${k_1}$ ; (h) bifurcation diagram versus$I$ and${\chi _0}$ ; (i) bifurcation diagram versus$I$ and$s$ .
图 5 关于
$I$ 的ISI分岔图和单参分岔图 (a) ISI 分岔图; (b) 单参分岔图Fig. 5. ISI bifurcation and one-parameter bifurcation versus I : (a) ISI bifurcation; (b) one-parameter bifurcation.
图 7 EMFN模型(2)关于
$I$ 和$b$ 的时间响应图 (a)$I = 2.389, b = 3.239$ 时的周期3簇放电; (b)$I = 2.577, b = 3.173$ 时的周期4簇放电; (c)$I = 2.733, b = 3.134$ 时的周期5簇放电; (d)$I = 2.898, b = 3.093$ 时的周期6簇放电Fig. 7. Time response diagram of EMFN model (2) versus
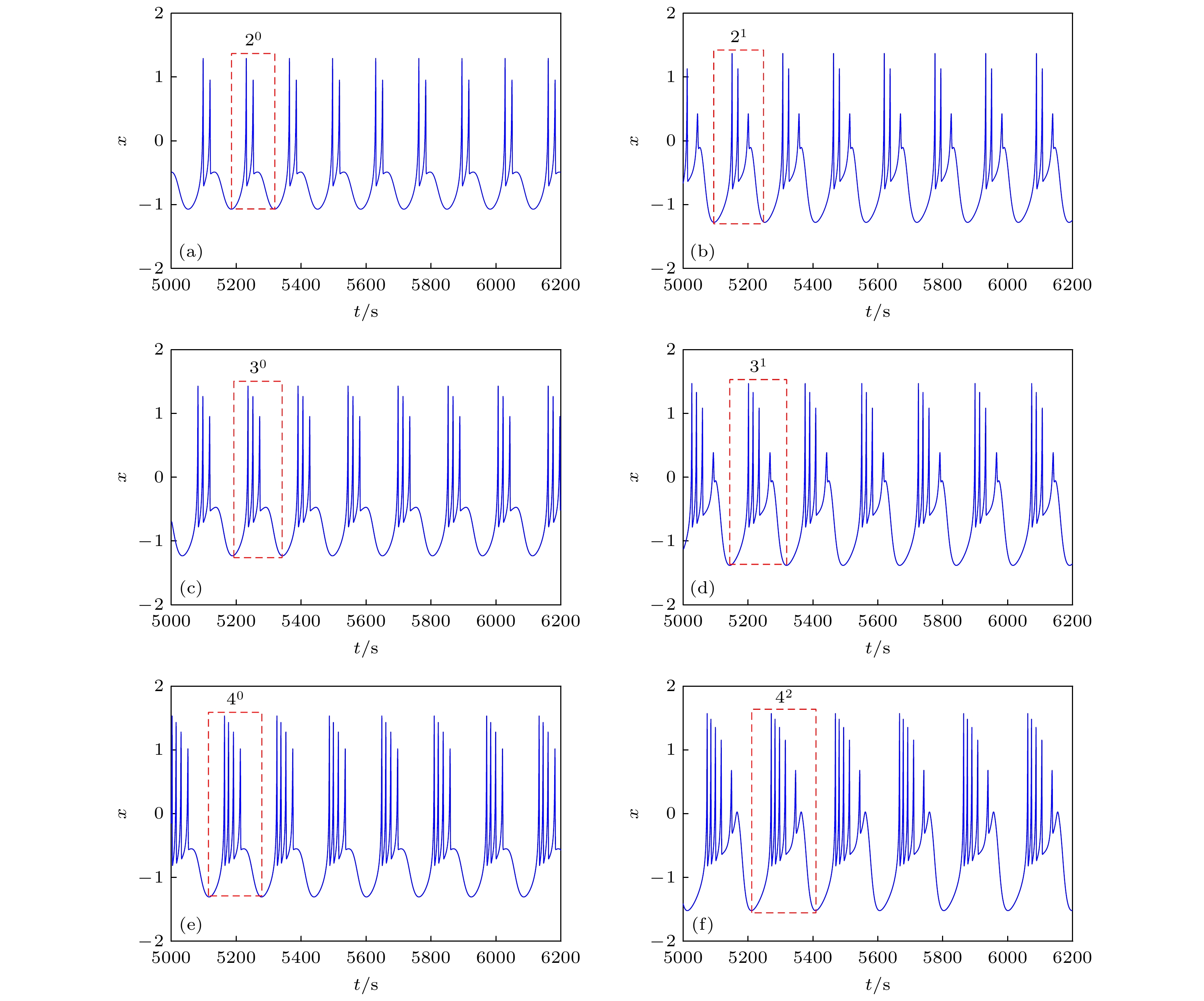
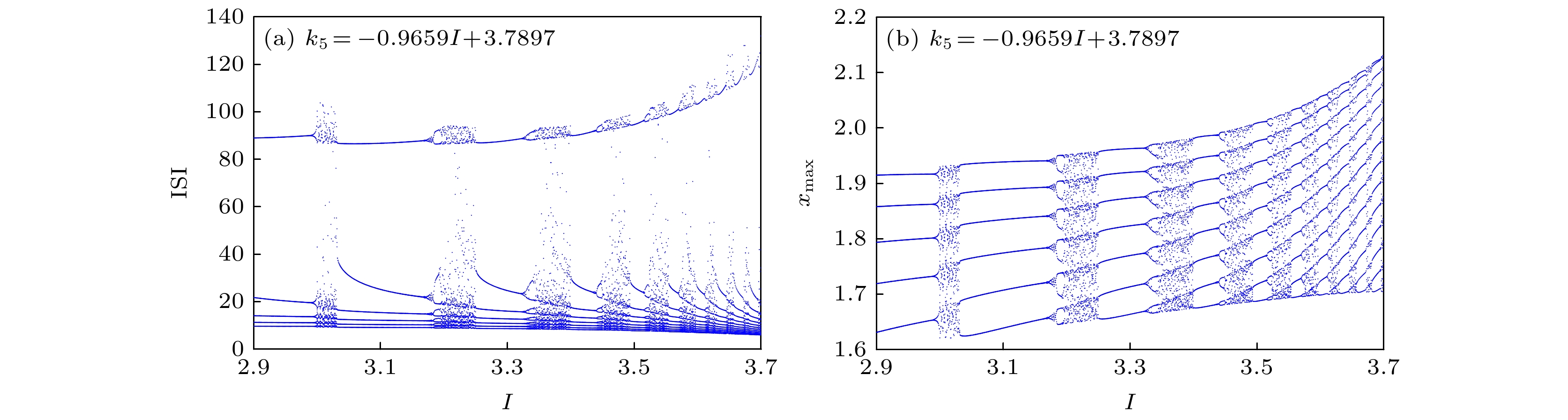
$I$ and$b$ : (a) Bursting with period-3 when$I = 2.389, b = 3.239$ ; (b) bursting with period-4 when$I = 2.577, b = 3.173$ ; (c) bursting with period-5 when$I = 2.733, b = 3.134$ ; (d) bursting with period-6 when$I = 2.898, b = 3.093$ .
图 9 EMFN模型(2)的时间响应图 (a) 周期2放电; (b) 周期
${2^1}$ 放电; (c) 周期3放电; (d) 周期${3^1}$ 放电; (e) 周期4放电; (f) 周期${{\rm{4}}^{\rm{2}}}$ 放电Fig. 9. Time response diagrams of EMFN model (2): (a) Discharge with period-2; (b) discharge with period-
${2^1}$ ; (c) discharge with period-3; (d) discharge with period-${3^1}$ ; (e) discharge with period-4; (f) discharge with period-${4^2}$ .
图 10 EMFN模型(2)的共存吸引域 (a)
$({k_0}, d) = (0.6587, 4.2596)$ 时关于x-ϕ的吸引域; (b)$({k_0}, d) = (0.6587, 4.2596)$ 时关于x-E的吸引域; (c)$({k_0}, d) = (0.7032, 4.3758)$ 时关于x-ϕ的吸引域; (d)$({k_0}, d) = (0.7032, 4.3758)$ 时关x-E于的吸引域; (e)$({k_0}, d) = (0.7{\rm{123}}, 4.{\rm{5032}})$ 时关于x-ϕ的吸引域; (f)$({k_0}, d) = (0.7{\rm{123}}, 4.{\rm{5032}})$ 时关于x-E的吸引域Fig. 10. The coexisting attraction domains of EMFN model (2): (a) Attractive basins of x-ϕ plane when
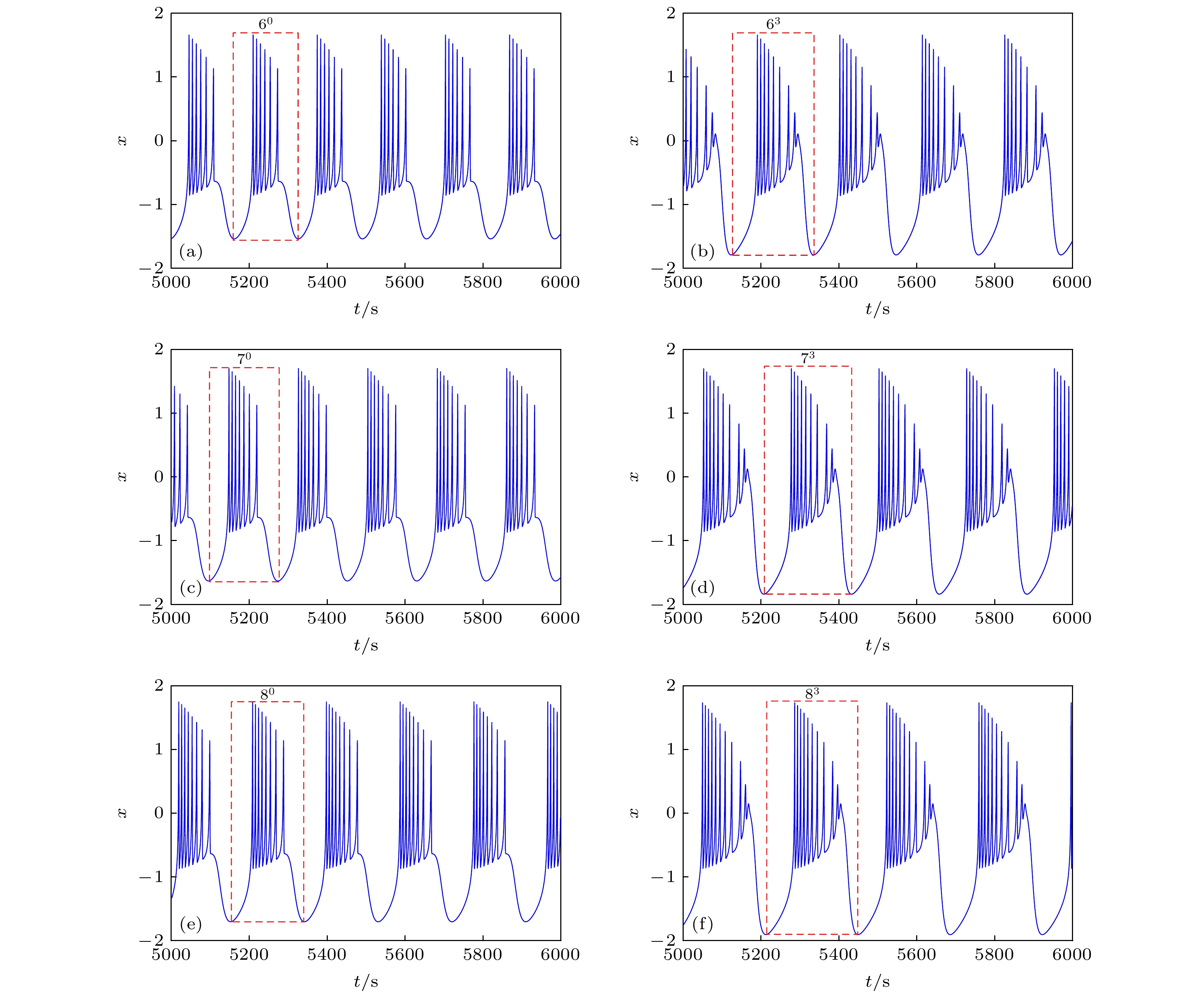
$({k_0}, d) = (0.6587, 4.2596)$ ; (b) attractive basins of x-E plane when$({k_0}, d) = (0.6587, 4.2596)$ ; (c) attractive basins of x-ϕ plane when$({k_0}, d) = (0.7032, 4.3758)$ ; (d) attractive basins of x-E plane when$({k_0}, d) = (0.7032, 4.3758)$ ; (e) attractive basins of x-ϕ plane when$({k_0}, d) = (0.7123, 4.5032)$ ; (f) attractive basins of x-E plane when$({k_0}, d) = (0.7123, 4.5032)$ .
图 11 关于
${k_0}$ 的ISI分岔图和单参分岔图 (a) ISI 分岔图; (b) 单参分岔图Fig. 11. ISI bifurcation and one-parameter bifurcation versus
${k_0}$ : (a) ISI bifurcation; (b) one-parameter bifurcation.
图 13 膜电压的发放数关于参数
${k_0}$ 变化图Fig. 13. The change of spike count of membrane voltage versus parameter
${k_0}$ .
图 15 EMFN模型(2)的时间响应图 (a) 周期6放电; (b) 周期
${6^3}$ 放电; (c) 周期7放电; (d) 周期${7^3}$ 放电; (e) 周期8放电; (f) 周期${8^3}$ 放电Fig. 15. Time response diagrams of EMFN model (2): (a) Discharge with period-6; (b) discharge with period-
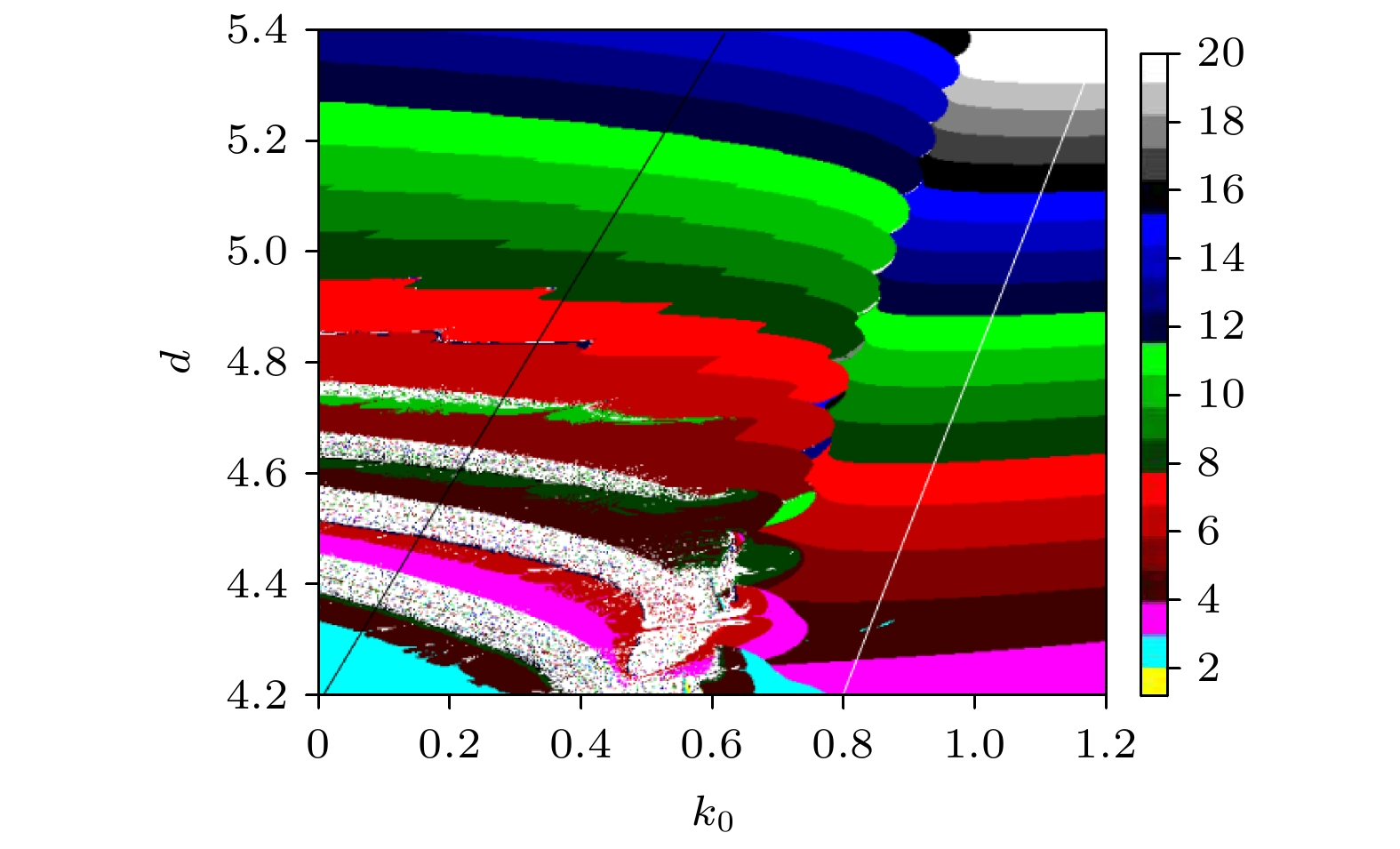
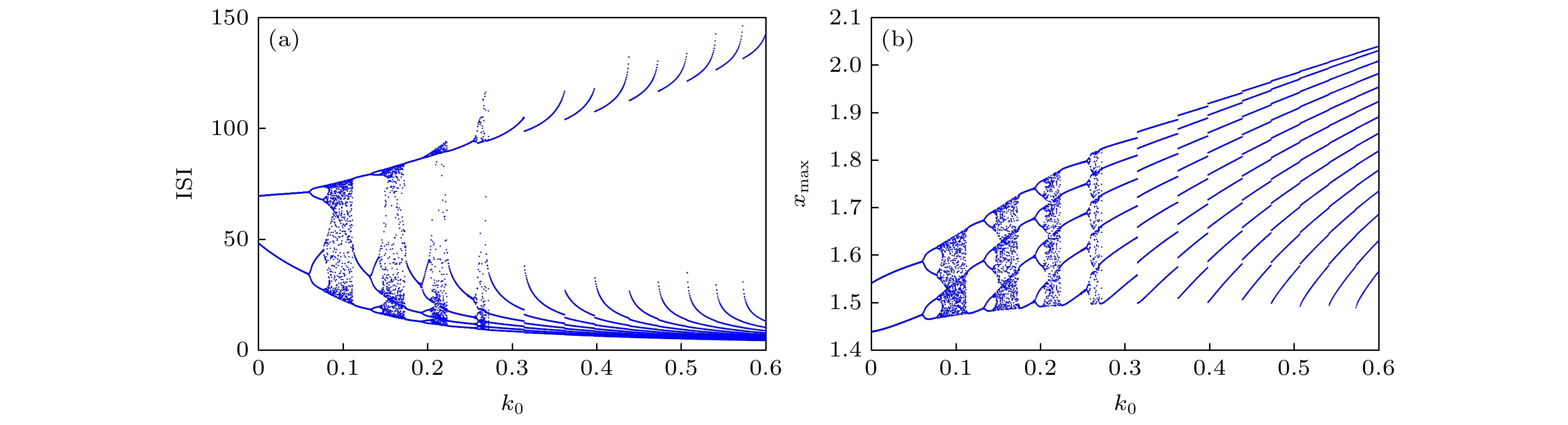
${6^3}$ ; (c) discharge with period-7; (d) discharge with period-${7^3}$ ; (e) discharge with period-8; (f) discharge with period-${8^3}$ .
图 16 关于
${k_0}$ 的 ISI 分岔图和单参分岔图Fig. 16. ISI bifurcation and one-parameter bifurcation versus
${k_0}$ .
图 17 膜电压的发放数关于参数
${k_0}$ 变化图Fig. 17. The change of spike count of membrane voltage versus parameter
${k_0}$ .
图 21 反馈增益
$m$ 对受控系统(7)的放电影响 (a) 当$I = {I_2}$ 时, 受控系统(7)放电演化图; (b) 当$I = {I_3}$ 时, 受控系统(7)放电演化图Fig. 21. The discharge influence of feedback gain
$m$ to controlled system (7): (a) Discharge evolution of the controlled system (7) when$I = {I_2}$ ; (b) Discharge evolution of the controlled system (7) when$I = {I_3}$ . -
[1] Varona P, Levi R, Arshavsky Y I, Rabinovich M I, Selverston A I 2004 Neurocomputing 58 549
Google Scholar
[2] Kato R, Yamanaka M, Kobayashi M 2018 J. Pharmacol. Sci. 136 172
Google Scholar
[3] Kayasandik C, Guo K H, Labate D 2019 J. Comput. Appl. Math. 349 482
Google Scholar
[4] 丁学利, 贾冰, 李玉叶 2019 68 180502
Google Scholar
Ding X L, Jia B, Li Y Y 2019 Acta Phys. Sin. 68 180502
Google Scholar
[5] Nielsen B F 2017 J. Math. Neurosci. 7 6
Google Scholar
[6] Shim Y, Husbands P 2018 Adapt. Behav. 26 165
Google Scholar
[7] Otsuka S, Omori T 2019 Neural Netw. 109 137
Google Scholar
[8] 杨永霞, 李玉叶, 古华光 2020 69 040501
Google Scholar
Yang Y X, Li Y Y, Gu H G 2020 Acta Phys. Sin. 69 040501
Google Scholar
[9] Hodgkin A L, Huxley A F 1952 J. Physiol. 116 473
Google Scholar
[10] Morris C, Lecar H 1981 Biophys. J. 35 193
Google Scholar
[11] Chay R T 1983 J. Phys. Chem. 87 2935
Google Scholar
[12] Hindmarsh J L, Rose R M 1984 P. Roy. Soc. B-Biol. Sci. 221 87
Google Scholar
[13] Izhikevich E M 2003 IEEE T. Neural Networ. 14 1569
Google Scholar
[14] FitzHugh R 1961 Biophys. J. 1 445
Google Scholar
[15] Cassidy A S, Merolla P, Arthur J V, Esser S K, Jackson B, Alvarez-Icaza R, Datta P, Sawada J, Wong T M, Feldman V, Amir A, Rubin D B, Akopyan F, McQuinn E, Risk W P, Modha D S 2013 The 2013 International Joint Conference on Neural Networks Dallas, USA, August 4–9, 2013 p1
[16] 徐泠风, 李传东, 陈玲 2016 65 240701
Google Scholar
Xu L F, Li C D, Chen L 2016 Acta Phys. Sin. 65 240701
Google Scholar
[17] Barrio R, Lefranc M, Martínez M A, Serrano S 2015 Europhyslett. Lett. 109 20002
Google Scholar
[18] Yang S M, Wang J, Li S, Li H Y, Wei X L, Yu H T, Deng B 2015 Neurocomputing 177 274
Google Scholar
[19] Babacan Y, Kaçar F, Gürkan K 2016 Neurocomputing 203 86
Google Scholar
[20] Bao B C, Huang A H, Bao H 2018 Complexity 2018 1
Google Scholar
[21] Usha K, Subha P A 2019 Biosystems 5 1
Google Scholar
[22] Zhao Y, Sun X Y, Liu Yang, Kurths J 2018 Nonlinear Dyn. 93 1315
Google Scholar
[23] Pham V T, Jafari S, Vaidyanathan S, Vilos C, Wang X 2016 Sci. China Technol. Sci. 59 358
Google Scholar
[24] Ma J, Tang J 2015 Sci. China Technol. Sci. 58 2038
Google Scholar
[25] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
Google Scholar
[26] Wu F Q, Wang C N, Jin W Y Ma J 2017 Physica A 469 81
Google Scholar
[27] Kafraja M S, Parastesha F, Jafariba S 2020 Chaos, Soliton. Fract. 137 109782
Google Scholar
[28] 安新磊, 张莉 2020 力学学报 52 1174
Google Scholar
An X L, Zhang L 2020 Chin. J. Theor. Appl. Mech. 52 1174
Google Scholar
[29] Ma J, Zhang G, Hayat T, Ren G D 2019 Nonlinear Dyn. 95 1585
Google Scholar
[30] Du L, Cao Z L, Lei Y M, Deng Z C 2019 Sci. China Technol. Sci. 62 1141
Google Scholar
[31] Wang C N, Tang J, Ma J 2019 Eur. Phys. J-Spec. Top. 228 1907
Google Scholar
[32] Oliveira L B, Filanovsky I M, Allam A, Fernandes J R 2008 IEEE International Symposium on Circuits and Systems Washington, USA, May 18–21, 2008 p2322
[33] Xu Y M, Yao Z, Hobiny A, Aatef H, Ma J 2019 Front. Inform. Tech. El. 20 571
Google Scholar
[34] Ma J, Lv M, Zhou P, Xu Y, Hayat T 2017 Appl. Math. Comput. 307 321
Google Scholar
[35] Qin H L, Ma J, Ren G D, Zhou P 2018 Int J. Mod. Phys. B 32 1850298
Google Scholar
[36] An X L, Zhang L 2018 Nonlinear Dyn. 94 2995
Google Scholar
[37] Varshney V, Sabarathinam S, Prasad A 2018 Int. J. Bifurcat. Chaos 28 1850013
Google Scholar
[38] Dudkowski D, Jafari S, Kapitaniak T, Kuznetsov N, Leonov G, Prasad A 2016 Phys. Rep. 637 1
Google Scholar
[39] Gallas J A C 2015 Mod. Phys. Lett. B 29 1530018
Google Scholar
[40] Rosa L A S, Prebianca F, Hoff A, Manchein C, Albuquerque H A 2020 Int. J. Bifurcat. Chaos 30 118
Google Scholar
[41] Rao X B, Chu Y D, Chang Y X, Zhang J G, Tian Y P 2017 Nonlinear Dyn. 88 2347
Google Scholar
[42] Desroches M, Guckenheimer J, Krauskopf B, Kuehn C, Hinke M O, Wechselberger M 2012 SIAM Rev. 54 211
Google Scholar
[43] Kousaka T, Ogura Y, Shimizu K, Asahara H, Inaba N 2017 Physica D 27 48
Google Scholar
[44] Wang Q Q, Yu Y, Zhang Z D, Han X J 2019 J. Low Freq. Noise. V. A. 38 377
Google Scholar
[45] Rotstein H G 2014 Encyclopedia of Computational Neuroscience 2 1
Google Scholar
[46] 孙常春, 陈仲堂, 侯祥林 2017 振动与冲击 36 220
Sun C C, Chen Z T, Hou X L 2017 J. Vib. Shock 36 220
下载:
计量
- 文章访问数: 7714
- PDF下载量: 134
- 被引次数: 0
