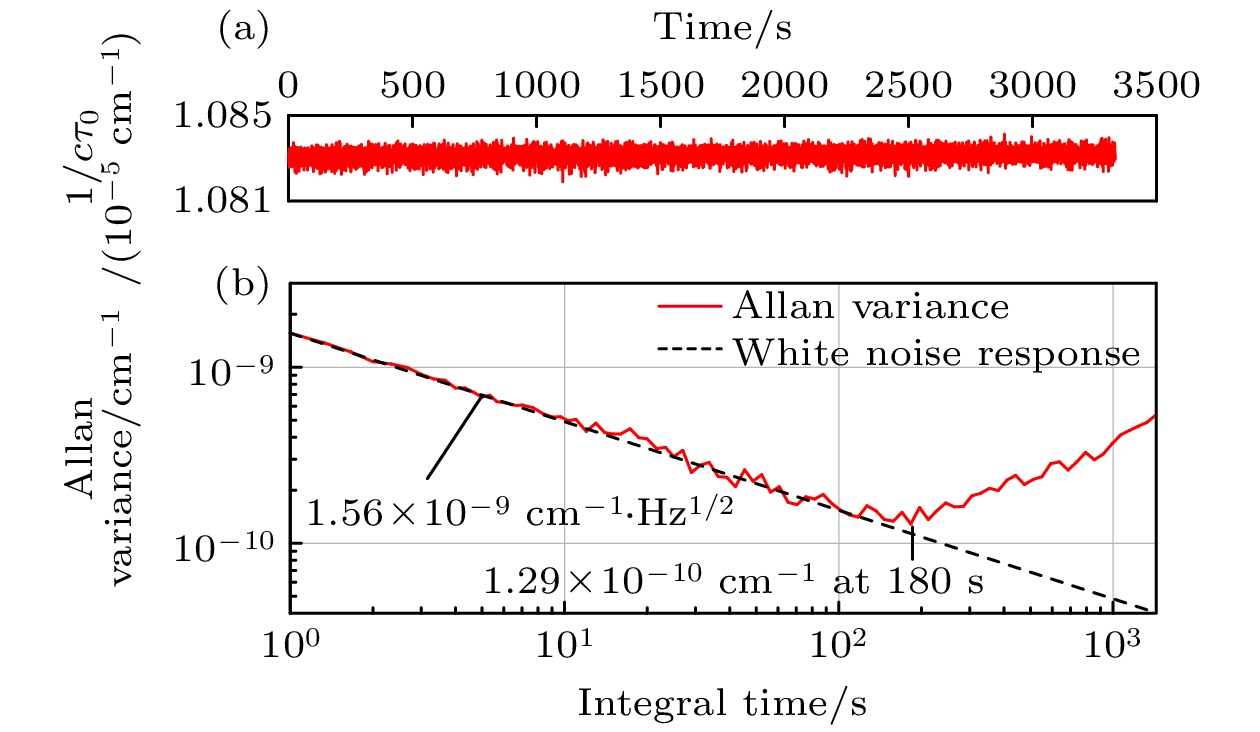
-
腔衰荡光谱技术是一种高灵敏的腔增强分子吸收光谱测量技术, 由于激光频率噪声大, 导致激光到腔耦合效率低, 严重限制了其对痕量气体的探测灵敏度. 光学反馈可以有效压窄半导体激光器的线宽, 提高激光到外部谐振腔的耦合效率. 本文基于精细度为7800的Fabry-Pérot腔, 发展了光学反馈线性腔衰荡光谱技术. 首先从光场相位的角度给出了线性腔光学反馈的原理, 然后分析了影响测量不确定性的因素, 包括光学反馈率、衰荡信号触发阈值、探测器相对透射汇聚光斑位置等. 实验结果表明, 通过设置低反馈率(3%自由光谱区间)、高衰荡信号触发阈值(90%腔模幅度)以及将光斑聚焦到探测器有效面中心等措施, 结合光学反馈效应, 可将空腔衰荡时间的相对不确定度提升至0.026%, 远优于传统腔衰荡技术获得的典型值. 系统在积分时间为180 s时, 获得探测灵敏度为1.3 × 10–10 cm–1, 对应甲烷的最小可探测吸收体积浓度为0.35 × 10–9, 从而满足了碳监测的要求.Cavity ring-down spectroscopy (CRDS) is a highly sensitive molecular absorption spectroscopic technology, which has been widely used in mirror reflectance measurement, atmospheric trace gas detection, molecular precision spectroscopy and other fields. It deduces the intracavity absorption by measuring the rapid variation of the ringdown signal. As a result, detector with high linearity, broad bandwidth and low electrical noise is indispensable. Additionally, owing to the large noise in laser frequency, low laser-to-cavity coupling efficiency is obtained. Consequently, the cavity transmission is faint, which deteriorates the detection sensitivity. Optical feedback can address this problem by locking the laser to the cavity longitudinal mode. Then, the laser frequency noise is suppressed and hence better detection sensitivity is expected. Optical feedback CRDS with V-shape cavity has been widely studied. Compared with Fabry-Perot cavity, this cavity geometry is very sensitive to mechanical vibration and possesses low degree of fineness due to an additional mirror. In this paper, optical feedback linear cavity ring-down spectroscopy based on a Fabry-Perot cavity with a degree of fineness of 7800 is presented. The principle of the combination of optical feedback and linear cavity is explained from the perspective of the light phase, which shows that the reflection will not generate efficient optical feedback if the feedback phase is appropriately controlled and laser to cavity locking can be therefore realized. And then, the factors influencing the stability of ring-down signal are analyzed, including the feedback ratio, the trigger voltage for the ringdown event, and the distance between the light spot and the detector center. The experimental results show that a superior fractional uncertainty of the empty ringdown time of 0.026% can be obtained with a low feedback rate (3% FSR), a high ringdown signal trigger threshold (90% cavity mode amplitude) and superposition of the light spot with the detector center. With Allan variance analysis, the white noise response of 1.6 × 10–9 cm–1·Hz–1/2 and the detection sensitivity of 1.3 × 10–10 cm–1 for trace gas detection can be achieved in an integration time of 180 s, corresponding to the lowest CH4 concentration detection of 0.35 × 10–9 at 6046.9 cm–1. This robust spectroscopic technique paves the way for constructing high-sensitive and stable-cavity based instrument for trace gas detection.
-
Keywords:
- optical feedback /
- cavity ringdown /
- linear cavity /
- high sensitivity
更正: 光学反馈线性腔衰荡光谱技术不确定性 [ 2022, 71(12): 124201]
王兴平, 赵刚, 焦康, 陈兵, 阚瑞峰, 刘建国, 马维光. 光学反馈线性腔衰荡光谱技术不确定性. , 2022, 71(15): 159901. doi: 10.7498/aps.71.159901
[1] Paldus B A, Kachanov A A 2005 Can. J. Phys. 83 975
Google Scholar
[2] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p4
[3] Abhijit M, Sanchi M, Manik P 2021 Anal. Chem. 93 388
Google Scholar
[4] Crawford T M 1985 Proc. SPIE 540 295
Google Scholar
[5] Sridhar G, Agarwalla S K, Singh S, Gantayet L 2010 Pramana J. Phys. 75 1233
Google Scholar
[6] Xiao S L, Li B C, Wang J 2020 Metrologia 57 055002
Google Scholar
[7] McHale L E, Hecobian A, Yalin A P 2016 Opt. Express 24 5523
Google Scholar
[8] Kleine D, Mürtz M, Lauterbach J, Dahnke H, Urban W, Hering P, Kleinermanns K 2 2001 Isr. J. Chem. 41 111
Google Scholar
[9] Cui L H, Yan C X 2016 Chem. Eng. Trans. 55 169
Google Scholar
[10] Kleine D, Lauterbach J, Kleinermanns K, Hering P 2001 Appl. Phys. B 72 249
Google Scholar
[11] 康鹏, 孙羽, 王进, 刘安雯, 胡水明 2018 67 104206
Google Scholar
Kang P, Sun Y, Wang J, Liu A W, Hu S M 2018 Acta Phys. Sin. 67 104206
Google Scholar
[12] Mikhailenko S N, Le W, Kassi S, Campargue A 2007 J. Mol. Spectrosc. 244 170
Google Scholar
[13] Winkler G, Perner L W, Truong G W, Zhao G, Bachmann D, Mayer A S, Fellinger J, Follman D, Heu P, Deutsch C, Bailey D M, Peelaers H, Puchegger S, Fleisher A J, Cole G D, Heckl O H 2021 Optica 8 686
Google Scholar
[14] Cole G D, Zhang W, Martin M J, Ye J, Aspelmeyer M 2013 Nat. Photonics 7 644
Google Scholar
[15] AlMulla M, Liu J M 2020 Opt. express 28 14677
Google Scholar
[16] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97
Google Scholar
[17] Laurent P, Clairon A, Breant C 1989 IEEE J. Quantum Electron. 25 1131
Google Scholar
[18] Morville J, Kassi S, Chenevier M, Romanini D 2005 Appl. Phys. B 80 1027
Google Scholar
[19] Dahmani B, Hollberg L, Drullinger R 1987 Opt. Lett. 12 876
Google Scholar
[20] Kassi S, Burkart J 2015 Appl. Phys. B 119 97
Google Scholar
[21] Ye J, Ma L S, Hall J L 1998 J. Opt. Soc. Am. B 15 6
Google Scholar
[22] Zhao G, Thomas H, Ma W, Ove A 2018 Opt. Lett. 43 715
Google Scholar
[23] Morville J, Romanini D, Kachanov A A, Chenevier M, 2004 Appl. Phys. B 78 465
Google Scholar
[24] Tian J F, Zhao G, Fleisher A J, Ma W G, Jia S T 2021 Opt. Express 29 26831
Google Scholar
[25] Zhao G, Tian J F, Hodges J T, Fleisher A J 2021 Opt. Lett. 46 3057
Google Scholar
[26] Wang X P, Zhao G, Jiao K, Chen B, Kan R F, Cao Z H, Liu J G, Ma W G 2022 Front. Phys. 10 857371
Google Scholar
[27] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p180
[28] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p29
[29] Brown S S, Wilson R W, Ravishankara A R, 2000 J. Phys. Chem. A 104 4976
Google Scholar
[30] Zee R, Hodges J T, Looney J P, 1999 Appl. Opt. 38 3951
Google Scholar
[31] Huang H, Lehmann K K, 2010 Appl. Opt. 49 1378
Google Scholar
[32] Cao Z S, Li Z X, Xu F, Wu Y Q, Zhou Z X, Tong Z M, Ma W G, Zhu W Y 2019 Sensors 19 5232
Google Scholar
[33] Werle P, Mücke R, Slemr F 1993 Appl. Phys. B 57 131
Google Scholar
[34] Gordon I E, Rothman L S, Hill C, et al. 2017 J. Quant. Spectrosc. Radiat. Transfer 203 3
Google Scholar
-
图 1 直接反射光与腔内泄漏光在线性腔光学反馈系统中的光路示意图
Fig. 1. Schematic diagram of light path of direct reflected light and cavity leakage light in linear cavity based optical feedback system.
图 2 光学反馈线性腔衰荡系统装置图
Fig. 2. Diagram of experimental setup for optical feedback linear cavity ring-down spectroscopy.
图 3 (a) 腔透射信号(黑线)与触发信号(红线); (b) 为(a)图中蓝色方框的放大图
Fig. 3. (a) Cavity transmission signal (black line) and trigger signal (red line); (b) an enlarged view of the blue box in Figure (a).
图 4 (a)理论计算得到的不同光学反馈率下的频率锁定范围; (b)实验测得不同反馈率下的腔透射信号
Fig. 4. (a) Theoretical calculation results of frequency locking range under different optical feedback ratio; (b) measured cavity transmission signals under different feedback ratio.
图 5 不同频率锁定范围下的空腔衰荡时间相对不确定度
Fig. 5. Fractional uncertainty of empty cavity ring-down time at different frequency locking ranges.
图 6 腔透射信号的(a) Y轴和(b) X轴方向光强分布
Fig. 6. Light intensity distribution of the transmitted cavity signal in (a) Y-axis and (b) X-axis direction.
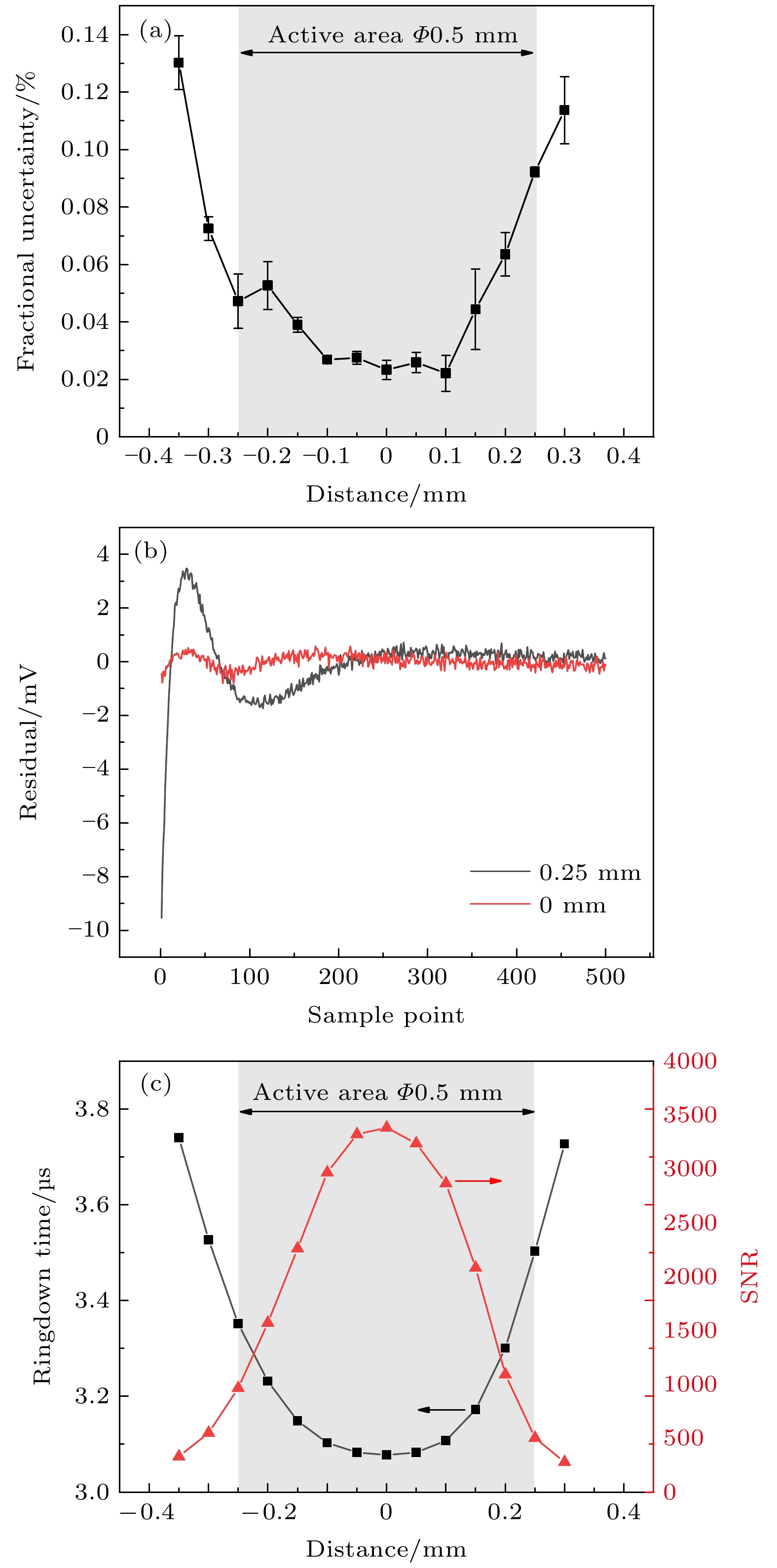
图 7 透射光在探测器不同有效面位置上的实验结果 (a) 空腔衰荡时间相对不确定度; (b) 不同探测器位置下的衰荡信号拟合残差; (c) 衰荡时间 (黑色曲线) 及衰荡信号拟合信噪比 (红色曲线).
Fig. 7. Experimental results of transmitted light at different positions of detector’s effective surface. (a) Fractional uncertainty of cavity ring-down time (black line); (b) ring-down signal fitting residuals at different detector positions; (c) ring-down time and signal-to-noise ratio of ring-down signal fitting (red line) as a function of the distance between the light and the detector center.
图 8 不同衰荡信号触发阈值条件下的空腔衰荡时间相对不确定度和衰荡信号拟合信噪比
Fig. 8. Fractional uncertainty of cavity ring-down time and signal-to-noise ratio (SNR) under different trigger thresholds of ring-down signals.
图 9 空腔衰荡时间的长期测量(a)和Allan方差分析(b), 黑色点线为白噪声响应曲线, 红色曲线为Allan方差
Fig. 9. Long-term measurement of cavity ring-down time (a) and Allan variance analysis (b). The black dotted line is the white noise response curve, and the red curve is the Allan variance.
图 10 (a)大气甲烷吸收测量以及拟合结果; (b)拟合残差
Fig. 10. (a) Atmospheric methane absorption measurement and fitting results; (b) fitting residual.
-
[1] Paldus B A, Kachanov A A 2005 Can. J. Phys. 83 975
Google Scholar
[2] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p4
[3] Abhijit M, Sanchi M, Manik P 2021 Anal. Chem. 93 388
Google Scholar
[4] Crawford T M 1985 Proc. SPIE 540 295
Google Scholar
[5] Sridhar G, Agarwalla S K, Singh S, Gantayet L 2010 Pramana J. Phys. 75 1233
Google Scholar
[6] Xiao S L, Li B C, Wang J 2020 Metrologia 57 055002
Google Scholar
[7] McHale L E, Hecobian A, Yalin A P 2016 Opt. Express 24 5523
Google Scholar
[8] Kleine D, Mürtz M, Lauterbach J, Dahnke H, Urban W, Hering P, Kleinermanns K 2 2001 Isr. J. Chem. 41 111
Google Scholar
[9] Cui L H, Yan C X 2016 Chem. Eng. Trans. 55 169
Google Scholar
[10] Kleine D, Lauterbach J, Kleinermanns K, Hering P 2001 Appl. Phys. B 72 249
Google Scholar
[11] 康鹏, 孙羽, 王进, 刘安雯, 胡水明 2018 67 104206
Google Scholar
Kang P, Sun Y, Wang J, Liu A W, Hu S M 2018 Acta Phys. Sin. 67 104206
Google Scholar
[12] Mikhailenko S N, Le W, Kassi S, Campargue A 2007 J. Mol. Spectrosc. 244 170
Google Scholar
[13] Winkler G, Perner L W, Truong G W, Zhao G, Bachmann D, Mayer A S, Fellinger J, Follman D, Heu P, Deutsch C, Bailey D M, Peelaers H, Puchegger S, Fleisher A J, Cole G D, Heckl O H 2021 Optica 8 686
Google Scholar
[14] Cole G D, Zhang W, Martin M J, Ye J, Aspelmeyer M 2013 Nat. Photonics 7 644
Google Scholar
[15] AlMulla M, Liu J M 2020 Opt. express 28 14677
Google Scholar
[16] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97
Google Scholar
[17] Laurent P, Clairon A, Breant C 1989 IEEE J. Quantum Electron. 25 1131
Google Scholar
[18] Morville J, Kassi S, Chenevier M, Romanini D 2005 Appl. Phys. B 80 1027
Google Scholar
[19] Dahmani B, Hollberg L, Drullinger R 1987 Opt. Lett. 12 876
Google Scholar
[20] Kassi S, Burkart J 2015 Appl. Phys. B 119 97
Google Scholar
[21] Ye J, Ma L S, Hall J L 1998 J. Opt. Soc. Am. B 15 6
Google Scholar
[22] Zhao G, Thomas H, Ma W, Ove A 2018 Opt. Lett. 43 715
Google Scholar
[23] Morville J, Romanini D, Kachanov A A, Chenevier M, 2004 Appl. Phys. B 78 465
Google Scholar
[24] Tian J F, Zhao G, Fleisher A J, Ma W G, Jia S T 2021 Opt. Express 29 26831
Google Scholar
[25] Zhao G, Tian J F, Hodges J T, Fleisher A J 2021 Opt. Lett. 46 3057
Google Scholar
[26] Wang X P, Zhao G, Jiao K, Chen B, Kan R F, Cao Z H, Liu J G, Ma W G 2022 Front. Phys. 10 857371
Google Scholar
[27] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p180
[28] Gagliardi G, Loock H P 2014 Cavity-Enhanced Spectroscopy and Sensing (Vol. 179) (Berlin: Springer-Verlag) p29
[29] Brown S S, Wilson R W, Ravishankara A R, 2000 J. Phys. Chem. A 104 4976
Google Scholar
[30] Zee R, Hodges J T, Looney J P, 1999 Appl. Opt. 38 3951
Google Scholar
[31] Huang H, Lehmann K K, 2010 Appl. Opt. 49 1378
Google Scholar
[32] Cao Z S, Li Z X, Xu F, Wu Y Q, Zhou Z X, Tong Z M, Ma W G, Zhu W Y 2019 Sensors 19 5232
Google Scholar
[33] Werle P, Mücke R, Slemr F 1993 Appl. Phys. B 57 131
Google Scholar
[34] Gordon I E, Rothman L S, Hill C, et al. 2017 J. Quant. Spectrosc. Radiat. Transfer 203 3
Google Scholar
下载:
计量
- 文章访问数: 4777
- PDF下载量: 121
- 被引次数: 0
