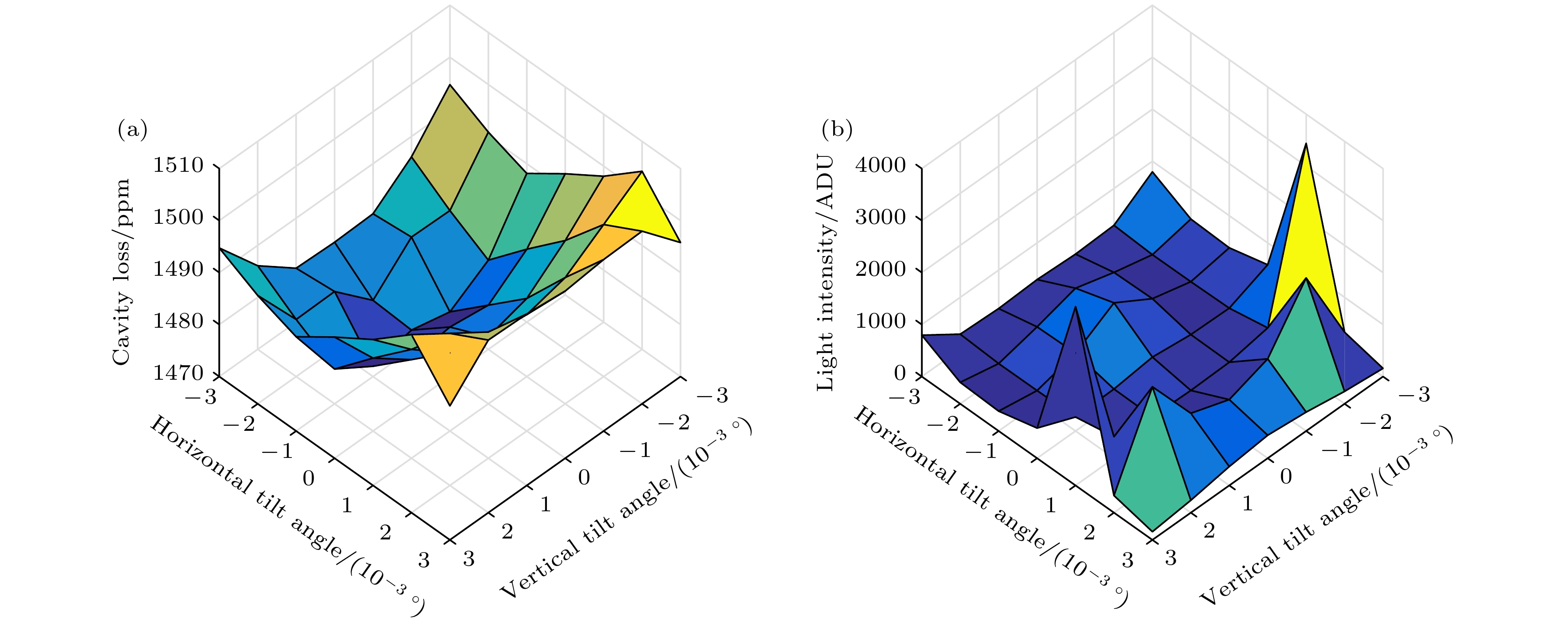
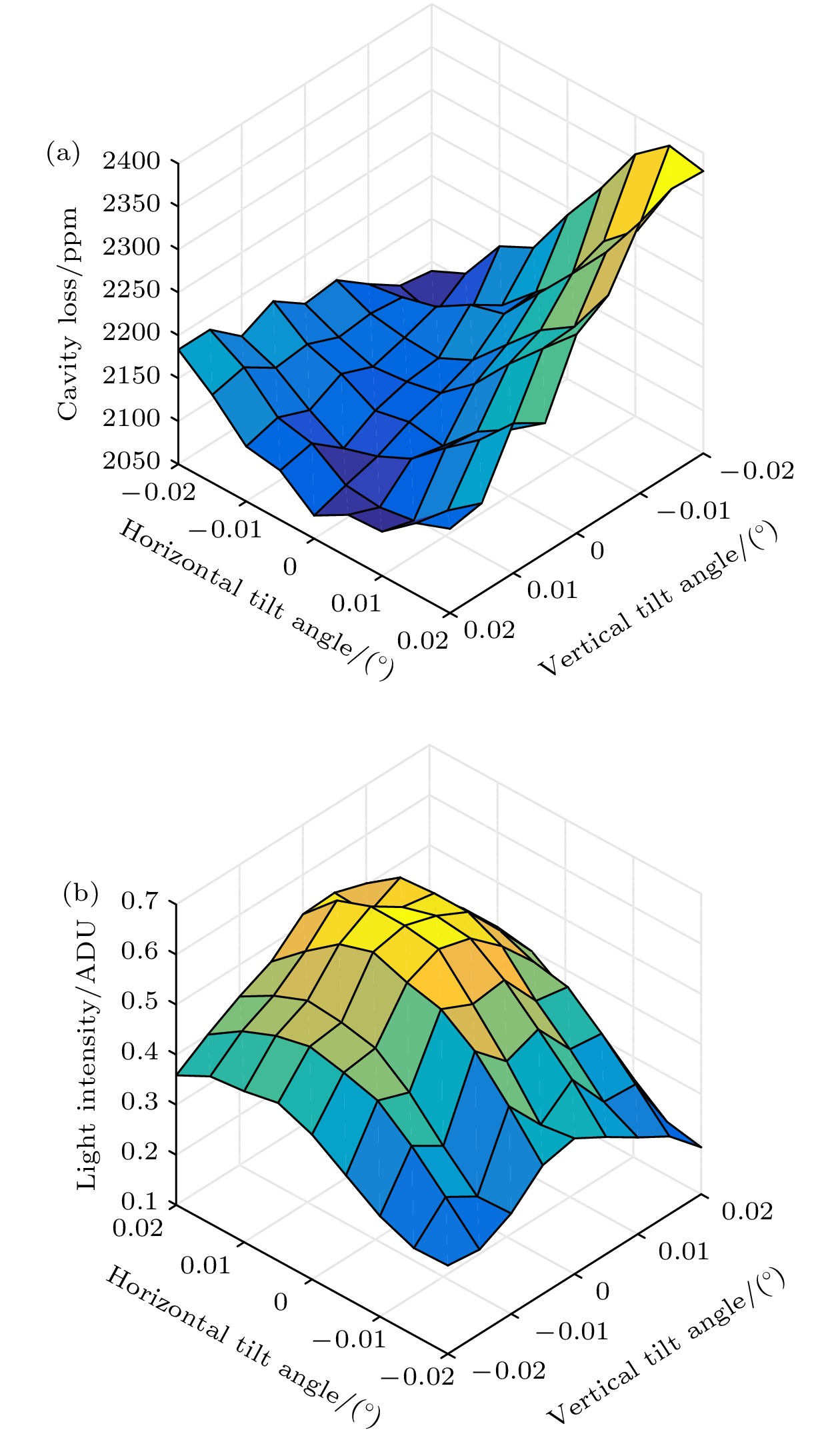
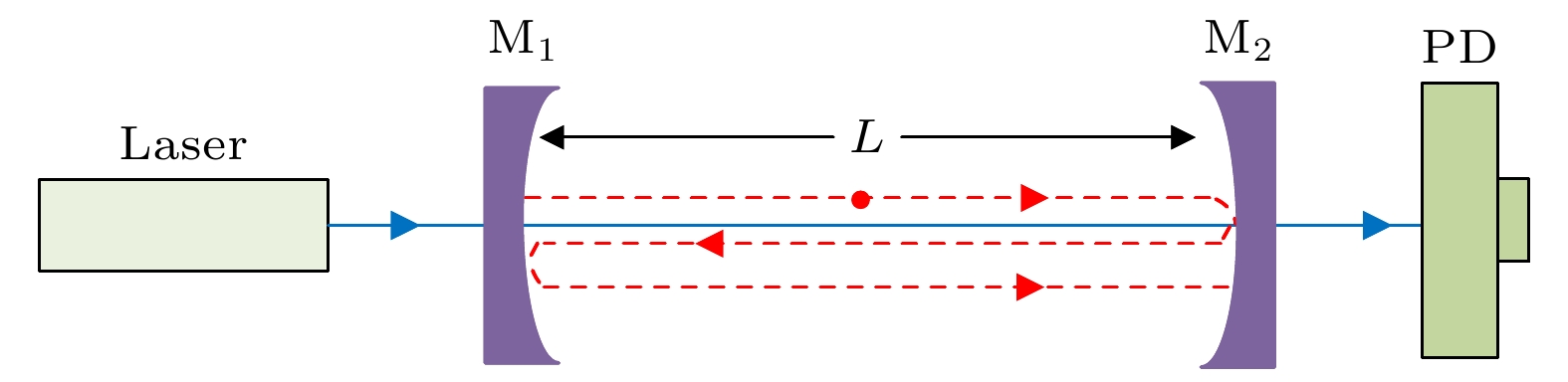
-
在光腔衰荡技术中, 腔失调与腔损耗观测值之间存在复杂的非线性映射关系, 导致调腔过程易陷入局部寻优, 对测量准确性造成影响. 本文基于角谱传播理论, 建立了一种衰荡腔高斯光场传输模型, 对典型调腔评价准则进行对比, 并以模型仿真与实验研究相结合的方式, 验证模型合理性. 在仿真模型和实验系统中对特定腔镜施加二维倾斜角度扫描, 获取两种典型调腔评价准则(即光强峰值和衰荡时间)的二维扫描分布. 对比光强最大峰值和最长衰荡时间所对应的腔损耗观测状态. 仿真结果表明光强最大峰值对应的腔损耗观测误差更小, 观测重复性更高. 实验结果同样表明光强最大峰值评价准则具有更好效果. 模型仿真和实验研究的结果验证光强最大峰值评价准则在仿真和实验中具有更好的调腔重复性精度. 同时, 仿真与实验结果基本吻合, 初步验证了本衰荡腔光场传输模型的合理性. 本光场传输仿真模型对光腔衰荡技术在测量应用、光场响应及自动化调腔技术等方面的研究具有一定参考意义.In cavity ring-down technique, cavity maladjustment has an essential effect on the measurement of intracavity loss. Several adjustment criterions have been adopted to achieve the optimal cavity state. However, experimental study shows that these criterions may correspond to different cavity states, which means that there is discrepancy between different criterions. In view of this problem, a model of intracavity propagation of Gaussian beam is established based on the angular spectrum propagation theory. This model is tested by numerical simulation and experimental research together. In the simulation, the true value of intracavity loss can be known beforehand. The two-dimensional angular scanning is carried out for certain cavity mirror. The two-dimensional distributions of the measure value of intracavity loss and the transmission light intensity are obtained simultaneously. These distributions are both nonlinear and multi-extremum, which will doubtlessly increase the difficulty in realizing the cavity adjustment. By comparing the distributions , we do find the discrepancy between the largest transmission light intensity and the least measured intracavity loss. Meanwhile both of these two states may be not corresponding to the true value in fact. After statistical studies, the relative error of the least measured intracavity loss is (–37.01±11.79) ppm, whereas the relative error of the largest transmission intensity is (–2.70±0.89) ppm. The criterion of the largest transmission intensity shows better stability and repeatability. This model is further tested in a folded cavity ring-down setup. The similar scanning procedure is carried out. A major problem in the experiment is that the true value of intracavity loss cannot be known. So only the repeatability precision of the measured intracavity loss can be analyzed. The statistical results of the largest light intensity and the least measured intracavity loss are ±29.32 ppm and ±70.71 ppm, respectively. The criterion of the largest transmission intensity has better repeatability, which is basically consistent with the simulation result. In this way the rationality of this model can be verified to some degree. In this paper, the criterion of the largest transmission intensity is recommended in the cavity ring-down technique. Furthermore, this model can be a reference for the research of intracavity optical field response, intracavity optical field transmission, unstable resonator alignment, etc.
-
Keywords:
- angular spectrum propagation /
- ring-down cavity /
- intracavity light field transmission /
- cavity maladjustment
[1] Sanders V 1977 Appl. Opt. 16 19
Google Scholar
[2] 李斌成, 龚元 2010 激光与光电子学进展 47 021203
Google Scholar
Li B C, Gong Y 2010 Laser Opt. Pro. 47 021203
Google Scholar
[3] Tan Y, Wang J, Zhao X Q, Liu A W, Hu S M 2017 J. Quant. Spectrosc. Radiat. Transf. 187 274
Google Scholar
[4] 康鹏, 孙羽, 王进, 刘安雯, 胡水明 2018 67 104206
Google Scholar
Kang P, Sun Y, Wang J, Liu A W, Hu S M 2018 Acta Phys. Sin. 67 104206
Google Scholar
[5] McHale L E, Hecobian A, Yalin A P 2016 Opt. Express 24 5523
Google Scholar
[6] Li Z Y, Hu R Z, Xie P H, Chen H, Wu S Y, Wang F Y, Wang Y H, Ling L Y, Liu J G, Liu W Q 2018 Opt. Express 26 A433
Google Scholar
[7] Yang L Z, Yang J J, Yang Y, Zhang Z W, Wang J F, Zhang Z X, Xue P P, Gong Y K, Copner N 2017 Opt. Express 25 2031
Google Scholar
[8] Smith I W 1978 Appl. Opt. 17 2476
Google Scholar
[9] Li B C, Gong Y 2010 US Patent 7 679 750 B2 [2010-03-16]
[10] Cui H, Li B C, Han Y L, Wang J, Gao C M, Wang Y F 2017 Chin. Opt. Lett. 15 053101
Google Scholar
[11] Xiao S L, Li B C, Wang J 2020 Metrologia 57 055002
Google Scholar
[12] Xiang W D, Yang P, Wang S, Xu B, Liu H 2018 Opto-Electronic Advances 1 180024
Google Scholar
[13] Cui H, Li B C, Han Y L, Wang J, Gao C M, Wang Y F 2016 Opt. Express 24 013343
Google Scholar
[14] Hamzeh T, Anam C P, Liu J J 2020 Appl. Opt. 59 9464
Google Scholar
[15] Anderson D Z, Frisch J C, Masser C S 1984 Appl. Opt. 23 1238
Google Scholar
[16] Paldus B A, Kachanov A A 2005 Cana. J. Phys. 83 975
Google Scholar
[17] Romanini D 2014 Appl. Phys. B 115 517
Google Scholar
[18] Shadman S, Rose C, Yalin A P 2016 Appl. Phys. B 122 194
Google Scholar
[19] Maity A, Maithani S, Pradhan M 2021 Anal. Chem. 93 388
Google Scholar
[20] 易亨瑜 2006 中国激光 33 399
Google Scholar
Yi H Y 2006 Chin. J. Lasers 33 399
Google Scholar
[21] 易亨瑜, 吕百达, 张凯 2006 激光技术 30 5
Google Scholar
Yi H Y, Lv B D, Zhang K 2006 Laser Tech. 30 5
Google Scholar
[22] 何星 2016 博士学位论文 (北京: 中国科学院大学)
He X 2016 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[23] He X, Tian Z Z, Lai B H, Zhao W, Wang S, Yang P 2021 CN Patent 113984670A [2022-01-28]
[24] 薛颖, 杜星湖, 何星, 王帅, 杨平, 许冰 2020 中国激光 47 0504001
Google Scholar
Xue Y, Du X H, He X, Wang S, Yang P, Xu B 2020 Chin. J. Lasers 47 0504001
Google Scholar
[25] 杜星湖, 薛颖, 何星, 王帅, 杨平, 许冰 2020 中国激光 47 0604006
Google Scholar
Du X H, Xue Y, He X, Wang S, Yang P, Xu B 2020 Chin. J. Lasers 47 0604006
Google Scholar
[26] Hodges J T, Looney J P, Zee R D V 1996 J. Chem. Phys. 105 10278
Google Scholar
[27] Lehmann K K 1996 J. Chem. Phys. 105 10263
Google Scholar
[28] 吕乃光 2006 傅里叶光学(第二版) (北京: 机械工业出版社) 第82—86页
Lv N G 2006 Fourier Optics (Vol. 2) (Beijing: China Machine Press) pp82–86 (in Chinese)
[29] 曲哲超, 李斌成, 韩艳玲 2011 光子学报 40 1366
Google Scholar
Qu Z C, Li B C, Han Y L 2011 Acta Phot. Sin. 40 1366
Google Scholar
[30] He X, Yan H, Dong L Z, Yang P, Xu B 2016 Chin. Phys. B 25 014211
Google Scholar
[31] He X, Luan Y S, Dong L Z, Yang P, Xu B, Tang G M 2016 Opto-Electronic Engineering 43 46
Google Scholar
-
图 2 (a)腔损耗观测值分布图; (b)透射光强峰值分布图
Fig. 2. (a) Distribution of the cavity loss observation;(b) distribution of the peak value of signal intensity.
图 4 (a)腔损耗观测值分布图; (b)透射光强峰值分布图
Fig. 4. (a) Distribution of the cavity loss observation; (b) distribution of the peak value of signal intensity.
表 1 衰荡腔模型仿真初始参数列表
Table 1. The initial parameters of simulation model
名称 参数 数值 注入
光束横模模式 TEM00 中心波长 λ = 1064 nm 光源线宽* LW = 0.5 nm 束腰半径 w = 0.8 mm 衰荡腔 腔镜反射率 R1 = R2 = 99.85% 腔镜曲率 r1 = r2=1 m 腔长 L = 0.5 m 腔镜偏移量 $ \delta_{x1} =\delta_{71} =\delta_{x2} =\delta_{y2} = 0 $ 传输
过程注入过程 腔内往返传输2000次 衰荡过程 腔内往返传输500次 注: *为在光源线宽范围内, 离散选择30个波长进行仿真. 
下载: 导出CSV
表 2 重复性扫描仿真结果
Table 2. Simulation results of repetitive scanning.
编号 腔镜M1的倾斜失调角度/(°) 光强最大峰值下的腔损耗/ppm 最长衰荡时间下的腔损耗/ppm 腔损耗真值/ppm θx1/(°) θy1/(°) 1 0 0.001 1498.06 1471.98 1500 2 –0.0005 0.001 1497.60 1461.02 1500 3 0.001 0.001 1497.51 1447.07 1500 4 0 0 1496.01 1471.87 1500
下载: 导出CSV
表 3 不同腔镜反射率下的腔损耗仿真结果
Table 3. Simulation results under different cavity mirror reflectivity.
腔镜反射率(R1=R2) 光强最大峰值下的腔损耗测量结果/ppm 最长衰荡时间下的腔损耗测量结果/ppm 99.80% (2000 ppm) 1996.66±0.80 1959.06±13.03 99.85% (1500 ppm) 1497.30±0.89 1462.99±11.79 99.88% (1200 ppm) 1197.63±1.06 1164.80±9.55
下载: 导出CSV
表 4 腔镜M1不同倾斜失调量下的实验结果
Table 4. Experimental results of cavity mirror M1 under different tilt maladjustment.
编号 光强最大峰值下
的腔损耗/ppm最长衰荡时间下
的腔损耗/ppm1 2240.61 2038.26 2 2261.66 2045.96 3 2304.96 1892.29 4 2245.25 1989.59
下载: 导出CSV
-
[1] Sanders V 1977 Appl. Opt. 16 19
Google Scholar
[2] 李斌成, 龚元 2010 激光与光电子学进展 47 021203
Google Scholar
Li B C, Gong Y 2010 Laser Opt. Pro. 47 021203
Google Scholar
[3] Tan Y, Wang J, Zhao X Q, Liu A W, Hu S M 2017 J. Quant. Spectrosc. Radiat. Transf. 187 274
Google Scholar
[4] 康鹏, 孙羽, 王进, 刘安雯, 胡水明 2018 67 104206
Google Scholar
Kang P, Sun Y, Wang J, Liu A W, Hu S M 2018 Acta Phys. Sin. 67 104206
Google Scholar
[5] McHale L E, Hecobian A, Yalin A P 2016 Opt. Express 24 5523
Google Scholar
[6] Li Z Y, Hu R Z, Xie P H, Chen H, Wu S Y, Wang F Y, Wang Y H, Ling L Y, Liu J G, Liu W Q 2018 Opt. Express 26 A433
Google Scholar
[7] Yang L Z, Yang J J, Yang Y, Zhang Z W, Wang J F, Zhang Z X, Xue P P, Gong Y K, Copner N 2017 Opt. Express 25 2031
Google Scholar
[8] Smith I W 1978 Appl. Opt. 17 2476
Google Scholar
[9] Li B C, Gong Y 2010 US Patent 7 679 750 B2 [2010-03-16]
[10] Cui H, Li B C, Han Y L, Wang J, Gao C M, Wang Y F 2017 Chin. Opt. Lett. 15 053101
Google Scholar
[11] Xiao S L, Li B C, Wang J 2020 Metrologia 57 055002
Google Scholar
[12] Xiang W D, Yang P, Wang S, Xu B, Liu H 2018 Opto-Electronic Advances 1 180024
Google Scholar
[13] Cui H, Li B C, Han Y L, Wang J, Gao C M, Wang Y F 2016 Opt. Express 24 013343
Google Scholar
[14] Hamzeh T, Anam C P, Liu J J 2020 Appl. Opt. 59 9464
Google Scholar
[15] Anderson D Z, Frisch J C, Masser C S 1984 Appl. Opt. 23 1238
Google Scholar
[16] Paldus B A, Kachanov A A 2005 Cana. J. Phys. 83 975
Google Scholar
[17] Romanini D 2014 Appl. Phys. B 115 517
Google Scholar
[18] Shadman S, Rose C, Yalin A P 2016 Appl. Phys. B 122 194
Google Scholar
[19] Maity A, Maithani S, Pradhan M 2021 Anal. Chem. 93 388
Google Scholar
[20] 易亨瑜 2006 中国激光 33 399
Google Scholar
Yi H Y 2006 Chin. J. Lasers 33 399
Google Scholar
[21] 易亨瑜, 吕百达, 张凯 2006 激光技术 30 5
Google Scholar
Yi H Y, Lv B D, Zhang K 2006 Laser Tech. 30 5
Google Scholar
[22] 何星 2016 博士学位论文 (北京: 中国科学院大学)
He X 2016 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[23] He X, Tian Z Z, Lai B H, Zhao W, Wang S, Yang P 2021 CN Patent 113984670A [2022-01-28]
[24] 薛颖, 杜星湖, 何星, 王帅, 杨平, 许冰 2020 中国激光 47 0504001
Google Scholar
Xue Y, Du X H, He X, Wang S, Yang P, Xu B 2020 Chin. J. Lasers 47 0504001
Google Scholar
[25] 杜星湖, 薛颖, 何星, 王帅, 杨平, 许冰 2020 中国激光 47 0604006
Google Scholar
Du X H, Xue Y, He X, Wang S, Yang P, Xu B 2020 Chin. J. Lasers 47 0604006
Google Scholar
[26] Hodges J T, Looney J P, Zee R D V 1996 J. Chem. Phys. 105 10278
Google Scholar
[27] Lehmann K K 1996 J. Chem. Phys. 105 10263
Google Scholar
[28] 吕乃光 2006 傅里叶光学(第二版) (北京: 机械工业出版社) 第82—86页
Lv N G 2006 Fourier Optics (Vol. 2) (Beijing: China Machine Press) pp82–86 (in Chinese)
[29] 曲哲超, 李斌成, 韩艳玲 2011 光子学报 40 1366
Google Scholar
Qu Z C, Li B C, Han Y L 2011 Acta Phot. Sin. 40 1366
Google Scholar
[30] He X, Yan H, Dong L Z, Yang P, Xu B 2016 Chin. Phys. B 25 014211
Google Scholar
[31] He X, Luan Y S, Dong L Z, Yang P, Xu B, Tang G M 2016 Opto-Electronic Engineering 43 46
Google Scholar
下载:
计量
- 文章访问数: 3328
- PDF下载量: 62
- 被引次数: 0
