-
冷分子是当下物理学的前沿领域和热点研究方向之一, 早在2004年就有科学家提出将CaH分子作为激光冷却与磁光囚禁的候选分子. 本文首先用三种方法(莫尔斯势法、闭合近似法和RKR反演法)计算CaH分子的弗兰克-康登因子, 证实了CaH的
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ 态和$ {\mathrm{A}}^{2}\Pi _{1/2} $ 态之间具有高度对角化的弗兰克-康登因子矩阵. 随后, 采用有效哈密顿量的方法研究了基态$ {\mathrm{X}}^{2}\Sigma _{1/2} $ 的超精细能级结构和$ {\mathrm{A}}^{2}\Pi _{1/2}\left(J=1/2, \mathrm{ }+\right)\leftarrow {\mathrm{X}}^{2}\Sigma _{1/2}\left(N=1, \mathrm{ }-\right) $ 跃迁的超精细跃迁分支比, 并提出可同时覆盖超精细能级的边带调制方案. 最后, 为探究CaH分子磁光囚禁的相关性质, 计算了$ |X, \mathrm{ }N=1, -\rangle $ 态的塞曼效应和 J 混合下的朗德 g 因子. 以上工作不仅证明了激光冷却和磁光囚禁CaH分子的可行性, 而且对天体物理学中的光谱分析、超冷分子碰撞以及探索基本对称性破缺等基础物理学的相关研究也具有一定的参考意义.Laser cooling and trapping of neutral molecules has made substantial progress in the past few years. On one hand, molecules have more complex energy level structures than atoms, thus bringing great challenges to direct laser cooling and trapping; on the other hand, cold molecules show great advantages in cold molecular collisions and cold chemistry, as well as the applications in many-body interactions and fundamental physics such as searching for fundamental symmetry violations. In recent years, polar diatomic molecules such as SrF, YO, and CaF have been demonstrated experimentally in direct laser cooling techniques and magneto-optic traps (MOTs), all of which require a comprehensive understanding of their molecular internal level structures. Other suitable candidates have also been proposed, such as YbF, MgF, BaF, HgF or even SrOH and YbOH, some of which are already found to play important roles in searching for variations of fundamental constants and the measurement of the electron’s Electric Dipole Moment (eEDM). As early as 2004, the CaH molecule was selected as a good candidate for laser cooling and magneto-optical trapping. In this article, we first theoretically investigate the Franck−Condon factors of CaH in the${{\rm{A}}}^{2}\Pi _{1/2}\leftarrow {{\rm{X}}}^{2}\Sigma _{1/2}$ transition by the Morse potential method, the closed-form approximation method and the Rydberg-Klein-Rees method separately, and prove that Franck−Condon factor matrix between$ {\mathrm{X}}^{2}\Sigma _{1/2} $ state and$ {\mathrm{A}}^{2}\Pi _{1/2} $ state is highly diagonalized, and indicate that sum of f00, f01 and f02 for each molecule is greater than 0.9999 and almost 1 × 104 photons can be scattered to slow the molecules with merely three lasers. The molecular hyperfine structures of$ {X}^{2}\Sigma _{1/2} $ , as well as the transitions and associated hyperfine branching ratios in the${{\rm{A}}}^{2}\Pi _{1/2}\left(J=1/2, \mathrm{ }+\right)\leftarrow {{\rm{X}}}^{2}\Sigma _{1/2}\left(N=1, \mathrm{ }-\right)$ transition of CaH, are examined via the effective Hamiltonian approach. According to these results, in order to fully cover the hyperfine manifold originating from$ |X, \mathrm{ }N=1, -\rangle $ , we propose the sideband modulation scheme that at least two electro-optic modulators (EOMs) should be required for CaH when detuning within 3Γ of the respective hyperfine transition. In the end, we analyze the Zeeman structures and magnetic g factors with and without J mixing of the$ |X, \mathrm{ }N=1, -\rangle $ state to undercover more information about the magneto-optical trapping. Our work here not only demonstrates the feasibility of laser cooling and trapping of CaH, but also illuminates the studies related to spectral analysis in astrophysics, ultracold molecular collisions and fundamental physics such as exploring the fundamental symmetry violations.-
Keywords:
- cold molecules /
- laser cooling /
- CaH molecule /
- Franck-Condon factors
[1] Schioppo M, Brown R C, McGrew W F, Hinkley N, Fasano R J, Beloy K, Yoon T H, Milani G, Nicolodi D, Sherman J A, Phillips N B, Oates C W, Ludlow A D 2016 Nat. Photonics 11 48
[2] Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201
Google Scholar
[3] Nicholson T L, Campbell S L, Hutson R B, Marti G E, Bloom B J, McNally R L, Zhang W, Barrett M D, Safronova M S, Strouse G F, Tew W L, Ye J 2015 Nat. Commun. 6 6896
Google Scholar
[4] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[5] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[6] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198
Google Scholar
[7] Hadzibabic Z, Krüger P, Cheneau M, Battelier B, Dalibard J 2006 Nature 441 1118
Google Scholar
[8] Müller H, Peters A, Chu S 2010 Nature 463 926
Google Scholar
[9] Huntemann N, Lipphardt B, Tamm C, Gerginov V, Weyers S, Peik E 2014 Phys. Rev. Lett. 113 210802
Google Scholar
[10] Bouchendira R, Cladé P, Guellati-Khélifa S, Nez F, Biraben F 2011 Phys. Rev. Lett. 106 080801
Google Scholar
[11] Parker R H, Yu C, Zhong W, Estey B, Müller H 2018 Science 360 191
Google Scholar
[12] Godun R M, Nisbet-Jones P B R, Jones J M, King S A, Johnson L A M, Margolis H S, Szymaniec K, Lea S N, Bongs K, Gill P 2014 Phys. Rev. Lett. 113 210801
Google Scholar
[13] Jaffe M, Haslinger P, Xu V, Hamilton P, Upadhye A, Elder B, Khoury J, Müller H 2017 Nat. Phys. 13 938
Google Scholar
[14] Asenbaum P, Overstreet C, Kovachy T, Brown D D, Hogan J M, Kasevich M A 2017 Phys. Rev. Lett. 118 183602
Google Scholar
[15] Omran A, Levine H, Keesling A, Semeghini G, Wang T T, Ebadi S, Bernien H, Zibrov A S, Pichler H, Choi S, Cui J, Rossignolo M, Rembold P, Montangero S, Calarco T, Endres M, Greiner M, Vuletić V, Lukin M D 2019 Science 365 570
Google Scholar
[16] Friis N, Marty O, Maier C, Hempel C, Holzäpfel M, Jurcevic P, Plenio M B, Huber M, Roos C, Blatt R, Lanyon B 2018 Phys. Rev. X 8 021012
[17] Chin C, Flambaum V V, Kozlov M G 2009 New J. Phys. 11
[18] DeMille D, Cahn S B, Murphree D, Rahmlow D A, Kozlov M G 2008 Phys. Rev. Lett. 100 023003
Google Scholar
[19] Baron J, Campbell W C, DeMille D, Doyle J M, Gabrielse G, Gurevich Y V, Hess P W, Hutzler N R, Kirilov E, Kozyryev I, O’Leary B R, Panda C D, Parsons M F, Petrik E S, Spaun B, Vutha A C, West A D 2014 Science 343 269
Google Scholar
[20] Hudson J J, Sauer B E, Tarbutt M R, Hinds E A 2002 Phys. Rev. Lett. 89 023003
Google Scholar
[21] Bohn J L, Rey A M, Ye J 2017 Science 357 1002
Google Scholar
[22] Baranov M A, Dalmonte M, Pupillo G, Zoller P 2012 Chem. Rev. 112 5012
Google Scholar
[23] Kotochigova S, Zelevinsky T, Ye J 2009 Phys. Rev. A 79 012504
Google Scholar
[24] Murphy T M, Flambaum V V, Muller S, Henkel C 2008 Science 320 1611
Google Scholar
[25] Zelevinsky T, Kotochigova S, Ye J 2008 Phys. Rev. Lett. 100 043201
Google Scholar
[26] Cairncross W B, Gresh D N, Grau M, Cossel K C, Roussy T S, Ni Y, Zhou Y, Ye J, Cornell E A 2017 Phys. Rev. Lett. 119 153001
Google Scholar
[27] Di Rosa M D 2004 Eur. Phys. J. D 31 395
Google Scholar
[28] Shuman E S, Barry J F, Glenn D R, DeMille D 2009 Phys. Rev. Lett. 103 1
[29] Shuman E S, Barry J F, DeMille D 2010 Nature 467 820
Google Scholar
[30] Barry J F, Shuman E S, Norrgard E B, DeMille D 2012 Phys. Rev. Lett. 108 103002
Google Scholar
[31] Hummon M T, Yeo M, Stuhl B K, Collopy A L, Xia Y, Ye J 2013 Phys. Rev. Lett. 110 143001
Google Scholar
[32] Zhelyazkova V, Cournol A, Wall T E, Matsushima A, Hudson J J, Hinds E A, Tarbutt M R, Sauer B E 2014 Phys. Rev. A 89 053416
Google Scholar
[33] Hemmerling B, Chae E, Ravi A, Anderegg L, Drayna G K, Hutzler N R, Collopy A L, Ye J, Ketterle W, Doyle J M 2016 J. Phys. B 49 174001
Google Scholar
[34] Truppe S, Williams H J, Fitch N J, Hambach M, Wall T E, Hinds E A 2017 New J. Phys. 19 1
[35] Iwata G Z, McNally R L, Zelevinsky T 2017 Phys. Rev. A 96 022509
Google Scholar
[36] Bu W, Chen T, Lv G, Yan B 2017 Phys. Rev. A 95 1
[37] Lim J, Almond J R, Trigatzis M A, Devlin J A, Fitch N J, Sauer B E, Tarbutt R M, Hinds E A 2018 Phys. Rev. Lett. 120 123201
Google Scholar
[38] Kozyryev I, Baum L, Matsuda K, Augenbraun B L, Anderegg L, Sedlack A P, Doyle J M 2017 Phys. Rev. Lett. 118 173201
Google Scholar
[39] Burgasser A J, Kirkpatrick J D, Liebert J, Burrows A 2003 Astrophys. J. 594 510
Google Scholar
[40] Yadin B, Veness T, Conti P, Hill C, Yurchenko S N, Tennyson J 2012 Mon. Not. R. Astron. Soc. 425 34
Google Scholar
[41] Sotirowski P 1972 Astron. Astrophys. Suppl. Ser. 6 85
[42] Woolf V M, Wallerstein G, Month N R 2004 Astron. Soc. 350 1365
[43] Shkolnik E, Liu M C, Reid I N 2009 Astrophys. J. 699 649
Google Scholar
[44] Habli H, Jellali S, Oujia B 2020 Phys. Scr. 95 015403
Google Scholar
[45] Fazil N M, Prasannaa V S, Latha K V P, Abe M, Das B P 2018 Phys. Rev. A 98 032511
Google Scholar
[46] Shayesteh A, Ram R S, Bernath P F 2013 J. Mol. Spectrosc. 288 46
Google Scholar
[47] GharibNezhad E, Shayesteh A, Bernath P F 2012 J. Mol. Spectrosc. 281 47
Google Scholar
[48] Li G, Harrison J J, Ram R S, Western C M, Bernath P F 2012 J Quant. Spectrosc. Radiat. Transfer 113 67
Google Scholar
[49] Liu M, Pauchard T, Sjödin M, Launila O, van der Meulen P, Berg L E 2009 J. Mol. Spectrosc. 257 105
Google Scholar
[50] Gao Y, Gao T 2014 Phys. Rev. A 90 052506
Google Scholar
[51] Nicholls R W 1981 J. Suppl. Ser. 47 279
Google Scholar
[52] Frank A, Rivera A L, Wolf K B 2000 Phys. Rev. A 61 054102
Google Scholar
[53] Rees A L G 1947 Proc. Phys. Soc. 59 998
Google Scholar
[54] Roy R J L 2007 LEVEL8.0: A Compute Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels (Waterloo: University of Waterloo) No. CP-663 [Chemical Physics Research Report]
[55] Berg L E, Klynning L 1974 Phys. Scr. 10 331
Google Scholar
[56] Knight L B, Weltner W 1971 J. Chem. Phys. 54 3875
Google Scholar
[57] Frosch R A, Foley H M 1952 Phys. Rev. 88 1337
Google Scholar
[58] Zare R N 1988 Angular Momentum (New York: A Wiley-Interscience Publication) pp186–191
[59] Barclay W L, J r., Anderson M A, Ziurys L M 1993 Astrophys. J. 408 L65
Google Scholar
[60] Sauer B E, Wang J, Hinds E A 1996 J. Chem. Phys. 105 7412
Google Scholar
[61] Brown J H, Carrington A 2012 Rotational Spectroscopy of Diatomic Molecules (Cambridge: Cambridge University Press) pp230–251
[62] Chen T, Bu W, Yan B 2016 Phys. Rev. A 94 063415
Google Scholar
[63] Xu L, Yin Y N, Wei B, Xia Y, Yin J P 2016 Phys. Rev. A 93 013408
Google Scholar
-
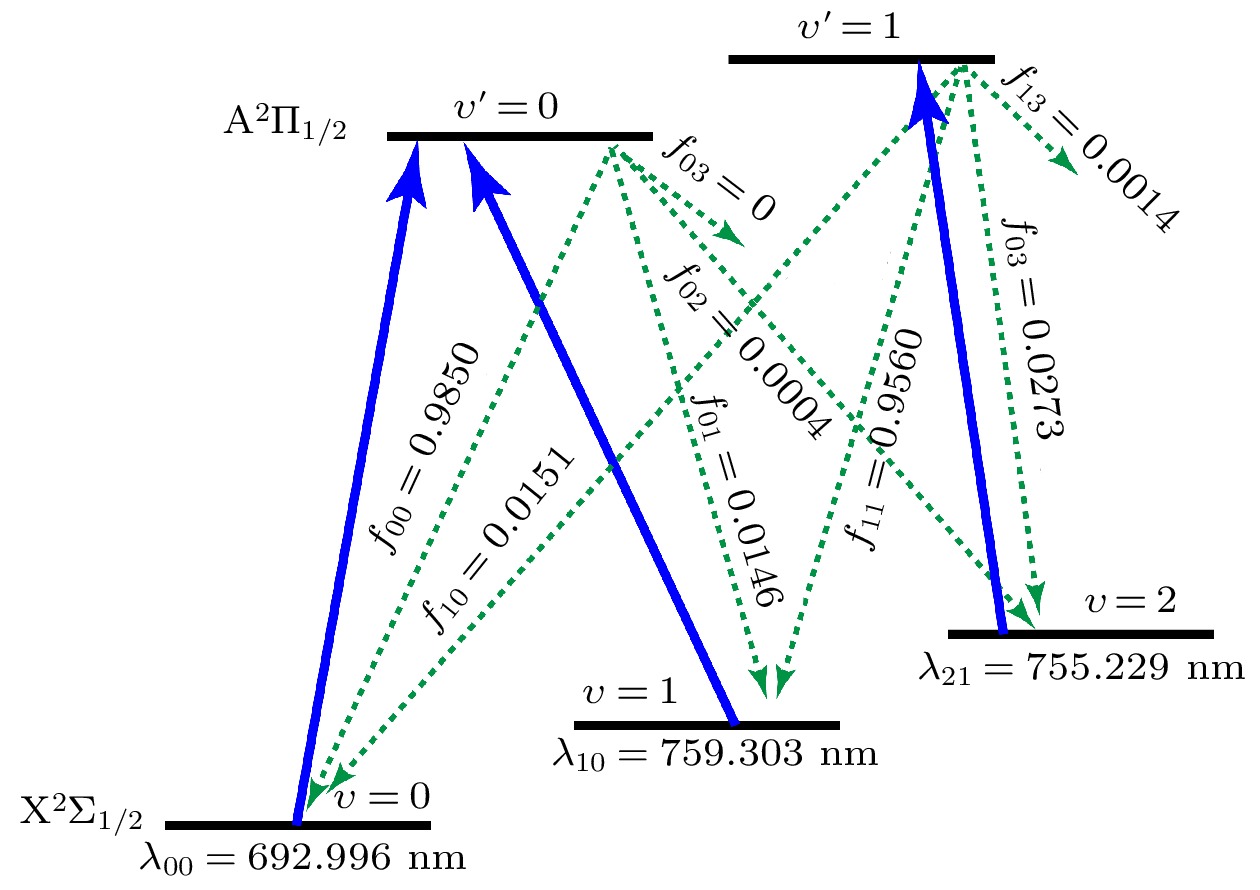
图 2 CaH分子准封闭跃迁循环的激光冷却方案. 其中的蓝线表示泵浦激光,
$ {\lambda }_{\upsilon {\upsilon }'} $ 表示泵浦激光的跃迁波长, 绿色虚线表示从$ {\mathrm{A}}^{2}\Pi _{1/2} $ 态自发辐射的衰变率, 即F-C因子$ {f}_{{\upsilon }'\upsilon } $ Fig. 2. Proposed scheme to create a quasi-closed cycling transition for laser cooling of CaH. Blue solid lines indicate the laser-driven transitions at the wavelengths
$ {\lambda }_{\upsilon {\upsilon }'} $ , while green dotted lines indicate the spontaneous decays from the$ {\mathrm{A}}^{2}\Pi _{1/2} $ state along with the corresponding F-C factors$ {f}_{{\upsilon }'\upsilon } $ .
图 3 CaH转动能级和超精细能级的能级分裂以及准封闭的跃迁循环. 根据选择定则, 由
$|A, {\upsilon }'=0, {J}'=1/2, +\rangle \leftarrow$ $ |X, \upsilon =0, N=1, \mathrm{ }-\rangle $ 跃迁(绿色实线)被泵浦到上能级的分子将会自发辐射回N = 1的基态Fig. 3. Energy splitting between different rotational hyperfine levels and the closure of the rotational structures for CaH. Due to selection rules, driving the
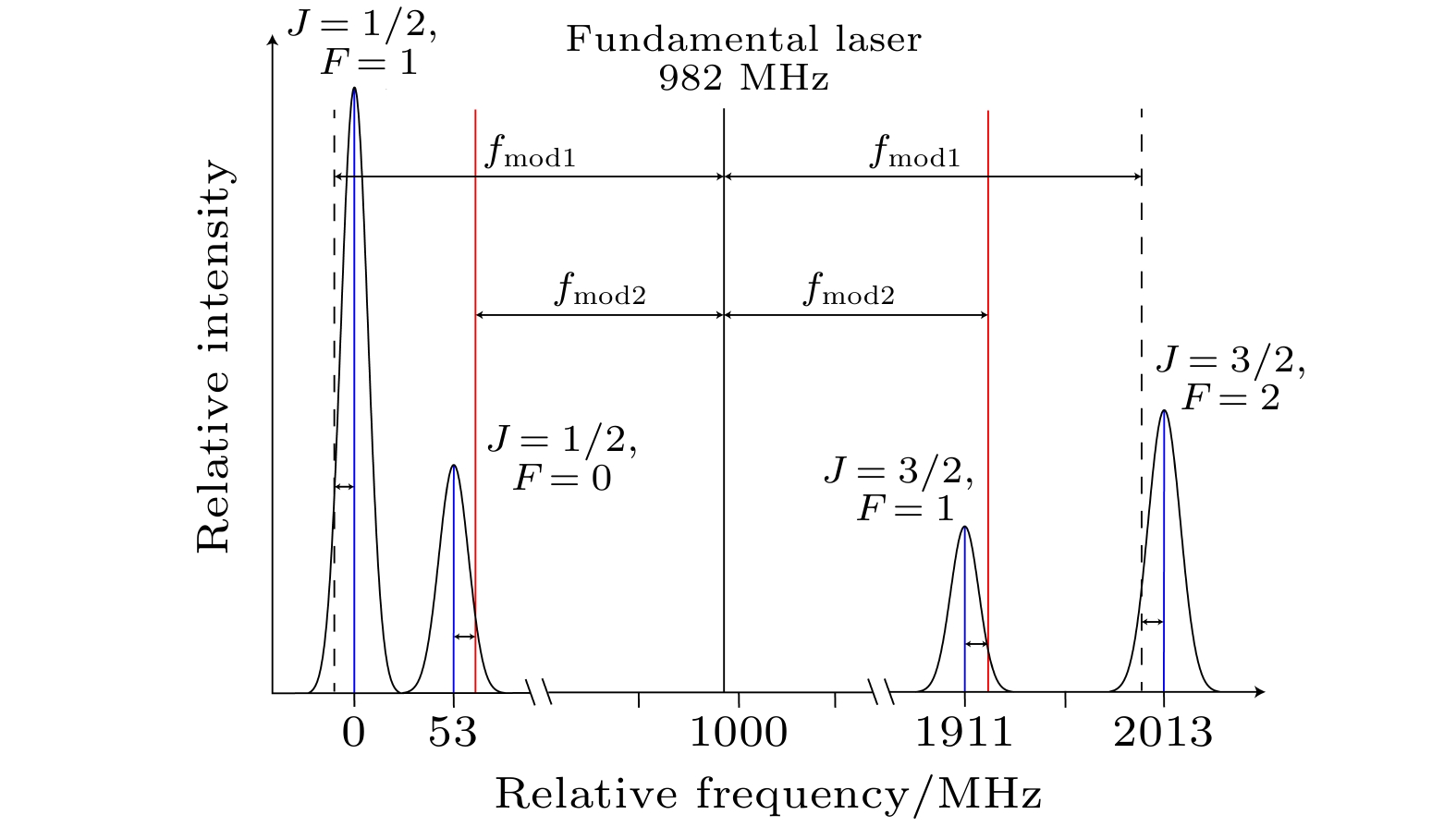
$|A, {\upsilon }'=0, {J}'= $ $ 1/2, +\rangle \leftarrow |X, \upsilon =0, N=1, \mathrm{ }-\rangle$ transition (green solid upward lines) will allow a spontaneous decay (green dotted downward line) that goes back to N = 1 state.
图 4 能同时覆盖CaH分子
$ |X, \mathrm{ }N=1, -\rangle $ 态下四个子能级的边带调制方案. 中间的黑色实线表示基频光; 蓝色实线表示超精细能级的中心频率; 黑色虚线与红色实线分别表示两个EOM的边带, 调制频率分别为fmod1 = 994.25 MHz 和 fmod2 = 941.25 MHz. 每个边带的失谐量均控制在3Γ内Fig. 4. Proposed sideband modulation scheme to simultaneously cover all hyperfine transitions originating from the
$ |X, \mathrm{ }N=1, -\rangle $ state of CaH. The black solid line in the middle indicates the fundamental laser frequency, while the blue solid line corresponds to the central frequency of the hyperfine transitions. The black dash line and the red solid line represent the sidebands of two EOMs respectively with the modulating frequencies fmod1 = 994.25 MHz and fmod2 = 941.25 MHz. All the hyperfine levels are well addressed for detuning within 3Γ of the respective hyperfine transition.
图 5 CaH在
$ |X, \mathrm{ }N=1, -\rangle $ 态的塞曼能移. 红线和蓝线分别表示$ \left|J=3/2, \right.F=2\rangle $ 态和$ \left|J=3/2, \right.F=1\rangle $ 态, 黑线代表了$ \left|J=1/2, \right.F=0\rangle $ 态和$ \left|J=1/2, \right.F=1\rangle $ 态Fig. 5. Zeeman structures for the
$ |X, \mathrm{ }N=1, -\rangle $ state of CaH. The red and blue lines indicate the energy levels for$ \left|J=3/2, \right.F=2\rangle $ and$ \left|J=3/2, \right.F=1\rangle $ states, while the black lines represent the energy levels for$ \left|J=1/2, \right.F=0\rangle $ and$ \left|J=1/2, \right.F=1\rangle $ states, respectively.表 2 用三种方法(闭合近似法、莫尔斯势法和RKR反演法)计算的CaH分子的部分F-C因子
Table 2. Calculated Franck-Condon factors of CaH by the closed-form approximation method, the Morse potential method and the RKR inversion method.
方法 f00 f01 f02 f11 f13 闭合近似 0.9846 0.0152 0.0001 0.9545 0.00035 莫尔斯势 0.9850 0.0146 0.0004 0.9560 0.0014 RKR反演 0.99542 0.00454 0.00004 0.98631 0.00012 Ref. [50] 0.961 0.038 0.002 0.885 0.005 
下载: 导出CSV
表 3 CaH分子
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ 态和$ {\mathrm{A}}^{2}\Pi _{1/2} $ 间跃迁波长的计算值和实验值, 括号内的数值代表最后位的不确定度(标准偏差)Table 3. Comparison between the calculated and experimental results of the transition wavelengths between
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ and$ {\mathrm{A}}^{2}\Pi _{1/2} $ states of CaH. Numbers in parentheses indicate the uncertainty (standard deviation) in the last figures.
下载: 导出CSV
表 4 CaH分子
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ 态的转动常数和超精细结构常数Table 4. Rotational and hyperfine structure parameters for the
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ state of CaH.参数 Ref. [59] $ {B}_{\upsilon } $/MHz 126772.935 $ {D}_{\upsilon } $/MHz 5.546 $ {\gamma_\upsilon } $/MHz 1305.755 $ {b}_{\upsilon } $/MHz 155.785 $ {c}_{\upsilon } $/MHz 4.74
下载: 导出CSV
表 5 CaH分子
$ {\mathrm{A}}^{2}\Pi _{1/2}\leftarrow {\mathrm{X}}^{2}\Sigma _{1/2} $ 的超精细跃迁频率(ΔJ = 0和1, ΔF = ± 1和0).Table 5. Calculated frequencies for hyperfine transitions
$ {\mathrm{A}}^{2}\Pi _{1/2}\leftarrow {\mathrm{X}}^{2}\Sigma _{1/2} $ (ΔJ = 0 and 1, ΔF = ± 1 and 0) for CaH.$ N\to N' $ $J \to J'$ $F \to F' $ νcal/MHz νexpa/MHz νcal– νexp/MHz 0$ \to $1 1/2$ \to $1/2 1$ \to $1 252163.0907 252163.082 0.0087 1$ \to $0 252216.3510 252216.347 0.004 0$ \to $1 252320.4557 252320.467 –0.0113 1/2$ \to $3/2 1$ \to $1 254074.8288 254074.834 –0.0052 1$ \to $2 254176.4055 254176.415 –0.0095 0$ \to $1 254232.1938 254232.179 0.0148 aRef. [59]
下载: 导出CSV
表 6 CaH分子
$ |X, \upsilon =0, \mathrm{ }N=1, \mathrm{ }-\rangle $ 态理想的组分和考虑J混合的组分Table 6. Nominal labels and actual labels due to J mixing for the
$ |X, N=1, -\rangle $ state of CaH molecules.理想的组分 考虑 J 混合后真实的组分 $ \left|J=3/2, \right.F=2\rangle $ $ \left|J=3/2, \right.F=2\rangle $ $ \left|J=3/2, \right.F=1\rangle $ $0.999238\left|J=3/2, \right.F=1\rangle +\\0.039028\left|J=1/2, \right.F=1\rangle$ $ \left|J=1/2, \right.F=1\rangle $ $-0.039028\left|J=3/2, \right.F=1\rangle +\\0.999238\left|J=1/2, \right.F=1\rangle$ $ \left|J=1/2, \right.F=0\rangle $ $ \left|J=1/2, \right.F=0\rangle $
下载: 导出CSV
表 7 CaH分子
$ |A, \mathrm{ }J'=1/2, +\rangle $ 态跃迁到$|X, \mathrm{ }N= $ $ 1, -\rangle$ 态的超精细跃迁分支比Table 7. Calculated hyperfine branching ratios for decays from
$ |A, \mathrm{ }J'=1/2, +\rangle $ to$ |X, \mathrm{ }N=1, -\rangle $ for CaH molecules.J F MF F' = 0 F' = 1 $M'_{\rm F} = 0$ $M'_{\rm F} = -1$ $M'_{\rm F} = 0$ $M'_{\rm F} = 1$ 3/2 –2 0.000000 0.166667 0.000000 0.000000 –1 0.000000 0.083333 0.083333 0.000000 0 0.000000 0.027778 0.111111 0.027778 1 0.000000 0.000000 0.083333 0.083333 2 0.000000 0.000000 0.000000 0.166667 3/2 –1 0.099024 0.034202 0.034202 0.000000 0 0.099024 0.034202 0.000000 0.034202 1 0.099024 0.000000 0.034202 0.034202 1/2 –1 0.234309 0.215798 0.215798 0.000000 0 0.234309 0.215798 0.000000 0.215798 1 0.234309 0.000000 0.215798 0.215798 1/2 0 0.000000 0.222222 0.222222 0.222222
下载: 导出CSV
表 8 CaH分子
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ ($ \upsilon =0, N=1 $ )态的朗德g因子Table 8. The g factors for the
$ {\mathrm{X}}^{2}\Sigma _{1/2} $ ($\upsilon =0, $ $ N=1$ ) state of CaH molecules.态 g (没有J 混合) g (有J 混合) $ \left|J=3/2, \right.F=2\rangle $ 0.50 0.50 $ \left|J=3/2, \right.F=1\rangle $ 0.83 0.865 $ \left|J=1/2, \right.F=1\rangle $ –0.33 –0.365 $ \left|J=1/2, \right.F=0\rangle $ 0.00 0.000
下载: 导出CSV
-
[1] Schioppo M, Brown R C, McGrew W F, Hinkley N, Fasano R J, Beloy K, Yoon T H, Milani G, Nicolodi D, Sherman J A, Phillips N B, Oates C W, Ludlow A D 2016 Nat. Photonics 11 48
[2] Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201
Google Scholar
[3] Nicholson T L, Campbell S L, Hutson R B, Marti G E, Bloom B J, McNally R L, Zhang W, Barrett M D, Safronova M S, Strouse G F, Tew W L, Ye J 2015 Nat. Commun. 6 6896
Google Scholar
[4] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[5] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[6] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198
Google Scholar
[7] Hadzibabic Z, Krüger P, Cheneau M, Battelier B, Dalibard J 2006 Nature 441 1118
Google Scholar
[8] Müller H, Peters A, Chu S 2010 Nature 463 926
Google Scholar
[9] Huntemann N, Lipphardt B, Tamm C, Gerginov V, Weyers S, Peik E 2014 Phys. Rev. Lett. 113 210802
Google Scholar
[10] Bouchendira R, Cladé P, Guellati-Khélifa S, Nez F, Biraben F 2011 Phys. Rev. Lett. 106 080801
Google Scholar
[11] Parker R H, Yu C, Zhong W, Estey B, Müller H 2018 Science 360 191
Google Scholar
[12] Godun R M, Nisbet-Jones P B R, Jones J M, King S A, Johnson L A M, Margolis H S, Szymaniec K, Lea S N, Bongs K, Gill P 2014 Phys. Rev. Lett. 113 210801
Google Scholar
[13] Jaffe M, Haslinger P, Xu V, Hamilton P, Upadhye A, Elder B, Khoury J, Müller H 2017 Nat. Phys. 13 938
Google Scholar
[14] Asenbaum P, Overstreet C, Kovachy T, Brown D D, Hogan J M, Kasevich M A 2017 Phys. Rev. Lett. 118 183602
Google Scholar
[15] Omran A, Levine H, Keesling A, Semeghini G, Wang T T, Ebadi S, Bernien H, Zibrov A S, Pichler H, Choi S, Cui J, Rossignolo M, Rembold P, Montangero S, Calarco T, Endres M, Greiner M, Vuletić V, Lukin M D 2019 Science 365 570
Google Scholar
[16] Friis N, Marty O, Maier C, Hempel C, Holzäpfel M, Jurcevic P, Plenio M B, Huber M, Roos C, Blatt R, Lanyon B 2018 Phys. Rev. X 8 021012
[17] Chin C, Flambaum V V, Kozlov M G 2009 New J. Phys. 11
[18] DeMille D, Cahn S B, Murphree D, Rahmlow D A, Kozlov M G 2008 Phys. Rev. Lett. 100 023003
Google Scholar
[19] Baron J, Campbell W C, DeMille D, Doyle J M, Gabrielse G, Gurevich Y V, Hess P W, Hutzler N R, Kirilov E, Kozyryev I, O’Leary B R, Panda C D, Parsons M F, Petrik E S, Spaun B, Vutha A C, West A D 2014 Science 343 269
Google Scholar
[20] Hudson J J, Sauer B E, Tarbutt M R, Hinds E A 2002 Phys. Rev. Lett. 89 023003
Google Scholar
[21] Bohn J L, Rey A M, Ye J 2017 Science 357 1002
Google Scholar
[22] Baranov M A, Dalmonte M, Pupillo G, Zoller P 2012 Chem. Rev. 112 5012
Google Scholar
[23] Kotochigova S, Zelevinsky T, Ye J 2009 Phys. Rev. A 79 012504
Google Scholar
[24] Murphy T M, Flambaum V V, Muller S, Henkel C 2008 Science 320 1611
Google Scholar
[25] Zelevinsky T, Kotochigova S, Ye J 2008 Phys. Rev. Lett. 100 043201
Google Scholar
[26] Cairncross W B, Gresh D N, Grau M, Cossel K C, Roussy T S, Ni Y, Zhou Y, Ye J, Cornell E A 2017 Phys. Rev. Lett. 119 153001
Google Scholar
[27] Di Rosa M D 2004 Eur. Phys. J. D 31 395
Google Scholar
[28] Shuman E S, Barry J F, Glenn D R, DeMille D 2009 Phys. Rev. Lett. 103 1
[29] Shuman E S, Barry J F, DeMille D 2010 Nature 467 820
Google Scholar
[30] Barry J F, Shuman E S, Norrgard E B, DeMille D 2012 Phys. Rev. Lett. 108 103002
Google Scholar
[31] Hummon M T, Yeo M, Stuhl B K, Collopy A L, Xia Y, Ye J 2013 Phys. Rev. Lett. 110 143001
Google Scholar
[32] Zhelyazkova V, Cournol A, Wall T E, Matsushima A, Hudson J J, Hinds E A, Tarbutt M R, Sauer B E 2014 Phys. Rev. A 89 053416
Google Scholar
[33] Hemmerling B, Chae E, Ravi A, Anderegg L, Drayna G K, Hutzler N R, Collopy A L, Ye J, Ketterle W, Doyle J M 2016 J. Phys. B 49 174001
Google Scholar
[34] Truppe S, Williams H J, Fitch N J, Hambach M, Wall T E, Hinds E A 2017 New J. Phys. 19 1
[35] Iwata G Z, McNally R L, Zelevinsky T 2017 Phys. Rev. A 96 022509
Google Scholar
[36] Bu W, Chen T, Lv G, Yan B 2017 Phys. Rev. A 95 1
[37] Lim J, Almond J R, Trigatzis M A, Devlin J A, Fitch N J, Sauer B E, Tarbutt R M, Hinds E A 2018 Phys. Rev. Lett. 120 123201
Google Scholar
[38] Kozyryev I, Baum L, Matsuda K, Augenbraun B L, Anderegg L, Sedlack A P, Doyle J M 2017 Phys. Rev. Lett. 118 173201
Google Scholar
[39] Burgasser A J, Kirkpatrick J D, Liebert J, Burrows A 2003 Astrophys. J. 594 510
Google Scholar
[40] Yadin B, Veness T, Conti P, Hill C, Yurchenko S N, Tennyson J 2012 Mon. Not. R. Astron. Soc. 425 34
Google Scholar
[41] Sotirowski P 1972 Astron. Astrophys. Suppl. Ser. 6 85
[42] Woolf V M, Wallerstein G, Month N R 2004 Astron. Soc. 350 1365
[43] Shkolnik E, Liu M C, Reid I N 2009 Astrophys. J. 699 649
Google Scholar
[44] Habli H, Jellali S, Oujia B 2020 Phys. Scr. 95 015403
Google Scholar
[45] Fazil N M, Prasannaa V S, Latha K V P, Abe M, Das B P 2018 Phys. Rev. A 98 032511
Google Scholar
[46] Shayesteh A, Ram R S, Bernath P F 2013 J. Mol. Spectrosc. 288 46
Google Scholar
[47] GharibNezhad E, Shayesteh A, Bernath P F 2012 J. Mol. Spectrosc. 281 47
Google Scholar
[48] Li G, Harrison J J, Ram R S, Western C M, Bernath P F 2012 J Quant. Spectrosc. Radiat. Transfer 113 67
Google Scholar
[49] Liu M, Pauchard T, Sjödin M, Launila O, van der Meulen P, Berg L E 2009 J. Mol. Spectrosc. 257 105
Google Scholar
[50] Gao Y, Gao T 2014 Phys. Rev. A 90 052506
Google Scholar
[51] Nicholls R W 1981 J. Suppl. Ser. 47 279
Google Scholar
[52] Frank A, Rivera A L, Wolf K B 2000 Phys. Rev. A 61 054102
Google Scholar
[53] Rees A L G 1947 Proc. Phys. Soc. 59 998
Google Scholar
[54] Roy R J L 2007 LEVEL8.0: A Compute Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels (Waterloo: University of Waterloo) No. CP-663 [Chemical Physics Research Report]
[55] Berg L E, Klynning L 1974 Phys. Scr. 10 331
Google Scholar
[56] Knight L B, Weltner W 1971 J. Chem. Phys. 54 3875
Google Scholar
[57] Frosch R A, Foley H M 1952 Phys. Rev. 88 1337
Google Scholar
[58] Zare R N 1988 Angular Momentum (New York: A Wiley-Interscience Publication) pp186–191
[59] Barclay W L, J r., Anderson M A, Ziurys L M 1993 Astrophys. J. 408 L65
Google Scholar
[60] Sauer B E, Wang J, Hinds E A 1996 J. Chem. Phys. 105 7412
Google Scholar
[61] Brown J H, Carrington A 2012 Rotational Spectroscopy of Diatomic Molecules (Cambridge: Cambridge University Press) pp230–251
[62] Chen T, Bu W, Yan B 2016 Phys. Rev. A 94 063415
Google Scholar
[63] Xu L, Yin Y N, Wei B, Xia Y, Yin J P 2016 Phys. Rev. A 93 013408
Google Scholar
下载:
计量
- 文章访问数: 4108
- PDF下载量: 118
- 被引次数: 0
