-
里德伯原子由于具有较长的能级寿命和易于操控的特点已成为卓越的信息载体之一. 近年来, 关于里德伯原子性质的研究得到逐步的发展和完善, 特别是基于里德伯原子间范德瓦耳斯力诱导的单能级里德伯阻塞和反阻塞效应. 然而, 随着原子间距离的改变, 里德伯相互作用将导致更加复杂的动力学行为. 本文主要研究在原子间距小于其特征长度的情况下, 如何根据构建的里德伯反阻塞及双反阻塞机制一步实现两量子比特控制相位门和交换门, 在此范围内的原子间相互作用将涉及多个能级的布居交换. 数值模拟表明: 里德伯阻塞与双反阻塞机制的解析和数值结果能够达到高度一致, 理想情况下控制相位门和交换门的平均保真度分别为99.35%和99.67%, 此结果对于抵抗高激发里德伯态的自发辐射具有一定的鲁棒性. 希望本文的研究能够为里德伯原子系统中实现大规模容错量子计算提供必要的理论支持与实验依据.Quantum information science is an emerging field that applies the quantum coherence and correlation to cause the revolutionary advances in computation, communication, and fundamental quantum science. As an irreducible ingredient, Rydberg quantum gate is considered to be a powerful resource with great promises to a wide range of quantum information tasks far beyond the original gate proposals, since the remarkable features characterized by Rydberg atom are long lifetime and giant polarizability. In recent years, the research mainly focused on the properties of Rydberg atom, especially for the case where the effects of Rydberg blockade and antiblockade involving single level for each atom are dominated by van der Waals forces. However, with the variation of interatomic distance, Rydberg interactions can induce more complicated dynamical behavior. This paper studies the implementation of controlled-phase gate and swap gate in one step based on the constructed Rydberg antiblockade (RAB) and double antiblockade (RDAB) regimes when the interatomic distance is less than the characteristic length. Different from the conventional RAB regime that requires weak Rydberg-Rydberg interaction (RRI), our attainable strategy is to compensate the RRI-induced energy shift by properly tuning the detuning between the driving field and atomic transition frequencies. In addition, the proposed RDAB mechanism is a new physical insight that can enable two pairs of Rydberg states belonging to different atoms to be excited, simultaneously. In contrast to other blocking schemes or the schemes without requirements for strong interactions, the merits of our proposal lies in the strong dipole-dipole interaction between two atoms, leading to the population exchange of multiple energy levels. Numerical simulations show that the time evolution of the population for collective double-atom basis obtained from the original Hamiltonian agrees well with the analytical results given by the effective Hamiltonian. In the ideal case, the average fidelity of the controlled-phase (swap) gate can reach 99.35% (99.67%) at final time
$t=\sqrt{2}\pi\Delta/\Omega^{2}$ ($t=2\pi\Delta/\Omega^{2}$ ), and our protocol is robustness against spontaneous emission of high-lying Rydberg states. We believe our present investigation is feasible in upcoming experimental realization and may offer an new venue with respect to on-demand design of new types of effective Rydberg quantum gate devices.-
Keywords:
- Rydberg atom /
- anti-blockade regime /
- quantum logic gate /
- dipole-dipole interaction
[1] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) 1–58
[2] Blatt R, Wineland D 2008 Nature 453 1008
Google Scholar
[3] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
Google Scholar
[4] Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Żukowski M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[5] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, Malley P O', Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500
Google Scholar
[6] Jau Y Y, Hankin A M, Keating T, Deutsch I H, Biedermann G W 2016 Nat. Phys. 12 71
Google Scholar
[7] Jaksch D, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[8] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[9] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press) pp1–512
[10] 张秦榕, 王彬彬, 张孟龙, 严冬 2018 67 034202
Google Scholar
Zhang Q R, Wang B B, Zhang M L, Yan D 2018 Acta Phys. Sin. 67 034202
Google Scholar
[11] 张正源, 张天乙, 刘宗凯, 丁冬生, 史保森 2018 69 180301
Zhang Z Y, Zhang T Y, Liu Z K, Ding D S, Shi B S 2018 Acta Phys. Sin. 69 180301
[12] Tong D, Farooqi S M, Stanojevic J, Krishnan S, Zhang Y P, Côté R, Eyler E E, Gould P L 2004 Phys. Rev. Lett. 93 063001
Google Scholar
[13] Omran A, Levine H, Keesling A, Semeghini G, Lukin M D 2019 Science 365 570
Google Scholar
[14] Zheng R H, Kang Y H, Su S L, Song J, Xia Y 2020 Phys. Rev. A 102 012609
Google Scholar
[15] Tebben A, Hainaut C, Walther V, Zhang Y C, Zürn G, Pohl T, Weidemüller M 2019 Phys. Rev. A 100 063812
Google Scholar
[16] Sleator T, Weinfurter H 1995 Phys. Rev. Lett. 74 4087
Google Scholar
[17] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[18] Saffman M, Walker T 2005 Phys. Rev. A 72 022347
Google Scholar
[19] Béguin L, Vernier A, Chicireanu R, Lahaye T, Browaeys A 2013 Phys. Rev. Lett. 110 263201
Google Scholar
[20] Lee T E, Häeffner H, Cross M C 2012 Phys. Rev. Lett. 108 023602
Google Scholar
[21] Zuo Z, Nakagawa K 2010 Phys. Rev. A 82 062328
Google Scholar
[22] Ates C, Pohl T, Pattard T, Rost J M 2007 Phys. Rev. Lett. 98 023002
Google Scholar
[23] Amthor T, Giese C, Hofmann C S, Weidemüller M 2010 Phys. Rev. Lett. 104 013001
Google Scholar
[24] Bai S, Tian X, Han X, Jiao Y, Wu J, Zhao J, Jia S 2020 New J. Phys. 22 013004
Google Scholar
[25] Su S L, Guo F Q, Wu J L, Jin Z, Shao X Q, Zhang S 2020 Europhys. Lett. 131 53001
Google Scholar
[26] Su S L, Tian Y, Shen H Z, Zang H P, Liang E, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[27] Su S L, Gao Y, Liang E, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[28] Bounds A D, Jackson N C, Hanley R K, Bridge E M, Huillery P, Jones M P A 2019 New J. Phys. 21 053026
Google Scholar
[29] Young J T, Boulier T, Magnan E, Goldschmidt E A, Wilson R M, Rolston S L, Porto J V, Gorshkov A V 2018 Phys. Rev. A 97 023424
Google Scholar
[30] Su S L, Liang E, Zhang S, Wen J J, Sun L L, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[31] Su S L, Shen H Z, Liang E, Zhang S 2018 Phys. Rev. A 98 032306
Google Scholar
[32] Wu J L, Song J, Su S L 2020 Phys. Lett. A 384 126039
Google Scholar
[33] Li D X, Shao X Q, Wu J H, Yi X X 2017 Opt. Lett. 42 3904
Google Scholar
[34] Shao X Q, Wu J H, Yi X X 2017 Phys. Rev. A 95 062339
Google Scholar
[35] Zuo Z, Nakagawa K 2010 Physical Review A 82 062328
[36] Lee T E, Häffner H, Cross M C 2012 Physical Review Letters 108 023602
[37] Carr A W, Saffman M 2013 Phys. Rev. Lett. 111 033607
Google Scholar
[38] Li W, Ates C, Lesanovsky I 2013 Phys. Rev. Lett. 110 213005
Google Scholar
[39] Ravets S, Labuhn H, Barredo D, Béguin L, Lahaye T, Browaeys A 2014 Nat. Phys. 10 914
Google Scholar
[40] Ravets S, Labuhn H, Barredo D, Béguin L, Lahaye T, Browaeys A 2015 Phys. Rev. A 92 020701(R
Google Scholar
[41] Walker T G, Saffman M 2005 J. Phys. B 38 S309
Google Scholar
[42] Walker T G, Saffman M 2008 Phys. Rev. A 77 032723
Google Scholar
[43] Browaeys A, Barredo D, Lahaye T 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152001
Google Scholar
[44] Ates C, Eisfeld A, Rost J M 2008 New J. Phys. 10 045030
Google Scholar
[45] Anderson W R, Veale J R, Gallagher T F 1998 Phys. Rev. Lett. 80 249
Google Scholar
[46] Gorniaczyk H, Tresp C, Bienias P, Paris-Mandoki A, Li W, Mirgorodskiy I, Büchler H P, Lesanovsky I, Hofferberth S 2016 Nat. Commun. 7 12480
Google Scholar
[47] Beterov I I, Saffman M, Yakshina E A, Tretyakov D B, Entin V M, Bergamini S, Kuznetsova E A, Ryabtsev I I 2016 Phys. Rev. A 94 062307
Google Scholar
[48] Beterov I I, Ashkarin I N, Yakshina E A, Tretyakov D B, Entin V M, Ryabtsev I I, Cheinet P, Pillet P, Saffman M 2018 Phys. Rev. A 98 042704
Google Scholar
[49] Shao X Q 2020 Phys. Rev. A 102 053118
Google Scholar
[50] James D F V, Jerke J 2007 Can. J. Phys. 85 625
Google Scholar
[51] Yi X X, Cui B, Wu C, Oh C H 2011 J. Phys. B: At. Mol. Opt. Phys. 44 165503
Google Scholar
[52] Yin Z Q, Li F L 2007 Phys. Rev. A 75 012324
Google Scholar
[53] Müller M M, Murphy M, Montangero S, Calarco T, Grangier P, Browaeys A 2014 Phys. Rev. A 89 032334
Google Scholar
-
图 1 里德伯原子的能级结构.
$ |p(0)\rangle_{\xi} $ 和$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ )代表两个激发(基)态, 具有相同拉比频率的两束非共振的光学激光分别驱动对应原子的跃迁$ |1\rangle_{1}\leftrightarrow|p\rangle_{1} $ 和$ |1\rangle_{2}\leftrightarrow|d\rangle_{2} $ , 失谐量为$\varDelta$ .$ V_{pd} $ 表示两个里德伯原子间共振的偶极-偶极相互作用强度Fig. 1. Energy-level configuration of Rydberg atoms.
$ |p(0)\rangle_{\xi} $ and$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ ) represent two Rydberg (ground) states, off-resonance optical lasers drive the transitions$ |1\rangle_{1}\leftrightarrow|p\rangle_{1} $ and$ |1\rangle_{2}\leftrightarrow|d\rangle_{2} $ for the corresponding atom with identical Rabi frequency$\varOmega$ and detuning$\varDelta$ , respectively.$ V_{pd} $ denotes the strength of resonant diploe-diploe interaction between two Rydberg atoms.
图 2 (a) 态矢量
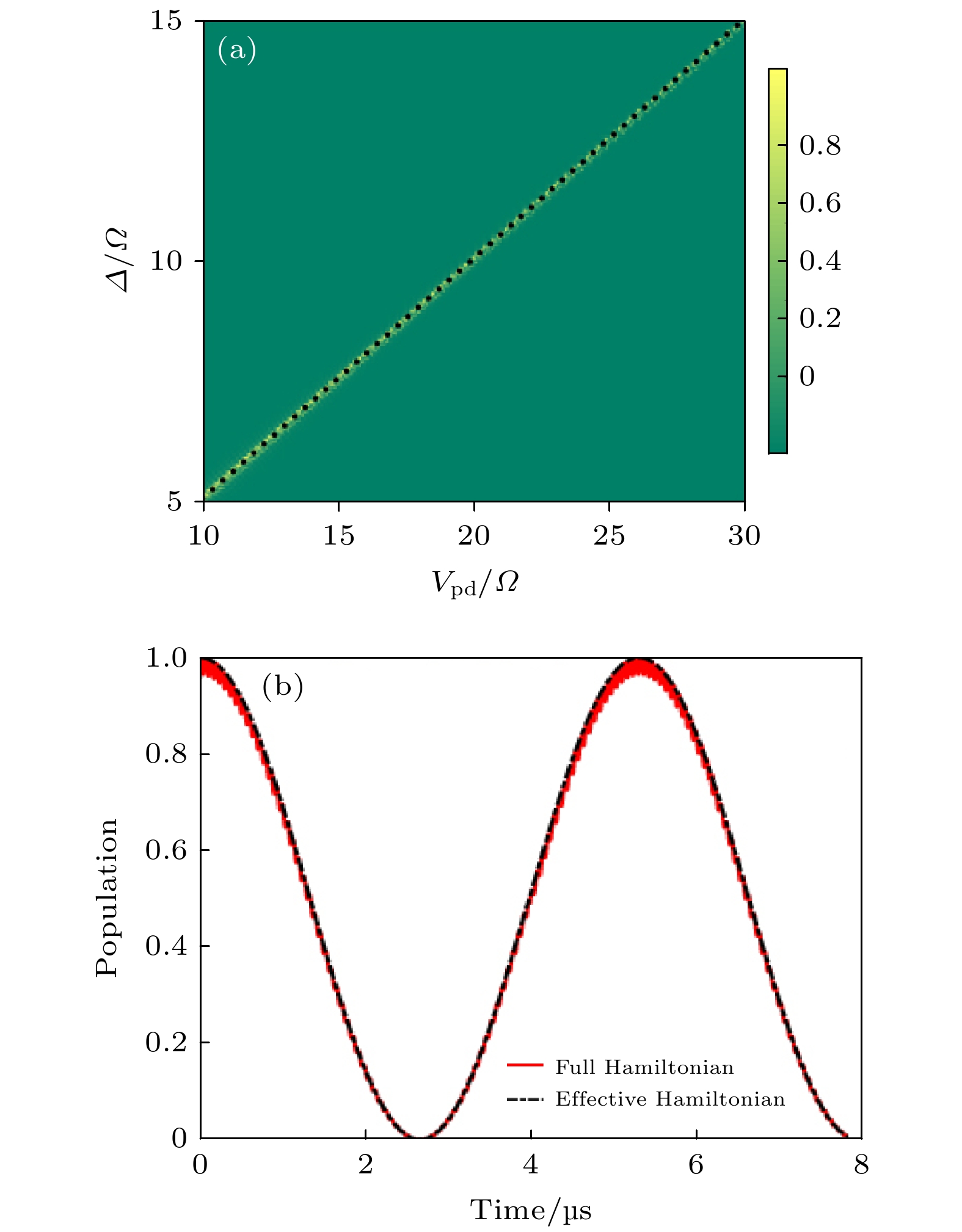
$ |+\rangle $ 的布居在时刻$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ 随着参数$ V_{pd}/\varOmega $ 和$ \varDelta/\varOmega $ 的变化, 系统初态为$ |11\rangle $ , 图中的黑色点线是利用$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ 得到的解析结果; (b) 由原始哈密顿量(黑色点划线)以及有效哈密顿量(红色实线)支配的布居动力学随时间的演化, 系统的初态和末态分别为$ |11\rangle $ 和$-|11\rangle$ , 相关的系统参数设置为:$ \varOmega/(2\pi) $ = 2 MHz,$\varDelta = 7.5 \; \Omega$ , 以及$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ Fig. 2. (a) Population of state
$ |+\rangle $ versus$ V_{pd}/\varOmega $ and$ \varDelta/\varOmega $ at the time$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ with a fixed initial state$ |11\rangle $ , the solid dots are analytical results based on the equation$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ ; (b) populations of$-|11\rangle$ versus the evolution time from the initial state$ |11\rangle $ governed by Full Hamiltonian (black dash-dotted line) and effective Hamiltonian (red solid line), the related parameters are chosen as:$\varOmega/(2\pi)$ = 2 MHz,$\varDelta = 7.5\;\Omega$ , and$V_{pd} = $ $ 2\varDelta+\varOmega^{2}/(4\varDelta)$ .
图 3 里德伯原子的能级结构.
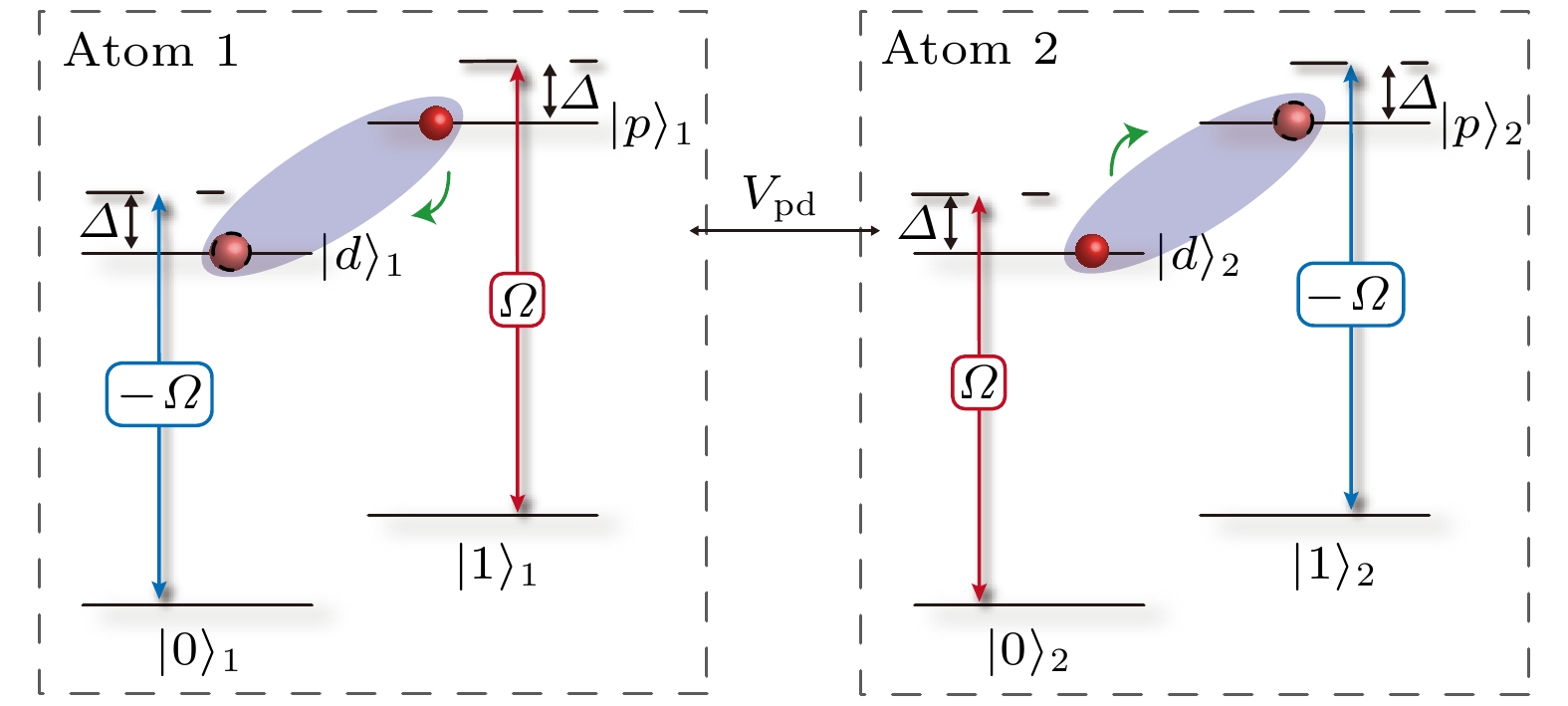
$ |p(0)\rangle_{\xi} $ 和$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ )代表两个激发(基)态, 两束具有相同拉比频率$ \varOmega $ 及相对相位为$ \theta_{\xi} $ 的非共振的光学激光分别驱动对应原子的跃迁$ |0\rangle_{\xi}\leftrightarrow|d\rangle_{\xi} $ 和$ |1\rangle_{\xi}\leftrightarrow|p\rangle_{\xi} $ , 失谐量为$ \varDelta $ .$ V_{pd} $ 表示两个里德伯原子间共振的偶极-偶极相互作用强度Fig. 3. Energy-level configuration of Rydberg atoms.
$ |p(0)\rangle_{\xi} $ and$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ ) represent two Rydberg (ground) states, off-resonance optical lasers drive the transitions$ |0\rangle_{\xi}\leftrightarrow|d\rangle_{\xi} $ and$ |1\rangle_{\xi}\leftrightarrow|p\rangle_{\xi} $ for the corresponding atom with identical Rabi frequency$ \varOmega $ , detuning$ \varDelta $ , and different relative phase$ \theta_{\xi} $ , respectively.$ V_{pd} $ denotes the strength of resonant diploe-diploe interaction between two Rydberg atoms.
图 4 (a) 态矢量
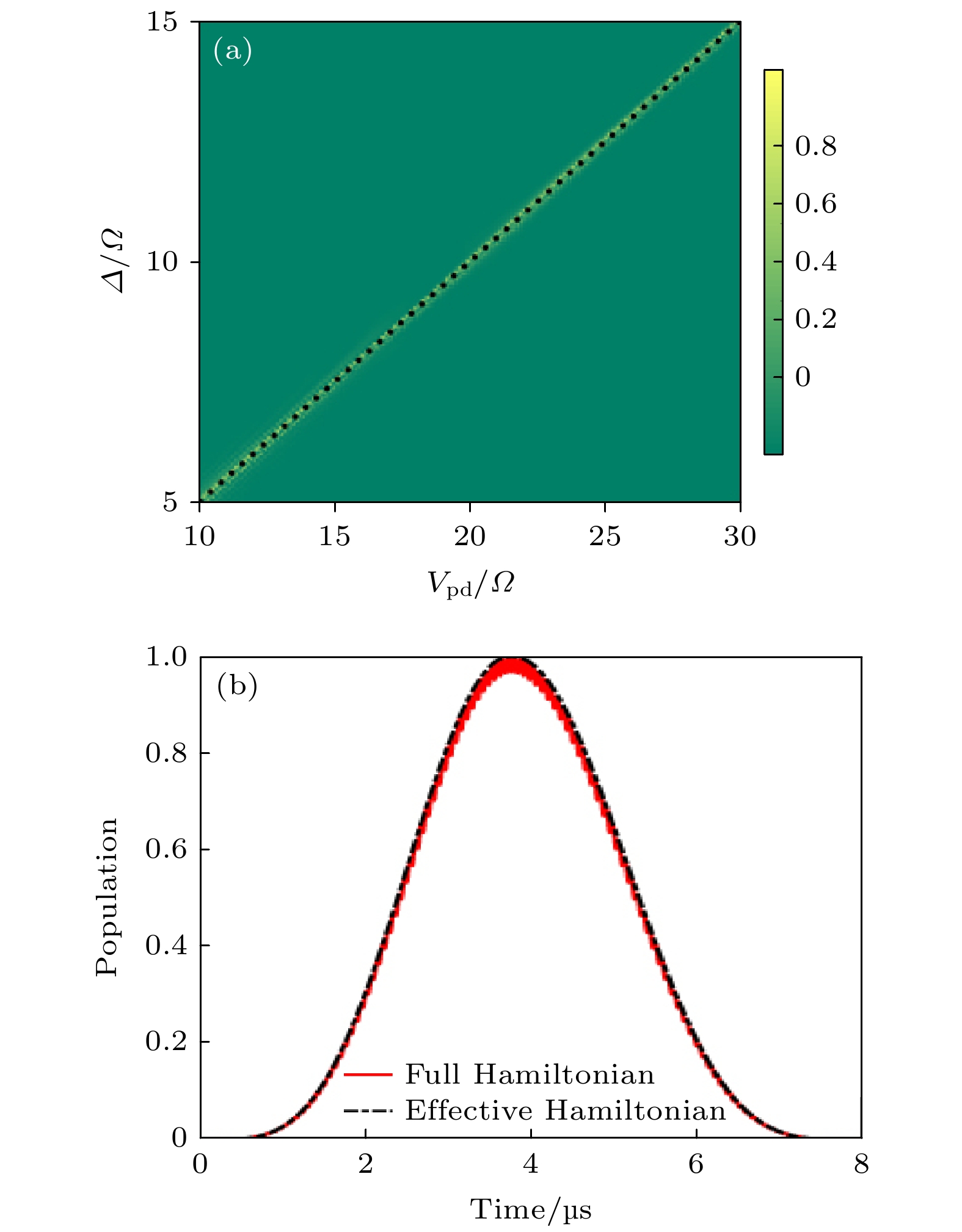
$ |+\rangle $ 的布居在时刻$ t = \pi\varDelta/\varOmega^{2} $ 随着参数$ V_{pd}/\varOmega $ 和$ \varDelta/\varOmega $ 的变化, 系统初态为$|G\rangle = 1/\sqrt{2}(|10\rangle- $ $ |01\rangle)$ , 图中的黑色点线是利用公式$ V_{pd} = 2\varDelta $ 得到的解析结果; (b) 由原始哈密顿量(黑色点划线)以及有效哈密顿量(红色实线)支配的布居动力学随时间的演化, 系统的初态和末态分别为$ |10\rangle $ 和$ |01\rangle $ , 相关的系统参数设置为:$ \varOmega/(2\pi) $ = 2 MHz,$\varDelta = 7.5\;\Omega$ , 以及$ V_{pd} = 2\varDelta $ Fig. 4. (a) Population of state
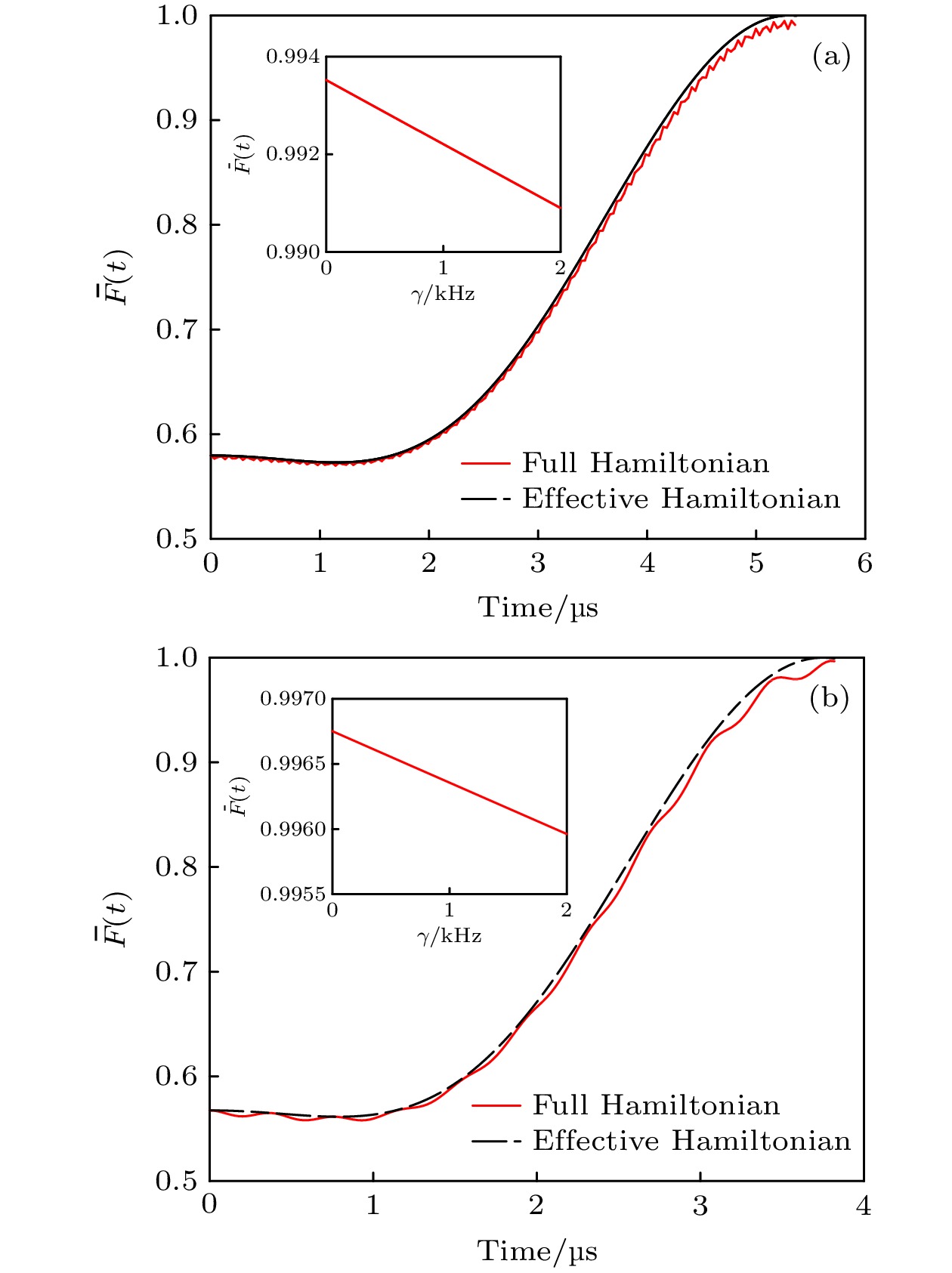
$ |+\rangle $ versus$ V_{pd}/\varOmega $ and$ \varDelta/\varOmega $ at the time$ t = \pi\varDelta/\varOmega^{2} $ with a fixed initial state$ |10\rangle $ , the solid dots are analytical results based on the equation$ V_{pd} = 2\varDelta $ ; (b) populations of$ |01\rangle $ versus the evolution time from the initial state$ |10\rangle $ governed by Full Hamiltonian (black dash-dotted line) and effective Hamiltonian (red solid line), the related parameters are chosen as:$\varOmega/(2\pi)$ = 2 MHz,$\varDelta = 7.5\;\Omega$ , and$ V_{pd} = 2\varDelta $ .
图 5 由原始哈密顿量和有效哈密顿量支配的平均保真度随时间的演化 (a)控制相位门; (b)控制交换门. 系统参数为
$ \varOmega/(2\pi) $ = 2 MHz,$\varDelta = 7.5\varOmega$ ,$V_{pd} = 2\varDelta+ \varOmega^{2}/(4\varDelta)$ ($V_{pd} = $ $ 2\varDelta$ ) 以及$ \gamma $ = 0 kHz. 插图表示不同的原子自发辐射率对平均保真度的影响, 选定的末态时刻为$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ ($ t = 2\pi\varDelta/\varOmega^{2} $ ), 其他的系统参数除了$ \gamma $ 以外均与大图相同Fig. 5. Time-dependence of the average fidelity dominated by full Hamiltonian and effective Hamiltonian: (a) controlled-PHASE gate; (b) controlled-SWAP gate. Values of parameters are:
$ \varOmega/(2\pi) $ = 2 MHz,$\varDelta = 7.5\;\Omega$ ,$V_{pd} = 2\varDelta+ $ $ \varOmega^{2}/(4\varDelta)$ ($ V_{pd} = 2\varDelta $ ) and$ \gamma $ = 0 kHz. The insets shows the influence of different atomic decay rates$ \gamma $ on the final average fidelity. The chosen final time is$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ ($ t = 2\pi\varDelta/\varOmega^{2} $ ) and the other parameters are the same as in panels (a) and (b) except for$ \gamma $ . -
[1] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) 1–58
[2] Blatt R, Wineland D 2008 Nature 453 1008
Google Scholar
[3] Specht H P, Nölleke C, Reiserer A, Uphoff M, Figueroa E, Ritter S, Rempe G 2011 Nature 473 190
Google Scholar
[4] Pan J W, Chen Z B, Lu C Y, Weinfurter H, Zeilinger A, Żukowski M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[5] Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, Malley P O', Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500
Google Scholar
[6] Jau Y Y, Hankin A M, Keating T, Deutsch I H, Biedermann G W 2016 Nat. Phys. 12 71
Google Scholar
[7] Jaksch D, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 85 2208
Google Scholar
[8] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[9] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press) pp1–512
[10] 张秦榕, 王彬彬, 张孟龙, 严冬 2018 67 034202
Google Scholar
Zhang Q R, Wang B B, Zhang M L, Yan D 2018 Acta Phys. Sin. 67 034202
Google Scholar
[11] 张正源, 张天乙, 刘宗凯, 丁冬生, 史保森 2018 69 180301
Zhang Z Y, Zhang T Y, Liu Z K, Ding D S, Shi B S 2018 Acta Phys. Sin. 69 180301
[12] Tong D, Farooqi S M, Stanojevic J, Krishnan S, Zhang Y P, Côté R, Eyler E E, Gould P L 2004 Phys. Rev. Lett. 93 063001
Google Scholar
[13] Omran A, Levine H, Keesling A, Semeghini G, Lukin M D 2019 Science 365 570
Google Scholar
[14] Zheng R H, Kang Y H, Su S L, Song J, Xia Y 2020 Phys. Rev. A 102 012609
Google Scholar
[15] Tebben A, Hainaut C, Walther V, Zhang Y C, Zürn G, Pohl T, Weidemüller M 2019 Phys. Rev. A 100 063812
Google Scholar
[16] Sleator T, Weinfurter H 1995 Phys. Rev. Lett. 74 4087
Google Scholar
[17] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[18] Saffman M, Walker T 2005 Phys. Rev. A 72 022347
Google Scholar
[19] Béguin L, Vernier A, Chicireanu R, Lahaye T, Browaeys A 2013 Phys. Rev. Lett. 110 263201
Google Scholar
[20] Lee T E, Häeffner H, Cross M C 2012 Phys. Rev. Lett. 108 023602
Google Scholar
[21] Zuo Z, Nakagawa K 2010 Phys. Rev. A 82 062328
Google Scholar
[22] Ates C, Pohl T, Pattard T, Rost J M 2007 Phys. Rev. Lett. 98 023002
Google Scholar
[23] Amthor T, Giese C, Hofmann C S, Weidemüller M 2010 Phys. Rev. Lett. 104 013001
Google Scholar
[24] Bai S, Tian X, Han X, Jiao Y, Wu J, Zhao J, Jia S 2020 New J. Phys. 22 013004
Google Scholar
[25] Su S L, Guo F Q, Wu J L, Jin Z, Shao X Q, Zhang S 2020 Europhys. Lett. 131 53001
Google Scholar
[26] Su S L, Tian Y, Shen H Z, Zang H P, Liang E, Zhang S 2017 Phys. Rev. A 96 042335
Google Scholar
[27] Su S L, Gao Y, Liang E, Zhang S 2017 Phys. Rev. A 95 022319
Google Scholar
[28] Bounds A D, Jackson N C, Hanley R K, Bridge E M, Huillery P, Jones M P A 2019 New J. Phys. 21 053026
Google Scholar
[29] Young J T, Boulier T, Magnan E, Goldschmidt E A, Wilson R M, Rolston S L, Porto J V, Gorshkov A V 2018 Phys. Rev. A 97 023424
Google Scholar
[30] Su S L, Liang E, Zhang S, Wen J J, Sun L L, Jin Z, Zhu A D 2016 Phys. Rev. A 93 012306
Google Scholar
[31] Su S L, Shen H Z, Liang E, Zhang S 2018 Phys. Rev. A 98 032306
Google Scholar
[32] Wu J L, Song J, Su S L 2020 Phys. Lett. A 384 126039
Google Scholar
[33] Li D X, Shao X Q, Wu J H, Yi X X 2017 Opt. Lett. 42 3904
Google Scholar
[34] Shao X Q, Wu J H, Yi X X 2017 Phys. Rev. A 95 062339
Google Scholar
[35] Zuo Z, Nakagawa K 2010 Physical Review A 82 062328
[36] Lee T E, Häffner H, Cross M C 2012 Physical Review Letters 108 023602
[37] Carr A W, Saffman M 2013 Phys. Rev. Lett. 111 033607
Google Scholar
[38] Li W, Ates C, Lesanovsky I 2013 Phys. Rev. Lett. 110 213005
Google Scholar
[39] Ravets S, Labuhn H, Barredo D, Béguin L, Lahaye T, Browaeys A 2014 Nat. Phys. 10 914
Google Scholar
[40] Ravets S, Labuhn H, Barredo D, Béguin L, Lahaye T, Browaeys A 2015 Phys. Rev. A 92 020701(R
Google Scholar
[41] Walker T G, Saffman M 2005 J. Phys. B 38 S309
Google Scholar
[42] Walker T G, Saffman M 2008 Phys. Rev. A 77 032723
Google Scholar
[43] Browaeys A, Barredo D, Lahaye T 2016 J. Phys. B: At. Mol. Opt. Phys. 49 152001
Google Scholar
[44] Ates C, Eisfeld A, Rost J M 2008 New J. Phys. 10 045030
Google Scholar
[45] Anderson W R, Veale J R, Gallagher T F 1998 Phys. Rev. Lett. 80 249
Google Scholar
[46] Gorniaczyk H, Tresp C, Bienias P, Paris-Mandoki A, Li W, Mirgorodskiy I, Büchler H P, Lesanovsky I, Hofferberth S 2016 Nat. Commun. 7 12480
Google Scholar
[47] Beterov I I, Saffman M, Yakshina E A, Tretyakov D B, Entin V M, Bergamini S, Kuznetsova E A, Ryabtsev I I 2016 Phys. Rev. A 94 062307
Google Scholar
[48] Beterov I I, Ashkarin I N, Yakshina E A, Tretyakov D B, Entin V M, Ryabtsev I I, Cheinet P, Pillet P, Saffman M 2018 Phys. Rev. A 98 042704
Google Scholar
[49] Shao X Q 2020 Phys. Rev. A 102 053118
Google Scholar
[50] James D F V, Jerke J 2007 Can. J. Phys. 85 625
Google Scholar
[51] Yi X X, Cui B, Wu C, Oh C H 2011 J. Phys. B: At. Mol. Opt. Phys. 44 165503
Google Scholar
[52] Yin Z Q, Li F L 2007 Phys. Rev. A 75 012324
Google Scholar
[53] Müller M M, Murphy M, Montangero S, Calarco T, Grangier P, Browaeys A 2014 Phys. Rev. A 89 032334
Google Scholar
下载:
计量
- 文章访问数: 5621
- PDF下载量: 136
- 被引次数: 0
