椭球胶体在圆球胶体体系中扩散行为的实验研究

刘心卓; 王华光

doi:10.7498/aps.69.20201301

摘要

复杂受限介质中的扩散行为在自然界是普遍存在的, 与其相关的研究涉及物理学、材料科学和生物学等多学科领域, 受到了这些领域研究者们的广泛关注. 然而, 相比于众多的圆球受限扩散研究, 对形状各向异性的粒子在复杂受限介质中的扩散行为的研究依然比较匮乏. 本文提出了一个简单的软物质实验模型—胶体椭球与圆球混合体系, 来研究形状各向异性的椭球在圆球的受限环境下的扩散行为. 通过描述椭球的运动轨迹和计算粒子的均方位移、范霍夫自关联函数以及非高斯参量, 发现随着圆球浓度的增大, 椭球的平动和转动都被抑制, 出现次扩散行为; 并且, 平动和转动的位移分布也展现出不同的演化行为, 表明这两种运动在高浓度下会发生解耦合. 此外, 在不同圆球浓度下, 椭球都趋向于沿自身长轴方向扩散, 因此在沿长轴和短轴方向的平动受到的受限作用的影响也不同, 导致二者也发生解耦合行为. 综上所述, 受限环境会导致各向异性胶体粒子出现反常扩散行为. 本文的研究有助于理解复杂环境中各向异性物体的扩散和输运行为.

关键词:

胶体 /
扩散 /
椭球 /
非高斯行为 /
动力学

Abstract

The diffusive transport in complex confined media is ubiquitous such as diffusions of micro- or nano-particles in glassy liquids and polymer solutions, protein diffusions under crowded conditions, and deliveries of drugs in the biological media. Therefore, the understanding of the diffusive transport arouses the great interest of researchers in the physics, materials science, and biology circles. Despite the fact that the shape of the colloidal particles acts as one of the important physical factors influencing their dynamic behaviors, the study of the anisotropic particles diffusing in confined media is still lacking. In this work, we propose a simple experimental model to investigate the confined diffusion of shape-anisotropic particles. The diffusion of an ellipsoid at different area fractions (ϕ) of colloidal spheres is investigated through video microscopy. At low ϕ, ellipsoid exhibits a random trajectory and free diffusion in translational and rotational degree of freedom; while at high ϕ, the trajectory is in a small spatial range with a nearly constant orientation of the particle, indicating that the arrested diffusion takes place in translational and rotational degree of freedom. The translational and rotational mean square displacement decrease with the increase of ϕ. By power-law fitting (~t^β), it is found that β decreases from 1 to a small value at high ϕ, demonstrating that the ellipsoid experiences a transition from normal diffusion to sub-diffusion. Moreover, β for rotational motion decreases faster than that for translational motion at high ϕ, which signifies that the the rotational motion decouples from the translational motion with increasing ϕ. The results from the van Hove correlation function show that the translational displacement along the major axis of the ellipsoid is always larger than that along the minor axis, manifesting the ellipsoid prefers to diffuse along its major axis independent of ϕ. Significant non-Gaussian tail is observed in the distribution of the translational displacement along the major axis with increasing ϕ. However, the distribution of the translational displacement along the minor axis presents a nearly Gaussian behavior independent of ϕ. This indicates that the translational motion along the major axis decouples from the translational motion along the minor with increasing ϕ. For the rotational displacement, the non-Gaussian tail is only observed at the intermediate ϕ. These non-Gaussian behaviors are confirmed by calculating the non-Gaussian parameter (α₂). Our experiments demonstrate that the confinements give rise to the anomalous diffusion behaviors of the anisotropic colloids, which is conducive to the understanding of transportations of anisotropic objects in complex environments.

Keywords:

作者及机构信息

刘心卓¹,
王华光^1,2

1.
苏州大学, 软凝聚态物理及交叉研究中心, 苏州　215006

2.
苏州大学材料与化学化工学部, 苏州　215123

通信作者: 王华光, hgwang@suda.edu.cn

基金项目: 国家自然科学基金(批准号: 11704269)和江苏省高等学校自然科学研究项目(批准号: 17KJB140020)资助的课题

Authors and contacts

1.
Centre for Soft Condensed Matter Physics and Interdisciplinary Research, Soochow University, Suzhou 215006, China

2.
College of Chemistry, Chemical Engineering and Materials Science, Soochow University, Suzhou 215123, China

Corresponding author: Wang Hua-Guang, hgwang@suda.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11704269) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 17KJB140020)

文章全文 : translate this paragraph

参考文献

[1]	Wang Y, Benton L A, Singh V, Pielak G J 2012 J. Phys. Chem. Lett. 3 2703 Google Scholar
[2]	Grimaldo M, Lopez H, Beck C, Roosen R F, Moulin M, Devos J M, Laux V, Hartlein M, Da Vela S, Schweins R, Mariani A, Zhang F, Barrat J L, Oettel M, Forsyth V T, Seydel T, Schreiber F 2019 J. Phys. Chem. Lett. 10 1709 Google Scholar
[3]	Edmond K V, Elsesser M T, Hunter G L, Pine D J, Weeks E R 2012 P. Natl. Acad. Sci. U.S.A. 109 17891 Google Scholar
[4]	Sentjabrskaja T, Zaccarelli E, De Michele C, Sciortino F, Tartaglia P, Voigtmann T, Egelhaaf S U, Laurati M 2016 Nat. Commun. 7 11133 Google Scholar
[5]	Xue C, Zheng X, Chen K, Tian Y, Hu G 2016 J. Phys. Chem. Lett. 7 514 Google Scholar
[6]	Wang X, Chen Y, Xue L, Pothayee N, Zhang R, Riffle J S, Reineke T M, Madsen L A 2014 J. Phys. Chem. Lett. 5 3825 Google Scholar
[7]	Geng Y, Dalhaimer P, Cai S, Tsai R, Tewari M, Minko T, Discher D E 2007 Nat. Nanotechnol. 2 249 Google Scholar
[8]	Mitragotri S, Lahann J 2009 Nat. Mater. 8 15 Google Scholar
[9]	Hnggi P, Marchesoni F 2009 Rev. Mod. Phys. 81 387 Google Scholar
[10]	Zhou H X, Rivas G, Minton A P 2008 Annu. Rev. Biophys. 37 375 Google Scholar
[11]	Weeks E R, Crocker J C, Levitt A C, Schofield A, Weitz D A 2000 Science 287 627 Google Scholar
[12]	Chen J X, Chen Y G, Ma Y Q 2016 Soft Matter 12 1876 Google Scholar
[13]	Chen J X, Zhu J X, Ma Y Q, Cao J S 2014 Epl-Europhys. Lett. 106 18003 Google Scholar
[14]	Glotzer S C, Solomon M J 2007 Nat. Mater. 16 557 Google Scholar
[15]	Champion J A, Katare Y K, Mitragotri S 2007 P. Natl. Acad. Sci. U.S.A. 104 11901 Google Scholar
[16]	Han Y, Alsayed A M, Nobili M, Zhang J, Lubensky T C, Yodh A G 2006 Science 314 626 Google Scholar
[17]	Chakrabarty A, Konya A, Wang F, Selinger J V, Sun K, Wei Q H 2013 Phys. Rev. Lett. 111 160603 Google Scholar
[18]	Moreno A J, Kob W 2004 AIP Conference Proceedings 708 576 Google Scholar
[19]	Kim J, Sung B J 2015 Phys. Rev. Lett. 115 158302 Google Scholar
[20]	Sakha F, Fazli H 2010 J. Chem. Phys. 133 234904 Google Scholar
[21]	Ho C C, Keller A, Odell J A, Ottewill R H 1993 Colloid Polym. Sci. 271 469 Google Scholar
[22]	Zheng Z, Wang F, Han Y 2011 Phys. Rev. Lett. 107 065702 Google Scholar

施引文献

图 1 (a)样品在显微镜物镜上的示意图; (b) ϕ = 0.57的样品的显微镜照片

Fig. 1. (a) Schematic of the experimental sample on a microscope objective; (b) a bright-field microscope image of the colloidal suspension for ϕ = 0.57.

下载: 全尺寸图片幻灯片

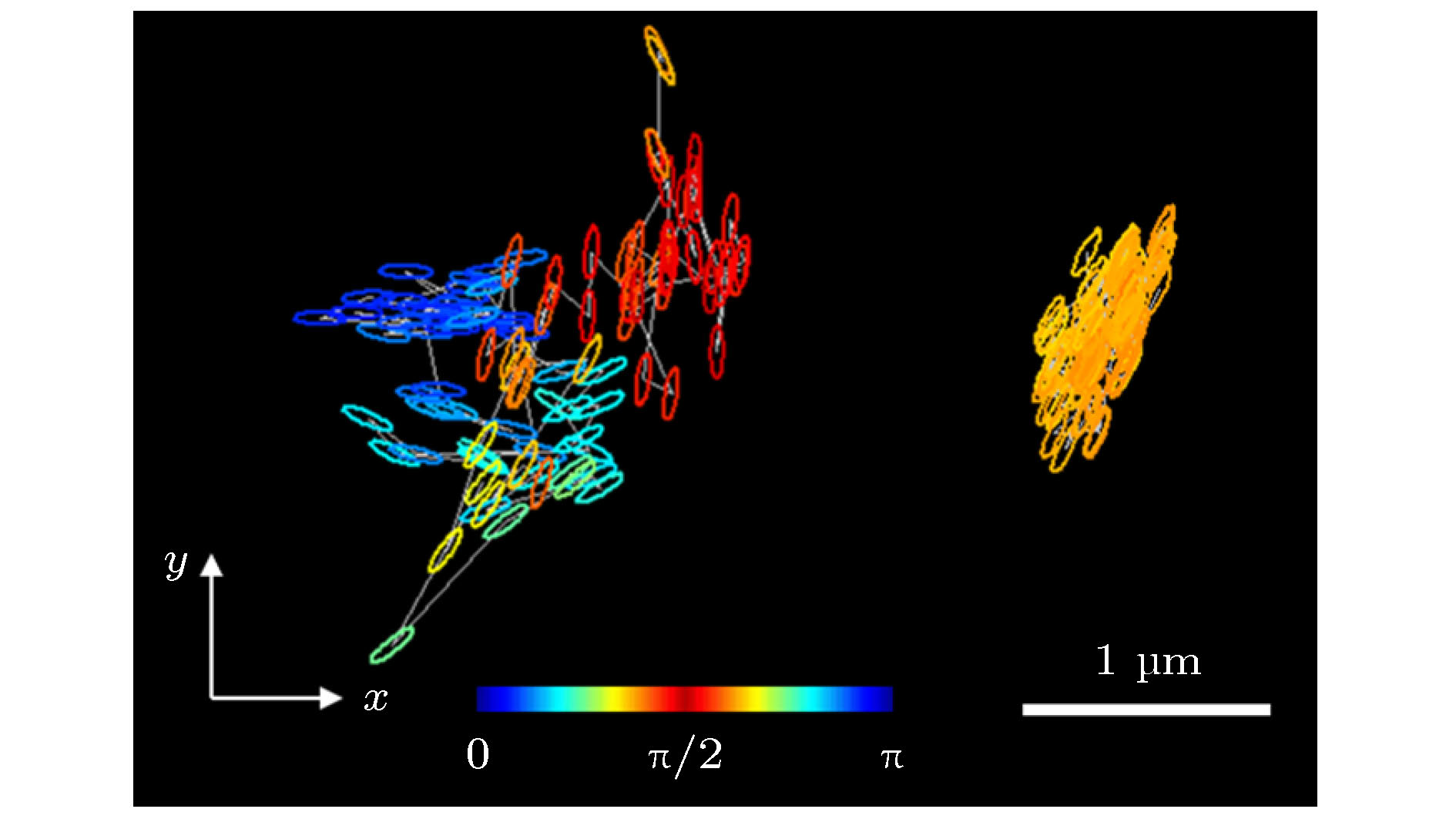
图 2 椭球在不同圆球浓度下运动100 s的轨迹: ϕ = 0.57(左)和ϕ = 0.81(右). 椭球的不同时刻位置用空心椭圆表示, 其取向是椭球长轴方向和x轴方向的夹角, 用颜色表示

Fig. 2. 100 s trajectories of an ellipsoid at ϕ = 0.57 (left panel) and ϕ = 0.81 (right panel). The positions of the particle at different times are indicated by ellipses. The color indicates the orientation of the particle with respect to the x axis.

下载: 全尺寸图片幻灯片

图 3 椭球在不同ϕ下的平动均方位移(a)和转动均方位移(b), 实线是时间范围为1−20 s的幂律拟合, ～t^β

Fig. 3. Translational mean square displacements (a) and rotational mean square displacements (b) of ellipsoids at different ϕ. Solid lines are the power-law fits: ～t^β in the time range of 1−20 s.

下载: 全尺寸图片幻灯片

图 4 平动和转动扩散指数β随浓度的变化

Fig. 4. The ϕ dependent β for translational and rotational motions.

下载: 全尺寸图片幻灯片

图 5 椭球在不同ϕ运动4 s的位移分布　(a)沿长轴方向平动位移; (b)沿短轴方向平动位移; (c)转动位移. 实线是高斯拟合

Fig. 5. The distribution of the ellipsoid displacement for lag time of 4 s at different ϕ: (a) Translational displacement along the long axis of the ellipsoid; (b) translational displacement along the short axis, (c) rotational displacement. Solid lines are the best Gaussian fits.

下载: 全尺寸图片幻灯片

图 6 椭球运动4 s沿长轴平动位移 (r_//), 沿短轴平动位移 (r_⊥) 和转动位移 (θ) 的非高斯参量

Fig. 6. The non-Gauss parameter of the displacement of ellipsoid for lag time of 4 s: Translational displacement along the long axis of the ellipsoid (r_//), translational displacement along the short axis (r_⊥), and rotational displacement (θ).

下载: 全尺寸图片幻灯片

map

[1]	Wang Y, Benton L A, Singh V, Pielak G J 2012 J. Phys. Chem. Lett. 3 2703 Google Scholar
[2]	Grimaldo M, Lopez H, Beck C, Roosen R F, Moulin M, Devos J M, Laux V, Hartlein M, Da Vela S, Schweins R, Mariani A, Zhang F, Barrat J L, Oettel M, Forsyth V T, Seydel T, Schreiber F 2019 J. Phys. Chem. Lett. 10 1709 Google Scholar
[3]	Edmond K V, Elsesser M T, Hunter G L, Pine D J, Weeks E R 2012 P. Natl. Acad. Sci. U.S.A. 109 17891 Google Scholar
[4]	Sentjabrskaja T, Zaccarelli E, De Michele C, Sciortino F, Tartaglia P, Voigtmann T, Egelhaaf S U, Laurati M 2016 Nat. Commun. 7 11133 Google Scholar
[5]	Xue C, Zheng X, Chen K, Tian Y, Hu G 2016 J. Phys. Chem. Lett. 7 514 Google Scholar
[6]	Wang X, Chen Y, Xue L, Pothayee N, Zhang R, Riffle J S, Reineke T M, Madsen L A 2014 J. Phys. Chem. Lett. 5 3825 Google Scholar
[7]	Geng Y, Dalhaimer P, Cai S, Tsai R, Tewari M, Minko T, Discher D E 2007 Nat. Nanotechnol. 2 249 Google Scholar
[8]	Mitragotri S, Lahann J 2009 Nat. Mater. 8 15 Google Scholar
[9]	Hnggi P, Marchesoni F 2009 Rev. Mod. Phys. 81 387 Google Scholar
[10]	Zhou H X, Rivas G, Minton A P 2008 Annu. Rev. Biophys. 37 375 Google Scholar
[11]	Weeks E R, Crocker J C, Levitt A C, Schofield A, Weitz D A 2000 Science 287 627 Google Scholar
[12]	Chen J X, Chen Y G, Ma Y Q 2016 Soft Matter 12 1876 Google Scholar
[13]	Chen J X, Zhu J X, Ma Y Q, Cao J S 2014 Epl-Europhys. Lett. 106 18003 Google Scholar
[14]	Glotzer S C, Solomon M J 2007 Nat. Mater. 16 557 Google Scholar
[15]	Champion J A, Katare Y K, Mitragotri S 2007 P. Natl. Acad. Sci. U.S.A. 104 11901 Google Scholar
[16]	Han Y, Alsayed A M, Nobili M, Zhang J, Lubensky T C, Yodh A G 2006 Science 314 626 Google Scholar
[17]	Chakrabarty A, Konya A, Wang F, Selinger J V, Sun K, Wei Q H 2013 Phys. Rev. Lett. 111 160603 Google Scholar
[18]	Moreno A J, Kob W 2004 AIP Conference Proceedings 708 576 Google Scholar
[19]	Kim J, Sung B J 2015 Phys. Rev. Lett. 115 158302 Google Scholar
[20]	Sakha F, Fazli H 2010 J. Chem. Phys. 133 234904 Google Scholar
[21]	Ho C C, Keller A, Odell J A, Ottewill R H 1993 Colloid Polym. Sci. 271 469 Google Scholar
[22]	Zheng Z, Wang F, Han Y 2011 Phys. Rev. Lett. 107 065702 Google Scholar

[1]	梁建, 王华光, 张泽新. 粗糙和光滑椭球胶体的受限扩散. , 2024, 73(14): 148202. doi: 10.7498/aps.73.20240559
[2]	高艺雯, 王影, 田文得, 陈康. 空间调制的驱动外场下活性聚合物的动力学行为. , 2022, 71(24): 240501. doi: 10.7498/aps.71.20221367
[3]	黄多辉, 万明杰, 杨俊升. 聚甲基丙烯酸甲酯与碳纳米管纳米复合材料玻璃化转变及其非线性力学行为的分子动力学模拟. , 2021, 70(21): 218101. doi: 10.7498/aps.70.20210752
[4]	贝帮坤, 王华光, 张泽新. 有限尺寸胶体体系的二维结晶. , 2019, 68(10): 106401. doi: 10.7498/aps.68.20190304
[5]	张恒, 黄燕, 石旺舟, 周孝好, 陈效双. Al原子在Si表面扩散动力学的第一性原理研究. , 2019, 68(20): 207302. doi: 10.7498/aps.68.20190783
[6]	孙艳丽, 王华光, 张泽新. 椭球与圆球混合胶体体系的玻璃化转变. , 2018, 67(10): 106401. doi: 10.7498/aps.67.20180264
[7]	陈科. 胶体在非晶研究中的应用. , 2017, 66(17): 178201. doi: 10.7498/aps.66.178201
[8]	马红孺. 胶体排空相互作用理论与计算. , 2016, 65(18): 184701. doi: 10.7498/aps.65.184701
[9]	张天辉, 曹镜声, 梁颖, 刘向阳. 胶体在基础物理研究中的应用. , 2016, 65(17): 176401. doi: 10.7498/aps.65.176401
[10]	高雪云, 王海燕, 李春龙, 任慧平, 李德超, 刘宗昌. 稀土La对bcc-Fe中Cu扩散行为影响的第一性原理研究. , 2014, 63(24): 248101. doi: 10.7498/aps.63.248101
[11]	戴兵, 袁银男, 梅德清, 江俊康, 戴珊珊. 椭球模型下通过雾场的多重光散射谱. , 2012, 61(8): 084201. doi: 10.7498/aps.61.084201
[12]	杨春, 冯玉芳, 余毅. 动力学研究AlN/α-Al2Ｏ3（0001）薄膜生长初期的吸附与扩散. , 2009, 58(5): 3553-3559. doi: 10.7498/aps.58.3553
[13]	李美丽, 张迪, 孙宏宁, 付兴烨, 姚秀伟, 李丛, 段永平, 闫元, 牟洪臣, 孙民华. 二元Lennard-Jones液体的相分离过程及其扩散性质的分子动力学研究. , 2008, 57(11): 7157-7163. doi: 10.7498/aps.57.7157
[14]	王永亮, 张超, 唐鑫, 张庆瑜. 表面Cu原子间相互作用对Cu(001)表面跳跃扩散行为的影响. , 2006, 55(8): 4214-4220. doi: 10.7498/aps.55.4214
[15]	唐鑫, 张超, 张庆瑜. Cu(111)三维表面岛对表面原子扩散影响的分子动力学研究. , 2005, 54(12): 5797-5803. doi: 10.7498/aps.54.5797
[16]	王秀英, 高明, 孙力玲, 刘日平, 张君, 王文魁. 注入Mo 在Zr57Nb5Cu15.4Ni12.6Al10非晶合金中的扩散. , 2004, 53(1): 200-203. doi: 10.7498/aps.53.200
[17]	王宏霞, 何晨. 细胞神经网络的动力学行为. , 2003, 52(10): 2409-2414. doi: 10.7498/aps.52.2409
[18]	金进生, 夏阿根, 叶高翔. 带电液体基底表面银原子的凝聚和扩散行为. , 2002, 51(9): 2144-2149. doi: 10.7498/aps.51.2144
[19]	胡晓君, 戴永兵, 何贤昶, 沈荷生, 李荣斌. 空位在金刚石近(001)表面扩散的分子动力学模拟. , 2002, 51(6): 1388-1392. doi: 10.7498/aps.51.1388
[20]	张海燕. 多分量胶体悬浮系统转动扩散张量的反射理论. , 2002, 51(2): 449-455. doi: 10.7498/aps.51.449

计量

文章访问数: 5523
PDF下载量: 90
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

椭球胶体在圆球胶体体系中扩散行为的实验研究