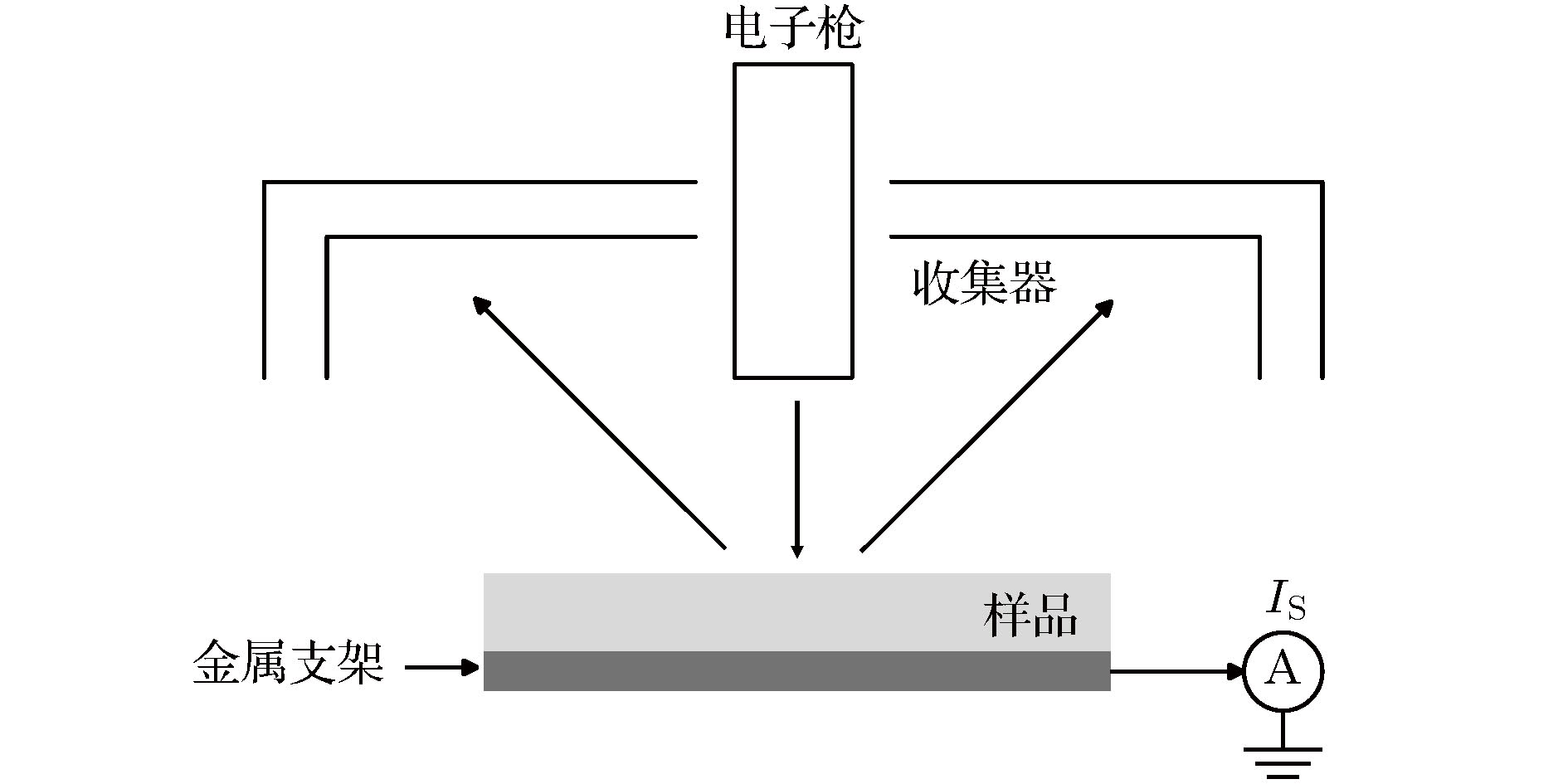
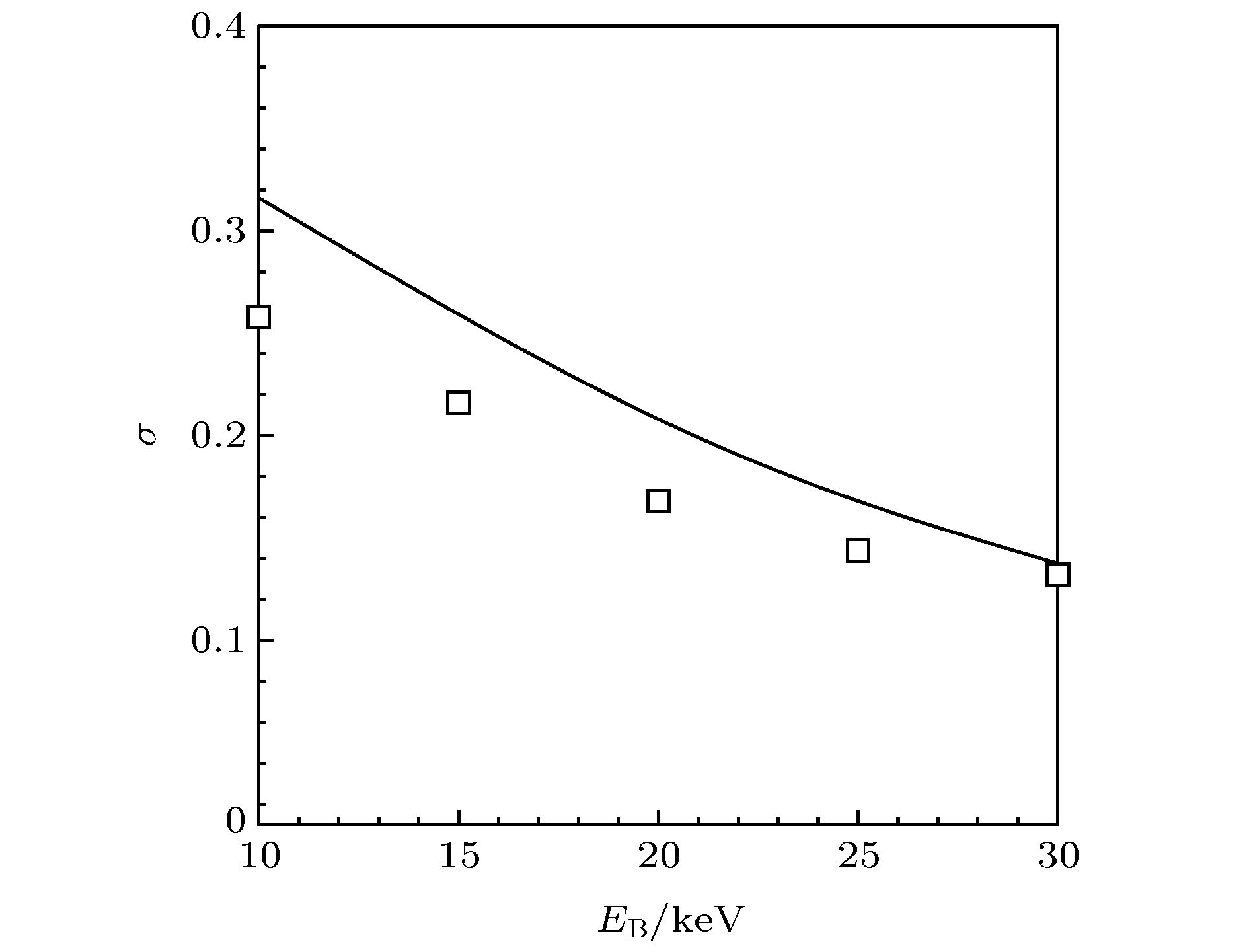
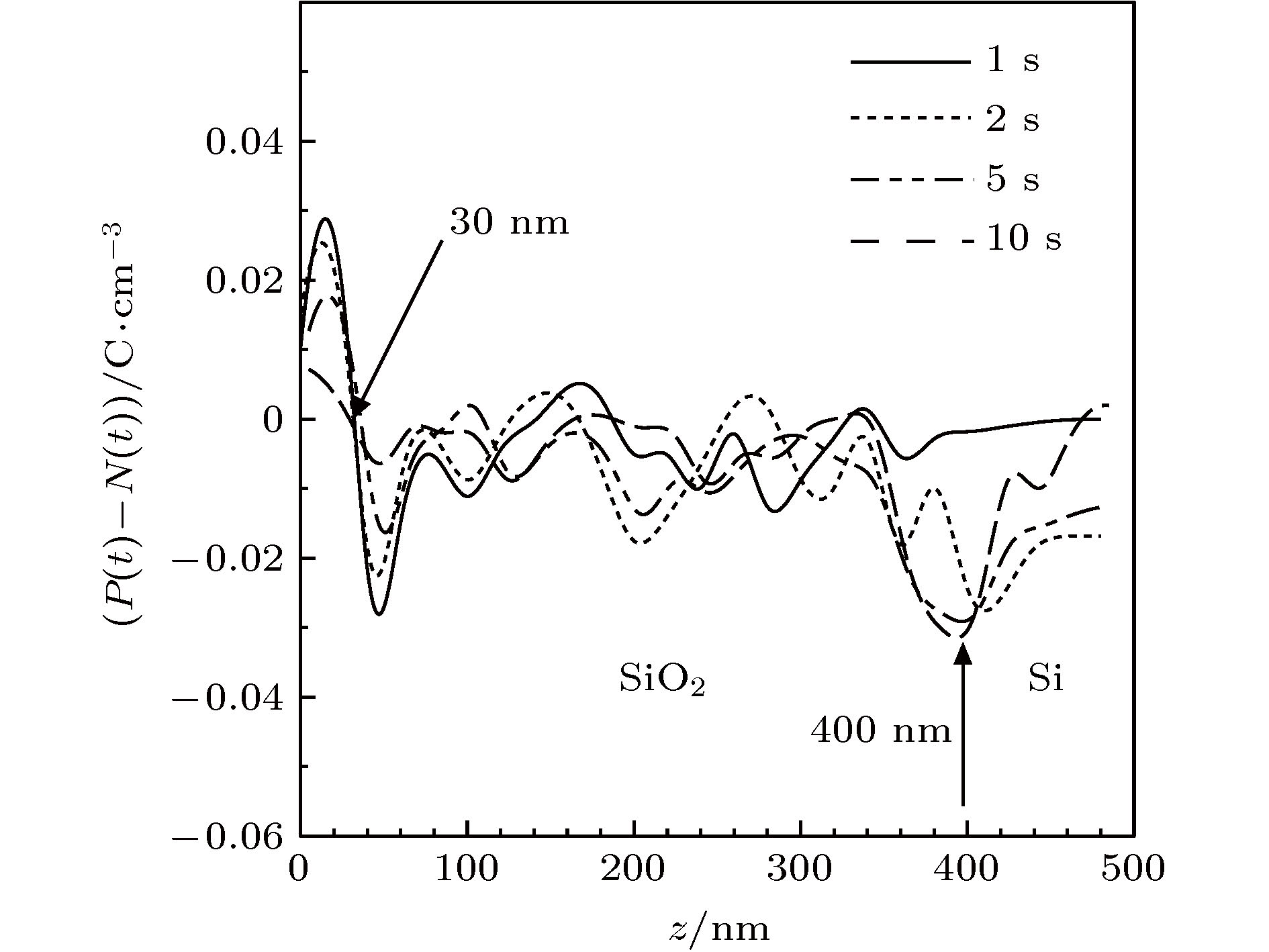
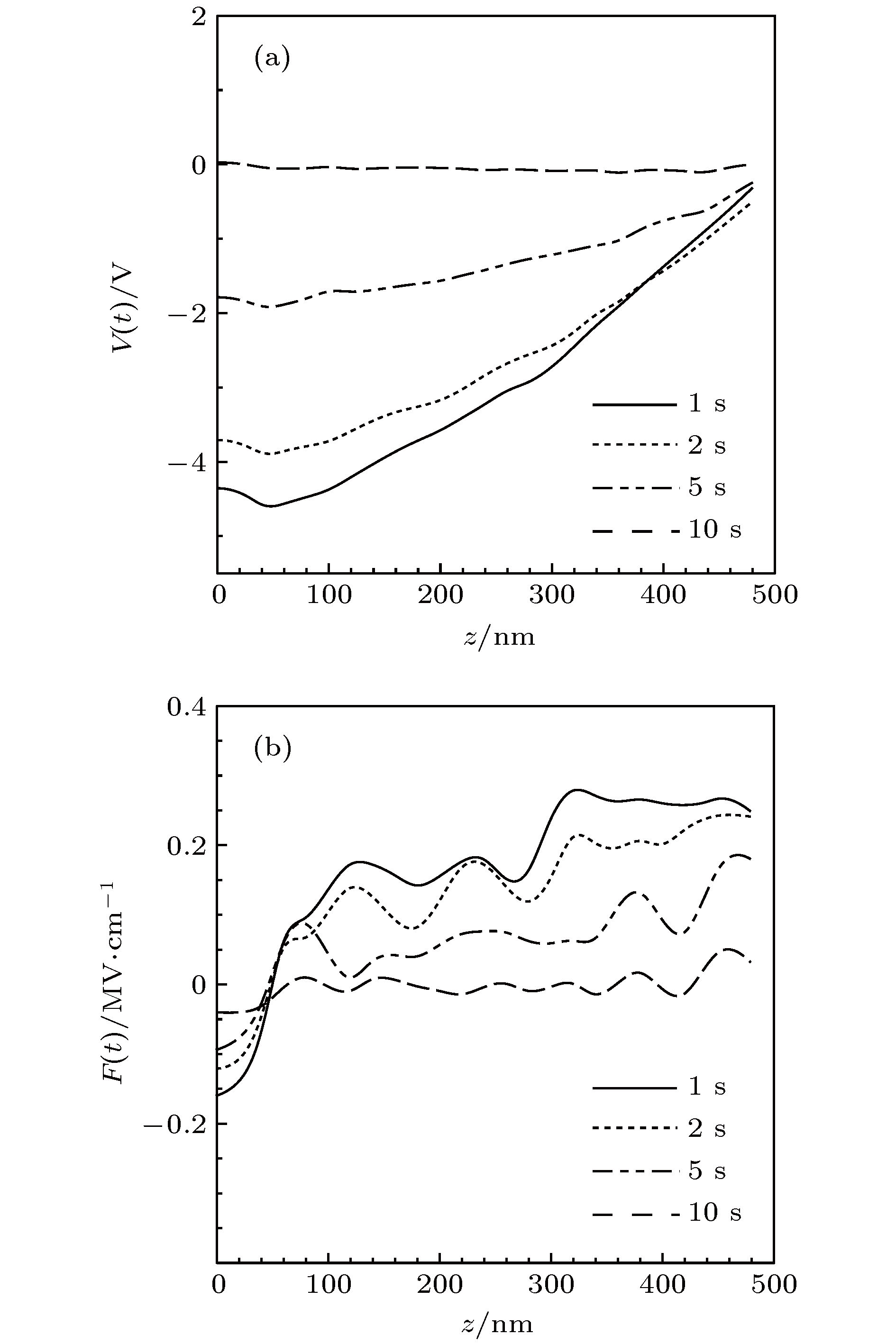
-
电子束照射下电介质/半导体样品的电子束感生电流(electron beam induced current, EBIC)是其电子显微检测的重要手段. 结合数值模拟和实验测量, 研究了高能电子束辐照下SiO2/Si薄膜的瞬态EBIC特性. 基于Rutherford模型和快二次电子模型研究电子的散射过程, 基于电流连续性方程计算电荷的输运、俘获和复合过程, 获得了电荷分布、EBIC和透射电流瞬态特性以及束能和束流对它们的影响. 结果表明, 由于电子散射效应, 自由电子密度沿入射方向逐渐减小. 由于二次电子出射, 净电荷密度呈现近表面为正、内部为负的特性, 空间电场在表面附近为正而在样品内部为负, 导致一些电子输运到基底以及一些出射二次电子返回表面. SiO2与Si界面处俘获电子导致界面附近负电荷密度高于周围区域. 随电子束照射样品内部净电荷密度逐渐降低, 带电强度减弱. 同时, 负电荷逐渐向基底输运, EBIC和样品电流逐渐增大, 电场强度逐渐减小. 由于样品带电强度较弱, 表面出射电流和透射电流随照射基本保持恒定. EBIC、透射电流及表面出射电流均随束流呈现近似正比例关系. 对于本文SiO2/Si薄膜, 透射电流随束能的升高逐渐增大并接近于束流值, EBIC在束能约15 keV时呈现极大值.The electron beam induced current (EBIC) characteristics of dielectric/semiconductor thin films under the electron beam (e-beam) irradiation is the important means of implementing the electron microscopic detection. The transient EBIC characteristics of the SiO2/Si thin film irradiated by a high-energy e-beam are investigated by combining the numerical simulation and the experimental measurement. The scattering process of electrons is simulated by the Rutherford scattering model and the fast secondary electron model, and the charge transport, trapping and the recombination process are calculated by the current continuity equation and the Poisson equation. The transient charge distribution, EBIC and the transmission current are obtained, and influence of the beam current and the beam energy on them are analyzed. The results show that due to the electron scattering effect, the free electron density decreases gradually along the incident direction. The net charge density near the surface is positive and negative along the incident direction because of secondary electrons (SEs) emitted from the surface, and therefore the electric field intensity is positive near the surface and negative inside sample, which causes some electrons to be transported to the substrate and some SEs return to the surface. The negative charge density at the SiO2/Si interface is higher than that in the nearby region because some electrons are trapped by the interface trap. With the decrease of the net charge density with e-beam irradiation, the charging intensity decreases gradually. Meanwhile, electrons are gradually transported to the substrate, and consequently EBIC and the sample current increase and the electric field intensity decreases with e-beam irradiation. However, due to the weak charging intensity, the surface emission current and the transmission current remain almost invariant with e-beam irradiation. The EBIC, the transmission current and the surface emission current are approximately proportional to the beam current. For the SiO2/Si thin film in this work, the transmission current increases gradually to the beam current value with the increase of the beam energy, and the EBIC presents a maximum value at the beam energy of about 15 keV.
-
Keywords:
- numerical simulation /
- electron beam induced current /
- trapping /
- transport
[1] Zhang M, Wang X X, Cao W Q, Yuan J, Cao M S 2019 Adv. Opt. Mater. 7 1900689
Google Scholar
[2] Cao M S, Wang X X, Zhang M, Shu J C, Cao W Q, Yang H J, Fang X Y, Yuan J 2019 Adv. Funct. Mater. 29 1807398
Google Scholar
[3] Ben Ammar L, Fakhfakh S, Jbara O, Rondot S 2017 J. Microsc. 265 322
Google Scholar
[4] Cazaux J 2010 J. Electron. Spectrosc. Relat. Phenom. 176 58
Google Scholar
[5] Bai M, Pease F 2004 J. Vac. Sci. Technol. B 22 2907
Google Scholar
[6] Ben Ammar L, Fakhfakh S, Jbara O, Rondot S, Hadjadj A 2017 Micron 98 39
Google Scholar
[7] Wong W K, Rau E I, Thong J T L 2004 Ultramicroscopy 101 183
Google Scholar
[8] Zhang H B, Li W Q, Wu D W 2009 J. Electron Microsc. 58 15
[9] Hoskins B D, Adam G C, Strelcov E, Zhitenev N, Kolmakov A, Strukov D B, McClelland J J 2017 Nat. Commun. 8 1972
Google Scholar
[10] Fitting H J, Touzin M 2011 J. Appl. Phys. 110 044111
Google Scholar
[11] 孙祥乐, 高思伟, 毛渲, 龚晓霞, 余黎静, 宋欣波, 柴圆媛, 尚发兰, 信思树, 太云见 2019 红外技术 41 742
Sun X L, Gao S W, Mao X, Gong X X, Yu L J, Song X B, Chai Y Y, Shang F L, Xin S S, Tai Y J 2019 Infrared Technology 41 742
[12] Fakhfakh S, Jbara O, Rondot S, Hadjadj A, Fakhfakh Z 2012 J. Non-Cryst Solids 358 1157
Google Scholar
[13] 封国宝, 曹猛, 崔万照, 李军, 刘纯亮, 王芳 2017 66 067901
Google Scholar
Feng G B, Cao M, Cui W Z, Li J, Liu C L, Wang F 2017 Acta Phys. Sin. 66 067901
Google Scholar
[14] 李维勤, 郝杰, 张海波 2015 64 086801
Google Scholar
Li W Q, Hao J, Zhang H B 2015 Acta Phys. Sin. 64 086801
Google Scholar
[15] 白春江, 封国宝, 崔万照, 贺永宁, 张雯, 胡少光, 叶鸣, 胡天存, 黄光荪, 王琪 2018 67 037902
Google Scholar
Bai C J, Feng G B, Cui W Z, He Y N, Zhang W, Hu S G, Ye M, Hu T C, Huang G S, Wang Q 2018 Acta Phys. Sin. 67 037902
Google Scholar
[16] Cornet N, Goeuriot D, Guerret-Piécourt C, Juvé D, Tréheux D, Touzin M, Fitting H J 2008 J. Appl. Phys. 103 064110
Google Scholar
[17] Cazaux J 2012 J. Electron Microsc. 61 261
Google Scholar
[18] Li W Q, Mu K, Xia R H 2011 Micron 42 443
Google Scholar
[19] 李维勤, 刘丁, 张海波 2014 63 227303
Google Scholar
Li W Q, Liu D, Zhang H B 2014 Acta Phys. Sin. 63 227303
Google Scholar
[20] 翁明, 胡天存, 曹猛, 徐伟军 2015 64 157901
Google Scholar
Weng M, Hu T C, Cao M, Xu W J 2015 Acta Phys. Sin. 64 157901
Google Scholar
[21] Joy D C 1995 Monte Carlo Modeling for Electron Microscopy and Microanalysis (New York: Oxford University Press) p27
[22] Touzin M, Goeuriot D, Guerret-Piécourt C, Juvé D, Tréheux D, Fitting H J 2006 J. Appl. Phys. 99 114110
Google Scholar
[23] Cao M S, Shu J C, Wang X X, Wang X, Zhang M, Yang H J, Fang X, Yuan J 2019 Ann. Phys. 531 1800390
Google Scholar
[24] Buchanan D A, Fischetti M V, Dimaria D J 1991 Phys. Rev. B 43 1471
Google Scholar
[25] Gushterov A, Simeonov S 2004 Vacuum 76 315
Google Scholar
[26] Rau E I 2008 Appl. Surf. Sci. 254 2110
Google Scholar
-
图 1 电子束与样品相互作用产生的各类电流示意图
Fig. 1. Schematic of currents generated by the interaction of e-beams with samples.
图 3 电子总产额的模拟(直线)和实验(方块)结果
Fig. 3. Simulated (lines) and experimental (squares) results of total electron yield.
图 4 自由电子密度N(t)沿入射方向分布
Fig. 4. Simulated free charge densities N(t) along the incident direction.
图 5 净电荷密度(P(t) – N(t))沿入射方向分布
Fig. 5. Simulated net space densities (P(t) – N(t)) along the incident direction.
图 6 (a)空间电位V(t)和(b)空间电场F(t)沿入射方向分布模拟结果
Fig. 6. Simulated (a) space potentials V(t) and (b) space fields F(t) along the incident direction.
图 7 有效出射电流II的模拟(直线)和测量(方块)结果
Fig. 7. Simulated (line) and experimental (squares) effective emission currents II.
图 8 (a) IEBIC及ITE的模拟结果; (b) IS的模拟(直线)和测量(方块)结果
Fig. 8. (a) Simulated IEBIC and ITE; (b) simulated (line) and experimental (squares) IS.
图 9 模拟得到的不同束流时电子束感生电流IEBIC的稳态结果
Fig. 9. Simulated IEBIC in the steady state under the different values of beam current IB.
图 10 模拟得到的不同束能时透射电流ITE的时变特性
Fig. 10. Simulated ITE as a function of the irradiation time in the different beam energies EB.
图 11 模拟得到的不同束能时IEBIC的时变特性
Fig. 11. Simulated IEBIC as a function of the irradiation time in the different beam energies EB.
表 1 电子散射过程参数默认设置
Table 1. Default values of parameters in the scattering process.
参数 SiO2 Si ρ/g·cm–3 2.26 2.32 $\bar A $/g·mole–1 20 28.1 $\bar J $/keV 0.139 0.173 $\bar Z $ 10 14 
下载: 导出CSV
表 2 实验参数默认设置
Table 2. Default values of parameters.
束能EB/keV 束流IB/nA 扫描区域/mm2 扫描周期/s 10, 15, 20, 30 1.6 1 × 1 1.2
下载: 导出CSV
表 3 数值计算参数默认设置
Table 3. Default values of parameters.
参数 取值 束能EB/keV 10 束流IB/nA 1.6 体缺陷密度/cm–3 1017 界面俘获密度/cm–2 1014
下载: 导出CSV
-
[1] Zhang M, Wang X X, Cao W Q, Yuan J, Cao M S 2019 Adv. Opt. Mater. 7 1900689
Google Scholar
[2] Cao M S, Wang X X, Zhang M, Shu J C, Cao W Q, Yang H J, Fang X Y, Yuan J 2019 Adv. Funct. Mater. 29 1807398
Google Scholar
[3] Ben Ammar L, Fakhfakh S, Jbara O, Rondot S 2017 J. Microsc. 265 322
Google Scholar
[4] Cazaux J 2010 J. Electron. Spectrosc. Relat. Phenom. 176 58
Google Scholar
[5] Bai M, Pease F 2004 J. Vac. Sci. Technol. B 22 2907
Google Scholar
[6] Ben Ammar L, Fakhfakh S, Jbara O, Rondot S, Hadjadj A 2017 Micron 98 39
Google Scholar
[7] Wong W K, Rau E I, Thong J T L 2004 Ultramicroscopy 101 183
Google Scholar
[8] Zhang H B, Li W Q, Wu D W 2009 J. Electron Microsc. 58 15
[9] Hoskins B D, Adam G C, Strelcov E, Zhitenev N, Kolmakov A, Strukov D B, McClelland J J 2017 Nat. Commun. 8 1972
Google Scholar
[10] Fitting H J, Touzin M 2011 J. Appl. Phys. 110 044111
Google Scholar
[11] 孙祥乐, 高思伟, 毛渲, 龚晓霞, 余黎静, 宋欣波, 柴圆媛, 尚发兰, 信思树, 太云见 2019 红外技术 41 742
Sun X L, Gao S W, Mao X, Gong X X, Yu L J, Song X B, Chai Y Y, Shang F L, Xin S S, Tai Y J 2019 Infrared Technology 41 742
[12] Fakhfakh S, Jbara O, Rondot S, Hadjadj A, Fakhfakh Z 2012 J. Non-Cryst Solids 358 1157
Google Scholar
[13] 封国宝, 曹猛, 崔万照, 李军, 刘纯亮, 王芳 2017 66 067901
Google Scholar
Feng G B, Cao M, Cui W Z, Li J, Liu C L, Wang F 2017 Acta Phys. Sin. 66 067901
Google Scholar
[14] 李维勤, 郝杰, 张海波 2015 64 086801
Google Scholar
Li W Q, Hao J, Zhang H B 2015 Acta Phys. Sin. 64 086801
Google Scholar
[15] 白春江, 封国宝, 崔万照, 贺永宁, 张雯, 胡少光, 叶鸣, 胡天存, 黄光荪, 王琪 2018 67 037902
Google Scholar
Bai C J, Feng G B, Cui W Z, He Y N, Zhang W, Hu S G, Ye M, Hu T C, Huang G S, Wang Q 2018 Acta Phys. Sin. 67 037902
Google Scholar
[16] Cornet N, Goeuriot D, Guerret-Piécourt C, Juvé D, Tréheux D, Touzin M, Fitting H J 2008 J. Appl. Phys. 103 064110
Google Scholar
[17] Cazaux J 2012 J. Electron Microsc. 61 261
Google Scholar
[18] Li W Q, Mu K, Xia R H 2011 Micron 42 443
Google Scholar
[19] 李维勤, 刘丁, 张海波 2014 63 227303
Google Scholar
Li W Q, Liu D, Zhang H B 2014 Acta Phys. Sin. 63 227303
Google Scholar
[20] 翁明, 胡天存, 曹猛, 徐伟军 2015 64 157901
Google Scholar
Weng M, Hu T C, Cao M, Xu W J 2015 Acta Phys. Sin. 64 157901
Google Scholar
[21] Joy D C 1995 Monte Carlo Modeling for Electron Microscopy and Microanalysis (New York: Oxford University Press) p27
[22] Touzin M, Goeuriot D, Guerret-Piécourt C, Juvé D, Tréheux D, Fitting H J 2006 J. Appl. Phys. 99 114110
Google Scholar
[23] Cao M S, Shu J C, Wang X X, Wang X, Zhang M, Yang H J, Fang X, Yuan J 2019 Ann. Phys. 531 1800390
Google Scholar
[24] Buchanan D A, Fischetti M V, Dimaria D J 1991 Phys. Rev. B 43 1471
Google Scholar
[25] Gushterov A, Simeonov S 2004 Vacuum 76 315
Google Scholar
[26] Rau E I 2008 Appl. Surf. Sci. 254 2110
Google Scholar
下载:
计量
- 文章访问数: 8357
- PDF下载量: 116
- 被引次数: 0
