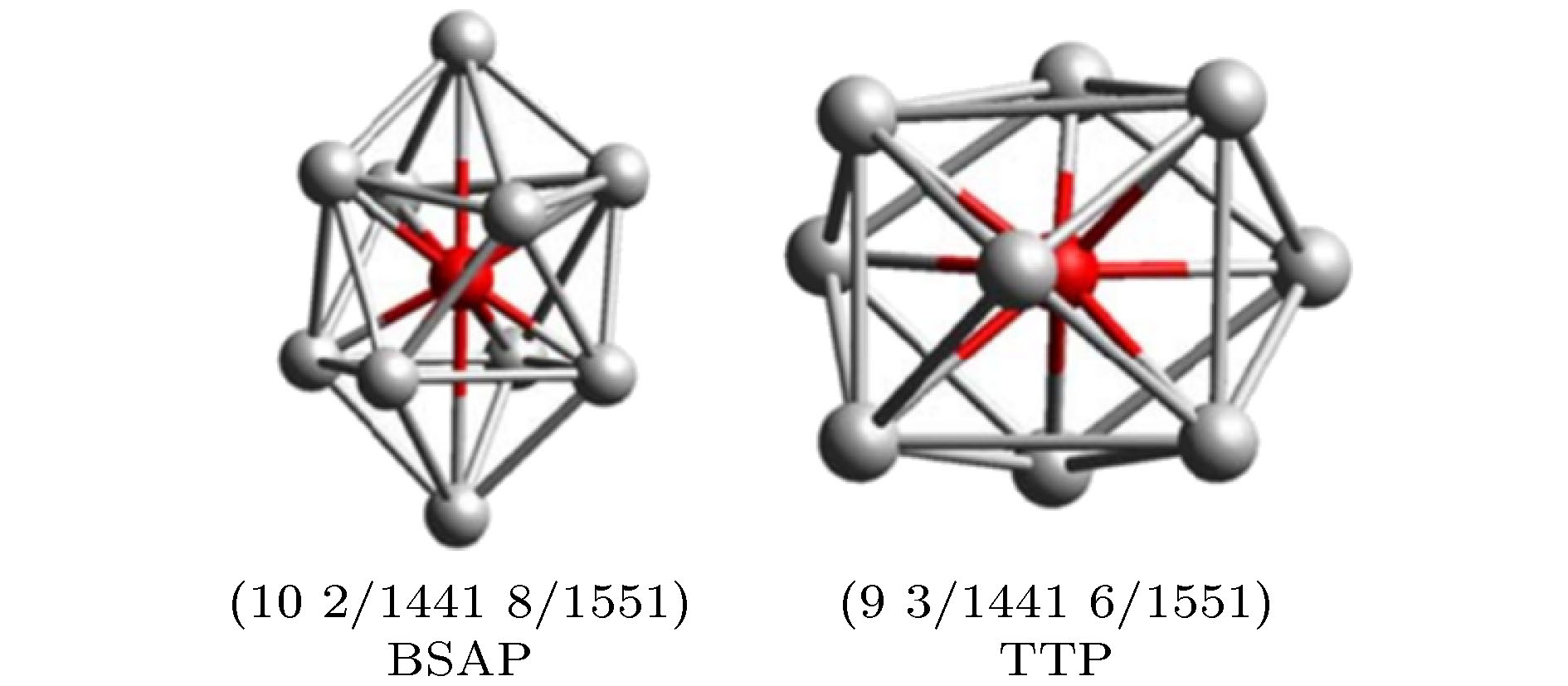
-
采用分子动力学(MD)模拟计算, 对Pd82Si18合金快凝过程中基本原子团簇的遗传特性、演化趋势和结构稳定性进行了研究. 团簇类型指数法(CTIM)分析表明: 非晶固体中Si原子为中心的(10 2/1441 8/1551)双帽阿基米德反棱柱(BSAP)团簇数目占据优势. 快凝过程中, BSAP结构团簇具有最大的遗传分数, 并且其他以Si原子为中心的Kasper团簇大多都会向BSAP结构团簇转变. 通过对Si原子为中心的Kasper基本团簇电子性质第一性原理计算发现, 体系中BSAP团簇的结合能最低, 结构稳定性较高, 与分子动力学计算结果一致.
-
关键词:
- Pd82Si18合金 /
- 快速凝固 /
- 团簇 /
- 遗传 /
- 电子性质
Molecular dynamics (MD) simulation and first-principles calculation were used to study the heredity characteristics, evolution trend and structural stability of basic clusters during the rapid solidification of Pd82Si18 alloy. The local atomic structures were characterized by the pair distribution function g(r) and the extended cluster-type index method (CTIM). The MD simulations reveal that the number of bi-cap Archimedes anti-prism (BSAP) clusters with CTIM index (10 2/1441 8/1551) is dominant in the amorphous solids rather than three-cap triangular prism(TTP) with CTIM index (9 3/1441 6/1551), which is identified be the most popular basic units in Pd82Si18 alloys analyzed by Voronoi index Relative to other basic clusters, the Si-centered BSAP possesses much larger fraction in the glassy state of Pd82Si18 alloys. Different from the findings in Cu-Zr alloys, the Si-centered BSAP instead of icosahedra has a larger hereditary fraction than any other Kasper clusters. During the solidification, it was found that most of the other Si-centered basic clusters are transferred into BSAP. Via the DFT calculations, it is observed that the Si-centered basic clusters with higher fraction of heredity and possesses lower binding energy. Among of them, BSAP always keeps lower binding energy than any other Si-centered Kasper clusters during the rapid solidification, resulting in its highest structural stability and the largest heredity fraction.-
Keywords:
- Pd82Si18alloy /
- rapid solidification /
- cluster /
- heredity /
- electronic property
[1] Kui H W, Greer A L, Turnbull D 1984 Appl. Phys. Lett. 45 615
Google Scholar
[2] Inoue A 1997 Mater. Sci. Eng. A 226-228 357
[3] Nelson D 1983 Phys. Rev. B 28 5515
Google Scholar
[4] Sha Z D, Xu B, Shen L, Zhang A H, Feng Y P, Li Y 2010 J. Appl. Phys. 107 063508
Google Scholar
[5] Wen D D, Peng P, Jiang Y Q, Liu R S 2013 J. Non-Cryst. Solids 378 61
Google Scholar
[6] 邓永和, 文大东, 彭超, 韦彦丁, 赵瑞, 彭平 2016 65 066401
Google Scholar
Deng Y H, Wen D D, Peng C, Wei Y D, Zhao R, Peng P 2016 Acta Phys. Sin. 65 066401
Google Scholar
[7] Wu Z W, Li M Z, Wang W H, Liu K X 2013 Phys. Rev. B 88 054202
Google Scholar
[8] Cheng Y Q, Sheng H W, Ma E 2008 Phys. Rev. B 78 014207
Google Scholar
[9] Luo H B, Xiong L H, Ahmad A S, Li A G, Yang K, Glazyrin K, Liermann H P, Franz H, Wang X D, Cao Q P, Zhang D X, Jiang J Z 2014 Acta Mater. 81 420
Google Scholar
[10] Luo W K, Ma E 2008 J. Non-Cryst. Solids 354 945
Google Scholar
[11] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
Google Scholar
[12] 彭超, 李媛, 邓永和, 彭平 2017 金属学报 53 1659
Peng C, Li Y, Deng Y H, Peng P 2017 Acta Metal. Sin. 53 1659
[13] Deng Y H, Wen D D, Li Y, Liu J, Peng P 2018 Philos.Mag. 98 2861
Google Scholar
[14] 姚可夫, 陈娜 2008 中国科学 G 辑 38 387
Yao K F, Chen N 2008 Sci. China Ser. G 38 387
[15] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[16] https:\\www.google.com/site/eampotentials/Home/PdSi[2019-6-21]
[17] Delley B 2000 J. Chem. Phys. 113 7756
Google Scholar
[18] Delley B 1990 J. Chem. Phys. 92 508
Google Scholar
[19] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[20] Mattern N, Schops A, Kuhn U, Acker J, Eckert J 2008 J. Non-Cryst. Solids 354 1054
Google Scholar
[21] Honeycutt J D, Andersen H C 1987 J. Phys. Chem. 91 4950
Google Scholar
[22] 文大东, 彭平, 蒋元祺, 田泽安, 刘让苏 2013 62 196101
Wen D D, Peng P, Jiang Y Q, Tian Z A, Liu R S 2013 Acta Phys. Sin. 62 196101
[23] Tian Z A, Liu R S, Dong K J, Yu A B 2011 Euro. Phys. Lett. 96 36001
Google Scholar
[24] Wang H, Hu T, Qin J Y, Zhang T 2012 J. Appl. Phys. 112 073520
Google Scholar
[25] Cheng Y Q, Ding J, Ma E 2013 Mater. Res. Lett. 1 3
Google Scholar
[26] Jiang Y Q, Peng P, Wen D D, Han S C, Hou Z Y 2015 Comput. Mater. Sci. 99 156
Google Scholar
[27] Peng P, Li G F, Tian Z A, Dong K J, Liu R S 2009 Comput. Mater. Sci. 44 881
Google Scholar
-
图 1 Pd82Si18在1300 →300 K快凝过程中体系的双体分布函数(ΔT = 100 K) (a) g(r)tot; (b) g(r)tot的第一峰放大图; (c) g(r)tot第二峰放大图; (d) g(r)Pd-Si和g(r)Pd-Pd第一峰的放大图
Fig. 1. Pair distribution functions g(r) for rapidly solidified of Pd82Si18 from 1300 to 300 K (ΔT =100 K): (a) The g(r)tot curve; (b) first peak zoom of g(r)tot curve; (c) second peak zoom of g(r)tot curve; (d) first peak zoom of g(r)Pd-Si and g(r)Pd-Pd curve.
图 2 Pd82Si18合金在快凝过程中体系中原子的势能随温度的变化
Fig. 2. Average atomic potential energy of per atom in the simulated system as a function of temperature T during rapid solidification.
图 3 CTIM指数为(10 2/1441 8/1551)和(9 3/1441 6/1551)的BSAP和TTP的结构示意图(红色的球表示Si原子, 灰色球表示Pd原子)
Fig. 3. Schematic diagram of BSAP and TTP with CTIM index of (10 2/1441 8/1551) and (9 3/1441 6/1551) (Red ball denote Si atom and gray balls denote Pd atoms).
图 4 在快凝过程中Pd82Si18合金基本团簇的数量随温度的变化关系 (a)标准Kasper团簇; (b)变形的Kasper团簇
Fig. 4. The temperature dependence of the number of typical basic clusters in Pd82Si18 alloys: (a) Canonical Kasper clusters; (b) distorted Kasper clusters.
图 5 BSAP基本团簇遗传示意图 (a)完全遗传; (b)核遗传
Fig. 5. Basic cluster heredity schematic map of BSAP: (a) Perfect heredity; (b) core heredity
图 6 非晶合金Pd82Si18从810 K到300 K的遗传分数
Fig. 6. The heredity fractions in amorphous alloy Pd82Si18 from 810 K to 300 K.
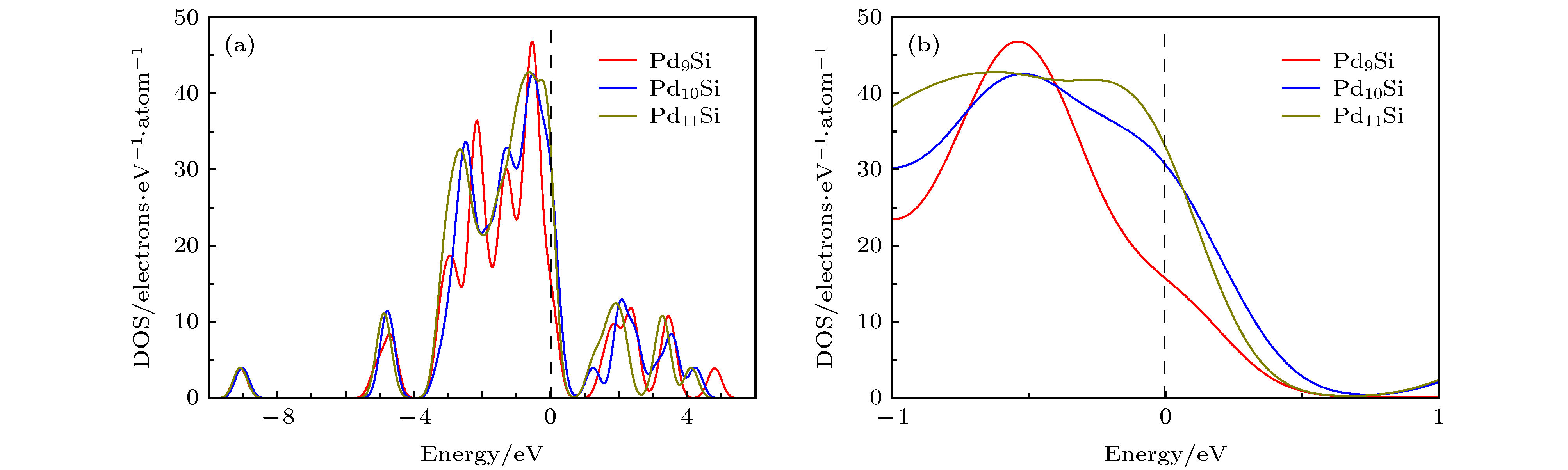
图 7 非晶合金Pd82Si18在810 K和300 K的几种基本Si为中心的团簇的结合能随团簇的分布 (a) 810 K基本Si为中心的团簇的结合能分布; (b) 300 K基本Si为中心的团簇的结合能分布; (c) 810 与300 K基本Si为中心的团簇的平均结合能分布
Fig. 7. Binding energies of several basic Si-centered clusters of amorphous alloy Pd82Si18 at 810 and 300 K depend on the distribution of clusters: (a) Binding energy distribution of basic Si-centered clusters at 800 K; (B) binding energy distribution of basic Si-centered clusters at 300 K; (c) distribution of average binding energy of basic Si-centered clusters at 800 and 300 K.
图 8 基本Si为中心的团簇优化后结构的结合能随团簇的分布 (a) EAM计算; (b)第一性原理计算
Fig. 8. Binding energies of several optimized basic Si-centered clusters depend on the distribution of clusters: (a) EAM calculations; (b) first-principle calculations.
图 9 局域电荷密度分布图 (a)Si原子为中心的Pd10Si团簇的局域电荷密度; (b)Si原子为中心的Pd9Si团簇的局域电子密度(图中白色和红色的字体表示切面上的原子)
Fig. 9. Pattern of local charge density distribution: (a) Local charge density of Si-centered Pd10Si cluster; (b) local charge density of Si-centered Pd9Si cluster(White and red fonts in the figure represents atoms on the tangent plane).
图 10 优化后基本Si原子为中心的团簇的态密度(DOS)图 (a) Pd9Si, Pd10Si与Pd11Si团簇的DOS图; (b) 图(a)中费米能级附近的放大图
Fig. 10. The density of states (DOS) diagrams of optimized basic Si-centered clusters: (a) The DOS of Pd9Si、Pd10Si and Pd11Si clusters; (b) zoom of the Fermi level in (a) diagram.
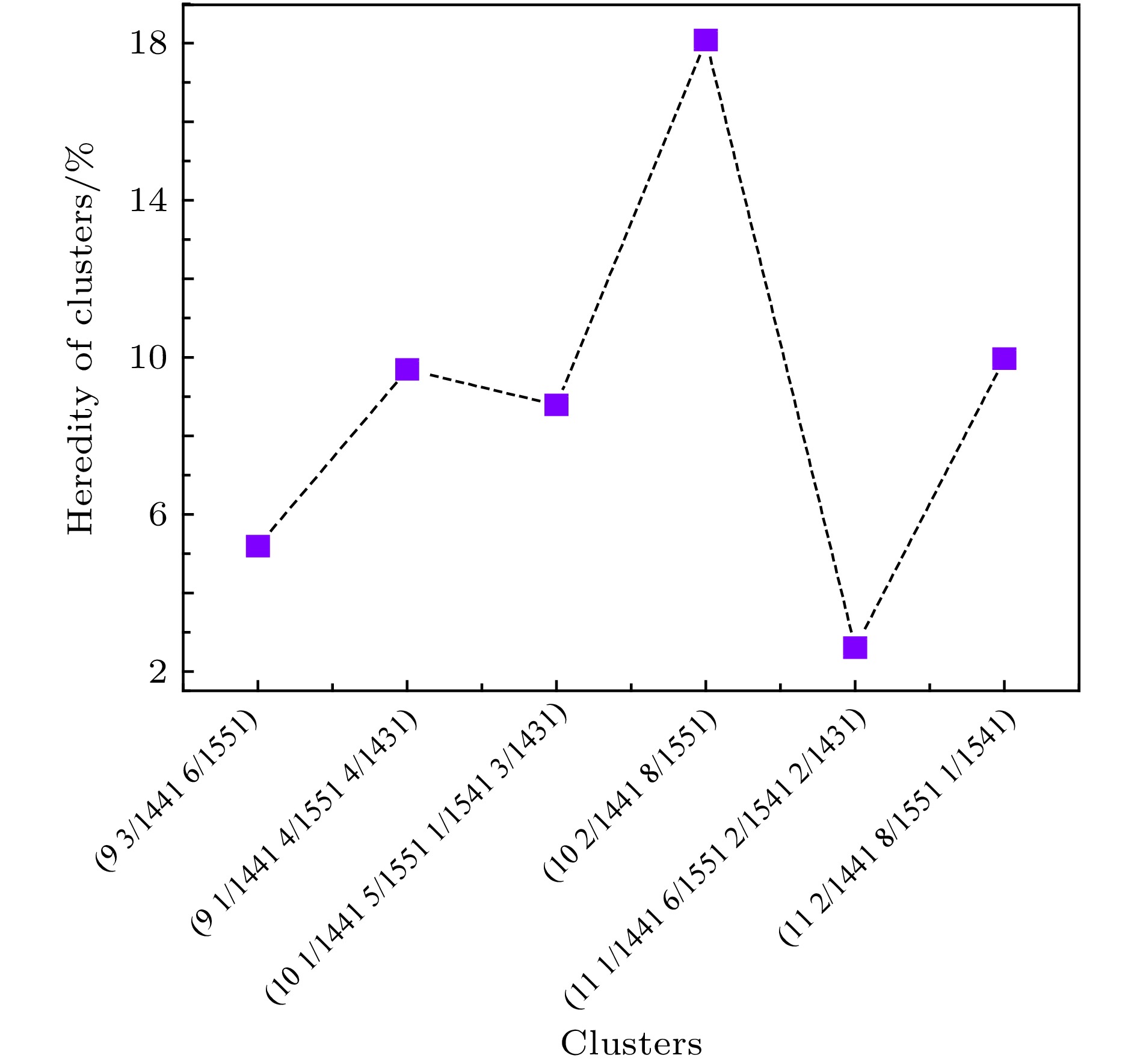
表 1 Pd82Si18合金从810 到300 K的几种基本Si原子为中心的团簇的演化分数
Table 1. The evolution fractions of several basic Si-centered clusters in amorphous alloy Pd82Si18 from 810 to 300 K.
810 K 300 K (9 3/1441 6/1551) (9 1/1441 4/1551 4/1431) (10 2/1441 8/1551) (10 1/1441 5/1551 1/1541 3/1431) (11 1/1441 6/1551 2/1541 2/1431) (11 2/1441 8/1551 1/1661) Sum/% (9 3/1441 6/1551) — 6.93 10.39 9.52 2.16 9.96 38.96 (9 1/1441 4/1551 4/1431) 7.75 — 16.67 7.36 3.10 9.69 44.57 (10 2/1441 8/1551) 5.80 6.97 — 10.12 1.49 12.94 37.32 (10 1/1441 5/1551 1/1541 3/1431) 5.71 5.93 14.73 — 2.42 9.67 38.46 (11 1/1441 6/1551 2/1541 2/1431) 6.49 4.55 13.64 10.39 — 11.04 46.11 (11 2/1441 8/1551 1/1661) 4.77 4.56 17.01 10.58 3.11 — 40.03 Sum(%) 30.52 28.94 72.44 47.97 12.28 53.30 — 
下载: 导出CSV
-
[1] Kui H W, Greer A L, Turnbull D 1984 Appl. Phys. Lett. 45 615
Google Scholar
[2] Inoue A 1997 Mater. Sci. Eng. A 226-228 357
[3] Nelson D 1983 Phys. Rev. B 28 5515
Google Scholar
[4] Sha Z D, Xu B, Shen L, Zhang A H, Feng Y P, Li Y 2010 J. Appl. Phys. 107 063508
Google Scholar
[5] Wen D D, Peng P, Jiang Y Q, Liu R S 2013 J. Non-Cryst. Solids 378 61
Google Scholar
[6] 邓永和, 文大东, 彭超, 韦彦丁, 赵瑞, 彭平 2016 65 066401
Google Scholar
Deng Y H, Wen D D, Peng C, Wei Y D, Zhao R, Peng P 2016 Acta Phys. Sin. 65 066401
Google Scholar
[7] Wu Z W, Li M Z, Wang W H, Liu K X 2013 Phys. Rev. B 88 054202
Google Scholar
[8] Cheng Y Q, Sheng H W, Ma E 2008 Phys. Rev. B 78 014207
Google Scholar
[9] Luo H B, Xiong L H, Ahmad A S, Li A G, Yang K, Glazyrin K, Liermann H P, Franz H, Wang X D, Cao Q P, Zhang D X, Jiang J Z 2014 Acta Mater. 81 420
Google Scholar
[10] Luo W K, Ma E 2008 J. Non-Cryst. Solids 354 945
Google Scholar
[11] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
Google Scholar
[12] 彭超, 李媛, 邓永和, 彭平 2017 金属学报 53 1659
Peng C, Li Y, Deng Y H, Peng P 2017 Acta Metal. Sin. 53 1659
[13] Deng Y H, Wen D D, Li Y, Liu J, Peng P 2018 Philos.Mag. 98 2861
Google Scholar
[14] 姚可夫, 陈娜 2008 中国科学 G 辑 38 387
Yao K F, Chen N 2008 Sci. China Ser. G 38 387
[15] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[16] https:\\www.google.com/site/eampotentials/Home/PdSi[2019-6-21]
[17] Delley B 2000 J. Chem. Phys. 113 7756
Google Scholar
[18] Delley B 1990 J. Chem. Phys. 92 508
Google Scholar
[19] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[20] Mattern N, Schops A, Kuhn U, Acker J, Eckert J 2008 J. Non-Cryst. Solids 354 1054
Google Scholar
[21] Honeycutt J D, Andersen H C 1987 J. Phys. Chem. 91 4950
Google Scholar
[22] 文大东, 彭平, 蒋元祺, 田泽安, 刘让苏 2013 62 196101
Wen D D, Peng P, Jiang Y Q, Tian Z A, Liu R S 2013 Acta Phys. Sin. 62 196101
[23] Tian Z A, Liu R S, Dong K J, Yu A B 2011 Euro. Phys. Lett. 96 36001
Google Scholar
[24] Wang H, Hu T, Qin J Y, Zhang T 2012 J. Appl. Phys. 112 073520
Google Scholar
[25] Cheng Y Q, Ding J, Ma E 2013 Mater. Res. Lett. 1 3
Google Scholar
[26] Jiang Y Q, Peng P, Wen D D, Han S C, Hou Z Y 2015 Comput. Mater. Sci. 99 156
Google Scholar
[27] Peng P, Li G F, Tian Z A, Dong K J, Liu R S 2009 Comput. Mater. Sci. 44 881
Google Scholar
下载:
计量
- 文章访问数: 6906
- PDF下载量: 87
- 被引次数: 0
