-
Reference-frame-independent measurement-device-independent quantum key distribution is adopted to avoid aligning the reference frames in realistic setup, which can guarantee the system security against the slow drift of reference frame. However, the relative motion of reference frame including deviation and fluctuation can influence the performance of reference-frame-independent measurement-device-independent quantum key distribution in practical experimental demonstration. In this paper, taking finite effect into consideration, the performance of reference-frame-independent measurement-device-independent quantum key distribution with biased bases under reference frame deviation and fluctuation is presented to evaluate the effect of the relative motion of reference frame on our scheme, which makes the analysis conform to reality. Our simulation results imply that the key rates fluctuate periodically with the reference frame rotating, while declining with the reference frame fluctuation increasing.
-
Keywords:
- quantum cryptography /
- quantum key distribution /
- reference frame independent /
- measurement device independent
[1] Shannon C E 1949 Bell Sys. Tech. J. 28 656
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[3] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[4] Stucki D, Walenta N, Vannel F, Thew R T, Gisin N, Zbinden H, Gray S, Towery C R, Ten S 2009 New J. Phys. 11 075003
Google Scholar
[5] Wang S, Chen W, Guo J F, Yin Z Q, Li H W, Zhou Z, Guo G C, Han Z F 2012 Opt. Lett. 37 1008
Google Scholar
[6] Wang S, Yin Z Q, Chen W, He D Y, Song X T, Li H W, Zhang L J, Zhou Z, Guo G C, Han Z F 2015 Nat. Photon. 9 832
Google Scholar
[7] Tang G Z, Sun S H, Li C Y 2019 Chin. Phys. Lett. 36 070301
Google Scholar
[8] Wang X Y, Zhao S H, Dong C, Zhu Z D, Gu W Y 2019 Quantum Inf. Process. 18 304
Google Scholar
[9] Liu H W, Qu W X, Dou T Q, Wang J P, Zhang Y, Ma H Q 2018 Chin. Phys. B 27 100309
Google Scholar
[10] Liu K, Li J, Zhu J R, Zhang C M, Wang Q 2017 Chin. Phys. B 26 120302
Google Scholar
[11] Gan Y H, Wang Y, Bao W S, He R S, Zhou C, Jiang M S 2019 Chin. Phys. Lett. 36 040301
Google Scholar
[12] Du G H, Li H W, Wang Y, Bao W S 2019 Chin. Phys. B 28 090301
Google Scholar
[13] Brassard G, Lütkenhaus N, Mor T, Sanders B C 2000 Phys. Rev. Lett. 85 1330
Google Scholar
[14] 陈艳辉, 王金东, 杜聪 2019 68 130301
Google Scholar
Chen Y H, Wang J D, Du C 2019 Acta Phys. Sin. 68 130301
Google Scholar
[15] 沈咏, 邹宏新 2010 59 1473
Google Scholar
Shen Y, Zou Y X 2010 Acta Phys. Sin. 59 1473
Google Scholar
[16] Huang J Z, Yin Z Q, Wang S, Li H W, Chen W, Han Z F 2012 Eur. Phys. J. D 66 159
Google Scholar
[17] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[18] Silva T F D, Vitoreti D, Xavier G B, Temporão G P, von der Weid J P 2013 Phys. Rev. A 88 052303
Google Scholar
[19] Tang Z Y, Liao Z F, Xu F H, Qi B, Qian L, Lo H K 2014 Phys. Rev. Lett. 112 190503
Google Scholar
[20] Yin H L, Chen T Y, Yu Z W, Liu H, You L X, Zhou Y H, Chen S J, Mao Y Q, Huang M Q, Zhang W J, Chen H, Li M J, Nolan D, Zhou F, Jiang X, Wang Z, Zhang Q, Wang X B, Pan J W 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[21] Yin Z Q, Wang S, Chen W, Li H W, Guo G C, Han Z F 2014 Quantum Inf. Process. 13 1237
Google Scholar
[22] Wang C, Yin Z Q, Wang S, Chen W, Han Z F 2017 Optica 4 1016
Google Scholar
[23] Zhang C M, Zhu J R, Wang Q 2017 Phys. Rev. A 95 032309
Google Scholar
[24] Liu H W, Wang J P, Ma H Q, Sun S H 2018 Optica 5 902
Google Scholar
[25] Zhang H, Zhang C H, Zhang C M, Guo G C, Wang Q 2019 Quantum Inform. Process. 18 313
Google Scholar
[26] Xue Q Y, Jiao R Z 2019 JOSA B 36 476
Google Scholar
[27] Pramanik T, Park B K, Cho Y, Han S W, Kim Y S, Moon S 2017 Phys. Lett. A 381 2497
Google Scholar
[28] Yoon J, Pramanik T, Park B K, Han S W, Kim S, Kim Y S, Moon S 2019 Opt. Commun. 441 64
Google Scholar
[29] Zhang C M, Zhang J R, Wang Q 2017 J. Lightwave Technol. 35 4574
Google Scholar
-
图 1 Alice和Bob的三组共轭基的实际位置关系图
Fig. 1. Relationship among reference frames of Alice and Bob.
图 2 参考系偏移和波动下有偏基RFI-MDI-QKD协议的C值 (a) 参数C与偏移角
$\theta $ 的关系图; (b) 参数C与波动角$\delta $ 的关系图Fig. 2. Parameter C of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation: (a) The parameter C vs. the reference frame deviation
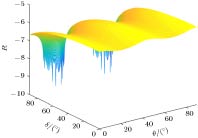
$\theta $ ; (b) the parameter C vs. the reference frame fluctuation$\delta $ .
图 3 有偏基RFI-MDI-QKD协议密钥率R与偏移角
$\theta $ 、波动角$\delta $ 的关系图Fig. 3. Secure key rates R of RFI-MDI-QKD with biased bases in regard to the reference frame deviation
$\theta $ and fluctuation$\delta $ .
图 4 参考系偏移和波动下有偏基RFI-MDI-QKD协议密钥率变化图 (a) 密钥率R与偏移角
$\theta $ 的关系图; (b) 协议密钥率R与波动角$\delta $ 的关系图Fig. 4. Secure key rates of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation: (a) The secure key rates R vs. the reference frame deviation
$\theta $ ; (b) the secure key rates R vs. the reference frame fluctuation$\delta $ .表 1 有偏基RFI-MDI-QKD协议的主要仿真参数
Table 1. List of parameters of RFI-MDI-QKD with biased bases in the simulation.
${Y_0}$ ed ${e_0}$ f ηd $1.2 \times {10^{-6}}$ 0.005 0.5 1.16 0.125 
下载: 导出CSV
-
[1] Shannon C E 1949 Bell Sys. Tech. J. 28 656
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[3] Lo H K, Ma X, Chen K 2005 Phys. Rev. Lett. 94 230504
Google Scholar
[4] Stucki D, Walenta N, Vannel F, Thew R T, Gisin N, Zbinden H, Gray S, Towery C R, Ten S 2009 New J. Phys. 11 075003
Google Scholar
[5] Wang S, Chen W, Guo J F, Yin Z Q, Li H W, Zhou Z, Guo G C, Han Z F 2012 Opt. Lett. 37 1008
Google Scholar
[6] Wang S, Yin Z Q, Chen W, He D Y, Song X T, Li H W, Zhang L J, Zhou Z, Guo G C, Han Z F 2015 Nat. Photon. 9 832
Google Scholar
[7] Tang G Z, Sun S H, Li C Y 2019 Chin. Phys. Lett. 36 070301
Google Scholar
[8] Wang X Y, Zhao S H, Dong C, Zhu Z D, Gu W Y 2019 Quantum Inf. Process. 18 304
Google Scholar
[9] Liu H W, Qu W X, Dou T Q, Wang J P, Zhang Y, Ma H Q 2018 Chin. Phys. B 27 100309
Google Scholar
[10] Liu K, Li J, Zhu J R, Zhang C M, Wang Q 2017 Chin. Phys. B 26 120302
Google Scholar
[11] Gan Y H, Wang Y, Bao W S, He R S, Zhou C, Jiang M S 2019 Chin. Phys. Lett. 36 040301
Google Scholar
[12] Du G H, Li H W, Wang Y, Bao W S 2019 Chin. Phys. B 28 090301
Google Scholar
[13] Brassard G, Lütkenhaus N, Mor T, Sanders B C 2000 Phys. Rev. Lett. 85 1330
Google Scholar
[14] 陈艳辉, 王金东, 杜聪 2019 68 130301
Google Scholar
Chen Y H, Wang J D, Du C 2019 Acta Phys. Sin. 68 130301
Google Scholar
[15] 沈咏, 邹宏新 2010 59 1473
Google Scholar
Shen Y, Zou Y X 2010 Acta Phys. Sin. 59 1473
Google Scholar
[16] Huang J Z, Yin Z Q, Wang S, Li H W, Chen W, Han Z F 2012 Eur. Phys. J. D 66 159
Google Scholar
[17] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[18] Silva T F D, Vitoreti D, Xavier G B, Temporão G P, von der Weid J P 2013 Phys. Rev. A 88 052303
Google Scholar
[19] Tang Z Y, Liao Z F, Xu F H, Qi B, Qian L, Lo H K 2014 Phys. Rev. Lett. 112 190503
Google Scholar
[20] Yin H L, Chen T Y, Yu Z W, Liu H, You L X, Zhou Y H, Chen S J, Mao Y Q, Huang M Q, Zhang W J, Chen H, Li M J, Nolan D, Zhou F, Jiang X, Wang Z, Zhang Q, Wang X B, Pan J W 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[21] Yin Z Q, Wang S, Chen W, Li H W, Guo G C, Han Z F 2014 Quantum Inf. Process. 13 1237
Google Scholar
[22] Wang C, Yin Z Q, Wang S, Chen W, Han Z F 2017 Optica 4 1016
Google Scholar
[23] Zhang C M, Zhu J R, Wang Q 2017 Phys. Rev. A 95 032309
Google Scholar
[24] Liu H W, Wang J P, Ma H Q, Sun S H 2018 Optica 5 902
Google Scholar
[25] Zhang H, Zhang C H, Zhang C M, Guo G C, Wang Q 2019 Quantum Inform. Process. 18 313
Google Scholar
[26] Xue Q Y, Jiao R Z 2019 JOSA B 36 476
Google Scholar
[27] Pramanik T, Park B K, Cho Y, Han S W, Kim Y S, Moon S 2017 Phys. Lett. A 381 2497
Google Scholar
[28] Yoon J, Pramanik T, Park B K, Han S W, Kim S, Kim Y S, Moon S 2019 Opt. Commun. 441 64
Google Scholar
[29] Zhang C M, Zhang J R, Wang Q 2017 J. Lightwave Technol. 35 4574
Google Scholar
下载:
计量
- 文章访问数: 7583
- PDF下载量: 88
- 被引次数: 0
