-
氢(H)同位素滞留问题是聚变堆第一壁材料设计的关键, 而深入理解H在缺陷(如空位)处的非均匀形核长大过程有助于揭示H起泡及滞留的机制. 针对第一壁材料钨(W)中空位捕获H及其解离的动力学过程开展研究, 通过耦合捕获和解离两过程, 构建新物理模型, 避免了原单一过程的物理模型需准确记录相应事件首次发生时间的不足, 另外新模型可同时提取解离系数和有效捕获半径等动力学参数. 通过分子动力学模拟发现新模型能较好地描述W中空位-H复合体对H捕获和解离的动力学过程, 根据空位-H复合体随时间的演化曲线, 提取了有效捕获半径和解离系数等动力学参数. 一方面能为动力学蒙特卡罗和速率理论等长时空尺度方法提供输入参数, 另一方面促进了分子动力学的发展, 进而实现了以较低计算资源获得更可靠的计算结果.Tungsten (W) alloys and W-based alloys are the primary candidate materials for plasma-facing components in future fusion reactors (e.g. ITER and CFETR). One of the critical issues still to be clarified in the design of the fusion reactor materials is the retention of hydrogen (H) isotopes in W, when the plasma-facing materials are supposed to sustain high-flux plasma and high-energy neutron. The dynamical behaviours of H in W with radiation defects (e.g. vacancy) are of serious concerns for understanding the mechanism of H capture, retention and permeation in W. In this work, a new model to extract the effective capture radius (ECR) and dissociation coefficient simultaneously is presented through coupling the trapping process and detrapping process of H in W vacancy. In the new model, the quantity ratio of vacancy to H atom in vacancy-H complex (VHx+1) in the molecular dynamics (MD) simulations is described as a function of time, while the exact occurrence time of corresponding event is not required. This new model, combined with extensive MD calculations, enables the simultaneous determining of the ECR and dissociation coefficient of H in W vacancy. It is found that the parameters are dependent not only on the event type but also on temperature. The dissociation energy of H from vacancy-H complex decreases gradually with the increase of the trapped number of H atoms in the vacancy-H complex. It is also found that the common assumption (i.e. the ECR is equal to one lattice constant and the pre-exponential factor is equal to 1013 s–1) in the long-term simulation methods (e.g. kinetic Monte Carlo and rate theory) is not always valid, since these calculated dynamical parameters are dispersive. The new model to obtain more reliable results with lower cost of computing resources can be easily extended into the other similar kinetic processes (e.g. H/He trapping and detrapping processes in other materials systems). These calculated dynamical parameters should be potentially helpful in supplying the initial input parameters for the long-term simulation methods.
-
Keywords:
- capture radius /
- dissociation coefficient /
- molecular dynamics /
- vacancy
[1] Lu G H, Zhou H B, Becquart C S 2014 Nucl. Fusion 54 086001
Google Scholar
[2] 李建刚, 宋云涛, 刘永, 汪小琳, 万元熙 2016 聚变工程试验堆装置主机设计 (北京: 科学出版社) 第250−252页
Li J G, Song Y T, Liu Y, Wang X L, Wan Y X 2016 Main Machine Design of Fusion Engineering Test Reactor (Beijing: Science Press) pp250−252 (in Chinese)
[3] Jia Y Z, Liu W, Xu B, Luo G N, Li C, Fu B Q, de Temmerman G 2015 J. Nucl. Mater. 463 312
Google Scholar
[4] Yi X, Jenkins M L, Hattar K, Edmondson P D, Roberts S G 2015 Acta Mater. 92 163
Google Scholar
[5] Hu X, Koyanagi T, Fukuda M, Kumar N A P K, Snead L L, Wirth B D, Katoh Y 2016 J. Nucl. Mater. 480 235
Google Scholar
[6] Fu B Q, Lai W S, Yuan Y, Xu H Y, Li C, Jia Y Z, Liu W 2013 Chinese Phys. B 22 126601
Google Scholar
[7] Ye M Y 2005 Plasma Sci. Technol. 7 2828
Google Scholar
[8] Fu B Q, Qiu M J, Zhai L, Yang A L, Hou Q 2019 Nucl. Instrum. Meth. B 450 220
Google Scholar
[9] Oyaidzu M, Hayashi T, Alimov V K 2016 Nucl. Mater. Energy 9 93
Google Scholar
[10] Jia Y Z, Liu W, Xu B, Qu S L, Shi L Q, Morgan T W 2017 Nucl. Fusion 57 034003
Google Scholar
[11] Heinola K, Ahlgren T 2010 Phys. Rev. B 81 073409
Google Scholar
[12] Frauenfelder R 1969 J. Vac. Sci. Technol. 6 388
Google Scholar
[13] Qiu M J, Zhai L, Cui J C, Fu B Q, Li M, Hou Q 2018 Chin. Phys. B 27 073103
Google Scholar
[14] Liu Y L, Zhang Y, Luo G N, Lu G H 2009 J. Nucl. Mater. 390/391 1032
Google Scholar
[15] Jiang B, Wan F R, Geng W T 2010 Phys. Rev. B 81 134112
[16] Liu Y L, Gao A Y, Lu W, Zhou H B, Zhang Y 2012 Chin. Phys. Lett. 29 077101
[17] Guo W, Ge L, Yuan Y, Cheng L, Wang S, Zhang X, Lu G H 2019 Nucl. Fusion 59 026005
Google Scholar
[18] Terentyev D, Dubinko V, Bakaev A, Zayachuk Y, van Renterghem W, Grigorev P 2014 Nucl. Fusion 54 042004
Google Scholar
[19] Zhou H B, Liu Y L, Jin S, Zhang Y, Luo G N, Lu G H 2010 Nucl. Fusion 50 025016
Google Scholar
[20] Wang X X, Niu L L, Wang S 2017 J. Nucl. Mater. 487 158
Google Scholar
[21] Fu B Q, Xu B, Lai W S, Yuan Y, Xu H Y, Li C, Jia Y Z, Liu W 2013 J. Nucl. Mater. 441 24
Google Scholar
[22] 王欣欣, 张颖, 周洪波, 王金龙 2014 63 046103
Google Scholar
Wang X X, Zhang Y, Zhou H B, Wang J L 2014 Acta Phys. Sin. 63 046103
Google Scholar
[23] 汪俊, 张宝玲, 周宇璐, 侯氢 2011 60 106601
Google Scholar
Wang J, Zhang B L, Zhou Y L, Hou Q 2011 Acta Phys. Sin. 60 106601
Google Scholar
[24] 严六明, 朱素华 2013 分子动力学模拟的理论与实践 (北京: 科学出版社) 第6−12页
Yan L M, Zhu S H 2013 Theory and Practice of Molecular Dynamics Simulation (Beijing: Science Press) pp6−12 (in Chinese)
[25] Hou Q, Li M, Zhou Y, Cui J, Cui Z, Wang J 2013 Comput. Phys. Commun. 184 2091
Google Scholar
[26] Fu B Q, Qiu M J, Cui J C, Li M, Hou Q 2018 J. Nucl. Mater. 508 278
Google Scholar
[27] Fu B Q, Qiu M J, Cui J C, Li M, Wang J, Hou Q 2019 Nucl. Instrum. Meth. B 452 21
Google Scholar
[28] Zhou Y L, Wang J, Hou Q, Deng A H 2014 J. Nucl. Mater. 446 49
Google Scholar
[29] Chandrasekhar S 1943 Rev. Mod. Phys. 15 1
Google Scholar
[30] Fernandez N, Ferro Y, Kato D 2015 Acta Mater. 94 307
Google Scholar
[31] Ahlgren T, Bukonte L 2016 J. Nucl. Mater. 479 195
Google Scholar
[32] Bonny G, Grigorev P, Terentyev D 2014 J. Phys.-Condens. Mat. 26 485001
Google Scholar
[33] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[34] Fu B Q, Liu W, Li Z L 2009 Appl. Surf. Sci. 255 8511
Google Scholar
[35] Marinica M C, Ventelon L, Gilbert M R, Proville L, Dudarev S L, Marian J, Bencteux G, Willaime F 2013 J. Phys.-Condens. Mat. 25 395502
Google Scholar
[36] Stukowski A 2010 Model. Simul. Mater. Sci. 18 015012
Google Scholar
[37] Cheng G J, Fu B Q, Hou Q, Zhou X S, Wang J 2016 Chinese Phys. B 25 076602
Google Scholar
[38] Fu B Q, Fitzgerald S P, Hou Q, Wang J, Li M 2017 Nucl. Instrum. Meth. B 393 169
Google Scholar
-
图 1 含有空位-H复合体(VH2)的初始超胞, 其中红色点表示W原子, 蓝色球表示H原子
Fig. 1. One simulation box with vacancy-H complex (VH2), where red pots represent W atoms and blue spheres represent H atoms.
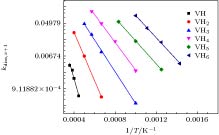
图 2 不同温度下, 空位-H复合体(VHx+1)的含量(
${y_{{\rm{V}}{{\rm{H}}_{x + 1}}}}\left( t \right) = {{{N_{{\rm{V}}{{\rm{H}}_{x + 1}}}}\left( t \right)} / {{N_{\rm{b}}}}}$ )与时间(t)的变化, 其中曲线由 (10)式拟合Fig. 2. Ratio of VHx+1 in the simulation (
${y_{{\rm{V}}{{\rm{H}}_{x + 1}}}}\left( t \right) = {{{N_{{\rm{V}}{{\rm{H}}_{x + 1}}}}\left( t \right)} / {{N_{\rm{b}}}}}$ ) as function of time (t), where the curves are fitted by Eq. (10).
图 3 不同空位-H复合体(VHx+1)的H解离系数(kdiss, x+1)与温度(T)的变化, 其中曲线由公式lnk = lnν – E/kB/T拟合
Fig. 3. Dissociation coefficients (kdiss, x+1) of H detrapping from various VHx+1 complex as functions of temperature (T), where the curves are fitted by equation lnk = lnν – E/kB/T.
-
[1] Lu G H, Zhou H B, Becquart C S 2014 Nucl. Fusion 54 086001
Google Scholar
[2] 李建刚, 宋云涛, 刘永, 汪小琳, 万元熙 2016 聚变工程试验堆装置主机设计 (北京: 科学出版社) 第250−252页
Li J G, Song Y T, Liu Y, Wang X L, Wan Y X 2016 Main Machine Design of Fusion Engineering Test Reactor (Beijing: Science Press) pp250−252 (in Chinese)
[3] Jia Y Z, Liu W, Xu B, Luo G N, Li C, Fu B Q, de Temmerman G 2015 J. Nucl. Mater. 463 312
Google Scholar
[4] Yi X, Jenkins M L, Hattar K, Edmondson P D, Roberts S G 2015 Acta Mater. 92 163
Google Scholar
[5] Hu X, Koyanagi T, Fukuda M, Kumar N A P K, Snead L L, Wirth B D, Katoh Y 2016 J. Nucl. Mater. 480 235
Google Scholar
[6] Fu B Q, Lai W S, Yuan Y, Xu H Y, Li C, Jia Y Z, Liu W 2013 Chinese Phys. B 22 126601
Google Scholar
[7] Ye M Y 2005 Plasma Sci. Technol. 7 2828
Google Scholar
[8] Fu B Q, Qiu M J, Zhai L, Yang A L, Hou Q 2019 Nucl. Instrum. Meth. B 450 220
Google Scholar
[9] Oyaidzu M, Hayashi T, Alimov V K 2016 Nucl. Mater. Energy 9 93
Google Scholar
[10] Jia Y Z, Liu W, Xu B, Qu S L, Shi L Q, Morgan T W 2017 Nucl. Fusion 57 034003
Google Scholar
[11] Heinola K, Ahlgren T 2010 Phys. Rev. B 81 073409
Google Scholar
[12] Frauenfelder R 1969 J. Vac. Sci. Technol. 6 388
Google Scholar
[13] Qiu M J, Zhai L, Cui J C, Fu B Q, Li M, Hou Q 2018 Chin. Phys. B 27 073103
Google Scholar
[14] Liu Y L, Zhang Y, Luo G N, Lu G H 2009 J. Nucl. Mater. 390/391 1032
Google Scholar
[15] Jiang B, Wan F R, Geng W T 2010 Phys. Rev. B 81 134112
[16] Liu Y L, Gao A Y, Lu W, Zhou H B, Zhang Y 2012 Chin. Phys. Lett. 29 077101
[17] Guo W, Ge L, Yuan Y, Cheng L, Wang S, Zhang X, Lu G H 2019 Nucl. Fusion 59 026005
Google Scholar
[18] Terentyev D, Dubinko V, Bakaev A, Zayachuk Y, van Renterghem W, Grigorev P 2014 Nucl. Fusion 54 042004
Google Scholar
[19] Zhou H B, Liu Y L, Jin S, Zhang Y, Luo G N, Lu G H 2010 Nucl. Fusion 50 025016
Google Scholar
[20] Wang X X, Niu L L, Wang S 2017 J. Nucl. Mater. 487 158
Google Scholar
[21] Fu B Q, Xu B, Lai W S, Yuan Y, Xu H Y, Li C, Jia Y Z, Liu W 2013 J. Nucl. Mater. 441 24
Google Scholar
[22] 王欣欣, 张颖, 周洪波, 王金龙 2014 63 046103
Google Scholar
Wang X X, Zhang Y, Zhou H B, Wang J L 2014 Acta Phys. Sin. 63 046103
Google Scholar
[23] 汪俊, 张宝玲, 周宇璐, 侯氢 2011 60 106601
Google Scholar
Wang J, Zhang B L, Zhou Y L, Hou Q 2011 Acta Phys. Sin. 60 106601
Google Scholar
[24] 严六明, 朱素华 2013 分子动力学模拟的理论与实践 (北京: 科学出版社) 第6−12页
Yan L M, Zhu S H 2013 Theory and Practice of Molecular Dynamics Simulation (Beijing: Science Press) pp6−12 (in Chinese)
[25] Hou Q, Li M, Zhou Y, Cui J, Cui Z, Wang J 2013 Comput. Phys. Commun. 184 2091
Google Scholar
[26] Fu B Q, Qiu M J, Cui J C, Li M, Hou Q 2018 J. Nucl. Mater. 508 278
Google Scholar
[27] Fu B Q, Qiu M J, Cui J C, Li M, Wang J, Hou Q 2019 Nucl. Instrum. Meth. B 452 21
Google Scholar
[28] Zhou Y L, Wang J, Hou Q, Deng A H 2014 J. Nucl. Mater. 446 49
Google Scholar
[29] Chandrasekhar S 1943 Rev. Mod. Phys. 15 1
Google Scholar
[30] Fernandez N, Ferro Y, Kato D 2015 Acta Mater. 94 307
Google Scholar
[31] Ahlgren T, Bukonte L 2016 J. Nucl. Mater. 479 195
Google Scholar
[32] Bonny G, Grigorev P, Terentyev D 2014 J. Phys.-Condens. Mat. 26 485001
Google Scholar
[33] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637
Google Scholar
[34] Fu B Q, Liu W, Li Z L 2009 Appl. Surf. Sci. 255 8511
Google Scholar
[35] Marinica M C, Ventelon L, Gilbert M R, Proville L, Dudarev S L, Marian J, Bencteux G, Willaime F 2013 J. Phys.-Condens. Mat. 25 395502
Google Scholar
[36] Stukowski A 2010 Model. Simul. Mater. Sci. 18 015012
Google Scholar
[37] Cheng G J, Fu B Q, Hou Q, Zhou X S, Wang J 2016 Chinese Phys. B 25 076602
Google Scholar
[38] Fu B Q, Fitzgerald S P, Hou Q, Wang J, Li M 2017 Nucl. Instrum. Meth. B 393 169
Google Scholar
下载:
计量
- 文章访问数: 8380
- PDF下载量: 119
- 被引次数: 0
