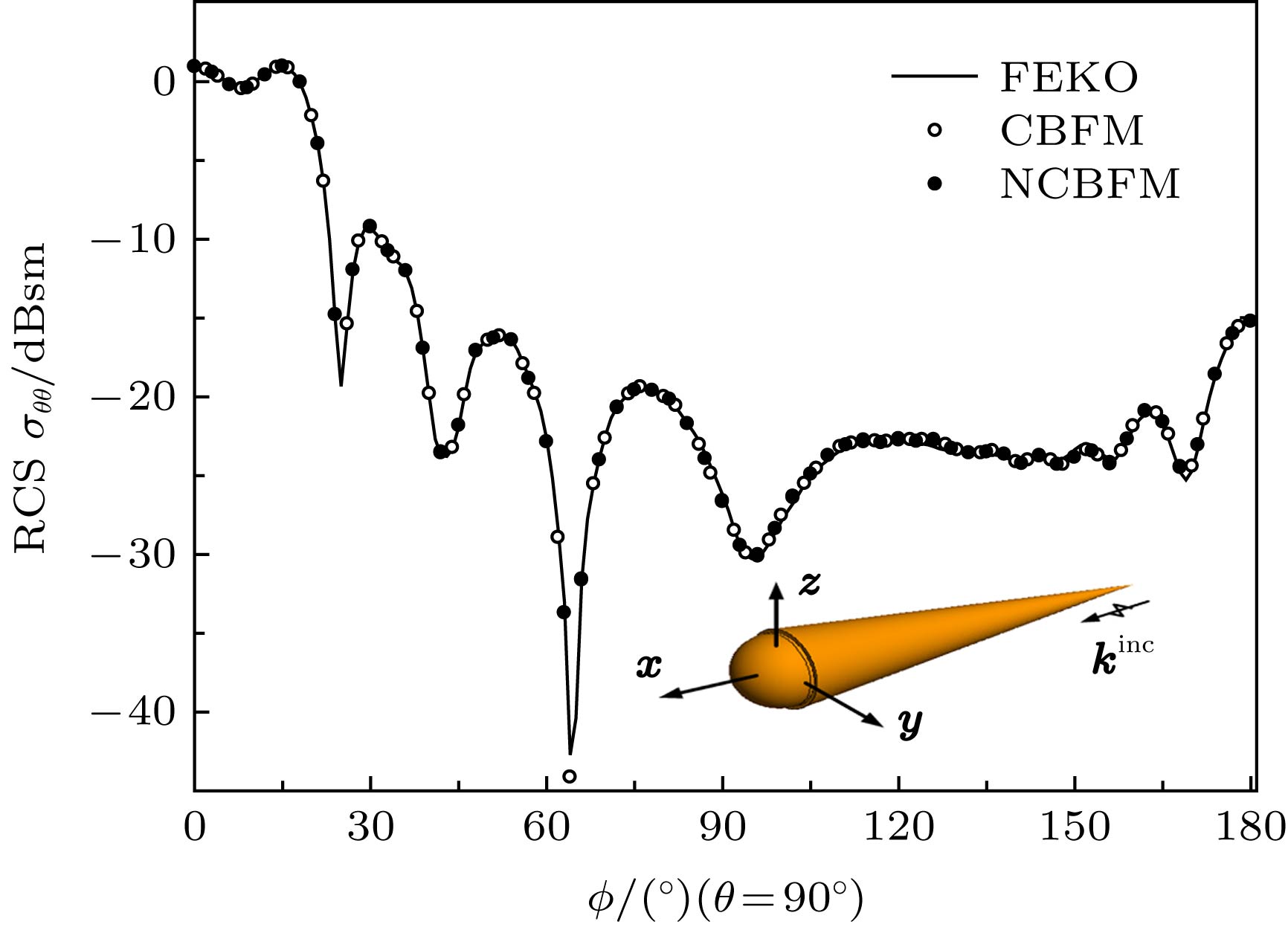
-
针对特征基函数法在分析电大目标电磁散射特性时存在缩减矩阵方程迭代求解收敛慢的问题, 提出一种新型缩减矩阵构造方法提高特征基函数法的迭代求解效率. 首先, 应用奇异值分解技术压缩激励源, 求解出新激励源下各子域的特征基函数; 其次, 将新激励源和特征基函数作为构造缩减矩阵的检验函数和基函数, 新方法构造的缩减矩阵的对角子矩阵均为单位矩阵, 缩减矩阵条件数得到了优化. 与传统方法相比, 新方法构造的缩减矩阵方程迭代求解效率得到了显著提高; 另外, 由于矩阵方程求解次数减少, 特征基函数的构造效率也得到了提高, 数值结果证明了新方法的精确性和有效性.The characteristic basis function method is known as an effective method to solve the electromagnetic scattering problems, but the convergence of the iterative solution of the reduced matrix equation is slow when the characteristic basis function method is used to analyze the electromagnetic scattering characteristics of the electrically large target. In order to mitigate this problem, a new reduced matrix construction method is proposed to improve the iterative solution efficiency of characteristic basis function method in this paper. Firstly, the singular value decomposition technique is used to compress the incident excitations, and the characteristic basis functions of each sub-domain under the new excitations are solved. Then, the new excitations and the characteristic basis functions are defied as the testing and basis functions to construct the reduced matrix. The diagonal sub-matrices of the reduced matrix constructed by the new testing and basis functions are all identity matrices, thereby improving the condition of reduced matrix. Thus, the total number of iterations to achieve reasonable results is significantly reduced. Numerical simulations are conducted to validate the performance of the proposed method. The results demonstrate that the efficiency of the iterative solution of the reduced matrix equation constructed by the new method is significantly improved. Furthermore, the characteristic basis functions’ generation time required by the proposed method is noticeably less than that by the traditional characteristic basis function method due to the reduced number of matrix equation solutions.
-
Keywords:
- characteristic basis function method /
- reduced matrix /
- singular value decomposition /
- characteristic basis functions
[1] Harrington R F 1993 Field Computation by Moment Methods (New York: Wiley-IEEE Press) pp5−7
[2] Coifman R, Rokhlin V, Wandzura S 1993 IEEE Antennas Propagat. Mag. 35 7
[3] Song J M, Lu C C, Chew W C 1997 IEEE Trans. Antenn. Propag. 45 1488
Google Scholar
[4] 王晓冰, 梁子长, 吴振森 2012 61 124104
Google Scholar
Wang X B, Liang Z C, Wu Z S 2012 Acta Phys. Sin. 61 124104
Google Scholar
[5] Ma J, Guo L X, Wang A Q 2009 Chin. Phys. B 18 3431
Google Scholar
[6] Nie X C, Yuan N, Li L W 2008 IEEE Trans. Antenn. Propag. 56 3526
Google Scholar
[7] Lu W B, Cui T J, Zhao H 2007 IEEE Trans. Antenn. Propag. 55 414
Google Scholar
[8] Freni A, Vita D P, Pirinoli P, Matekovits L, Vecchi G 2011 IEEE Trans. Antenn. Propag. 59 4588
Google Scholar
[9] Suter E, Mosing J R 2000 Microw. Opt. Technol. Lett. 26 270
Google Scholar
[10] Guan L, He Z, Ding D Z, Chen R S 2019 IEEE Trans. Antenn. Propag. 67 199
Google Scholar
[11] Chen Y, Wang C F 2015 IEEE Trans. Antenn. Propag. 63 1004
Google Scholar
[12] Prakash V V S, Mittra R 2003 Microw. Opt. Technol. Lett. 36 95
Google Scholar
[13] Sun Y F, Chan C H, Mittra R 2003 IEEE Antennas and Propagation Society International Symposium Columbus, June 22−27, 2003 p1068
[14] Lucente E, Monorchio A, Mittra R 2008 IEEE Trans. Antenn. Propag. 56 999
Google Scholar
[15] 侯兆国, 王超, 董纯柱, 殷红成 2011 系统工程与电子技术 33 1458
Google Scholar
Hou Z G, Wang C, Dong C Z, Yin H C 2011 Syst. Engineer. Electron. 33 1458
Google Scholar
[16] Ding J, Li J F, Zhang T 2016 IEICE Electron. Expr. 13 1
[17] Zhu J Y, Sun Y F, Fang H Y 2018 Prog. Electromag. Res. M 68 173
Google Scholar
[18] Tanaka T, Inasawa Y, Yoneda N, Miyashita H 2018 IEICE Trans. Electron. E101.C 96
[19] 王仲根, 唐晓菀, 汪强 2018 电子与信息学报 40 573
Google Scholar
Wang Z G, Tang X W, Wang Q 2018 J. Electron. Inf. Tech. 40 573
Google Scholar
[20] Fenni I, Roussel H, Darces M 2016 IEEE Trans. Antenn. Propag. 64 4539
Google Scholar
[21] 王仲根, 孙玉发, 王国华 2013 62 204102
Google Scholar
Wang Z G, Sun Y F, Wang G H 2013 Acta Phys. Sin. 62 204102
Google Scholar
[22] Fang X X, Cao Q S, Zhou Y 2019 IEEE Trans. Electromagn. Compat. 61 191
Google Scholar
[23] Chen X L, Niu Z Y, Li Z Gu C Q 2011 J. Electromagn. Waves Appl. 25 1940
Google Scholar
[24] Garcia E, Delgado C, Diego I G, Catedra M F 2008 IEEE Trans. Antenn. Propag. 56 2363
Google Scholar
[25] Hu J, Lu W, Shao H, Nie Z 2012 IEEE Trans. Antenn. Propag. 60 5709
Google Scholar
[26] Hu L, Li W L, Mittra R 2010 IEEE Trans. Antenn. Propag. 58 3086
Google Scholar
[27] García E, Delgado C, Cátedra F 2019 IEEE Trans. Antenn. Propag. 67 3241
Google Scholar
[28] Woo A C, Wang H T G, Schuh M J 1993 IEEE Antennas Propagat. Mag. 35 84
Google Scholar
-
图 1 (a)不同SVD门限下2种方法的计算误差及CBFs数目; (b)左半球面4个子域的奇异值分布曲线; (c)导体球双站RCS
Fig. 1. (a) Calculation error and numbers of CBFs under different SVD thresholds of two methods; (b) singular value distribution curve in four sub-domains of the left hemisphere; (c) bistatic RCS of PEC sphere.
表 1 计算时间比较
Table 1. Comparison of computation time.
目标及未知量个数 方法 阻抗矩阵填充/s 基函数构造/s 缩减矩阵构造/s 缩减矩阵方程求解/s 计算时间/s 导体球(17278) CBFM 239.9 1081.4 41.7 0.44 1375.6 NCBFM 239.1 979.4 40.8 0.31 1267.9 锥球带缝体(124685) CBFM 3297.5 27736.4 1535.7 104.5 32740.1 NCBFM 3289.2 26985.1 1506.6 57.3 31889.7 杏仁体(153690) CBFM 4097.8 33173.5 3553.7 237.8 83936.8 NCBFM 4098.4 31832.3 3524.1 121.2 61437.9 
下载: 导出CSV
-
[1] Harrington R F 1993 Field Computation by Moment Methods (New York: Wiley-IEEE Press) pp5−7
[2] Coifman R, Rokhlin V, Wandzura S 1993 IEEE Antennas Propagat. Mag. 35 7
[3] Song J M, Lu C C, Chew W C 1997 IEEE Trans. Antenn. Propag. 45 1488
Google Scholar
[4] 王晓冰, 梁子长, 吴振森 2012 61 124104
Google Scholar
Wang X B, Liang Z C, Wu Z S 2012 Acta Phys. Sin. 61 124104
Google Scholar
[5] Ma J, Guo L X, Wang A Q 2009 Chin. Phys. B 18 3431
Google Scholar
[6] Nie X C, Yuan N, Li L W 2008 IEEE Trans. Antenn. Propag. 56 3526
Google Scholar
[7] Lu W B, Cui T J, Zhao H 2007 IEEE Trans. Antenn. Propag. 55 414
Google Scholar
[8] Freni A, Vita D P, Pirinoli P, Matekovits L, Vecchi G 2011 IEEE Trans. Antenn. Propag. 59 4588
Google Scholar
[9] Suter E, Mosing J R 2000 Microw. Opt. Technol. Lett. 26 270
Google Scholar
[10] Guan L, He Z, Ding D Z, Chen R S 2019 IEEE Trans. Antenn. Propag. 67 199
Google Scholar
[11] Chen Y, Wang C F 2015 IEEE Trans. Antenn. Propag. 63 1004
Google Scholar
[12] Prakash V V S, Mittra R 2003 Microw. Opt. Technol. Lett. 36 95
Google Scholar
[13] Sun Y F, Chan C H, Mittra R 2003 IEEE Antennas and Propagation Society International Symposium Columbus, June 22−27, 2003 p1068
[14] Lucente E, Monorchio A, Mittra R 2008 IEEE Trans. Antenn. Propag. 56 999
Google Scholar
[15] 侯兆国, 王超, 董纯柱, 殷红成 2011 系统工程与电子技术 33 1458
Google Scholar
Hou Z G, Wang C, Dong C Z, Yin H C 2011 Syst. Engineer. Electron. 33 1458
Google Scholar
[16] Ding J, Li J F, Zhang T 2016 IEICE Electron. Expr. 13 1
[17] Zhu J Y, Sun Y F, Fang H Y 2018 Prog. Electromag. Res. M 68 173
Google Scholar
[18] Tanaka T, Inasawa Y, Yoneda N, Miyashita H 2018 IEICE Trans. Electron. E101.C 96
[19] 王仲根, 唐晓菀, 汪强 2018 电子与信息学报 40 573
Google Scholar
Wang Z G, Tang X W, Wang Q 2018 J. Electron. Inf. Tech. 40 573
Google Scholar
[20] Fenni I, Roussel H, Darces M 2016 IEEE Trans. Antenn. Propag. 64 4539
Google Scholar
[21] 王仲根, 孙玉发, 王国华 2013 62 204102
Google Scholar
Wang Z G, Sun Y F, Wang G H 2013 Acta Phys. Sin. 62 204102
Google Scholar
[22] Fang X X, Cao Q S, Zhou Y 2019 IEEE Trans. Electromagn. Compat. 61 191
Google Scholar
[23] Chen X L, Niu Z Y, Li Z Gu C Q 2011 J. Electromagn. Waves Appl. 25 1940
Google Scholar
[24] Garcia E, Delgado C, Diego I G, Catedra M F 2008 IEEE Trans. Antenn. Propag. 56 2363
Google Scholar
[25] Hu J, Lu W, Shao H, Nie Z 2012 IEEE Trans. Antenn. Propag. 60 5709
Google Scholar
[26] Hu L, Li W L, Mittra R 2010 IEEE Trans. Antenn. Propag. 58 3086
Google Scholar
[27] García E, Delgado C, Cátedra F 2019 IEEE Trans. Antenn. Propag. 67 3241
Google Scholar
[28] Woo A C, Wang H T G, Schuh M J 1993 IEEE Antennas Propagat. Mag. 35 84
Google Scholar
下载:
计量
- 文章访问数: 7860
- PDF下载量: 38
- 被引次数: 0
